当前位置： 首页 > news >正文

ZeroTier客户端连接服务器

news 2026/2/11 5:06:11

ZeroTier客户端连接服务器

  1. 下载客户端 https://www.zerotier.com/download/
  2. 加入新的网络（例如d5e04297a16fa690，由管理员提供）
  3. 管理员授权并告知服务器IP
  4. 测试连接：ping 服务器IP
  5. 使用putty, pycharm, vscode等工具连接即可

官方文档 https://docs.zerotier.com/getting-started/getting-started

注: 若路由器无法获取IPv4的物理IP，可尝试打开路由器IPv6功能。

相关文章：

ZeroTier客户端连接服务器

ZeroTier客户端连接服务器 下载客户端 https://www.zerotier.com/download/加入新的网络（例如d5e04297a16fa690，由管理员提供）管理员授权并告知服务器IP测试连接：ping 服务器IP使用putty, pycharm, vscode等工具连接即可 官方文…...

编程日记 2023/9/9 4:30:14

NFT Insider#106：The Sandbox 与 Light Matrix 以及鲁比尼拳击场达成战略合作

引言：NFT Insider由NFT收藏组织WHALE Members、BeepCrypto联合出品，浓缩每周NFT新闻，为大家带来关于NFT最全面、最新鲜、最有价值的讯息。每期周报将从NFT市场数据，艺术新闻类，游戏新闻类，虚拟世界类&#…...

编程日记 2023/9/9 4:29:11

【猿灰灰赠书活动 - 04期】- 【分布式统一大数据虚拟文件系统——Alluxio原理、技术与实践】

👨‍💻本文专栏：赠书活动专栏（为大家争取的福利，免费送书） 👨‍💻本文简述：博文为大家争取福利，与机械工业出版社合作进行送书活动 👨‍&#x1f…...

编程日记 2023/9/9 4:28:09

前端element表格导出excel

一&#xff1a;安装依赖 npm install xlsx file-saver --save二&#xff1a;在组件中导入 import FileSaver from file-saver import XLSX from xlsx三&#xff1a;给对应表格添加id&#xff0c;绑定方法 <el-table idtableDom> <el-button click"exportExc…...

编程日记 2023/9/9 4:27:08

React中的类组件和函数组件（详解）

React的核心思想就是组件化&#xff0c;相对于Vue来说&#xff0c;React的组件化更加灵活和多样。主要可以分为两大类&#xff1a;函数组件&#xff0c;类组件&#xff0c;这两大类组件的名称必须是大写字母开头 一、函数组件 函数组件通常是function进行定义的函数&#xff0…...

编程日记 2023/9/9 4:26:07

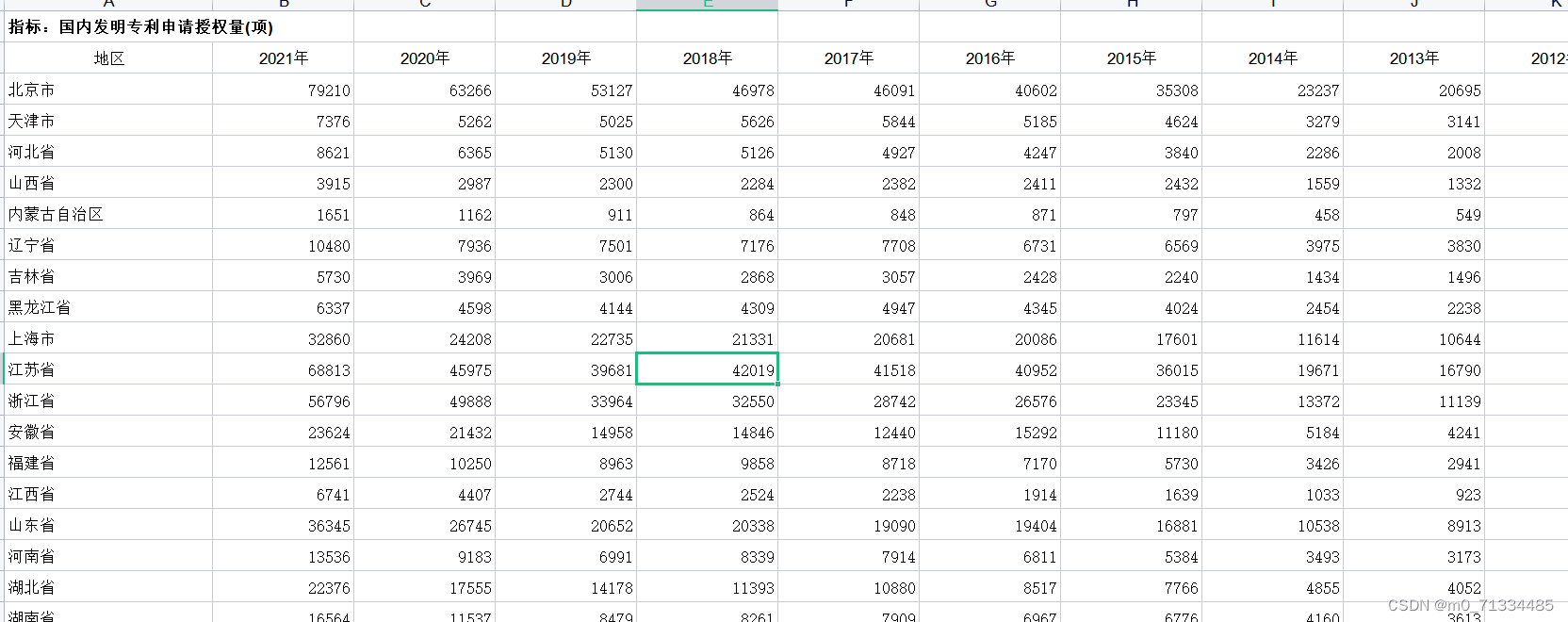
1987-2021年全国31省专利申请数和授权数

1987-2021年全国31省国内三种专利申请数和授权数 1、时间&#xff1a;1987-2021年 2、来源&#xff1a;整理自国家统计局、科技统计年鉴、各省年鉴 3、范围&#xff1a;31省市 4、指标&#xff1a;国内专利申请受理量、国内发明专利申请受理量、国内实用新型专利申请受理量…...

编程日记 2023/9/9 4:25:05

欧洲云巨头OVHcloud收购边缘计算专家 gridscale

边缘计算社区近日获悉&#xff0c;欧洲云巨头OVHcloud已进入全面收购德国公司 gridscale 的谈判&#xff0c;该公司是一家专门从事超融合基础设施的软件提供商。 此次战略收购将标志着 OVHcloud 的另一个重要里程碑&#xff0c;使该集团能够显着加速其地理部署&#xff0c;并进…...

编程日记 2023/9/9 4:24:04

java从入门到起飞（八）——循环和递归

文章目录 Java循环1. 什么是循环&#xff1f;1.1 为什么需要循环&#xff1f;1.2 循环的分类 2. Java中的循环结构2.1 for循环2.2 while循环2.3 do-while循环 3. 循环控制语句3.1 break语句3.2 continue语句 4. 总结 Java递归1. 什么是递归2. 递归的原理3. 递归的实现4. 递归的…...

编程日记 2023/9/9 4:23:03

架构师成长之路|Redis实现延迟队列的三种方式

延迟队列实现 基于监听key过期实现的延迟队列实现，这里需要继承KeyspaceEventMessageListener类来实现监听redis键过期 public class KeyExpirationEventMessageListener extends KeyspaceEventMessageListener implementsApplicationEventPublisherAware {private static f…...

编程日记 2023/9/9 4:22:00

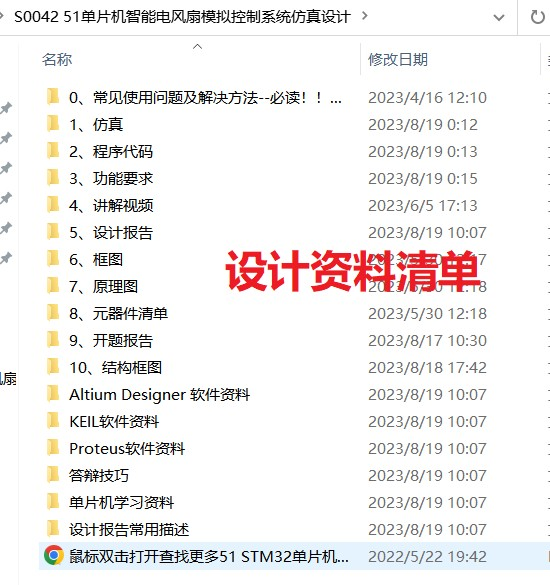
51单片机智能电风扇控制系统proteus仿真设计( 仿真+程序+原理图+报告+讲解视频）

51单片机智能电风扇控制系统仿真设计( proteus仿真程序原理图报告讲解视频&#xff09; 讲解视频1.主要功能&#xff1a;2.仿真3. 原理图4. 程序代码5.设计报告6. 设计资料内容清单 51单片机智能电风扇控制系统仿真设计( proteus仿真程序原理图报告讲解视频&#xff09; 仿真图…...

编程日记 2023/9/9 4:20:59

【设计模式】Head First 设计模式——工厂方法模式 C++实现

设计模式最大的作用就是在变化和稳定中间寻找隔离点&#xff0c;然后分离它们&#xff0c;从而管理变化。将变化像小兔子一样关到笼子里&#xff0c;让它在笼子里随便跳&#xff0c;而不至于跳出来把你整个房间给污染掉。 设计思想 定义一个用于创建对象的接口&#xff0c;让子…...

编程日记 2023/9/9 4:19:58

【爬虫】7.2. JavaScript动态渲染界面爬取-Selenium实战

JavaScript动态渲染界面爬取-Selenium实战 爬取的网页为&#xff1a;https://spa2.scrape.center&#xff0c;里面的内容都是通过Ajax渲染出来的&#xff0c;在分析xhr时候发现url里面有token参数&#xff0c;所有我们使用selenium自动化工具来爬取JavaScript渲染的界面。 fr…...

编程日记 2023/9/9 4:18:57

c语言实训心得3篇集合

c语言实训心得体会一&#xff1a; 在这个星期里&#xff0c;我们专业的学生在专业老师的带领下进行了c语言程序实践学习。在这之前&#xff0c;我们已经对c语言这门课程学习了一个学期&#xff0c;对其有了一定的了解&#xff0c;但是也仅仅是停留在了解的范围&#xff0c;对里…...

编程日记 2023/9/9 4:17:57

2023高教社杯数学建模B题思路代码 - 多波束测线问题

# 1 赛题 B 题 多波束测线问题 单波束测深是利用声波在水中的传播特性来测量水体深度的技术。声波在均匀介质中作匀 速直线传播&#xff0c; 在不同界面上产生反射&#xff0c; 利用这一原理&#xff0c;从测量船换能器垂直向海底发射声波信 号&#xff0c;并记录从声波发射到…...

编程日记 2023/9/9 4:16:56

MySql 变量

1.系统变量 1.1 系统变量分类 变量由系统定义&#xff0c;不是用户定义&#xff0c;属于 服务器 层面。系统变量分为全局系统变量&#xff08;需要添加 global 关键字&#xff09;以及会话系统变量&#xff08;需要添加 session 关键字&#xff09;&#xff0c;有时也把全局系…...

编程日记 2023/9/9 4:15:55

2023-简单点-make和build都是什么东西？

make make命令根据makefile.txt中的命令进行批量处理。 编译时自动检查文件是否更新&#xff0c;如果文件已经更改&#xff0c;make会对他重新编译&#xff0c;否则跳过。 编译选定的目标&#xff0c;但是Make只编译上次编译变化过的文件&#xff0c;减少重复劳动&#xff0…...

编程日记 2023/9/9 4:14:54

Nginx 学习（八）Nginx实现用IP测试灰度发布

1.1 问题 配置Nginx使其可以将动态访问转交给uWSGI&#xff1a; 1.2 方案 安装Python工具及依赖 安装uWSGI并编写配置文件 1.3 步骤 实现此案例需要按照如下步骤进行。 步骤一&#xff1a; 1)安装python依赖软件[rootproxy python]# yum -y install gcc make pytho…...

编程日记 2023/9/9 4:13:53

QT 自定义信号

自定义信号&#xff0c;需要 1.在singnals:区域下写信号函数&#xff0c;以及函数对应的参数 2. 需要emit关键字进行发射信号 3. 在需要处理该信号的其他类中&#xff0c;建立信号和其信号槽函数connect() 4. 在其他类中创建信号处理槽函数 #include "mythread.h"my…...

编程日记 2023/9/9 4:12:51

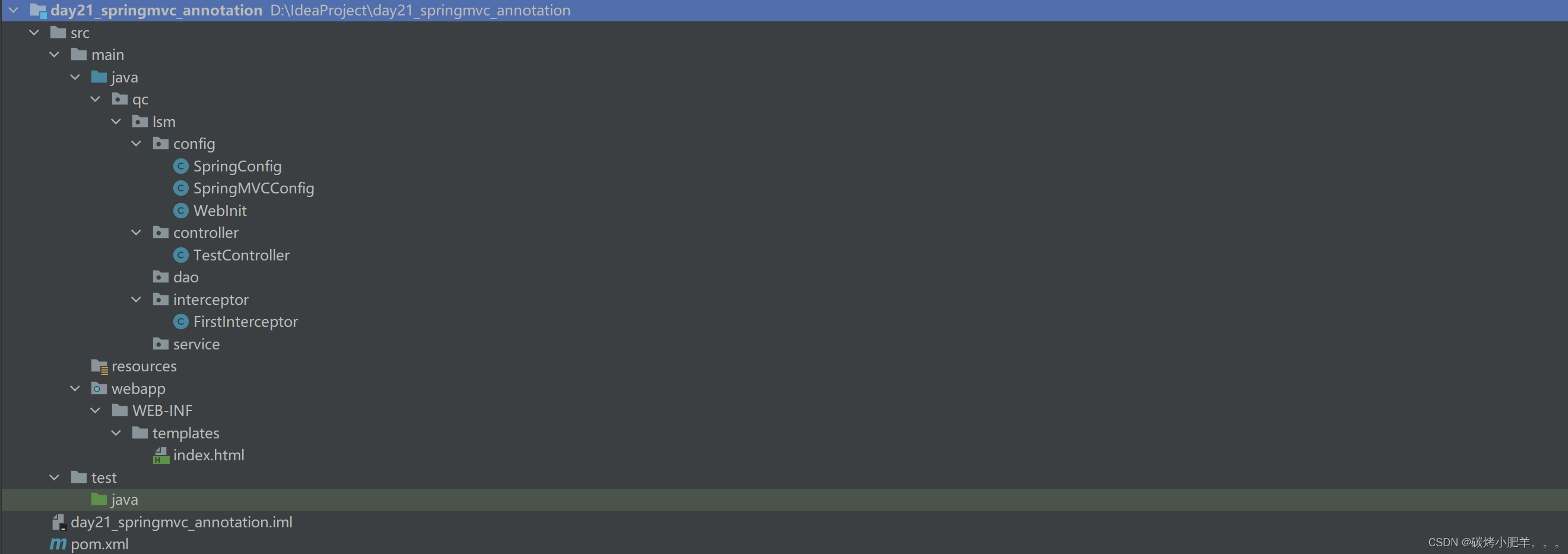
注解方式配置SpringMVC

注解配置SpringMVC 1. 初始化类&#xff0c;代替web.xml2. 创建SpringConfig配置类&#xff0c;代替spring的配置文件3. 创建SpringMVCConfig配置类&#xff0c;代替SpringMVC.xml配置文件4. 项目结构 1. 初始化类&#xff0c;代替web.xml Spring3.2引入了一个便利的WebApplic…...

编程日记 2023/9/9 4:11:50

2023年限售股解禁研究报告

第一章 概述 解禁是指限售流通股过了限售承诺期&#xff0c;可以在二级市场自由买卖的过程。根据流通性质&#xff0c;可将上市公司股份分为有限售条件的流通股&#xff08;“限售流通股”&#xff09;及无限售条件的流通股&#xff08;“流通股”&#xff09;。 限售流通股指…...

编程日记 2023/9/9 4:10:49

多云管理“拦路虎”：深入解析网络互联、身份同步与成本可视化的技术复杂度​

一、引言&#xff1a;多云环境的技术复杂性本质​​ 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时&#xff0c;​​基础设施的技术债呈现指数级积累​​。网络连接、身份认证、成本管理这三大核心挑战相互嵌套&#xff1a;跨云网络构建数据…...

编程新知 2026/2/11 0:21:49

谷歌浏览器插件

项目中有时候会用到插件 sync-cookie-extension1.0.0&#xff1a;开发环境同步测试 cookie 至 localhost&#xff0c;便于本地请求服务携带 cookie 参考地址&#xff1a;https://juejin.cn/post/7139354571712757767 里面有源码下载下来&#xff0c;加在到扩展即可使用FeHelp…...

编程新知 2025/8/16 3:55:30

【Linux】shell脚本忽略错误继续执行

在 shell 脚本中&#xff0c;可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行&#xff0c;可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令&#xff0c;并忽略错误 rm somefile…...

编程新知 2025/9/11 15:27:32

跨链模式：多链互操作架构与性能扩展方案

跨链模式&#xff1a;多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈&#xff1a;模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展&#xff08;H2Cross架构&#xff09;&#xff1a; 适配层&#xf…...

编程新知 2026/2/5 14:15:13

Cloudflare 从 Nginx 到 Pingora：性能、效率与安全的全面升级

在互联网的快速发展中&#xff0c;高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司&#xff0c;近期做出了一个重大技术决策&#xff1a;弃用长期使用的 Nginx&#xff0c;转而采用其内部开发…...

编程新知 2026/1/29 21:20:51

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南

1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发&#xff0c;使用DevEco Studio作为开发工具&#xff0c;采用Java语言实现&#xff0c;包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

编程新知 2025/12/19 22:56:05

Typeerror: cannot read properties of undefined (reading ‘XXX‘)

最近需要在离线机器上运行软件&#xff0c;所以得把软件用docker打包起来&#xff0c;大部分功能都没问题&#xff0c;出了一个奇怪的事情。同样的代码&#xff0c;在本机上用vscode可以运行起来&#xff0c;但是打包之后在docker里出现了问题。使用的是dialog组件&#xff0c;…...

编程新知 2025/9/24 3:05:06

算法笔记2

1.字符串拼接最好用StringBuilder&#xff0c;不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

编程新知 2026/1/27 12:17:05

#Uniapp篇：chrome调试unapp适配

chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器&#xff1a;Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

编程新知 2026/1/4 21:36:42

GitFlow 工作模式（详解）

今天再学项目的过程中遇到使用gitflow模式管理代码&#xff0c;因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存&#xff0c;无论是github还是gittee&#xff0c;都是一种基于git去保存代码的形式&#xff0c;这样保存代码…...

编程新知 2026/1/26 12:37:40