机器学习笔记之最优化理论与方法(七)无约束优化问题——常用求解方法(上)
机器学习笔记之最优化理论与方法——基于无约束优化问题的常用求解方法[上]
- 引言
- 总体介绍
- 回顾:线搜索下降算法
- 收敛速度的衡量方式
- 线性收敛范围
- 高阶收敛范围
- 二次终止性
- 朴素算法:坐标轴交替下降法
- 最速下降法(梯度下降法)
- 梯度下降法的特点
- 针对最速下降法缺陷代码示例
引言
本节将介绍无约束优化问题的常用求解方法,包括坐标轴交替下降法、最速下降法。
本节是对优化算法(十~十七)最速下降法(梯度下降法)的理论补充,其中可能出现一些定理的证明过程这里不再赘述,并在相应位置附加链接。
总体介绍
从本节开始,将介绍四大类无约束优化问题的常用求解方法:
- 坐标轴交替下降法;
- 最速下降法;
- 牛顿法;
- 拟牛顿法。
这些方法的核心区别在于:下降方向选择策略的差异性。通过介绍各算法选择下降方向的方式,并延伸至该算法的特点。
回顾:线搜索下降算法
关于最小化目标函数 min f ( x ) \min f(x) minf(x)的无约束优化问题,线搜索下降算法的迭代步骤表示如下:
- 给定数值解序列 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞的迭代初始点 x 0 ( k = 0 ) x_0(k=0) x0(k=0);
这仅是从数学角度对数值解序列进行描述。如果从算法角度,它不可能是一个长度为无穷大的序列。可以通过终止条件使迭代算法停止。 - 判断点 x k x_k xk是否满足终止条件:是,则终止;
- 寻找 x k x_k xk位置的下降方向 D k \mathcal D_k Dk;
- 选择合适的步长 α k ≥ 0 \alpha_k \geq 0 αk≥0,使得:
f ( x k + α k ⋅ D k ) < f ( x k ) f(x_k + \alpha_k \cdot \mathcal D_k) < f(x_k) f(xk+αk⋅Dk)<f(xk) - 令: x k + 1 = x k + α k ⋅ D k x_{k+1} = x_k + \alpha_k \cdot \mathcal D_k xk+1=xk+αk⋅Dk;并令 k = k + 1 k = k+1 k=k+1,转步骤 2 2 2。
其中:
- 常用终止条件: ∥ ∇ f ( x k ) ∥ ≤ ϵ \|\nabla f(x_k)\| \leq \epsilon ∥∇f(xk)∥≤ϵ
其中ϵ \epsilon ϵ是一个较小的正值。例如1 0 − 6 10^{-6} 10−6。如果满足该条件,意味着:x k x_k xk点处的梯度 ∇ f ( x k ) \nabla f(x_k) ∇f(xk)已经充分接近于 0 0 0。
- 步长选择方式:基于区间的直接搜索法;非精确搜索准则(五~七);
包括Armijo,Glodstein,Wolfe \text{Armijo,Glodstein,Wolfe} Armijo,Glodstein,Wolfe准则。因为仅仅让{ f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞收敛并不是其达到最优解的充要条件。详见线搜索方法(步长角度;非精确搜索) - 下降方向;
针对不同的下降方向选择方式,产生不同种类的算法。而我们更关心的是对应算法产生的数值解序列 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞是否能够收敛至最优解 x ∗ x^* x∗,如果能够收敛至最优解 x ∗ x^* x∗,需要关心它的收敛速度情况。
收敛速度的衡量方式
对应文章详见:优化算法(九)收敛速度的简单认识
线性收敛范围
假设数值解序列 { x k } k = 0 ∞ ⇒ x ∗ \{x_k\}_{k=0}^{\infty} \Rightarrow x^* {xk}k=0∞⇒x∗,如果存在极限:
很明显,关于 β \beta β的取值范围: β ∈ [ 0 , 1 ] \beta \in [0,1] β∈[0,1]。
其中当β = 1 \beta=1 β=1时,分母与分子之间的差异性可视作完全相同;换句话说,当k k k充分大时,两者之间的差距确实存在,但小到可以忽略不计。称这种收敛方式为次线性收敛。当0 < β < 1 0<\beta<1 0<β<1时,可以明显观察到分母与分子之间存在比值的大小关系;通过该比值β \beta β可以明显观察到迭代过程中呈线性的收敛效果。当β = 0 \beta = 0 β=0时,和β = 1 \beta = 1 β=1相反,当k k k充分大时,分母与分子之间的差距足够大,甚至分子与分母相比,小到可以忽略不计。
lim k ⇒ ∞ ∥ x k + 1 − x ∗ ∥ ∥ x k − x ∗ ∥ = β \mathop{\lim}\limits_{k \Rightarrow \infty} \frac{\|x_{k+1} - x^*\|}{\|x_k - x^*\|} = \beta k⇒∞lim∥xk−x∗∥∥xk+1−x∗∥=β
根据 β \beta β的不同取值,有:
- 当 0 < β < 1 0 < \beta < 1 0<β<1时,称数值解序列 { x k } \{x_k\} {xk}为线性收敛;
- 当 β = 0 \beta = 0 β=0时,则称数值解序列 { x k } \{x_k\} {xk}为超线性收敛。
示例:假设 β = 1 2 \begin{aligned}\beta = \frac{1}{2}\end{aligned} β=21,那么:
{ ∥ x k + 1 − x ∗ ∥ = 1 2 ∥ x k − x ∗ ∥ ∥ x k + 2 − x ∗ ∥ = 1 2 ∥ x k + 1 − x ∗ ∥ = 1 4 ∥ x k − x ∗ ∥ ⋮ \begin{cases} \begin{aligned} \|x_{k+1} -x^*\| & = \frac{1}{2} \|x_k - x^*\| \\ \|x_{k+2} - x^*\| & = \frac{1}{2} \|x_{k+1} - x^*\| = \frac{1}{4}\|x_k - x^*\| \\ \vdots \\ \end{aligned} \end{cases} ⎩ ⎨ ⎧∥xk+1−x∗∥∥xk+2−x∗∥⋮=21∥xk−x∗∥=21∥xk+1−x∗∥=41∥xk−x∗∥
可以明显观察到其呈线性的收敛效果。
高阶收敛范围
如果存在 p ≥ 1 p \geq 1 p≥1,有:
lim k ⇒ ∞ ∥ x k + 1 − x ∗ ∥ ∥ x k − x ∗ ∥ p = β < + ∞ \mathop{\lim}\limits_{k \Rightarrow \infty} \frac{\|x_{k+1} - x^*\|}{\|x_k - x^*\|^p} = \beta < +\infty k⇒∞lim∥xk−x∗∥p∥xk+1−x∗∥=β<+∞
则称 { x k } \{x_k\} {xk}为 p p p阶收敛。
牛顿法在适当条件下被证明是二阶收敛。可以想象,当p > 1 p>1 p>1时,相比于线性收敛范围,高阶收敛必然是更高级别的收敛速度。从而有如下表达:
当 p > 1 p > 1 p>1时, p p p阶收敛必然为超线性收敛,但反之不一定成立。
验证:当 p > 1 p > 1 p>1时,可以将上式拆解为如下形式:
lim k ⇒ ∞ ∥ x k + 1 − x ∗ ∥ ∥ x k − x ∗ ∥ p = lim k ⇒ ∞ ( ∥ x k + 1 − x ∗ ∥ ∥ x k − x ∗ ∥ ⋅ 1 ∥ x k − x ∗ ∥ p − 1 ) \mathop{\lim}\limits_{k \Rightarrow \infty} \frac{\|x_{k+1} - x^*\|}{\|x_k - x^*\|^p} = \mathop{\lim}\limits_{k \Rightarrow \infty} \left(\frac{\|x_{k+1} - x^*\|}{\|x_k - x^*\|} \cdot \frac{1}{\|x_k - x^*\|^{p-1}}\right) k⇒∞lim∥xk−x∗∥p∥xk+1−x∗∥=k⇒∞lim(∥xk−x∗∥∥xk+1−x∗∥⋅∥xk−x∗∥p−11)
- 其中第一项描述的是线性收敛范围;观察第二项: lim k ⇒ ∞ 1 ∥ x k − x ∗ ∥ p − 1 \begin{aligned}\lim_{k \Rightarrow \infty} \frac{1}{\|x_k - x^*\|^{p-1}}\end{aligned} k⇒∞lim∥xk−x∗∥p−11在 p > 1 p>1 p>1条件下,其结果是 + ∞ +\infty +∞。
- 如果需要 lim k ⇒ ∞ ∥ x k + 1 − x ∗ ∥ ∥ x k − x ∗ ∥ ⋅ ∞ = β < ∞ \begin{aligned}\mathop{\lim}\limits_{k \Rightarrow \infty} \frac{\|x_{k+1} - x^*\|}{\|x_k - x^*\|} \cdot \infty = \beta < \infty\end{aligned} k⇒∞lim∥xk−x∗∥∥xk+1−x∗∥⋅∞=β<∞,必然需要 lim k ⇒ ∞ ∥ x k + 1 − x ∗ ∥ ∥ x k − x ∗ ∥ = 0 \begin{aligned}\mathop{\lim}\limits_{k \Rightarrow \infty} \frac{\|x_{k+1} - x^*\|}{\|x_k - x^*\|} = 0\end{aligned} k⇒∞lim∥xk−x∗∥∥xk+1−x∗∥=0,即超线性收敛。
二次终止性
关于判断一个算法的优劣性,除去收敛速度这个评价标准外,优化问题本身也可以作为算法优劣性的评价标准。算法针对某类简单问题:
- 可能无法在有限迭代步骤内实现收敛;
- 可能会在有限迭代步骤内实现收敛,但计算代价过大;
这样的算法本身存在问题。相反,如何衡量简单问题的基准 ? ? ?通常将目标函数为凸二次函数作为基准:
矩阵 Q \mathcal Q Q至少是半正定矩阵。
f ( x ) = 1 2 x T Q x + C T x Q ≽ 0 f(x) = \frac{1}{2}x^T \mathcal Qx + \mathcal C^T x \quad \mathcal Q \succcurlyeq 0 f(x)=21xTQx+CTxQ≽0
如果针对上述问题在有限迭代步骤内接近最优解,我们称该算法具有二次终止性。
朴素算法:坐标轴交替下降法
其基本思想表示为:给定初始点 x 0 ∈ R n x_0 \in \mathbb R^n x0∈Rn,依次沿坐标轴 e 1 , e 2 , ⋯ , e n e_1,e_2,\cdots,e_n e1,e2,⋯,en进行搜素。
关于坐标轴交替下降法,它并不想在迭代步骤中花费代价计算下降方向,而是直接选择坐标轴方向作为下降方向。这与吉布斯采样方法的思想——坐标上升法如出一辙。
对应算法框架表示如下:
- 给定初始点 x 0 ; k = 0 ; x_0;k=0; x0;k=0;
- 依然判断 ∥ ∇ f ( x k ) ∥ ≤ ϵ \|\nabla f(x_k)\| \leq \epsilon ∥∇f(xk)∥≤ϵ:如果满足,终止;
- 记 y 0 = x k y_0 = x_k y0=xk,令:
{ y i = y i − 1 + α i ⋅ e i α i = arg min f ( y i − 1 + α ⋅ e i ) i = 1 , 2 , ⋯ , n \begin{cases} y_i = y_{i-1} + \alpha_i \cdot e_i \\ \alpha_i = \mathop{\arg\min} f(y_{i-1} + \alpha \cdot e_i) \quad i=1,2,\cdots,n \end{cases} {yi=yi−1+αi⋅eiαi=argminf(yi−1+α⋅ei)i=1,2,⋯,n
解释:实际上该步骤是一个 n n n次循环。这里的 y i ( i = 1 , 2 , ⋯ , n ) y_i(i=1,2,\cdots,n) yi(i=1,2,⋯,n)分别表示特征空间中的具体点。这里以二维特征 x k ∈ R 2 ⇒ ( e 1 , e 2 ) x_k \in \mathbb R^2 \Rightarrow (e_1,e_2) xk∈R2⇒(e1,e2)为例,使用图像描述该过程:- 初始状态下, y 0 = x k : ( x 1 ( k ) , x 2 ( k ) ) y_0 = x_k:(x_1^{(k)},x_2^{(k)}) y0=xk:(x1(k),x2(k));
- 在除去 e 1 e_1 e1外,其他维度固定的条件下,此时固定优化方向为 e 1 e_1 e1,在该方向上的最优步长 α 1 \alpha_1 α1可表示为关于步长变量 α \alpha α函数 ϕ ( α ) \phi(\alpha) ϕ(α)的最优解:
α 1 = arg min α ϕ ( α ) = arg min α f ( y 0 + α ⋅ e 1 ) \alpha_1 = \mathop{\arg\min}\limits_{\alpha} \phi(\alpha) = \mathop{\arg\min}\limits_{\alpha} f(y_0 + \alpha \cdot e_1) α1=αargminϕ(α)=αargminf(y0+α⋅e1) - 找到 α 1 \alpha_1 α1后,通过 y 1 = y 0 + α 1 ⋅ e 1 y_1 = y_0 + \alpha_1 \cdot e_1 y1=y0+α1⋅e1可以得到第一次循环结束后更新的位置;
- 同上,继续循环,寻找除去 e 2 e_2 e2外,其他维度固定的条件下,求出 e 2 e_2 e2方向上的最优步长 α 2 \alpha_2 α2,以此类推。直到 n n n个维度全部被遍历一次为止,得到 y n = x k + 1 y_n= x_{k+1} yn=xk+1。对应图像表示如下:
当然这里n = 2 n=2 n=2。

- 在得到 x k + 1 = y n x_{k+1} = y_n xk+1=yn后, k = k + 1 k = k+1 k=k+1,并步骤 2 2 2,直到满足条件为止。
该算法的优势在于:
- 不需要花费额外代价计算下降方向;
- 步骤 3 3 3的循环中, e i ∈ R ( i = 1 , 2 , ⋯ , n ) e_i \in \mathbb R(i=1,2,\cdots,n) ei∈R(i=1,2,⋯,n),因而计算上相对简单。
- 当目标函数 f ( x ) f(x) f(x)中的决策变量 x ∈ R n x \in \mathbb R^n x∈Rn,其各分量 x i ( i = 1 , 2 , ⋯ , n ) x_i(i=1,2,\cdots,n) xi(i=1,2,⋯,n)之间的交叉程度很小时,该算法框架会非常有效。
什么是交叉程度很小——可理解为各分量之间的关联关系较小,甚至是线性无关。例如各分量满足可分离函数:各分量各算各的~
min f ( x ) = min [ f 1 ( x 1 ) + f 2 ( x 2 ) + ⋯ + f n ( x n ) ] = ∑ i = 1 n min f 1 ( x 1 ) \begin{aligned} \min f(x) & = \min [f_1(x_1) + f_2(x_2)+\cdots + f_n(x_n)] \\ & = \sum_{i=1}^n \min f_1(x_1) \end{aligned} minf(x)=min[f1(x1)+f2(x2)+⋯+fn(xn)]=i=1∑nminf1(x1)
相反,该算法的劣势在于:对于一般问题,该算法得到的数值解序列 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞不一定收敛。
如果决策变量内各分量之间的关联性程度较高,其产生的结果并不容易收敛,吉布斯采样同样存在这种缺陷。
一种改进方法描述:将线搜索方法与坐标轴交替下降法交替使用从而使数值解序列收敛。具体改进步骤如下:
前面步骤并没有发生变化,在通过坐标轴交替下降法找到 x ˉ k \bar{x}_k xˉk后,能够确定: f ( x ˉ k ) ≤ f ( x k ) f(\bar{x}_k) \leq f(x_k) f(xˉk)≤f(xk),也就是说: x k ⇒ x ˉ k x_k \Rightarrow \bar{x}_k xk⇒xˉk的方向 D k \mathcal D_k Dk一定是下降方向。
-
给定初始点 x 0 ; k = 0 ; x_0;k=0; x0;k=0;
-
依然判断 ∥ ∇ f ( x k ) ∥ ≤ ϵ \|\nabla f(x_k)\| \leq \epsilon ∥∇f(xk)∥≤ϵ:如果满足,终止;
-
记 y 0 = x k y_0 = x_k y0=xk,令:
{ y i = y i − 1 + α i ⋅ e i α i = arg min f ( y i − 1 + α ⋅ e i ) i = 1 , 2 , ⋯ , n \begin{cases} y_i = y_{i-1} + \alpha_i \cdot e_i \\ \alpha_i = \mathop{\arg\min} f(y_{i-1} + \alpha \cdot e_i) \quad i=1,2,\cdots,n \end{cases} {yi=yi−1+αi⋅eiαi=argminf(yi−1+α⋅ei)i=1,2,⋯,n
从而得到 x ˉ k \bar{x}_{k} xˉk。 -
以 x ˉ k \bar{x}_k xˉk为起始点, D k : x k ⇒ x ˉ k \mathcal D_k:x_k \Rightarrow \bar{x}_k Dk:xk⇒xˉk为下降方向使用线搜索方法选择合适步长,从而得到新的更新结果 x k + 1 x_{k+1} xk+1;
依然是基于2 2 2维特征,对应示例图像表示如下。

-
得到 x k + 1 x_{k+1} xk+1后, k = k + 1 k=k+1 k=k+1,并返回步骤 2 2 2。
最速下降法(梯度下降法)
其基本思想表示为:在迭代过程中,选择 x k x_k xk处的负梯度方向作为搜索方向。即: D k = − ∇ f ( x k ) \mathcal D_k = - \nabla f(x_k) Dk=−∇f(xk)。
而负梯度方向也被称作最速下降方向。
- 从泰勒展开式的角度观察,根据线搜索方法(方向角度)的下降方向的推导过程可知:若判断 x k x_k xk处的某方向 D \mathcal D D是否为下降方向,只需判断:
[ ∇ f ( x k ) ] T D < 0 [\nabla f(x_k)]^T \mathcal D < 0 [∇f(xk)]TD<0
那么方向 D \mathcal D D就是 x k x_k xk位置的下降方向。当 D = − ∇ f ( x k ) \mathcal D = -\nabla f(x_k) D=−∇f(xk)时,能够使 [ ∇ f ( x k ) ] T D [\nabla f(x_k)]^T \mathcal D [∇f(xk)]TD达到最小值:
这里仅关注向量∇ f ( x k ) , D \nabla f(x_k),\mathcal D ∇f(xk),D的方向信息,因而设∥ ∇ f ( x k ) ∥ = ∥ D ∥ = 1 \|\nabla f(x_k)\| = \|\mathcal D\| = 1 ∥∇f(xk)∥=∥D∥=1。
[ ∇ f ( x k ) ] T D = ∥ ∇ f ( x k ) ∥ ⋅ ∥ D ∥ cos θ [\nabla f(x_k)]^T \mathcal D = \|\nabla f(x_k)\| \cdot \|\mathcal D\| \cos \theta [∇f(xk)]TD=∥∇f(xk)∥⋅∥D∥cosθ
其中 θ \theta θ表示向量 ∇ f ( x k ) , D \nabla f(x_k),\mathcal D ∇f(xk),D(不分先后)之间的夹角。当 D , ∇ f ( x k ) \mathcal D,\nabla f(x_k) D,∇f(xk)之间夹角为 π 2 \begin{aligned}\frac{\pi}{2}\end{aligned} 2π时,能够取到 cos θ \cos \theta cosθ的最小值 − 1 -1 −1。 - 如果从方向导数的角度观察: [ ∇ f ( x k ) ] T D [\nabla f(x_k)]^T \mathcal D [∇f(xk)]TD,它可以看作: x k x_k xk所在位置处关于 D \mathcal D D的方向导数。在凸函数铺垫:梯度与方向导数中介绍过,对应方向导数可表示为:
这里示例x k x_k xk是二维特征,坐标为( x , y ) (x,y) (x,y)。
∂ Z ∂ D ∣ ( x , y ) = f x ( x k ) ⋅ cos α + f y ( x k ) ⋅ cos β = [ f x ( x k ) , f y ( x k ) ] ⏟ [ ∇ f ( x k ) ] T ( cos α cos β ) = [ ∇ f ( x k ) ] T D \begin{aligned} \frac{\partial \mathcal Z}{\partial \mathcal D}\mid_{(x,y)} & = f_x(x_k) \cdot \cos \alpha + f_y(x_k) \cdot \cos \beta \\ & = \underbrace{[f_x(x_k),f_y(x_k)]}_{[\nabla f(x_k)]^T} \begin{pmatrix} \cos \alpha \\ \cos \beta \end{pmatrix} \\ & = [\nabla f(x_k)]^T \mathcal D \end{aligned} ∂D∂Z∣(x,y)=fx(xk)⋅cosα+fy(xk)⋅cosβ=[∇f(xk)]T [fx(xk),fy(xk)](cosαcosβ)=[∇f(xk)]TD
关于方向导数的性质:
这意味着:[ ∇ f ( x k ) ] T D [\nabla f(x_k)]^T \mathcal D [∇f(xk)]TD达到最小值,意味着函数值下降的越剧烈。- 当 [ ∇ f ( x k ) ] T D > 0 ⇒ [\nabla f(x_k)]^T \mathcal D > 0 \Rightarrow [∇f(xk)]TD>0⇒在 x k x_k xk位置沿着 D \mathcal D D方向的函数值上升;反之, [ ∇ f ( x k ) ] T D < 0 ⇒ [\nabla f(x_k)]^T \mathcal D < 0 \Rightarrow [∇f(xk)]TD<0⇒在 x k x_k xk位置沿着 D \mathcal D D方向的函数值下降。
- ∣ ∇ f ( x k ) T D ∣ |\nabla f(x_k)^T \mathcal D| ∣∇f(xk)TD∣越大 ⇒ \Rightarrow ⇒ 上升/下降的越猛烈;反之, ∣ ∇ f ( x k ) T D ∣ |\nabla f(x_k)^T \mathcal D| ∣∇f(xk)TD∣越小 ⇒ \Rightarrow ⇒ 上升/下降的越平缓。
梯度下降法的特点
优点:
梯度下降法能够收敛,并且其下降方向被指定为负梯度方向 − ∇ f ( x k ) -\nabla f(x_k) −∇f(xk)。
缺陷:
-
收敛速度慢,即便是在凸函数甚至是强凸函数最快也只能达到线性收敛;
相关证明见:梯度下降法在强凸函数上的收敛性证明以及梯度下降法在凸函数上的收敛性。归纳:
-
梯度下降法仅使用负梯度方向作为搜索方向,换句话说:在考虑搜索方向的过程中,仅考虑了一阶梯度 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)信息;实际上,二阶梯度信息 ( Hessian Matrix ) (\text{Hessian Matrix}) (Hessian Matrix)也可以用来判断搜索方向。
-
其次,假设在最速下降法的过程中,由于方向 D k \mathcal D_k Dk已被确定,那么最优步长 α k \alpha_k αk是关于 ϕ ( α ) = f ( x k + α ⋅ D k ) \phi(\alpha) = f(x_k + \alpha \cdot \mathcal D_k) ϕ(α)=f(xk+α⋅Dk)的精确最小点:
α k = arg min α ϕ ( α ) = arg min α f ( x k + α ⋅ D k ) \alpha_k = \mathop{\arg\min}\limits_{\alpha} \phi(\alpha) =\mathop{\arg\min}\limits_{\alpha} f(x_k + \alpha \cdot \mathcal D_k) αk=αargminϕ(α)=αargminf(xk+α⋅Dk)
令 ϕ ′ ( α ) ≜ 0 \phi'(\alpha) \triangleq 0 ϕ′(α)≜0,必然有:
ϕ ′ ( α k ) = [ ∇ f ( x k + α k ⋅ D k ) ] T D k = [ ∇ f ( x k + 1 ) ] T [ − ∇ f ( x k ) ] = 0 \phi'(\alpha_k) = [\nabla f(x_k + \alpha_k \cdot \mathcal D_k)]^T \mathcal D_k = [\nabla f(x_{k+1})]^T[-\nabla f(x_k)] = 0 ϕ′(αk)=[∇f(xk+αk⋅Dk)]TDk=[∇f(xk+1)]T[−∇f(xk)]=0
这意味着:梯度向量 ∇ f ( x k + 1 ) \nabla f(x_{k+1}) ∇f(xk+1)与梯度向量 ∇ f ( x k ) \nabla f(x_k) ∇f(xk)垂直。
而这个垂直于Z \mathcal Z Z字形的缺陷是同一个缺陷:它仅能在迭代步骤中找到局部最优方向,而不是全局最优方向。也就是说:梯度下降法是一个贪心算法。
-
-
ZigZag \text{ZigZag} ZigZag现象:在迭代过程中,其收敛路径呈 Z \mathcal Z Z字形;
见下方代码示例与图像。可以看出:其搜索路径呈线 Z \mathcal Z Z字形,并且每一次迭代的方向均不是全局最优。 -
不具备二次终止性,也就是说:关于凸二次函数的最优化问题,仅仅通过有限次迭代步骤,无法收敛至最优解。
针对最速下降法缺陷代码示例
针对梯度下降法上述缺陷问题,以凸二次函数的最优化问题: min f ( x , y ) = 1 2 x 2 + 2 y 2 \begin{aligned}\min f(x,y) = \frac{1}{2} x^2 + 2 y^2\end{aligned} minf(x,y)=21x2+2y2为例,使用最速下降法近似求解最优解。对应代码表示如下:
import numpy as np
import math
import matplotlib.pyplot as pltdef f(x,y):return 0.5 * (x ** 2) + 2 * (y ** 2)def ConTourFunction(x,Contour):return math.sqrt(0.5 * (Contour - (0.5 * (x ** 2))))def Derfx(x):return xdef Derfy(y):return 4 * ydef GradientDescent(stepTime=10,epsilon=0.1):Start = (2.0,1.0)LocList = list()LocList.append(Start)for _ in range(stepTime):DerStart = (Derfx(Start[0]),Derfy(Start[1]))for step in list(np.linspace(0.0,1.0,1000)):Next = (Start[0] - (DerStart[0] * step),Start[1] - (DerStart[1] * step))DerfNext = Derfx(Next[0]) * (-1 * DerStart[0]) + Derfy(Next[1]) * (-1 * DerStart[1])if abs(DerfNext) <= epsilon:LocList.append(Next)Start = Nextepsilon /= 5.0breakContourList = [0.1,0.2,0.5,1.0]LimitParameter = 0.0001plt.figure(figsize=(10,5))for Contour in ContourList:# 设置范围时,需要满足x的定义域描述。x = np.linspace(-1 * math.sqrt(2 * Contour) + LimitParameter,math.sqrt(2 * Contour) - LimitParameter,200)y1 = [ConTourFunction(i,Contour) for i in x]y2 = [-1 * j for j in y1]plt.plot(x,y1,'--',c="tab:blue")plt.plot(x,y2,'--',c="tab:blue")plotList = list()for (x,y) in LocList:plotList.append((x,y))plt.scatter(x,y,s=50,facecolor="none",edgecolors="tab:red",marker='o')if len(plotList) < 2:continueelse:plt.plot([plotList[0][0],plotList[1][0]],[plotList[0][1],plotList[1][1]],c="tab:red")plotList.pop(0)plt.plot([0,2],[0,1],'--',c="tab:green")plt.show()if __name__ == '__main__':GradientDescent()
对应图像结果表示如下:

观察:其中绿色虚线表示全局最优方向;而红色线均与对应位置点所在等值线的切线相垂直;并且相邻路径间也垂直( Z \mathcal Z Z字形)。相比于全局最有方向,该方法过程中走了不少弯路~
而这里的弯路是指单次迭代步骤的最优方向。
该函数是一个凸二次函数,由于函数简单,因而代码中通过采样的方式来找出每次迭代步骤的近似最优解。但如果使用 Wolfe \text{Wolfe} Wolfe准则方式寻找迭代优质解,可能不会找的那么精确。随着迭代步骤的增加,最速下降法后期在最优解附近振动,而不容易收敛至最优解。
Reference \text{Reference} Reference:
最优化理论与方法-第六讲-无约束优化问题(二)
相关文章:

机器学习笔记之最优化理论与方法(七)无约束优化问题——常用求解方法(上)
机器学习笔记之最优化理论与方法——基于无约束优化问题的常用求解方法[上] 引言总体介绍回顾:线搜索下降算法收敛速度的衡量方式线性收敛范围高阶收敛范围 二次终止性朴素算法:坐标轴交替下降法最速下降法(梯度下降法)梯度下降法的特点 针对最速下降法缺…...
ES-索引管理
前言 数据类型 搜索引擎是对数据的检索,所以我们先从生活中的数据说起。我们生活中的数据总体分为两种: 结构化数据非结构化数据 结构化数据: 也称作行数据,是由二维表结构来逻辑表达和实现的数据,严格地遵循数…...

linux中常用shell脚本整理
linux常见shell脚本整理 备份日志 #!/bin/bash # 每日创建新的备份日志-根据日期备份 tar -czf log-date %Y%m%d.tar.gz /var/log # 通过crontab 每日定时启动 00 03 * * 5 /root/logbak.sh 监控内存和磁盘容量,小于给定值时报警 #!/bin/bash # 实…...

介绍PHP
PHP是一种流行的服务器端编程语言,用于开发Web应用程序。它是一种开源的编程语言,具有易学易用的语法和强大的功能。PHP支持在服务器上运行的动态网页和Web应用程序的快速开发。 PHP可以与HTML标记语言结合使用,从而能够生成动态的Web页面&a…...
selenium+find_elements用法
1、假如我们遇到多个标签的class一样,比如像下面这样的 我们可以采用js语法去定位,比如: document.getElementsByClassName("ant-calendar-picker-input ant-input")[0]...
1DM+下载器_11.2.1魔改增强版下载
1DM「原:IDM」下载器是一款安卓端的下载工具,多语言解锁版直安装版本,号称是目前 Android 平台最快、最先进的下载管理器应用「支持通过Torrent下载」,而这个版本是改线程的最新idm版本,可用来下载视频、音乐、电影、T…...
vue3:3、项目目录和关键文件
关于vsvode的更改 <!-- 加上setup允许在script中直接编写组合式api --> <script setup> // 组件引入后直接用 import HelloWorld from ./components/HelloWorld.vue import TheWelcome from ./components/TheWelcome.vue</script><!-- 1、js放在最上面&am…...
ChatGPT实战与私有化大模型落地
文章目录 大模型现状baseline底座选择数据构造迁移方法评价思考 领域大模型训练技巧Tokenizer分布式深度学习数据并行管道并行向量并行分布式框架——Megatron-LM分布式深度学习框架——Colossal-AI分布式深度学习框架——DeepSpeedP-tuning 微调 资源消耗模型推理加速模型推理…...
10分钟从实现和使用场景聊聊并发包下的阻塞队列
上篇文章12分钟从Executor自顶向下彻底搞懂线程池中我们聊到线程池,而线程池中包含阻塞队列 这篇文章我们主要聊聊并发包下的阻塞队列 阻塞队列 什么是队列? 队列的实现可以是数组、也可以是链表,可以实现先进先出的顺序队列,…...

Python入门学习13(面向对象)
一、类的定义和使用 类的使用语法: 创建类对象的语法: class Student:name None #学生的名字age None #学生的年龄def say_hi(self):print(f"Hi大家好,我是{self.name}")stu Student() stu.name &q…...

哈工大计算机网络课程网络安全基本原理之:身份认证
哈工大计算机网络课程网络安全基本原理之:身份认证 在日常生活中,在很多场景下我们都需要对当前身份做认证,比如使用密码、人脸识别、指纹识别等,这些都是身份认证的常用方式。本节介绍的身份认证,是在计算机网络安全…...

海外代购系统/代购网站怎么搭建
搭建海外代购系统/代购网站的详细步骤涉及到的内容非常多,本文将分为以下几个部分进行详细介绍:前端开发、后端管理系统的开发、数据库设计和代购流程的设计与实现。 一、前端开发 前端开发是整个代购网站的门面,它直接面向用户,…...

go-micro
go-micro Go Micro简介go-micro体系结构gin-go-micro使用consul实现服务注册与发现实现服务发现批量启动多个服务测试服务发现服务调用在微服务中使用ProtocolBuffergo-micro配置文件...
安装GPU驱动,CUDA Toolkit和配置与CUDA对应的Pytorch
如果有帮助,记得回来点个赞 目录 1.安装指定GPU驱动如果安装的GPU CUDA Version和CUDA Toolkit版本已经冲突怎么办? 2.安装指定版本的CUDA Toolkit如果我安装了CUDA Toolkit之后nvcc -V仍然显示旧的CUDA Toolkit版本怎么办? 3.安装与CUDA对应的Pytorch 1.安装指定GPU驱动 &…...

JavaScript单例模式
JavaScript单例模式 1 什么是单例模式2 实现一个基础的单例模式3 透明的单例模式4 用代理实现单例模式5 JavaScript 中的单例模式6 惰性单例 1 什么是单例模式 保证一个类只有一个实例,并提供一个访问它的全局访问点,这就是单例模式。 单例模式是一种常…...

centos下安装jenkins.war
https://get.jenkins.io/war-stable/ 下载jenkins.war包,(2.164.1 版本支持1.8,其他的都是jdk11),可以安装完成后更新jenkins.war的安装包启动jenkins命令 java -jar jenkins.war --httpPort8010访问http://IP:8010/jenkins (密码在/root/.jenkins/secre…...

App线上网络问题优化策略
在我们App开发过程中,网络是必不可少的,几乎很难想到有哪些app是不需要网络传输的,所以网络问题一般都是线下难以复现,一旦到了用户手里就会碰到很多疑难杂症,所以对于网络的监控是必不可少的,针对用户常见…...
PDF 工具箱
PDF 工具箱 V9.0.0.1 程序:VB.net 运行库:NET Framework 4.5 功能简介: 1、PDF文件多文件合并,可调整顺序。 2、PDF文件拆分,将每页拆分成独立的PDF文件。 3、PDF文件添加水印,文字或图片水印&…...

大数据组件系列-Hadoop每日小问
1、谈谈对HDFS的理解?HDFS这种存储适合哪些场景? HDFS即Hadoop Distributed File System,Hadoop 分布式文件系统。它为的是解决海量数据的存储与分析的问题,它本身是源于Google在大数据方面的论文,GFS-->HDFS; HD…...
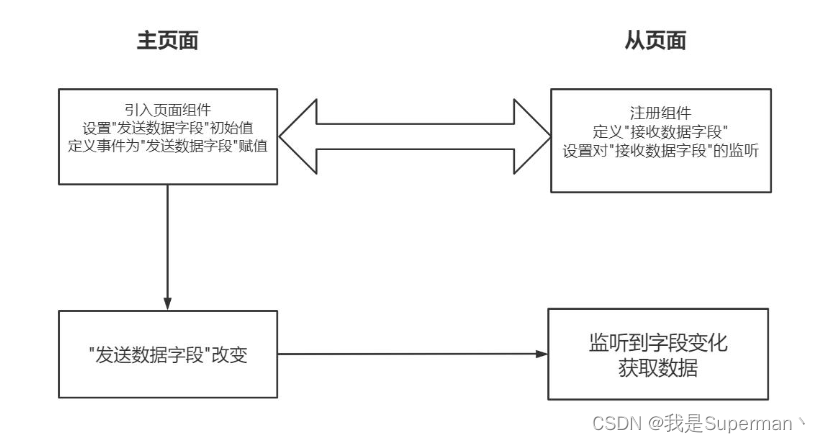
【前端】在Vue页面中引入其它vue页面 数据传输 相互调用方法等
主页面 home 从页面 headView 需求 在 home.vue 中引用 headView.Vue 方案: home.vue 代码: 只需要在home.vue 想要的地方添加 <headView></headView> <script>//聊天页面 import headView /view/headView.vueexport default {components: {headView},…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
