nginx 常用配置之 pass_proxy
大家好,我是 17。
今天和大家聊聊 pass_proxy 代理。
pass_proxy 代理
在前端代理主要是为了跨域。虽然前端跨域有多种方法,各有利弊,但用代理来跨域对开发是最友好的。用代理可以不用修改产品代码切换线上线下,非常安全。pass_proxy 默认会把 cookie 也一同转发。 常用的配置非常简单。
不带斜杠
前端 /api/user
后端 /api/user
location ^~ /api/ {proxy_pass http://127.0.0.1:3001;}
不带斜杠把 path 直接拼接在 url后面;
带斜杠
前端 /api/user
后端 /user
location ^~ /api/ {proxy_pass http://127.0.0.1:3001/;}
带斜杠会先去掉匹配到的 path, 再拼接。
正则匹配的时候不能带斜杠
~ 区分大小写正则匹配 ,~* 不区分大小写正则匹配 。location 用正则匹配的时候,proxy_pass 后面不能以 / 结尾,因为 nginx 不能处理这种情况。
location ~ /api/ {proxy_pass http://127.0.0.1:3001/;}
本例中,请求 localhost:3000/ 会导致 nginx 报错。
斜杠后面加路径
前端 /api/user
后端 /web/api/user
location ^~ /api/ {proxy_pass http://127.0.0.1:3001/web$request_uri;}
代理之前rewrite
location /search/ {rewrite /search/([^/]+) /s?wd=$1 break;proxy_pass http://127.0.0.1:3001;
}
服务端获取真实ip
反向代理: 简单来说 proxy_pass 把请求转发到其它服务地址的时候,就是反向代理。
如果是客户端与服务器直接连接,nginx 变量 $remote_addr 就可以拿到真实ip。$remote_addr 是不能伪造的。但是如果客户端是经过反向代理连接的服务器,服务器能拿到的只有代理服务器的 IP。为了能拿到客户端真实 IP,代理服务器在转发的时候需要加上一个 http 扩展头部 X-Forwarded-For。
所有代理的 ip 依次列出来,从远及近。
X-Forwarded-For: IP0, IP1, IP2
X-Forwarded-For 是一个 HTTP 扩展头部。HTTP/1.1(RFC 2616)协议并没有对它的定义,它最开始是由 Squid 这个缓存代理软件引入,用来表示 HTTP 请求端真实 IP。如今它已经成为事实上的标准,被各大 HTTP 代 理、负载均衡等转发服务广泛使用,并被写入 RFC 7239(Forwarded HTTP Extension)标准之中。
location /api/ {
proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
proxy_pass http://127.0.0.1:3000/;}
$proxy_add_x_forwarded_for变量包含客户端请求头中的"X-Forwarded-For",与$remote_addr用逗号分开,如果没有"X-Forwarded-For" 请求头,则$proxy_add_x_forwarded_for等于$remote_addr。$remote_addr变量的值是客户端的IP。
可能你会担心,ip会不会被伪造。即使客户端伪造了 ip,nginx 也会用真实的 ip 进行重置。所以 $remote_addr 是可信的。
相关文章:

nginx 常用配置之 pass_proxy
大家好,我是 17。 今天和大家聊聊 pass_proxy 代理。 pass_proxy 代理 在前端代理主要是为了跨域。虽然前端跨域有多种方法,各有利弊,但用代理来跨域对开发是最友好的。用代理可以不用修改产品代码切换线上线下,非常安全。pass…...

Linux中驱动模块加载方法分析
如何管理驱动模块 由于Linux驱动模块众多,系统对模块加载顺序有要求,一些基础模块在系统启动时需要很早就被加载;开发者加入自己的模块时,需要维护一个模块初始化列表,上面两方面的做起来很困难,为了科学地…...

yarn 通过 resolutions,指定子孙依赖包版本号,解决froala-editor 版本问题
前端开发项目过程中会使用到各种依赖包。但是这些依赖包虽然好用,但是一味使用最新版本可能会出现各种奇葩问题,因此我们经常会针对一些依赖包指定一个稳定版本。 常用版本 版本号注释“1.0.2”必须切到1.0.2版“>1.0.2”必须大于1.0.2版“>1.0.…...
Elasticsearch7.8.0版本进阶——多文档操作流程
目录一、多文档操作1.1、多文档操作的概述1.2、多文档操作与单文档模式区别二、用单个 mget 请求取回多个文档2.1、用单个 mget 请求取回多个文档的图解2.2、用单个 mget 请求取回多个文档的步骤三、bulk API 的模式请求取回多个文档3.1、bulk API 的模式请求取回多个文档的图解…...
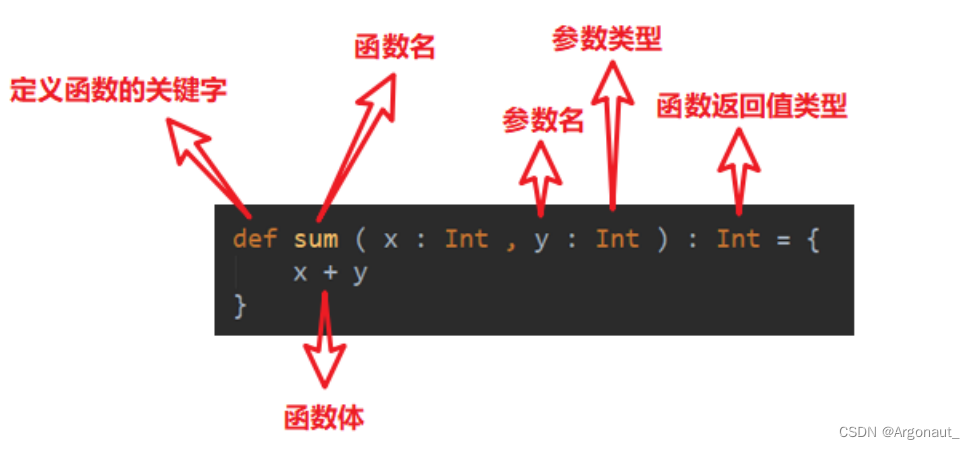
Scala函数式编程(第五章:函数基础、函数高级详解)
文章目录第 5 章 函数式编程5.1 函数基础5.1.1 函数基本语法5.1.2 函数和方法的区别5.1.3 函数定义5.1.4 函数参数5.1.5 函数至简原则(重点)5.2 函数高级5.2.1 高阶函数5.2.2 匿名函数5.2.3 高阶函数案例5.2.4 函数柯里化&闭包5.2.5 递归5.2.6 控制抽…...

ZED相机快速使用指南
1、安装SDK ZED SDK 3.8 - Download | Stereolabs 2、安装ros GitHub - stereolabs/zed-ros-wrapper: ROS wrapper for the ZED SDK 其他教程:ZED2相机SDK安装使用及ROS下使用_可即的博客-CSDN博客 3、官方文档 Get Started with ZED | Stereolabs 4、标定参…...
树莓派4b配置OpenWrt联网
文章目录前言一、下载固件二、配置wan口三、简单介绍1、修改无线名称、设置密码2、下载软件包总结前言 树莓派4b内置wifi模块,加一个千兆网口 好像有一种办法,通过无线wifi链接其他wifi通网,然后把这个网口作为lan口,连接电脑使…...

不同语言下的定时器,你都掌握了吗?
我们大家都对定时器不陌生,无论是现实中还是项目中,都离不开定时。在现实中,它叫闹钟,在项目上,它叫定时器,即定时触发某件事情。它能帮助我们在某一个既定的时间节点上,来提醒我们做一些事情&a…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 水仙花数(Python) | 机试题+算法思路+考点+代码解析 【2023】
水仙花数 题目 所谓的水仙花数是指一个n位的正整数其各位数字的n次方的和等于该数本身, 例如153 = 1^3 + 5^3 + 3^3,153是一个三位数 输入 第一行输入一个整数N, 表示 N 位的正整数 N 在3-7之间包含3,7 第二行输入一个正整数M, 表示需要返回第M个水仙花数 输出描述 返…...

在onBindViewHolder设置View的translation失败或错乱的问题
这个问题,可以换成“为什么在onCreate里面修改一些子View不生效,错位,乱”等问题。 本质原因肯定是在没有把整个ViewGroup渲染完成之前,操作了部分子View,导致了位置偏移等。 解决办法也很简单,通过调用Vi…...

【2.21】MySQL索引、动态规划、学习方法
索引常见面试题 什么是索引 索引的定义就是帮助存储引擎快速获取数据的一种数据结构,形象的说就是索引是数据的目录。存储引擎,说白了就是如何存储数据、如何为存储的数据建立索引和如何更新、查询数据等技术的实现方法。索引和数据就是位于存储引擎。…...
| 包含代码编写思路)
华为OD机试题 - 二叉树层次遍历(JavaScript)| 包含代码编写思路
最近更新的博客 华为OD机试题 - 字符串加密(JavaScript) 华为OD机试题 - 字母消消乐(JavaScript) 华为OD机试题 - 字母计数(JavaScript) 华为OD机试题 - 整数分解(JavaScript) 华为OD机试题 - 单词反转(JavaScript) 华为OD机试题 最近更新的博客使用说明二叉树层次遍…...

力扣解法汇总1140. 石子游戏 II
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣 描述: 爱丽丝和鲍勃继续他们的石子游戏。许多堆石子 排成一行,每堆都有正整…...

Kerberos认证原理与使用教程
Kerberos认证原理与使用教程 一、Kerberos 概述 二、什么是 Kerberos Kerberos 是一种计算机网络认证协议,用来在非安全网络中,对个人通信以安全的手段进行身份认证。这个词又指麻省理工学院为这个协议开发的一套计算机软件。软件设计上采用客户端…...
内存取证常见例题思路方法-volatility (没有最全 只有更全)
目录 1.从内存文件中获取到用户hacker 的密码并且破解密码,将破解后的密码作为 Flag值提交; 2.获取当前系统的主机名,将主机名作为Flag值提交; 3.获取当前系统浏览器搜索过的关键词,作为Flag提交; 4.获取当前内存文件的 ip地址 5.当前系…...
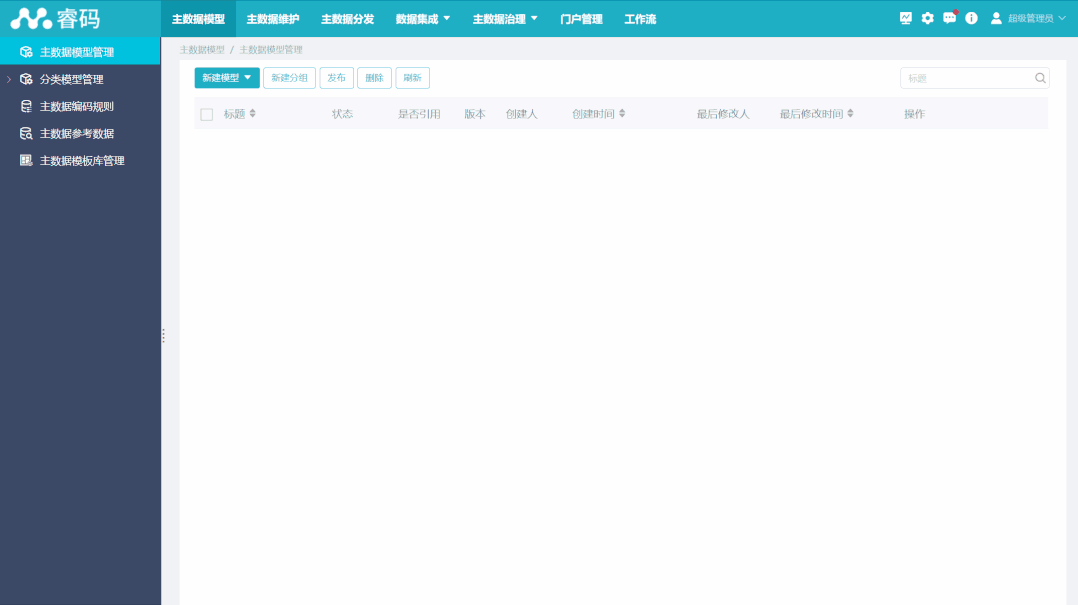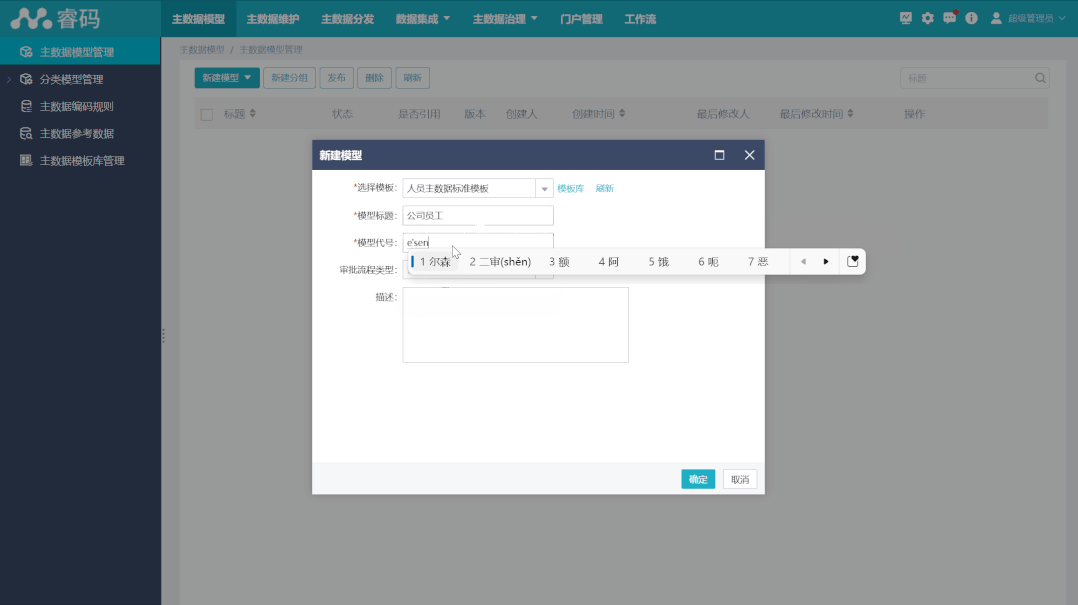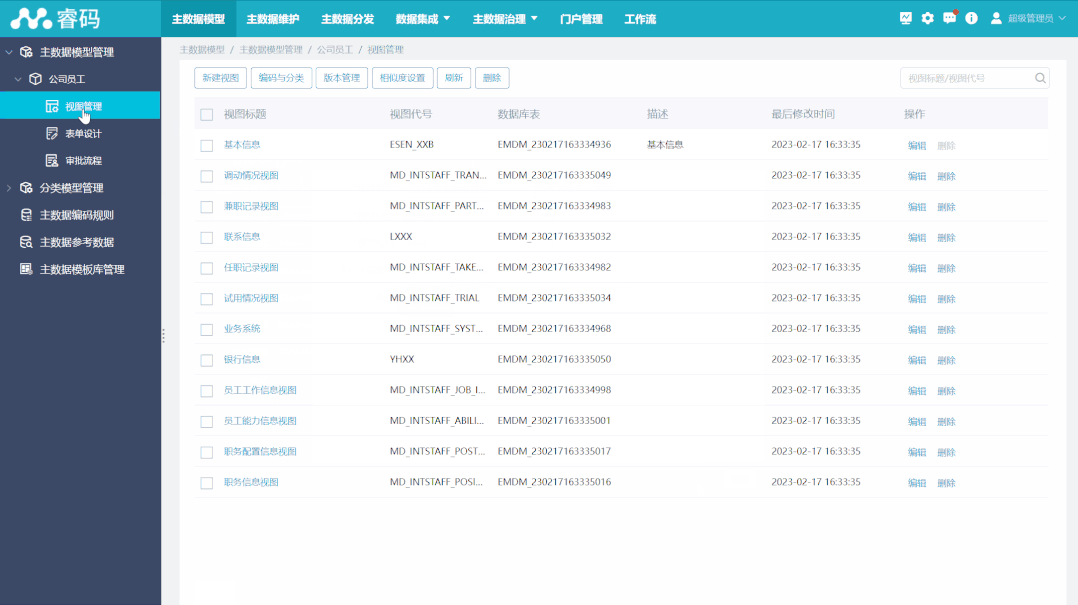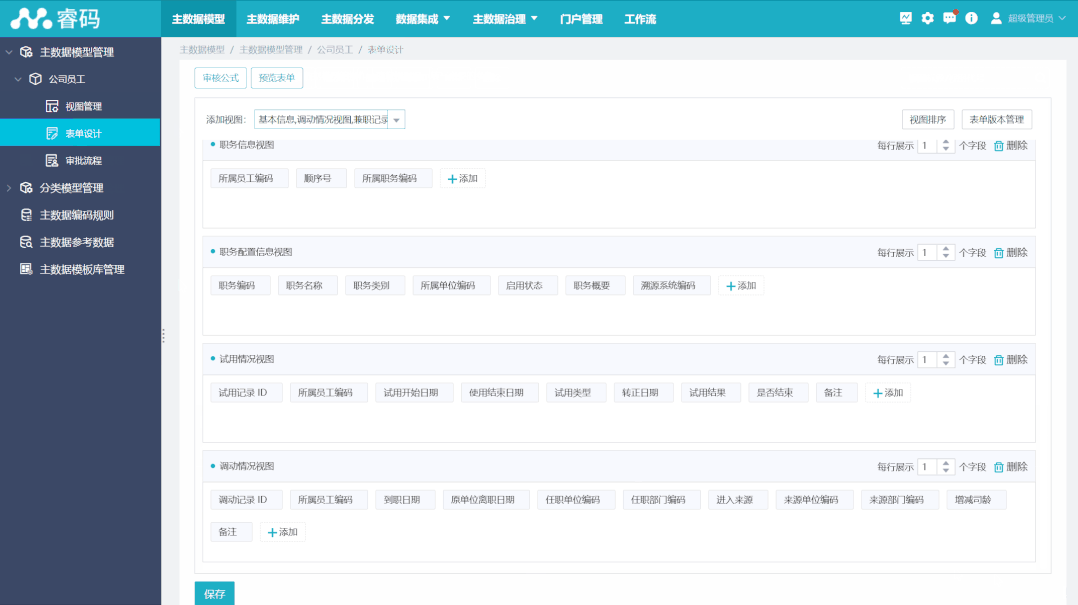
10 种主数据模型设计示例分享,推荐收藏
主数据模型是主数据管理的基础,一个完整的、可扩展的、相对稳定的主数据模型对于主数据管理的成功起着重要的作用。规划、创建主数据模型的过程,是梳理主数据管理体系的过程,目的是建立一个良好的资源目录结构,划分合理的资源粒度…...

React学习笔记
React学习笔记 概述 React是用于构建用户界面的JavaScript库。 现在前端领域最为流行的三大框架: VueReactAngular 其中,Vue和React是国内最为流行的两个框架。 React的特点: 1、声明式编程:它允许我们只需要维护自己的状态…...
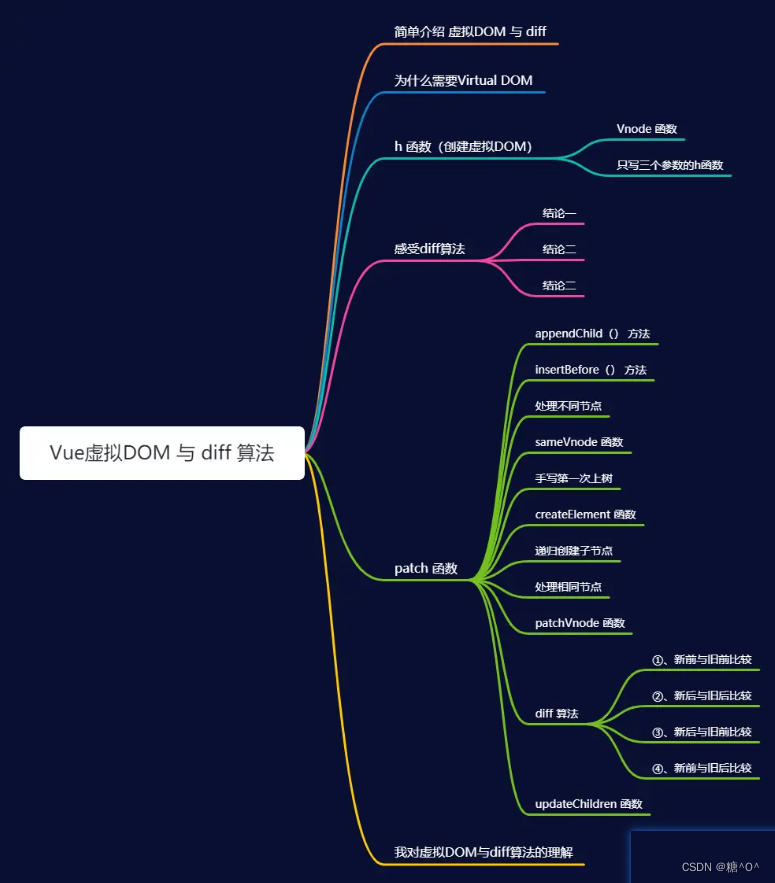
【Vue源码解析】Vue虚拟dom和diff算法
Vue虚拟dom和diff算法1. 简介2. 搭建环境1. 安装snabbdom2. 安装webpack5并配置3、函数3.1 虚拟节点vnode的属性3.2 使用h函数 创建虚拟节点3.3 使用patch函数 将虚拟节点上DOM树3.4 h函数嵌套使用,得到虚拟DOM树(重要)3.5 patchVnode函数3.6…...

算法学习与填充计划---2023.2.21---夏目
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石.CSDN 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:ACM周训练题目合集.CSDN 💬总结:…...
JavaScript中怎么实现链表?
JavaScript中怎么实现链表? 学习数据结构的的链表和树时,会遇到节点(node)这个词,节点是处理数据结构的链表和树的基础。节点是一种数据元素,包括两个部分:一个是实际需要用到的数据;…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
