【2.21】MySQL索引、动态规划、学习方法
索引常见面试题
什么是索引
- 索引的定义就是帮助存储引擎快速获取数据的一种数据结构,形象的说就是索引是数据的目录。
- 存储引擎,说白了就是如何存储数据、如何为存储的数据建立索引和如何更新、查询数据等技术的实现方法。索引和数据就是位于存储引擎。
索引的分类
- 按「数据结构」分类:B+tree索引、Hash索引、Full-text索引。
- 创建的主键索引和二级索引默认使用的是 B+Tree 索引。
- B+Tree 存储千万级数据只需要 3-4 层高度就可以满足,从千万级的表查询目标数据最多需要 3-4 次磁盘 I/O。
- 先检索二级索引,找到对应的叶子节点获取主键值,然后通过聚簇索引中的B+Tree 树查询到对应的叶子节点,要查两个 B+Tree 才能查到数据,这个过程叫做回表。
- 在二级索引的 B+Tree 就能查询到结果的过程就叫作「覆盖索引」,也就是只需要查一个 B+Tree 就能找到数据。
- 按「物理存储」分类:聚簇索引(主键索引)、二级索引(辅助索引)。
- 主键索引的 B+Tree 的叶子节点存放的是实际数据,所有完整的用户记录都存放在主键索引的 B+Tree 的叶子节点里。术语“聚簇”表示数据行和相邻的键值聚簇地存储在一起。
- 二级索引的 B+Tree 的叶子节点存放的是主键值,而不是实际数据。
- 按「字段特性」分类:主键索引、唯一索引、普通索引、前缀索引。
- 主键索引就是建立在主键字段上的索引,通常在创建表的时候一起创建,一张表最多只有一个主键索引,索引列的值不允许有空值。
- 唯一索引建立在 UNIQUE 字段上的索引,一张表可以有多个唯一索引,索引列的值必须唯一,但是允许有空值。
- 普通索引就是建立在普通字段上的索引,既不要求字段为主键,也不要求字段为 UNIQUE。
- 前缀索引是指对字符类型字段的前几个字符建立的索引,而不是在整个字段上建立的索引,前缀索引可以建立在字段类型为 char、 varchar、binary、varbinary 的列上。使用前缀索引的目的是为了减少索引占用的存储空间,提升查询效率
- 按「字段个数」分类:单列索引、联合索引。
- 通过将多个字段组合成一个索引,该索引就被称为联合索引。
- 联合索引的最左匹配原则,在遇到范围查询(如 >、<)的时候,就会停止匹配
- 建立联合索引时,要把区分度大的字段排在前面,这样区分度大的字段越有可能被更多的 SQL 使用到。
什么时候需要 / 不需要创建索引?
-
索引也是有缺点的,比如:
-
需要占用物理空间,数量越大,占用空间越大;
-
创建索引和维护索引要耗费时间,这种时间随着数据量的增加而增大;
-
会降低表的增删改的效率,因为每次增删改索引,B+ 树为了维护索引有序性,都需要进行动态维护
-
-
什么时候适用索引?
- 字段有唯一性限制的,比如商品编码。
- 经常用于
WHERE查询条件的字段,这样能够提高整个表的查询速度,如果查询条件不是一个字段,可以建立联合索引。 - 经常用于
GROUP BY和ORDER BY的字段,这样在查询的时候就不需要再去做一次排序了,因为我们都已经知道了建立索引之后在 B+Tree 中的记录都是排序好的。
-
什么时候不需要创建索引?
WHERE条件,GROUP BY,ORDER BY里用不到的字段,索引的价值是快速定位,如果起不到定位作用的字段通常是不需要创建索引的,因为索引是会占用物理空间的。- 字段中存在大量重复数据,不需要创建索引,MySQL 有一个查询优化器,查询优化器发现某个值出现在表的数据行中的百分比很高的时候,它一般会忽略索引,进行全表扫描。
- 表数据太少的时候,不需要创建索引。
- 经常更新的字段不用创建索引,比如不要对电商项目的用户余额建立索引,因为索引字段频繁修改,由于要维护 B+Tree的有序性,那么就需要频繁的重建索引,这个过程是会影响数据库性能的。
有什么优化索引的方法?
- 前缀索引优化:使用某个字段中字符串的前几个字符建立索引。可以减小索引字段大小,节省空间。可以增加一个索引页存储前缀索引值,提高索引查询速度。
- 前缀索引有一定的局限性,例如:
- order by 就无法使用前缀索引;
- 无法把前缀索引用作覆盖索引;
- 前缀索引有一定的局限性,例如:
- 覆盖索引优化:SQL 中查询的所有字段,在索引 B+Tree 的叶子节点上都能找得到的那些索引,从二级索引中查询得到记录,而不需要通过聚簇索引查询整行记录的所有信息,可以避免回表的操作。
- 主键索引最好是自增的:如果我们使用自增主键,那么每次插入的新数据就会按顺序添加到当前索引节点的位置,不需要移动已有的数据,当页面写满,就会自动开辟一个新页面。因为每次插入一条新记录,都是追加操作,不需要重新移动数据,因此这种插入数据的方法效率非常高。
- 如果我们使用非自增主键,可能产生页分裂。页分裂还有可能会造成大量的内存碎片,导致索引结构不紧凑,从而影响查询效率。
- 索引列最好设置为NOT NULL约束
- 第一原因:索引列存在 NULL 就会导致优化器在做索引选择的时候更加复杂,更加难以优化,因为可为 NULL 的列会使索引、索引统计和值比较都更复杂,比如进行索引统计时,count 会省略值为NULL 的行。
- 第二个原因:NULL 值是一个没意义的值,但是它会占用物理空间。
防止索引失效
发生索引失效的情况:
- 当我们使用左或者左右模糊匹配的时候,也就是
like %xx或者like %xx%这两种方式都会造成索引失效。- like %xx:查询后缀为xx的数据。
- 因为索引 B+ 树是按照「索引值」有序排列存储的,只能根据前缀进行比较。
- 索引列发生改变:当我们在查询条件中对索引列进行计算、使用函数,这些情况下都会造成索引失效。
- 因为索引保存的是索引字段的原始值,而不是经过计算后的值。
- MySQL 在遇到字符串和数字比较的时候,会自动把字符串转为数字,然后再进行比较。如果字符串是索引列,而输入的参数是数字的话,那么索引列会发生隐式类型转换,由于隐式类型转换是通过 CAST 函数实现的,等同于对索引列使用了函数,所以就会导致索引失效。
- 联合索引要能正确使用需要遵循最左匹配原则,也就是按照最左优先的方式进行索引的匹配,否则就会导致索引失效。
- 索引下推优化(index condition pushdown), 可以在联合索引遍历过程中,对联合索引中包含的字段先做判断,直接过滤掉不满足条件的记录,减少回表次数。
- 在 WHERE 子句中,如果在 OR 前的条件列是索引列,而在 OR 后的条件列不是索引列,那么索引会失效。
- 因为 OR 的含义就是两个只要满足一个即可,因此只有一个条件列是索引列是没有意义的,只要有条件列不是索引列,就会进行全表扫描。
LeetCode
-
leetcode494
既然为target,那么就一定有 left组合 - right组合 = target。
left + right = sum,而sum是固定的。right = sum - left
公式来了, left - (sum - left) = target 推导出 left = (target + sum)/2 。
target是固定的,sum是固定的,left就可以求出来。
假设加法总和为x,减法总和为sum - x。x = (target + sum) / 2。
问题转化为:装满容量x的背包,有几种方法?是一个组合问题。
-
dp数据及其下标含义:dp[j]表示装满 j 容积的背包,有dp[j]种装法。
-
确定递推公式:
所以,递推公式为:
dp[j] += dp[j - nums[i]]。后面还会用到这种递推公式。 -
dp数组如何初始化:dp[0] = 1,因为当x为0时,有1种组合方案。
-
确定遍历顺序:与之前类似,外层遍历nums,内层倒序遍历x。
-
举例推导dp数组
class Solution {public int findTargetSumWays(int[] nums, int target) {/**//01背包问题:left - right = target。right = sum - leftleft = (target + sum) / 2*/int sum = 0;for(int i : nums){sum += i;}if(sum < Math.abs(target)){return 0;}if((target + sum) % 2 != 0){return 0;}int size = (target + sum) / 2;int dp [] = new int [size + 1];dp[0] = 1;for(int i = 0 ;i < nums.length ;i ++){for(int j = size;j >= nums[i]; j --){dp[j] += dp[j - nums[i]];}}return dp[size];} } -
-
leetcode474
给定背包容量(可以装m个0和n个1)求背包可以装满的最大容量(最大子集)。strs[ i ] 看作是1个物品,只不过是将0和1两个不同的维度分开。该物品的价值为一个子集。最大容量(最大子集)为
dp[m][n]。-
dp数组及下标含义:
dp[i][j]表示i个0和j个1的strs的最大子集。 -
确定递推公式:
dp[i][j] = Math.max(dp[i][j] , dp[i - zeorNum][j - oneNum] + 1) -
dp数组初始化:初始化为0即可。
-
遍历顺序:物品就是strs里的字符串,背包容量就是题目描述中的m和n。所以外层正序遍历zreoNum,内层倒序遍历oneNum。
-
举例推导:
-
class Solution {public int findMaxForm(String[] strs, int m, int n) {int dp [] [] = new int [m + 1][n + 1];for(String s : strs){int zeroNum = 0 , oneNum = 0;for(int i = 0 ;i < s.length() ;i ++){char c = s.charAt(i);if(c == '0'){zeroNum ++;}else oneNum ++;}//外层for循环表示每次取物体放入背包。//该for循环表示两个维度的具体计算。for(int i = m ;i >= zeroNum ;i --){for(int j = n ;j >= oneNum ; j --){dp[i][j] = Math.max(dp[i][j] , dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
}
完全背包理论基础
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
01背包的一维dp数组内层背包容量是从大到小遍历,因为每件物品只有一件,要保证只放入一次。而完全背包不同,每件物品有无数件,所以从小到大遍历即可。
for(int i = 0;i < n ;i ++){ //先遍历物品for(int j = weight[i];j <= bagWeight; j ++){ //再遍历背包dp[j] = Math.max(dp[j] , dp[j - weight[i]] + values[i]);}
}
for(int j = 0;j <= bagWeight;j ++){ //先遍历背包for(int i = 0;i < n;i ++){ //后遍历物品if(j - weight[i] >=0) dp[j] = Math.max(dp[j] , dp[j - weight[i]] + values[i]);}
}
LeetCode
-
leetcode 518
注意,该题是求组合数,所以用递推公式:
dp[j] += dp[j - coins[i]]。在求装满背包有几种方案的时候,难点在于遍历顺序:
如果求组合数就是外层for循环遍历物品,内层for遍历背包。(正常遍历顺序,组合数不分数字先后)
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
class Solution {public int change(int amount, int[] coins) {int n = coins.length;int dp [] = new int [amount + 1];dp[0] = 1;for(int i = 0 ;i < n;i ++){for(int j = coins[i]; j <= amount; j ++){dp[j] += dp[j - coins[i]];}}return dp[amount];} }
相关文章:

【2.21】MySQL索引、动态规划、学习方法
索引常见面试题 什么是索引 索引的定义就是帮助存储引擎快速获取数据的一种数据结构,形象的说就是索引是数据的目录。存储引擎,说白了就是如何存储数据、如何为存储的数据建立索引和如何更新、查询数据等技术的实现方法。索引和数据就是位于存储引擎。…...
| 包含代码编写思路)
华为OD机试题 - 二叉树层次遍历(JavaScript)| 包含代码编写思路
最近更新的博客 华为OD机试题 - 字符串加密(JavaScript) 华为OD机试题 - 字母消消乐(JavaScript) 华为OD机试题 - 字母计数(JavaScript) 华为OD机试题 - 整数分解(JavaScript) 华为OD机试题 - 单词反转(JavaScript) 华为OD机试题 最近更新的博客使用说明二叉树层次遍…...

力扣解法汇总1140. 石子游戏 II
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣 描述: 爱丽丝和鲍勃继续他们的石子游戏。许多堆石子 排成一行,每堆都有正整…...

Kerberos认证原理与使用教程
Kerberos认证原理与使用教程 一、Kerberos 概述 二、什么是 Kerberos Kerberos 是一种计算机网络认证协议,用来在非安全网络中,对个人通信以安全的手段进行身份认证。这个词又指麻省理工学院为这个协议开发的一套计算机软件。软件设计上采用客户端…...
内存取证常见例题思路方法-volatility (没有最全 只有更全)
目录 1.从内存文件中获取到用户hacker 的密码并且破解密码,将破解后的密码作为 Flag值提交; 2.获取当前系统的主机名,将主机名作为Flag值提交; 3.获取当前系统浏览器搜索过的关键词,作为Flag提交; 4.获取当前内存文件的 ip地址 5.当前系…...
10 种主数据模型设计示例分享,推荐收藏
主数据模型是主数据管理的基础,一个完整的、可扩展的、相对稳定的主数据模型对于主数据管理的成功起着重要的作用。规划、创建主数据模型的过程,是梳理主数据管理体系的过程,目的是建立一个良好的资源目录结构,划分合理的资源粒度…...

React学习笔记
React学习笔记 概述 React是用于构建用户界面的JavaScript库。 现在前端领域最为流行的三大框架: VueReactAngular 其中,Vue和React是国内最为流行的两个框架。 React的特点: 1、声明式编程:它允许我们只需要维护自己的状态…...
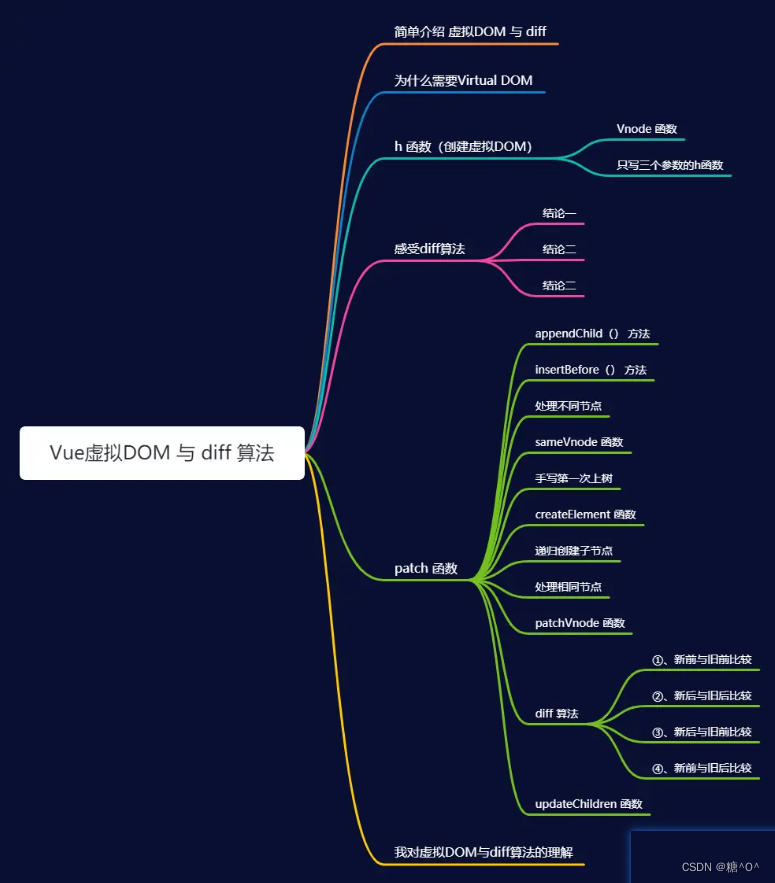
【Vue源码解析】Vue虚拟dom和diff算法
Vue虚拟dom和diff算法1. 简介2. 搭建环境1. 安装snabbdom2. 安装webpack5并配置3、函数3.1 虚拟节点vnode的属性3.2 使用h函数 创建虚拟节点3.3 使用patch函数 将虚拟节点上DOM树3.4 h函数嵌套使用,得到虚拟DOM树(重要)3.5 patchVnode函数3.6…...

算法学习与填充计划---2023.2.21---夏目
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石.CSDN 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:ACM周训练题目合集.CSDN 💬总结:…...
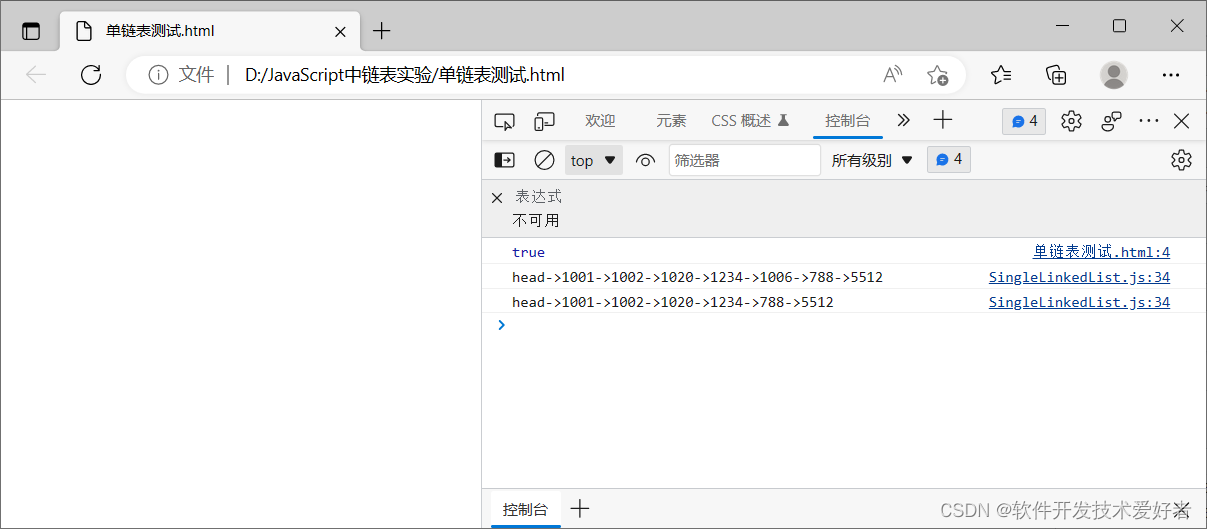
JavaScript中怎么实现链表?
JavaScript中怎么实现链表? 学习数据结构的的链表和树时,会遇到节点(node)这个词,节点是处理数据结构的链表和树的基础。节点是一种数据元素,包括两个部分:一个是实际需要用到的数据;…...

多孔弹性材料中传播的膨胀波方法(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

时间复杂度与空间复杂度
目录一、算法的复杂度二、时间复杂度2.1 什么叫时间复杂度2.2 大O的渐进表示法2.3 计算时间复杂度的练习三、空间复杂度四、常见复杂度的对比一、算法的复杂度 算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏…...
UDP报文详解
目录 🐳今日良言:走好选择的路,别选择好走的路,你才能拥有真正的自己。 🐼一、UDP协议特点 🐼二、UDP协议段格式详解 🐳今日良言:走好选择的路,别选择好走的路,你才能拥有真正的自…...

C#开发的OpenRA的NextPowerOf2
C#开发的OpenRA的NextPowerOf2 在游戏里,经常需要对计算资源进行优化。 比如屏幕的大小,以及缓冲区的大小,还有纹理的大小。 由于计算机都是基于二进制的原理,那么它的最快计算速度,就是让计算的数字都是2的n次方。 基于此策略,在程序里就需要计算出来最接近2的n次方的数…...
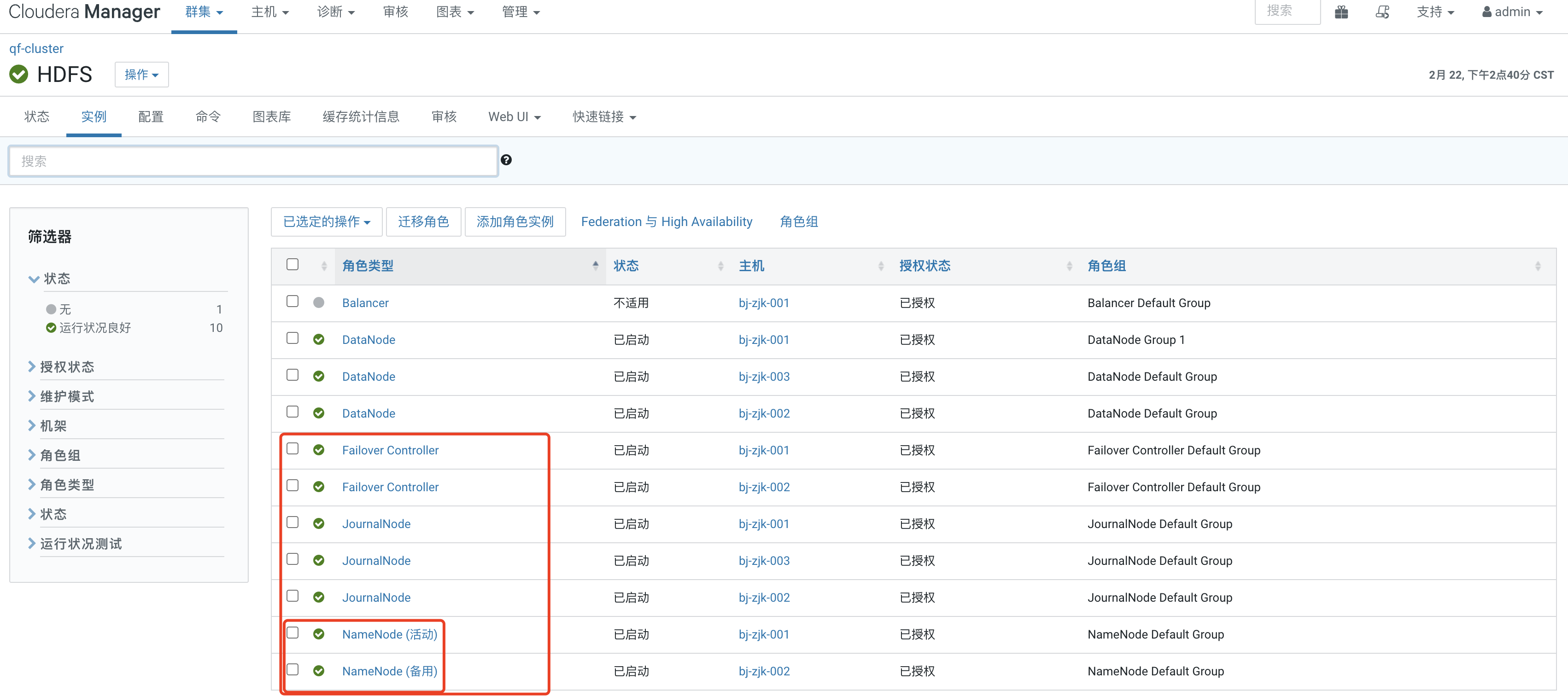
CDH 6.3.2启用HDFS高可用
启用原因 CDH 6.3.2平台即将用于生产,生产平台几乎需要高可用平台,故需要升级CDH中的HDFS为HA。 启用准备 CDH已经成功安装并正常使用CMS的管理员账号正常登陆 HDFS启用HA 登陆CMS系统->选择HDFS服务->点击进入到HDFS服务详情页面,…...
多服务器节点访问解决一人一单问题+redis设置锁方案
项目地址及项目具体介绍-码云仓库:https://gitee.com/flowers-bloom-is-the-sea/distributeNodeSolvePessimisticLockByRedis 测试1: 这里使用jmeter同时启动2各线程: 原来的数据库表的数据: goods的数据是: id …...

tensorflow 学习笔记(三):神经网络八股
本节内容: 前两节使用 Tensorflow2 的原生代码大叫神经网络。本节使用 keras 搭建神经网络(八股:六步法,有 Sequential 和 class 两种)。 文章目录一、搭建网络八股 sequential1.1、keras 介绍1.2、六步法搭建 keras …...
)
华为OD机试真题Python实现【射击比赛】真题+解题思路+代码(20222023)
射击比赛 题目 给定一个射击比赛成绩单 包含多个选手若干次射击的成绩分数 请对每个选手按其最高三个分数之和进行降序排名 输出降序排名后的选手 ID 序列 条件如下: 一个选手可以有多个射击成绩的分数 且次序不固定如果一个选手成绩小于三个 则认为选手的所有成绩无效 排名忽…...
(结论)(数学))
【YBT2023寒假Day12 C】树的计数 II(prufer)(结论)(数学)
树的计数 II 题目链接:YBT2023寒假Day12 C 题目大意 给你一个长度为 n 的排列 p,问你有多少个不同的有标号无根树,满足如果 i,j 有边那 pi,pj 也有边。 思路 首先可以把排列变成置换环。 注意到是树,发现一个置换中似乎不太可…...

深入浅出C++ ——多态
文章目录一、多态的概念二、多态的定义及实现1. 多态的构成条件2. 虚函数3. 虚函数的重写4. virtual的使用:5. 虚函数重写的两个例外:6. C11 override 和 final7. 重载、重写、重定义的对比三、抽象类四、多态的原理1. 虚函数表2. 多态的原理3. 静态绑定…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...
