时间复杂度与空间复杂度
目录
- 一、算法的复杂度
- 二、时间复杂度
- 2.1 什么叫时间复杂度
- 2.2 大O的渐进表示法
- 2.3 计算时间复杂度的练习
- 三、空间复杂度
- 四、常见复杂度的对比
一、算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
二、时间复杂度
2.1 什么叫时间复杂度
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数(即最高阶的数量级),那么这里我们使用大O的渐进表示法。
例如:
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
该函数一共执行了N^2+2*N+10次,取最高阶的数量级那就是N^2
所以该函数的时间复杂度是N^2
2.2 大O的渐进表示法
大O符号 (Big O notation) 是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
在一个长度为N数组中搜索一个数据x。
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.3 计算时间复杂度的练习
1、
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}时间复杂度为:O(N)
2、
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}时间复杂度为:O(M+N)
3、
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}时间复杂度为:O(1)
4、
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character );时间复杂度为:O(N)
5、
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}时间复杂度为:O(N^2)
6、
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}时间复杂度:O(log n)
7、
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}时间复杂度是:O(N)
8、
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}时间复杂度是:O(2^N)
三、空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
示例一:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}空间复杂度为:O(1)
示例二:
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) *sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}空间复杂度为:O(N)
示例三:
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}空间复杂度:O(N)
四、常见复杂度的对比
一般算法常见的复杂度如下:

你学会了吗?如果对你有帮助的话,请动动您的手指,点亮一下小心心哈,想学习更多的有关数据结构的内容,点点关注哦,后期会持续更新哈!
相关文章:

时间复杂度与空间复杂度
目录一、算法的复杂度二、时间复杂度2.1 什么叫时间复杂度2.2 大O的渐进表示法2.3 计算时间复杂度的练习三、空间复杂度四、常见复杂度的对比一、算法的复杂度 算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏…...
UDP报文详解
目录 🐳今日良言:走好选择的路,别选择好走的路,你才能拥有真正的自己。 🐼一、UDP协议特点 🐼二、UDP协议段格式详解 🐳今日良言:走好选择的路,别选择好走的路,你才能拥有真正的自…...

C#开发的OpenRA的NextPowerOf2
C#开发的OpenRA的NextPowerOf2 在游戏里,经常需要对计算资源进行优化。 比如屏幕的大小,以及缓冲区的大小,还有纹理的大小。 由于计算机都是基于二进制的原理,那么它的最快计算速度,就是让计算的数字都是2的n次方。 基于此策略,在程序里就需要计算出来最接近2的n次方的数…...
CDH 6.3.2启用HDFS高可用
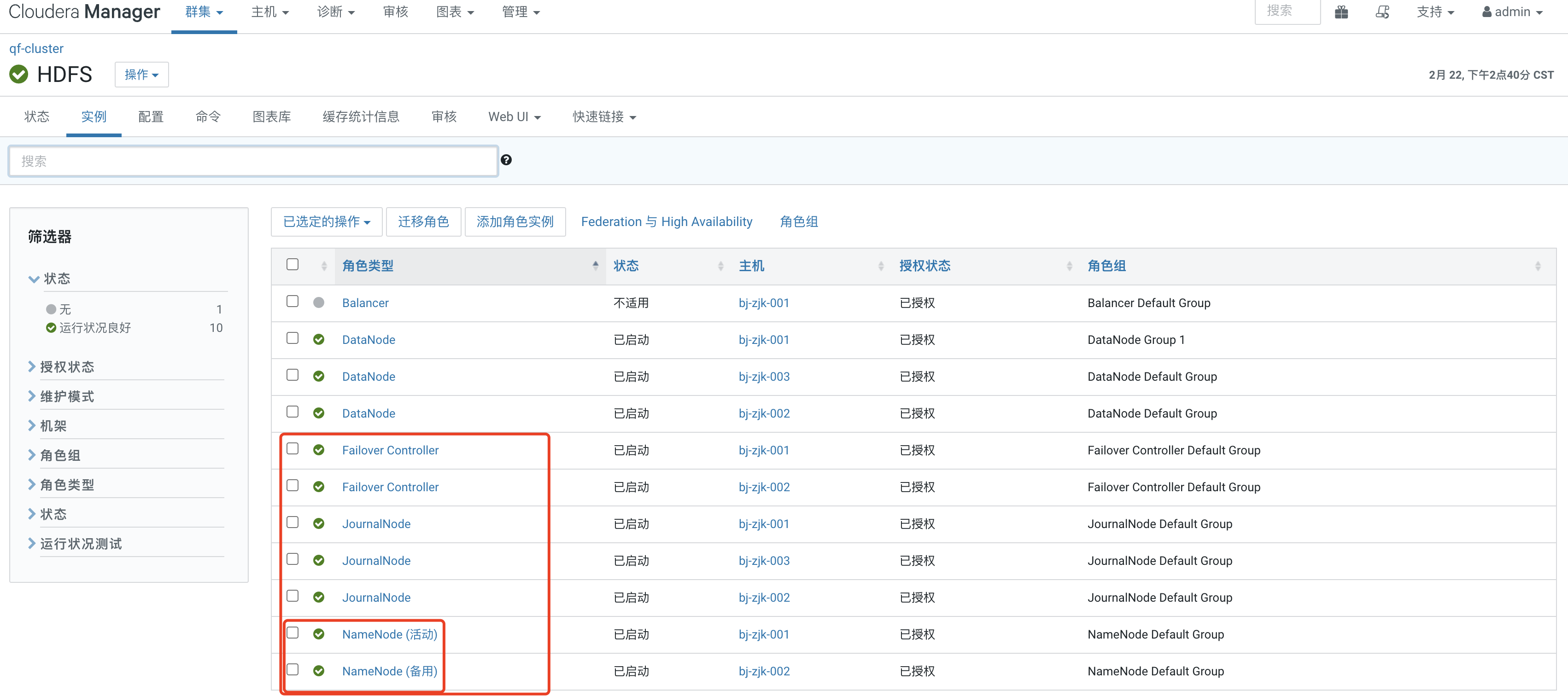
启用原因 CDH 6.3.2平台即将用于生产,生产平台几乎需要高可用平台,故需要升级CDH中的HDFS为HA。 启用准备 CDH已经成功安装并正常使用CMS的管理员账号正常登陆 HDFS启用HA 登陆CMS系统->选择HDFS服务->点击进入到HDFS服务详情页面,…...
多服务器节点访问解决一人一单问题+redis设置锁方案
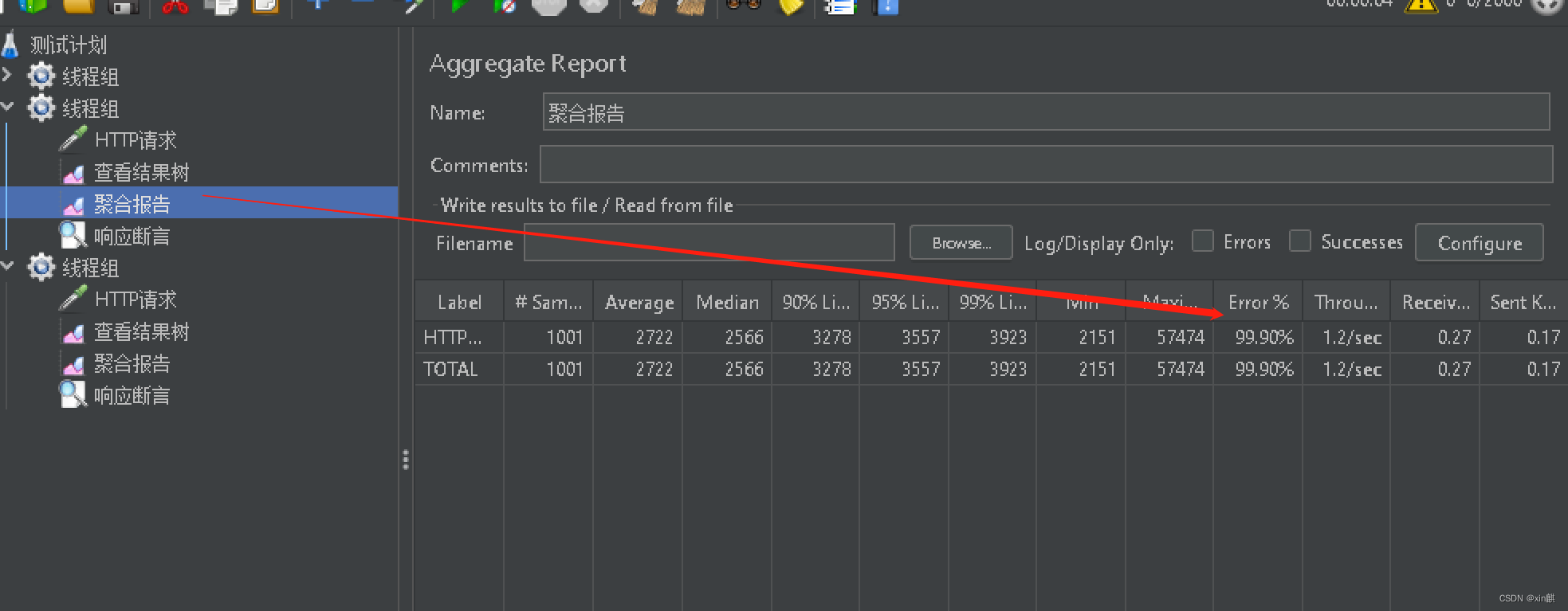
项目地址及项目具体介绍-码云仓库:https://gitee.com/flowers-bloom-is-the-sea/distributeNodeSolvePessimisticLockByRedis 测试1: 这里使用jmeter同时启动2各线程: 原来的数据库表的数据: goods的数据是: id …...

tensorflow 学习笔记(三):神经网络八股
本节内容: 前两节使用 Tensorflow2 的原生代码大叫神经网络。本节使用 keras 搭建神经网络(八股:六步法,有 Sequential 和 class 两种)。 文章目录一、搭建网络八股 sequential1.1、keras 介绍1.2、六步法搭建 keras …...
)
华为OD机试真题Python实现【射击比赛】真题+解题思路+代码(20222023)
射击比赛 题目 给定一个射击比赛成绩单 包含多个选手若干次射击的成绩分数 请对每个选手按其最高三个分数之和进行降序排名 输出降序排名后的选手 ID 序列 条件如下: 一个选手可以有多个射击成绩的分数 且次序不固定如果一个选手成绩小于三个 则认为选手的所有成绩无效 排名忽…...
(结论)(数学))
【YBT2023寒假Day12 C】树的计数 II(prufer)(结论)(数学)
树的计数 II 题目链接:YBT2023寒假Day12 C 题目大意 给你一个长度为 n 的排列 p,问你有多少个不同的有标号无根树,满足如果 i,j 有边那 pi,pj 也有边。 思路 首先可以把排列变成置换环。 注意到是树,发现一个置换中似乎不太可…...

深入浅出C++ ——多态
文章目录一、多态的概念二、多态的定义及实现1. 多态的构成条件2. 虚函数3. 虚函数的重写4. virtual的使用:5. 虚函数重写的两个例外:6. C11 override 和 final7. 重载、重写、重定义的对比三、抽象类四、多态的原理1. 虚函数表2. 多态的原理3. 静态绑定…...
)
华为OD机试真题Python实现【整数编码】真题+解题思路+代码(20222023)
整数编码 题目 实现一个整数编码方法 使得待编码的数字越小 编码后所占用的字节数越小 编码规则如下 编码时7位一组,每个字节的低 7 位用于存储待编码数字的补码字节的最高位表示后续是否还有字节,置1表示后面还有更多的字节,置0表示当前字节为最后一个字节采用小端序编码…...

FPGA纯Vhdl实现MIPI CSI2RX视频解码输出,OV13850采集,提供工程源码和技术支持
目录1、前言2、Xilinx官方主推的MIPI解码方案3、纯Vhdl方案解码MIPI4、vivado工程介绍5、上板调试验证6、福利:工程代码的获取1、前言 FPGA图像采集领域目前协议最复杂、技术难度最高的应该就是MIPI协议了,MIPI解码难度之高,令无数英雄竞折腰…...
7 个 JavaScript Web API 来构建你不知道的未来网站
随着技术的日新月异,为开发人员提供了令人难以置信的新工具和API。但据了解,在100 多个 API中,只有5%被开发人员积极使用。让我们来看看一些有用的Web API,它们可以帮助您将网站推向月球!🌕🚀1.…...

跟ChatGPT,聊聊ChatGPT
不仅“上知天文、下知地理”,似乎还能对答如流、出口成诗,甚至还能写剧本、编音乐、写代码——最近,一款名叫ChatGPT的人工智能聊天机器人火爆全球。由此,一系列关于新一代技术变革、人工智能替代人力、巨头企业扎堆入局AI的讨论在…...
)
Java 数组(详细教学 基础篇)
一、数组的基本要素 标识符:数组的名称数组元素:数组中存放的数据元素下标:对数组元素进行编号,数组下标从0开始来访问元素类型:数组元素的数据类型 二、数组的五种赋值方法和使用方法 声明数组 int[] arr;//开辟三个…...
)
python装饰器原理 | 常用装饰器使用(@cache, @lru_cache)
🚀 关于python的装饰器原理介绍可看这里,讲的挺简洁易懂:python装饰器原理 ⭐ 弄懂装饰器原理后,来学学常用装饰器。 文章目录1、cache, lru_cache1、cache, lru_cache 也就是一种装饰在被执行的函数上,将其执行的结果…...
[oeasy]python0090_极客起源_wozniac_苹果公司_Jobs_Wozniac
极客起源 回忆上次内容 上次回顾了 DEC公司的兴起 从IBM的大型机 到DEC的小型机Mini Computer 再到DEC的终端 VT-100 计算机基础元器件发生了进化 从ENIAC的 电子管到PDP系列的 晶体管 新的器件 体积小了价格低了稳定性 提高了而且 连成了网络 ARPA网 就是 最初的Internet …...
)
Spring基础总结(下)
简介 本章节通过手写一个简单的 Spring 框架来加深对 Spring 框架源码以及设计思想的理解; 实现步骤 BeanScope 枚举代码 public enum BeanScope { sigleton, prototype; }AppConfig 配置类 // 定义包扫描路径 ComponentScan("com.dufu.spring"…...

设计模式面试题
设计模式分为 创建型 工厂模式 单例 原型行为性 责任链 迭代器 命令中介型结构性 适配器 代理 门面 装饰器 组合 桥接单例设计模式 懒汉式 用到时再创建,省内存 饿汉式 类创建时就创建,会占用内存 内部类 用到时再创建,省内存 线程池、数据…...

需要知道的一些API接口的基础知识
API是应用程序编程接口(Application Programming Interface)的缩写,能够起到两个软件组件之间的连接器或中介的作用。此类接口往往通过一组明确的协议,来表示各种原始的请求和响应。API文档可以向开发人员展示请求和响应是如何形成…...

互融云数字资产管理平台综合解决方案
自十八大以来,发展数字经济逐步成为了国家战略。从2015年国务院印发《促进大数据发展行动纲要》,到2020年4月中央发布《关于构建更加完善的要素市场化配置体制机制的意见》,再到2022年底出台《中共中央、国务院关于构建数据基础制度更好发挥数…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
