python装饰器原理 | 常用装饰器使用(@cache, @lru_cache)
🚀 关于python的装饰器原理介绍可看这里,讲的挺简洁易懂:python装饰器原理
⭐ 弄懂装饰器原理后,来学学常用装饰器。
文章目录
- 1、@cache, @lru_cache
1、@cache, @lru_cache
也就是一种装饰在被执行的函数上,将其执行的结果缓存起来,当下次请求的时候,如果请求该函数的传参未变则直接返回缓存起来的结果而不再执行函数的一种缓存装饰器。
- Python 内置模块 functools 提供的高阶函数 @functools.cache 是简单轻量级无长度限制的函数缓存,这种缓存有时称为 “memoize”(记忆化)。它是 3.9 新版功能,是在 lru_cache 缓存基础上简化了的对无限长度缓存。
- 语法为 @functools.cache(user_function),创建一个查找函数参数的字典的简单包装器。 因为它不需要移出旧值,缓存大小没有限制,所以比带有大小限制的 lru_cache() 更小更快。这个 @cache 装饰器是 Python 3.9 版中的新功能,在此之前,您可以通过 @lru_cache(maxsize=None) 获得相同的效果。
- lru_cache有两个参数:maxsize、typed。maxsize:如果不指定传参则默认值为128,表示最多缓存128个返回结果,当达到了128个时,有新的结果要保存时,则会删除最旧的那个结果。如果maxsize传入为None则表示可以缓存无限个结果;typed默认为false,代表不区分数据类型,如果设置为True,则会区分传参类型进行缓存,例如f(3.0)和f(3)将被视为不一样的传参。如果typed为True,则将分别缓存不同类型的参数。
以下是 cache 的实现源码:
from functools import lru_cachedef cache(user_function, /):'Simple lightweight unbounded cache. Sometimes called "memoize".'return lru_cache(maxsize=None)(user_function)
看个例子来秒懂@cache的原理:
def test(a,b):print('开始计算a+b的值...')return a + b
print('1+2等于:', test(1, 2))
print('1+2等于:', test(1, 2))
# 开始计算a+b的值...
# 1+2等于: 3
# 开始计算a+b的值...
# 1+2等于: 3@lru_cache(maxsize=None) # 等价于@cache
def test(a,b):print('开始计算a+b的值...')return a + b
print('1+2等于:', test(1, 2))
print('1+2等于:', test(1, 2))
# 开始计算a+b的值...
# 1+2等于: 3
# 1+2等于: 3
⭐ 可以@cache可用在dfs记忆化场景中。
相关文章:
)
python装饰器原理 | 常用装饰器使用(@cache, @lru_cache)
🚀 关于python的装饰器原理介绍可看这里,讲的挺简洁易懂:python装饰器原理 ⭐ 弄懂装饰器原理后,来学学常用装饰器。 文章目录1、cache, lru_cache1、cache, lru_cache 也就是一种装饰在被执行的函数上,将其执行的结果…...
[oeasy]python0090_极客起源_wozniac_苹果公司_Jobs_Wozniac
极客起源 回忆上次内容 上次回顾了 DEC公司的兴起 从IBM的大型机 到DEC的小型机Mini Computer 再到DEC的终端 VT-100 计算机基础元器件发生了进化 从ENIAC的 电子管到PDP系列的 晶体管 新的器件 体积小了价格低了稳定性 提高了而且 连成了网络 ARPA网 就是 最初的Internet …...
)
Spring基础总结(下)
简介 本章节通过手写一个简单的 Spring 框架来加深对 Spring 框架源码以及设计思想的理解; 实现步骤 BeanScope 枚举代码 public enum BeanScope { sigleton, prototype; }AppConfig 配置类 // 定义包扫描路径 ComponentScan("com.dufu.spring"…...

设计模式面试题
设计模式分为 创建型 工厂模式 单例 原型行为性 责任链 迭代器 命令中介型结构性 适配器 代理 门面 装饰器 组合 桥接单例设计模式 懒汉式 用到时再创建,省内存 饿汉式 类创建时就创建,会占用内存 内部类 用到时再创建,省内存 线程池、数据…...

需要知道的一些API接口的基础知识
API是应用程序编程接口(Application Programming Interface)的缩写,能够起到两个软件组件之间的连接器或中介的作用。此类接口往往通过一组明确的协议,来表示各种原始的请求和响应。API文档可以向开发人员展示请求和响应是如何形成…...

互融云数字资产管理平台综合解决方案
自十八大以来,发展数字经济逐步成为了国家战略。从2015年国务院印发《促进大数据发展行动纲要》,到2020年4月中央发布《关于构建更加完善的要素市场化配置体制机制的意见》,再到2022年底出台《中共中央、国务院关于构建数据基础制度更好发挥数…...

记住这12个要点,你也能打造出让HR和技术主管前一亮的前端简历
第一篇章:吸引HR 如果你想在众多简历中脱颖而出,需要注意以下几点: 1、突出你的亮点: 给你的简历一个吸引人的文件命名和头部,突出你的关键技能和经验。 2、采用简洁的语言: 用简单易懂的语言来描述你的…...
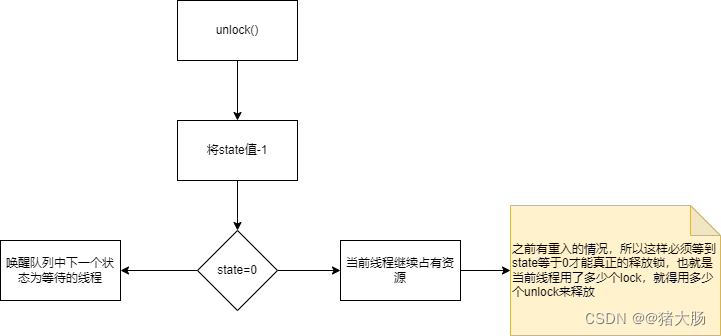
AQS学习:ReentrantLock源码解析
前言 多线程知识中理解了ReentrantLock之后,对于整个AQS也会有大概的理解,后面再去看其它锁的源码就会比较容易。下面带大家一块来学习ReentrantLock源码。 概述 ReentrantLock是可重入的互斥锁,虽然具有与synchronized相同功能࿰…...

RocketMQ源码分析消息消费机制—-消费端消息负载均衡机制与重新分布
1、消息消费需要解决的问题 首先再次重复啰嗦一下 RocketMQ 消息消费的一些基本元素的关系 主题 —》 消息队列(MessageQueue) 1 对多。 主题 —》 消息生产者,一般主题会由多个生产者组成,生产者组。 主题 —》 消息消费者,一般一个主题…...
)
华为OD机试真题Python实现【数据分类】真题+解题思路+代码(20222023)
数据分类 题目 对一个数据a进行分类, 分类方法是,此数据a(4 个字节大小)的 4 个字节相加对一个给定值b取模, 如果得到的结果小于一个给定的值c则数据a为有效类型,其类型为取模的值。 如果得到的结果大于或者等于c则数据a为无效类型。 比如一个数据a = 0x01010101,b = 3…...
vue项目中引入字体包
问题: 项目开发过程中,因UI的显示要求,需要引入一些字体,那如何引入外部字体呢?很简单,只需要以下3步 一 下载对应的字体包文件,放置到我们的项目中 比如我需要PingFangSC的系列字体&#…...
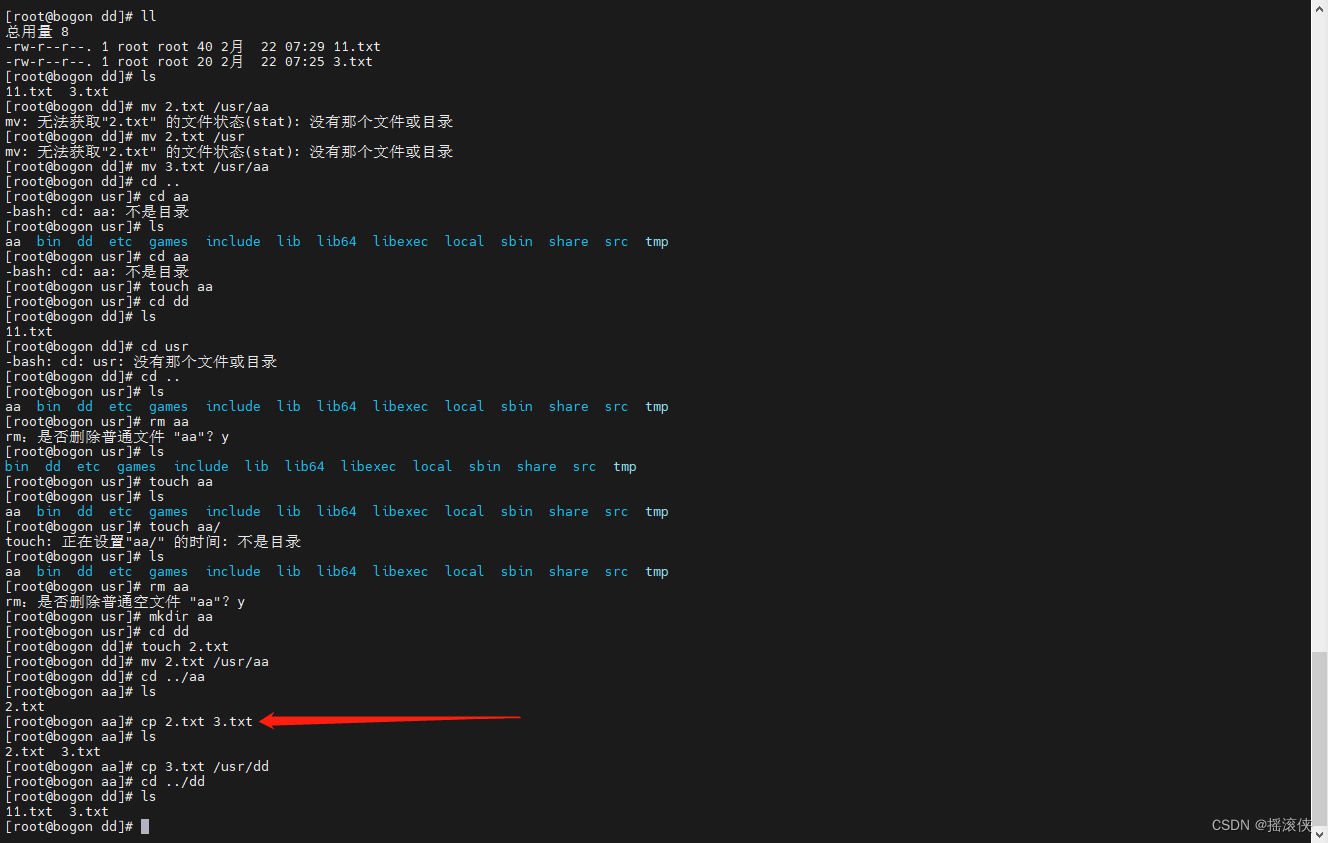
Linux 文件相关操作
文件相关操作 编辑文件 命令: vi 文件名 然后输入i进入编辑模式 编辑完成后输入esc退出编辑 输入:wq保存即便目录下没有这个文件,也可以想使用vi 文件名进行编辑,保存退出后会创建这个文件 查看文件内容 命令: cat 文件名复…...

【计算机网络】应用题方法总结
0.前言本篇博客主要记录自己在学习到的部分解决计算机网络应用题方法,主要参考视频如下:计算机网络期末复习 应用题_哔哩哔哩_bilibili【计算机网络】子网划分题型总结_哔哩哔哩_bilibili循环冗余码step 1:确定冗余码长度。多项式最高位即为冗…...
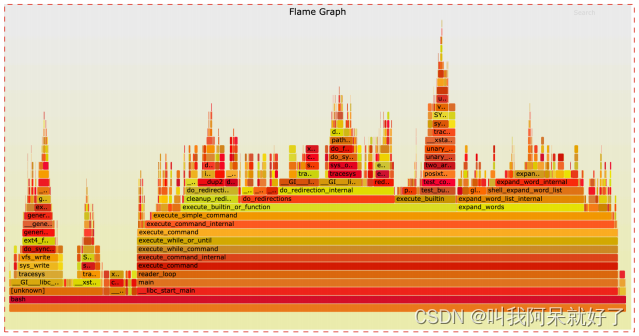
Linux 浅谈之性能分析工具 perf
Linux 浅谈之性能分析工具 perf HELLO,各位博友好,我是阿呆 🙈🙈🙈 这里是 Linux 浅谈系列,收录在操作系统专栏中 😜😜😜 本系列将记录一些阿呆个人整理的 OS 相关知识…...

代码随想录-Day7:四数相加、三数之和
454. 四数相加 II 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < nnums1[i] nums2[j] nums3[k] nums4[l] 0示例 1: 输入࿱…...
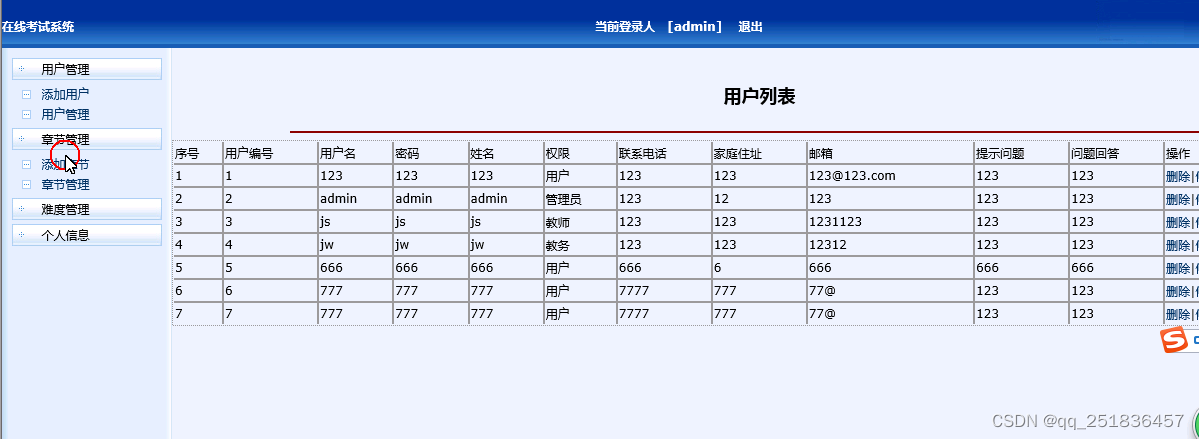
jsp在线考试系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 jsp 在线考试系统 是一套完善的web设计系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为TOMCAT7.0,Myeclipse8.5 开发,数据库为Mysql,使用j…...

【总结】2023数学建模美赛!收官!
今年的美赛时间是2.17-2.21,这学期疫情放开了之后管的没那么严了,我们小组就都提前一天到学校了,全力准备17号的比赛。 时间流程 刚拿到6个题的时候,我们三个人一人看两个题,每个人从两个题中再选出来一个自己觉得有…...

C# GDI+ winform绘图知识总结
一、Graphics GDI是GDI(Windows Graphics Device Interface)的后继者,它是.NET Framework为操作图形提供的应用程序编程接口,主要用在窗体上绘制各种图形图像,可以用于绘制各种数据图像、数学仿真等。 Graphics类是G…...
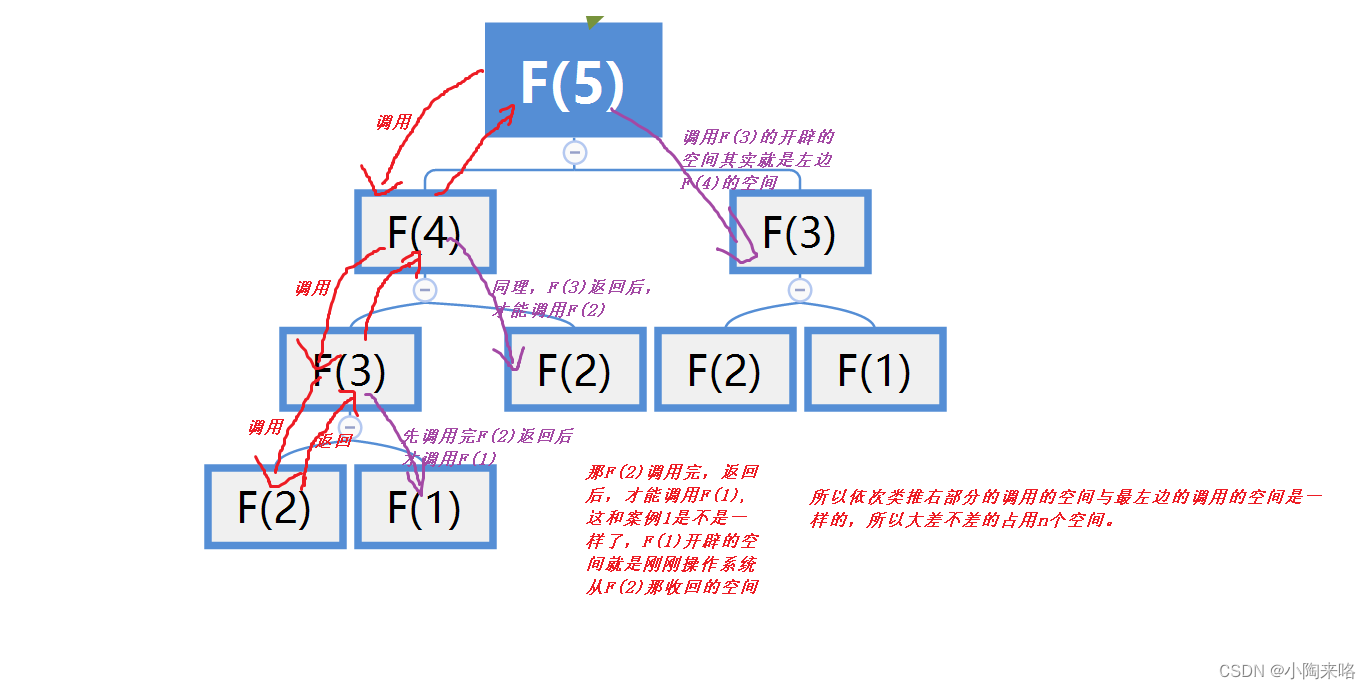
【研究空间复用及函数调用问题】
本篇总结函数调用过程会存在的一些奇怪现象,空间复用问题,其实本质上涉及函数调用的底层原理,理解函数栈帧的创建和销毁这样的问题直接迎刃而解。1.空间复用问题案例1案例22.函数调用过程不清晰问题案例33.总结1.空间复用问题 案例1 我们先…...
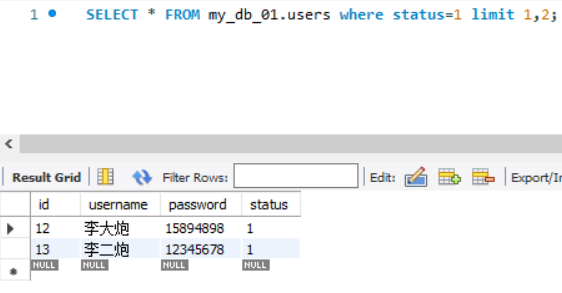
SQL常用查询语句
SELECT语句用于查询数据库中的内容 目录 1 查询指定表的所有内容 2 显示所有行的指定列 3 显示指定行的指定列 4 对查询结果进行排序 4.1 按照单一字段排序 4.2 多重排序 5 查询数据总数 5.1 查询一共有多少行 5.2 统计符合条件的有多少行 6 给查询出来的…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
