【研究空间复用及函数调用问题】
本篇总结函数调用过程会存在的一些奇怪现象,空间复用问题,其实本质上涉及函数调用的底层原理,理解函数栈帧的创建和销毁这样的问题直接迎刃而解。
- 1.空间复用问题
- 案例1
- 案例2
- 2.函数调用过程不清晰问题
- 案例3
- 3.总结
1.空间复用问题
案例1
我们先来看一个代码:
void F1()
{int a = 10;printf("%p\n", &a);
}
void F2()
{int b = 10;printf("%p\n", &b);
}
int main()
{F1();F2();return 0;
}
F1和F2函数的操作基本一样,你说它们所开辟的空间的地址是同一块吗?
或者说,a和b的地址是一样的吗?
结果是:一样的。为什么呢?
我们知道调用函数需要给函数开辟栈帧,也就是开辟空间,而栈帧是在堆区开辟的
当函数使用完后,该函数栈帧就要销毁。
但不是真正意义上的销毁,而是把使用该空间的权限还给操作系统,这片区域不再受你操控。
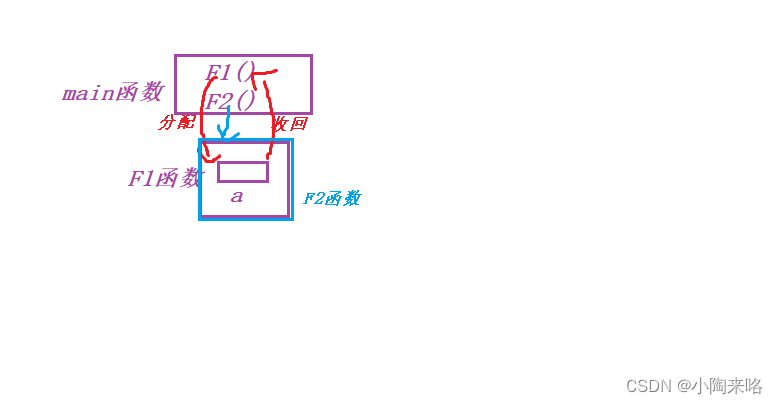
所以我们在调用F1()函数时,操作系统先给F1()开辟栈帧,给变量a分配内存。然后当F1()函数结束时,该空间又被操作系统收回
接着又调用F2()函数,操作系统又将刚刚收回的空间又分配给F2()函数。
所以F1函数和F2函数使用的空间地址是一样的,变量a和变量b的地址也就是一样的。
案例2
这是一个阶乘递归的代码
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}
int main()
{long long n;Fac(n);return 0;
}
请问它的空间复杂度和时间复杂度是多少呢?
函数Fac每次调用都会返回Fac(n-1)*n,直到N==0时才返回1.
也就是递归了n次,所以时间复杂度为O(n).
而空间复杂度呢?
因为Fac函数每次调用自己都会开辟一个函数栈帧,调用了n次,所以开辟了n个空间。
所以空间复杂度也是O(n).
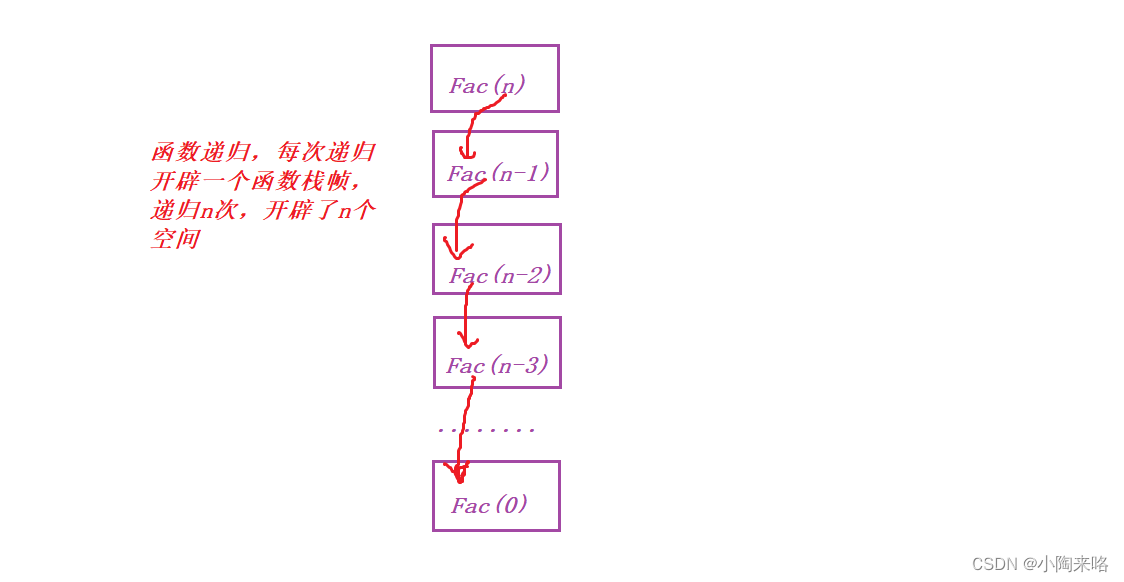
那想一下,Fac(n)与Fac(n-1)与Fac(n-2)…等函数的空间地址是同一块空间吗?
综合上面的案例我们应该判断它们不是同一块空间的。
为什么呢?
上面的案例是F1函数调用完,结束后,再调用的F2函数
而阶乘递归是属于嵌套调用,每个函数都还没完全结束就又调用另一个函数了,所以它们开辟的空间肯定不一样,它们各自使用的空间都没有被操作系统收回过,怎么可能有其他函数又去占用这块空间呢。
而对案例修改一下,也可以让F1和F2函数的地址不一样,也就是在F1函数的内部去调用函数F2,这样它们的空间就不会重复了。
如下所示:
void F1()
{int a = 10;printf("%p\n", &a);F2();
}
void F2()
{int b = 10;printf("%p\n", &b);
}
int main()
{F1();return 0;
}
2.函数调用过程不清晰问题
案例3
这是一个斐波那契契递归Fib
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
int main()
{long long n;Fib(n);return 0;
}
你知道这个递归Fib函数的空间复杂度和时间复杂度吗?
Fib(n)函数每次返回两个函数Fib(n-1)+Fib(n-2).直到n<3时返回1.
也就是Fib函数每次调用都会又调用两个函数,而这个两个函数相当于又调用4个函数依次类推…最后应该调用2^n次
所以时间复杂度为O(2^n).
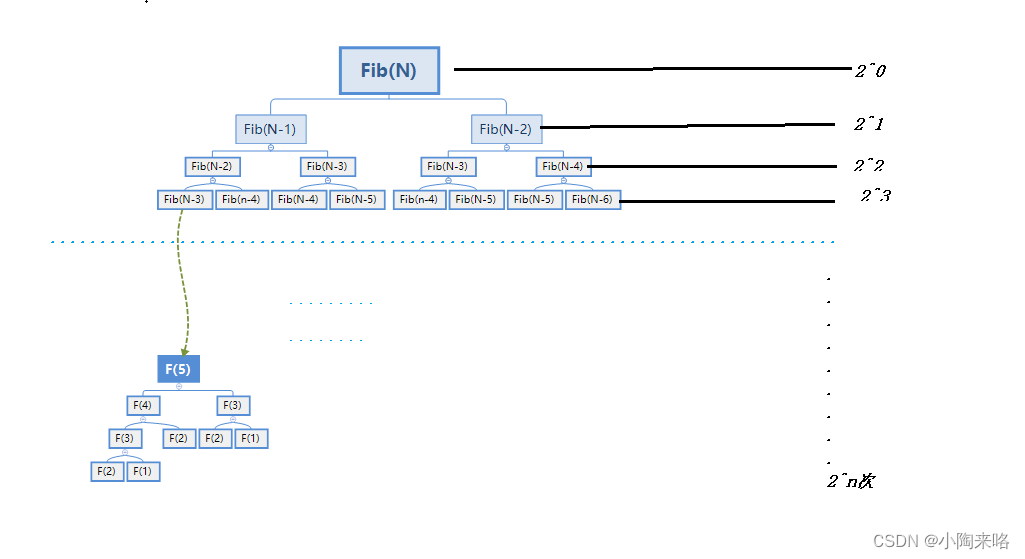
那空间复杂度呢?空间复杂度是多少呢?
有的人可能想呀,它不是相当于调用了2 ^ n次嘛,那不就是申请了2 ^ n个空间吗。真的是这样吗?
可能现在还有很多人没有搞清楚函数是怎么调用的,递归是怎么调用的。
有的人可能想是Fib(n)调用Fib(n-1)和Fib(n-2),然后操作系统就给Fib(n-1)和Fib(n-2)分配栈帧了,但其实不是。
函数的调用只有完全调用完才能去执行下一步。
调用Fib(n-1)后,其实会继续往下面调用Fib(n-2),然后再往下调用Fib(n-3)直到调用到Fib(2),Fib(2)返回1后,Fib(2)也就结束,函数栈帧销毁,回到F(3),F(3)这时才开始调用F(1),F(1)返回1,F(1)的栈帧销毁,返回F(3),F(2)又开始调用了。依次类推
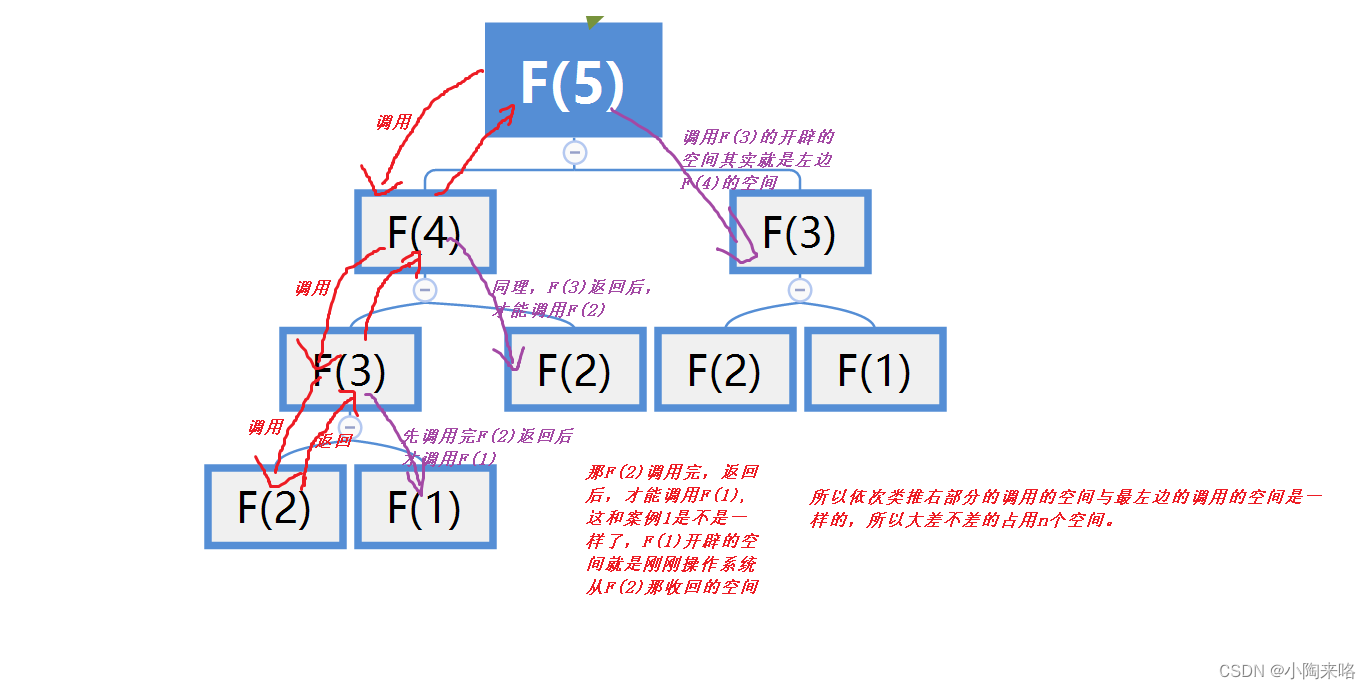
Fib(2)返回后,操作系统是不是就将它的空间回收了,然后又调用了Fib(1)所以Fib(1)开辟的空间就是刚刚操作系统收回的空间呀。
其实就是左边Fib(2)和右边F(1)用的是同一块空间。依次类推,Fib(4)返回后,空间被收回,然后操作系统又将空间分配给右边的Fib(3)使用。所以大体上左边和右边是共用一块空间,而左边是调用了n个空间,所以最后的空间大小是O(n).
3.总结
这三个个案例本质上就是要搞清楚函数栈帧是如何创建的以及如何销毁的。
搞清楚函数是如何调用的,调用前操作系统要给函数分配栈帧,调用函数结束后,操作系统要将栈帧收回。
如果对函数栈帧方面有兴趣的可以阅读一下博主的《细谈函数栈帧的创建与销毁》。
还有我们可以发现:
时间是一去不复返的,不可再重复利用。
而空间是可以重复利用的。所以我们要特别重视算法的时间效率。
相关文章:

【研究空间复用及函数调用问题】
本篇总结函数调用过程会存在的一些奇怪现象,空间复用问题,其实本质上涉及函数调用的底层原理,理解函数栈帧的创建和销毁这样的问题直接迎刃而解。1.空间复用问题案例1案例22.函数调用过程不清晰问题案例33.总结1.空间复用问题 案例1 我们先…...
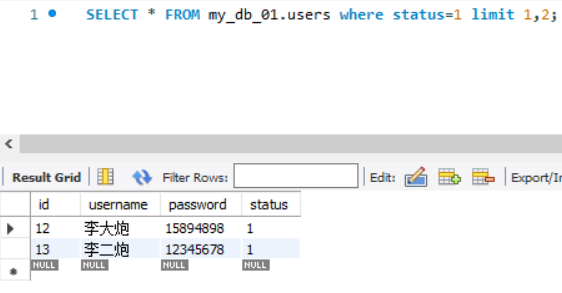
SQL常用查询语句
SELECT语句用于查询数据库中的内容 目录 1 查询指定表的所有内容 2 显示所有行的指定列 3 显示指定行的指定列 4 对查询结果进行排序 4.1 按照单一字段排序 4.2 多重排序 5 查询数据总数 5.1 查询一共有多少行 5.2 统计符合条件的有多少行 6 给查询出来的…...

【Python实战】一大波高颜值主播来袭:快看,某网站颜值排名,为了这个排名我可是大费周章啦,第一名不亏是你...(人脸检测+爬虫实战)
导语 民间一直有个传闻......「听说某站的小哥哥小姐姐颜值都很高哦!」 (不是颜值高才能加入,是优秀的人恰好颜值高) 所有文章完整的素材源码都在👇👇 粉丝白嫖源码福利,请移步至CSDN社区或文末…...

Linux进程学习【三】
✨个人主页: Yohifo 🎉所属专栏: Linux学习之旅 🎊每篇一句: 图片来源 🎃操作环境: CentOS 7.6 阿里云远程服务器 Perseverance is not a long race; it is many short races one after another…...
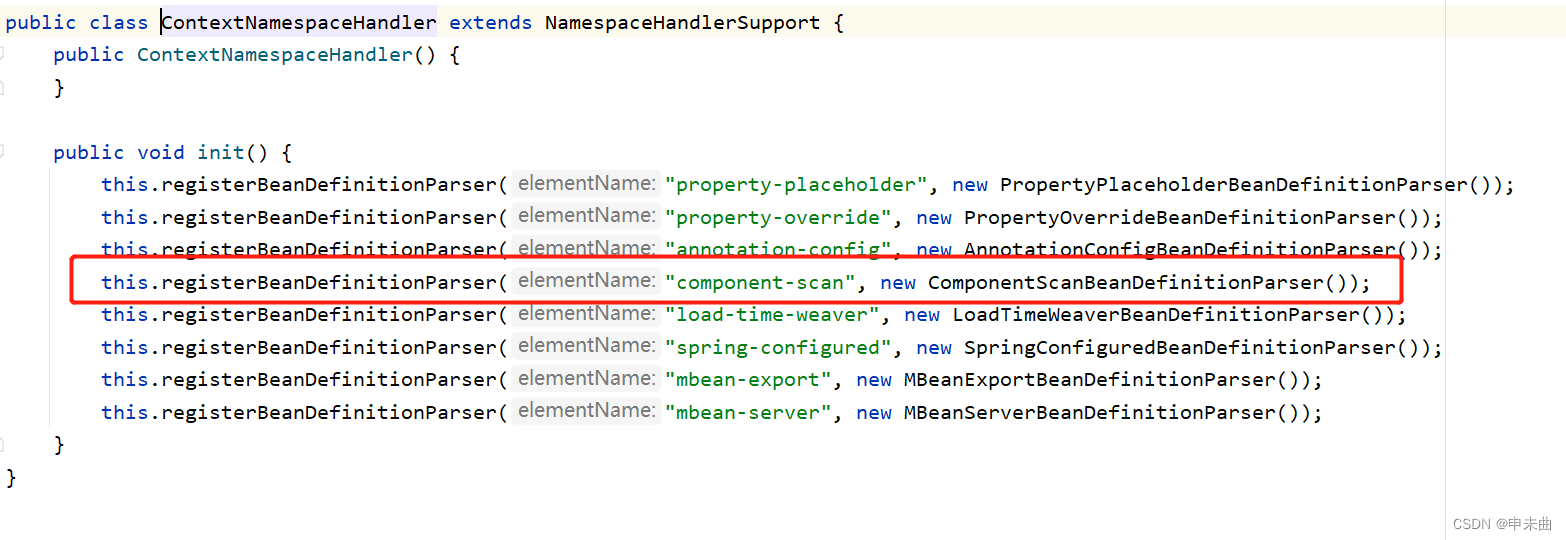
Spring自动装配的底层逻辑
Spring是如何自动装配Bean的?看源码一些自己的理解,如有错漏,请指正 使用Spring之前我们要先去web.xml中设置一下Spring的配置文件,在Spring的配置文件中,是通过component-scan扫描器去扫描base-package底下所有的类装…...

华为OD机试 - 数组合并(C++) | 附带编码思路 【2023】
刷算法题之前必看 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:https://blog.csdn.net/hihell/category_12199283.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 华为OD机试题…...
在vue3+ts的项目中,如何解决vant组件自带表单校验不生效?
问题描述: 点击发送验证码后,为了让逻辑更加严谨,使用了vant组件自带的表单校验,进行二次校验,防止验证码发送成功后,登录手机号被二次修改,但根据官网描述cv之后不生效,甚至连获取…...
)
华为OD机试真题Python实现【子序列长度】真题+解题思路+代码(20222023)
子序列长度 题目 有 N 个正整数组成的一个序列 给定一个整数sum 求长度最长的的连续子序列使他们的和等于sum 返回次子序列的长度 如果没有满足要求的序列 返回-1 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 ## 输入 两行输入 第一行…...

【答疑现场】我一个搞嵌入式的,有必要学习Python吗?
【答疑现场】我一个搞嵌入式的,有必要学习Python吗? 文章目录1 写在前面2 一个结论3 Python在嵌入式领域能干啥事4 Python是用来干大事的5 友情推荐6 福利活动大家好,我是架构师李肯,一个专注于嵌入式物联网系统架构设计的攻城狮。…...

MySQL存表报错问题 Incorrect string value
MySQL存表报错问题 Incorrect string value 问题 Incorrect string value: ‘\xF0\xA8\xA5\xA5\xE5\xAD…’ for column ‘xxxxxxx’ at row 1 意思是错误的字符,常出现在添加中文字符的时候。这个问题的产生原因主要是因为一些特色中文字符或者Emoji表情占4个字…...

SAP ABAP DIALOG长文本编辑框
1. 在SCREEN100 中创建一个定制控制(容器),命名为PP *&---------------------------------------------------------------------* *& Report ZTEST_TEXT *& *&---------------------------------------------------------------------* *& *…...
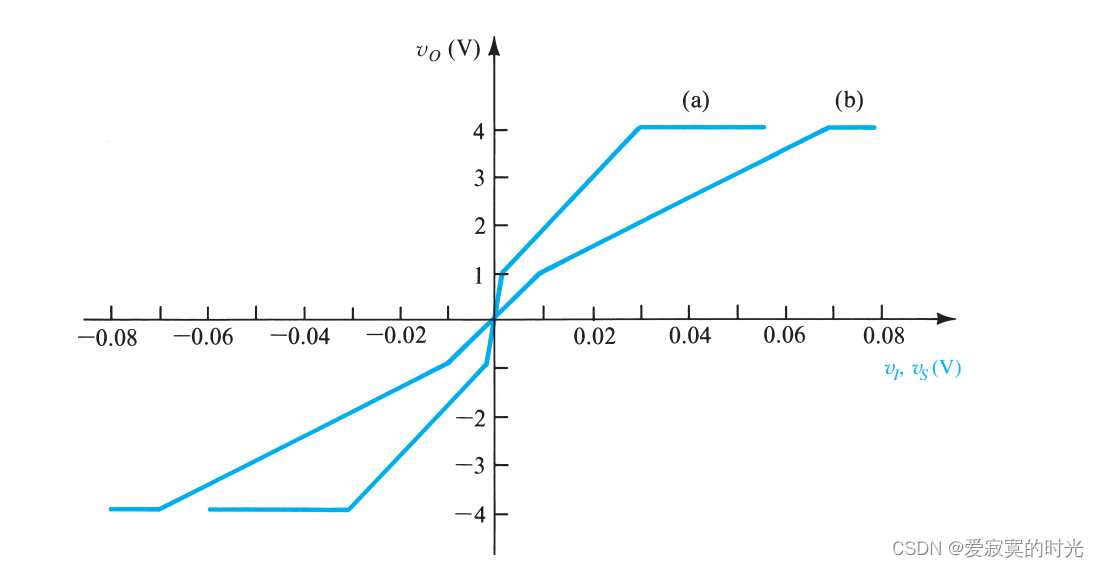
电子技术——负反馈特性
电子技术——负反馈特性 本节我们进一步深入介绍负反馈特性。 增益脱敏性 假设 β\betaβ 是一个常数。考虑下面的微分方程: dAfdA(1Aβ)2dA_f \frac{dA}{(1 A\beta)^2} dAf(1Aβ)2dA 将上式除以 AfA1AβA_f \frac{A}{1A\beta}Af1AβA 得到࿱…...

网站移动端性能优化方法
移动端优化 click 的 300ms 延迟响应 click 的 300ms 延迟是由双击缩放(double tap to zoom)所导致的,由于用户可以进行双击缩放或者双击滚动的操作,当用户一次点击屏幕之后,浏览器并不能立刻判断用户是确实要打开这个链接,还是想要进行双击操作。因此,移动端浏览器就等…...

2023年AI语音会议汇总
2023年,AI语音领域学术会议精彩纷呈,语音之家汇总了国内外重要的会议呈现给大家,大家可根据时间统筹安排好2023年的学术活动交流行程。如果信息有误,欢迎指正。 ICASSP 2023 2023 IEEE International Conference on Acoustics, S…...

Mybatis持久层框架 | Mapper加载方式、目录结构解析
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! Mapper(resource、class、package)加载方式 resource方式加载 通过resource或url加载单个mapper,接口文件与映射文件不在同一路径下,只能用re…...

九龙证券|创业板向未盈利企业敞开大门 考验投行估值定价能力
未盈余企业上市有了新选择。2月17日,全面实行股票发行注册制相关准则规矩发布施行。深交所发布《深圳证券交易所创业板股票上市规矩(2023年修订)》及《关于未盈余企业在创业板上市相关事宜的告诉》,“预计市值不低于50亿元&#x…...
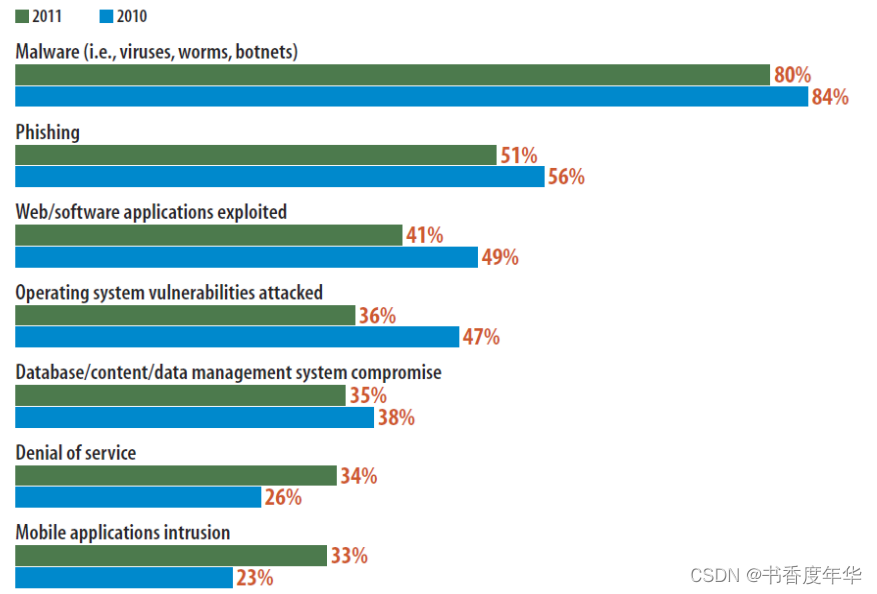
「TCG 规范解读」第12章 TPM工作组 TCG身份验证研讨
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...
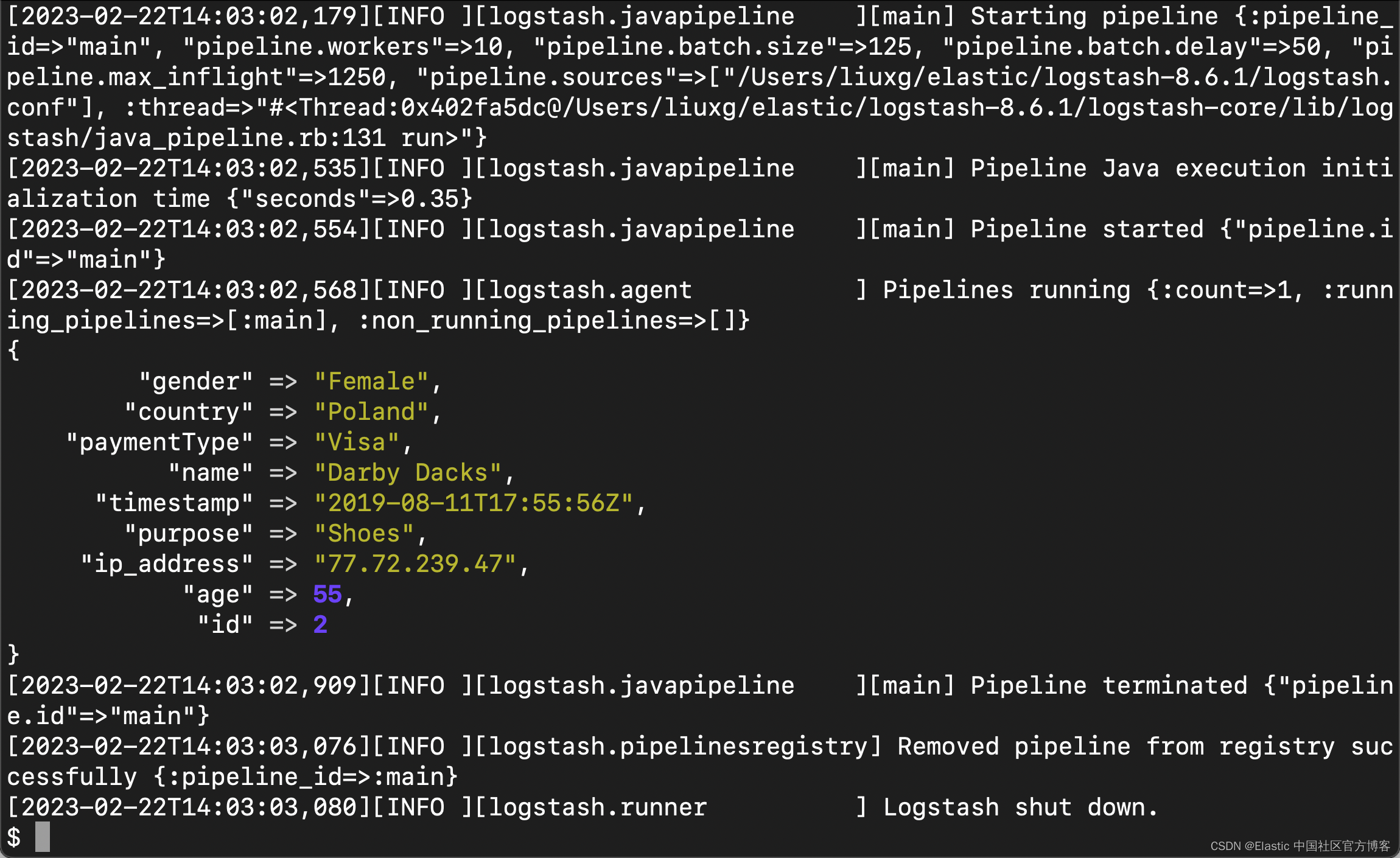
Logstash:在 Logstash 管道中的定制的 Elasticsearch update by query
我们知道 Elasticsearch output plugin 为我们在 Logstash 的 pipeline 中向 Elasticsearch 的写入提供了可能。我们可以使用如下的格式向 Elasticsearch 写入数据: elasticsearch {hosts > ["https://localhost:9200"]index > "data-%{YYYY.M…...

Spring Cloud Kubernetes环境下使用Jasypt
前言最近半年着手开始做了基于微服务的中台项目,整个项目的技术栈采用的是Java Spring Cloud Kubernetes Istio。业务开放上还是相当顺利的。但是在安全审核上,运维组提出了一个简易。现在项目一些敏感配置,例如MySQL用户的密码࿰…...
Kotlin-面向对象
本片博客主要写创建对象,创建接口,创建抽象类,data关键字的作用 创建对象 如何声明一个对象,使用class关键字 格式为: class 对象名字(对象属性名:属性类型…){} 如果对象没有函数…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
