Python3 集合
Python3 集合
集合(set)是一个无序的不重复元素序列。
可以使用大括号 { } 或者 set() 函数创建集合,注意:创建一个空集合必须用 set() 而不是 { },因为 { } 是用来创建一个空字典。
创建格式:
parame = {value01,value02,...}
或者
set(value)
实例(Python 3.0+)
>>> basket = {'apple', 'orange', 'apple', 'pear', 'orange', 'banana'}
>>> print(basket) # 这里演示的是去重功能
{'orange', 'banana', 'pear', 'apple'}
>>> 'orange' in basket # 快速判断元素是否在集合内
True
>>> 'crabgrass' in basket
False
>>> # 下面展示两个集合间的运算.
...
>>> a = set('abracadabra')
>>> b = set('alacazam')
>>> a
{'a', 'r', 'b', 'c', 'd'}
>>> a - b # 集合a中包含而集合b中不包含的元素
{'r', 'd', 'b'}
>>> a | b # 集合a或b中包含的所有元素
{'a', 'c', 'r', 'd', 'b', 'm', 'z', 'l'}
>>> a & b # 集合a和b中都包含了的元素
{'a', 'c'}
>>> a ^ b # 不同时包含于a和b的元素
{'r', 'd', 'b', 'm', 'z', 'l'}
类似列表推导式,同样集合支持集合推导式(Set comprehension):
实例(Python 3.0+)
>>> a = {x for x in 'abracadabra' if x not in 'abc'}
>>> a
{'r', 'd'}
集合的基本操作
1、添加元素
语法格式如下:
s.add( x )
将元素 x 添加到集合 s 中,如果元素已存在,则不进行任何操作。
实例(Python 3.0+)
>>> thisset = set(("Google", "Runoob", "Taobao"))
>>> thisset.add("Facebook")
>>> print(thisset)
{'Taobao', 'Facebook', 'Google', 'Runoob'}
还有一个方法,也可以添加元素,且参数可以是列表,元组,字典等,语法格式如下:
s.update( x )
x 可以有多个,用逗号分开。
实例(Python 3.0+)
>>> thisset = set(("Google", "Runoob", "Taobao"))
>>> thisset.update({1,3})
>>> print(thisset)
{1, 3, 'Google', 'Taobao', 'Runoob'}
>>> thisset.update([1,4],[5,6])
>>> print(thisset)
{1, 3, 4, 5, 6, 'Google', 'Taobao', 'Runoob'}
>>>
2、移除元素
语法格式如下:
s.remove( x )
将元素 x 从集合 s 中移除,如果元素不存在,则会发生错误。
实例(Python 3.0+)
>>> thisset = set(("Google", "Runoob", "Taobao"))
>>> thisset.remove("Taobao")
>>> print(thisset)
{'Google', 'Runoob'}
>>> thisset.remove("Facebook") # 不存在会发生错误
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
KeyError: 'Facebook'
>>>
此外还有一个方法也是移除集合中的元素,且如果元素不存在,不会发生错误。格式如下所示:
s.discard( x )
实例(Python 3.0+)
>>> thisset = set(("Google", "Runoob", "Taobao"))
>>> thisset.discard("Facebook") # 不存在不会发生错误
>>> print(thisset)
{'Taobao', 'Google', 'Runoob'}
我们也可以设置随机删除集合中的一个元素,语法格式如下:
s.pop()
脚本模式实例(Python 3.0+)
thisset = set(("Google", "Runoob", "Taobao", "Facebook"))
x = thisset.pop()
print(x)
输出结果:
$ python3 test.py Runoob
多次执行测试结果都不一样。
set 集合的 pop 方法会对集合进行无序的排列,然后将这个无序排列集合的左面第一个元素进行删除。
3、计算集合元素个数
语法格式如下:
len(s)
计算集合 s 元素个数。
实例(Python 3.0+)
>>> thisset = set(("Google", "Runoob", "Taobao"))
>>> len(thisset)
3
4、清空集合
语法格式如下:
s.clear()
清空集合 s。
实例(Python 3.0+)
>>> thisset = set(("Google", "Runoob", "Taobao"))
>>> thisset.clear()
>>> print(thisset)
set()
5、判断元素是否在集合中存在
语法格式如下:
x in s
判断元素 x 是否在集合 s 中,存在返回 True,不存在返回 False。
实例(Python 3.0+)
>>> thisset = set(("Google", "Runoob", "Taobao"))
>>> "Runoob" in thisset
True
>>> "Facebook" in thisset
False
>>>
集合内置方法完整列表
| 方法 | 描述 |
|---|---|
| add() | 为集合添加元素 |
| clear() | 移除集合中的所有元素 |
| copy() | 拷贝一个集合 |
| difference() | 返回多个集合的差集 |
| difference_update() | 移除集合中的元素,该元素在指定的集合也存在。 |
| discard() | 删除集合中指定的元素 |
| intersection() | 返回集合的交集 |
| intersection_update() | 返回集合的交集。 |
| isdisjoint() | 判断两个集合是否包含相同的元素,如果没有返回 True,否则返回 False。 |
| issubset() | 判断指定集合是否为该方法参数集合的子集。 |
| issuperset() | 判断该方法的参数集合是否为指定集合的子集 |
| pop() | 随机移除元素 |
| remove() | 移除指定元素 |
| symmetric_difference() | 返回两个集合中不重复的元素集合。 |
| symmetric_difference_update() | 移除当前集合中在另外一个指定集合相同的元素,并将另外一个指定集合中不同的元素插入到当前集合中。 |
| union() | 返回两个集合的并集 |
| update() | 给集合添加元素 |
相关文章:

Python3 集合
Python3 集合 集合(set)是一个无序的不重复元素序列。 可以使用大括号 { } 或者 set() 函数创建集合,注意:创建一个空集合必须用 set() 而不是 { },因为 { } 是用来创建一个空字典。 创建格式: parame …...

【山河送书第十期】:《Python 自动化办公应用大全》参与活动,送书两本!!
【山河送书第十期】:《Python 自动化办公应用大全》参与活动,送书两本!! 前言一书籍亮点二作者简介三内容简介四购买链接五参与方式六往期赠书回顾 前言 在过去的 5 年里,Python 已经 3 次获得 TIOBE 指数年度大奖&am…...

Java多线程——同步
同步是什么? 当两个线程同时对一个变量进行修改时,不同的访问顺序会造成不一样的结果,这时候就需要同步保证结果的唯一性。 未同步时 新建Bank类,transfer()用于在两个账户之间转账金额 class Bank {private double[] account…...
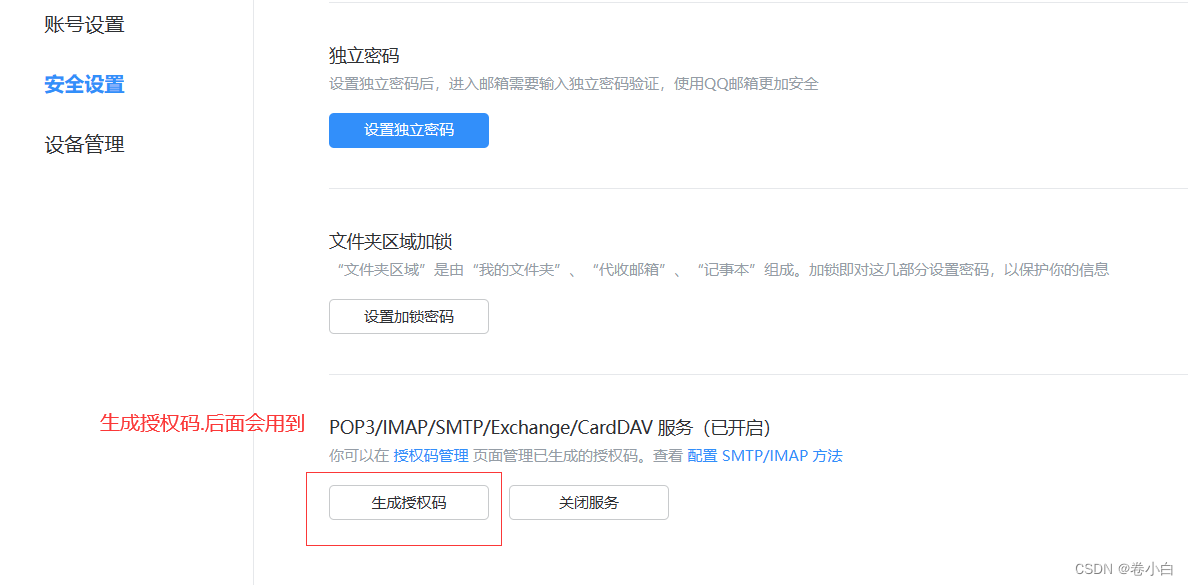
Vue+NodeJS实现邮件发送
一.邮箱配置 这里以QQ邮箱为例,网易邮箱类似. 设置->账号 二.后端服务搭建 index.js const express require(express) const router require(./router); const app express()// 使用路由文件 app.use(/,router);app.listen(3000, () > {console.log(server…...
TCP粘包)
Go语言网络编程(socket编程)TCP粘包
1、TCP粘包 服务端代码如下: // socket_stick/server/main.gofunc process(conn net.Conn) {defer conn.Close()reader : bufio.NewReader(conn)var buf [1024]bytefor {n, err : reader.Read(buf[:])if err io.EOF {break}if err ! nil {fmt.Println("read…...
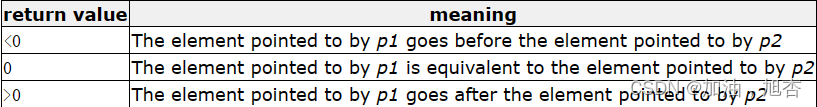
【再识C进阶2(中)】详细介绍指针的进阶——函数指针数组、回调函数、qsort函数
前言 💓作者简介: 加油,旭杏,目前大二,正在学习C,数据结构等👀 💓作者主页:加油,旭杏的主页👀 ⏩本文收录在:再识C进阶的专栏…...
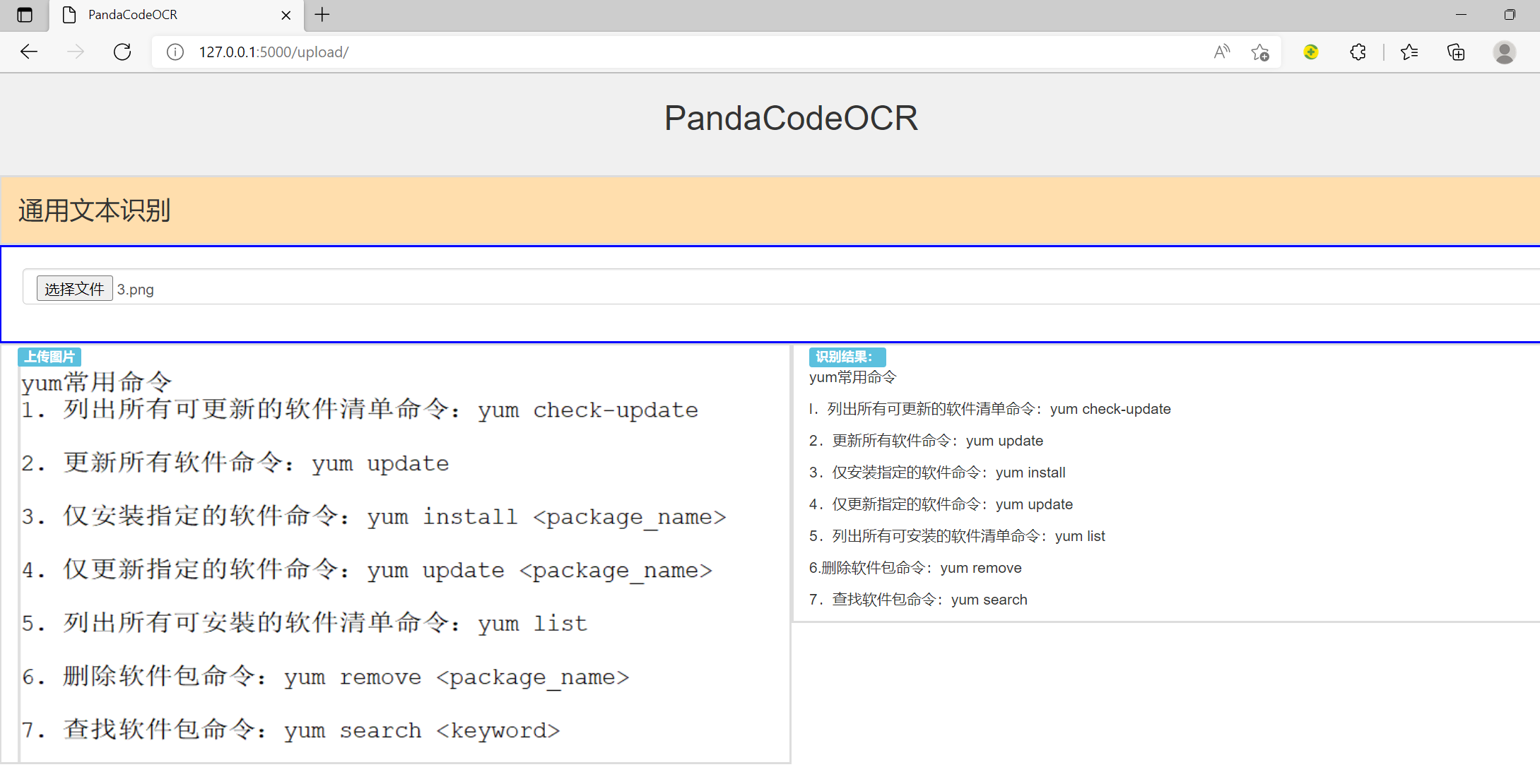
PaddleOCR学习笔记3-通用识别服务
今天优化了下之前的初步识别服务的python代码和html代码。 采用flask paddleocr bootstrap快速搭建OCR识别服务。 代码结构如下: 模板页面代码文件如下: upload.html : <!DOCTYPE html> <html> <meta charset"utf-8"> …...

9.8 校招 实习 内推 面经
绿泡*泡: neituijunsir 交流裙 ,内推/实习/校招汇总表格 1、校招 | 长安福特2024校园招聘正式启动 校招 | 长安福特2024校园招聘正式启动 2、2023校招总结--SLAM岗位 - 5 2023校招总结--SLAM岗位 - 5 3、校招&实习 | 格灵深瞳2024秋季校园招聘启…...

web前段与后端的区别优漫动游
要了解web前后端的区别,首先必须得清楚什么是web前端和web后端。 web前段与后端的区别 首先:web的本意是蜘蛛网和网的意思,在网页设计中我们称为网页的意思。现广泛译作网络、互联网等技术领域。表现为三种形式,即超文本(hyp…...
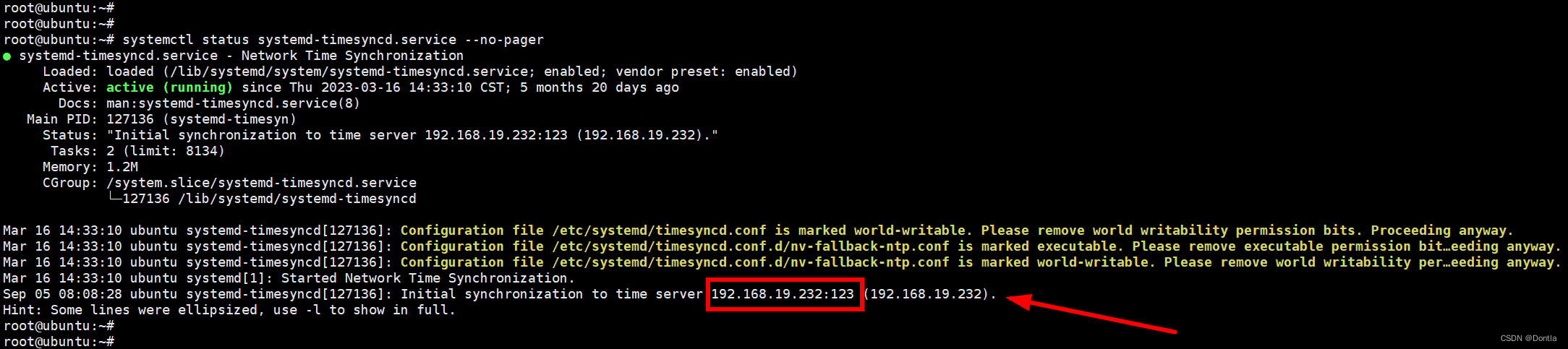
局域网ntp服务器设置(windows时间同步服务器NetTime)(ubuntu systemd-timesyncd ntp客户端)123端口、ntp校时
文章目录 背景windows如何配置ntp服务器手动配置配置参数AnnounceFlags和Enabled含义 使用软件配置(NetTime)实操相关疑问:0.nettime.pool.ntp.org是什么? 注意事项请务必检查windows主机123端口是否已被占用,方法请参…...

【个人博客系统网站】我的博客列表页 · 增删改我的博文 · 退出登录 · 博客详情页 · 多线程应用
【JavaEE】进阶 个人博客系统(4) 文章目录 【JavaEE】进阶 个人博客系统(4)1. 增加博文1.1 预期效果1.1 约定前后端交互接口1.2 后端代码1.3 前端代码1.4 测试 2. 我的博客列表页2.1 期待效果2.2 显示用户信息以及博客信息2.2.1…...

安全狗陈奋:数据安全需要建立在传统网络安全基础之上
8月22日-23日,由创业邦主办的“2023 DEMO WORLD 企业开放式创新大会”在上海顺利举行。 作为国内云原生安全领导厂商,安全狗受邀出席此次活动。 本次大会以“拥抱开放”为主题,聚焦开放式创新,通过演讲分享、专场对接、需求发布…...
【Redis】深入探索 Redis 的数据类型 —— 哈希表 hash
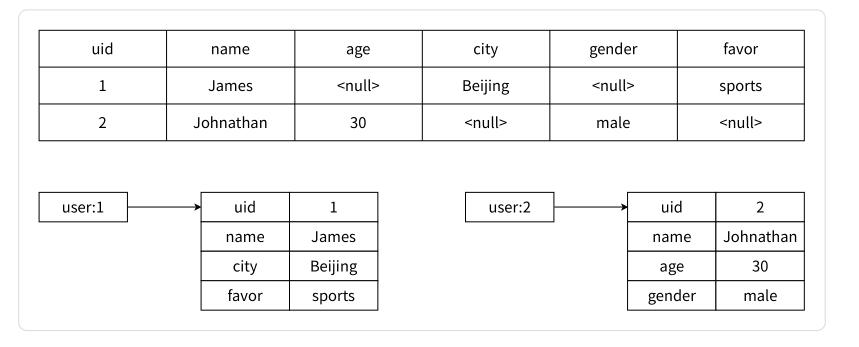
文章目录 前言一、hash 类型相关命令1.1 HSET 和 HSETNX1.2 HGET 和 HMGET1.3 HKEYS、HVALS 和 HGETALL1.4 HEXISTS 和 HDEL1.5 HLEN1.6 HINCRBY 和 HINCRBYFLOAT1.7 哈希相关命令总结 二、hash 类型内部编码三、hash 类型的应用场景四、原生,序列化,哈希…...
)
网络安全应急响应典型案例-(DDOS类、僵尸网络类、数据泄露类)
一、DDOS类事件典型案例 DDOS攻击,即分布式拒绝服务攻击,其目的在于使目标电脑的网络或系统资源耗尽,使服务暂时中断或停止,导致其正常用户无法访问。CC攻击使用代理服务器向受害服务器发送大量貌似合法的请求(通常…...

【测试开发】Mq消息重复如何测试?
本篇文章主要讲述重复消费的原因,以及如何去测试这个场景,最后也会告诉大家,目前互联网项目关于如何避免重复消费的解决方案。 Mq为什么会有重复消费的问题? Mq 常见的缺点之一就是消息重复消费问题,产生这种问题的原因是什么呢…...

C++和C#程序语言的区别
一直学习C++和C#,两者之间的区别总结一下 目录 一、两种语言概述 C++语言 C#语言 二、两种语言对比 2.1运行依赖...

CentOS配置Java环境报错-bash: /usr/local/jdk1.8.0_381/bin/java: 无法执行二进制文件
CentOS配置Java环境后执行java -version时报错: -bash: /usr/local/jdk1.8.0_381/bin/java: 无法执行二进制文件原因是所使用的jdk的版本和Linux内核架构匹配不上 使用以下命令查看Linux架构: [rootlocalhost ~]# cat /proc/version Linux version 3.1…...
MySQL进阶 —— 超详细操作演示!!!(上)
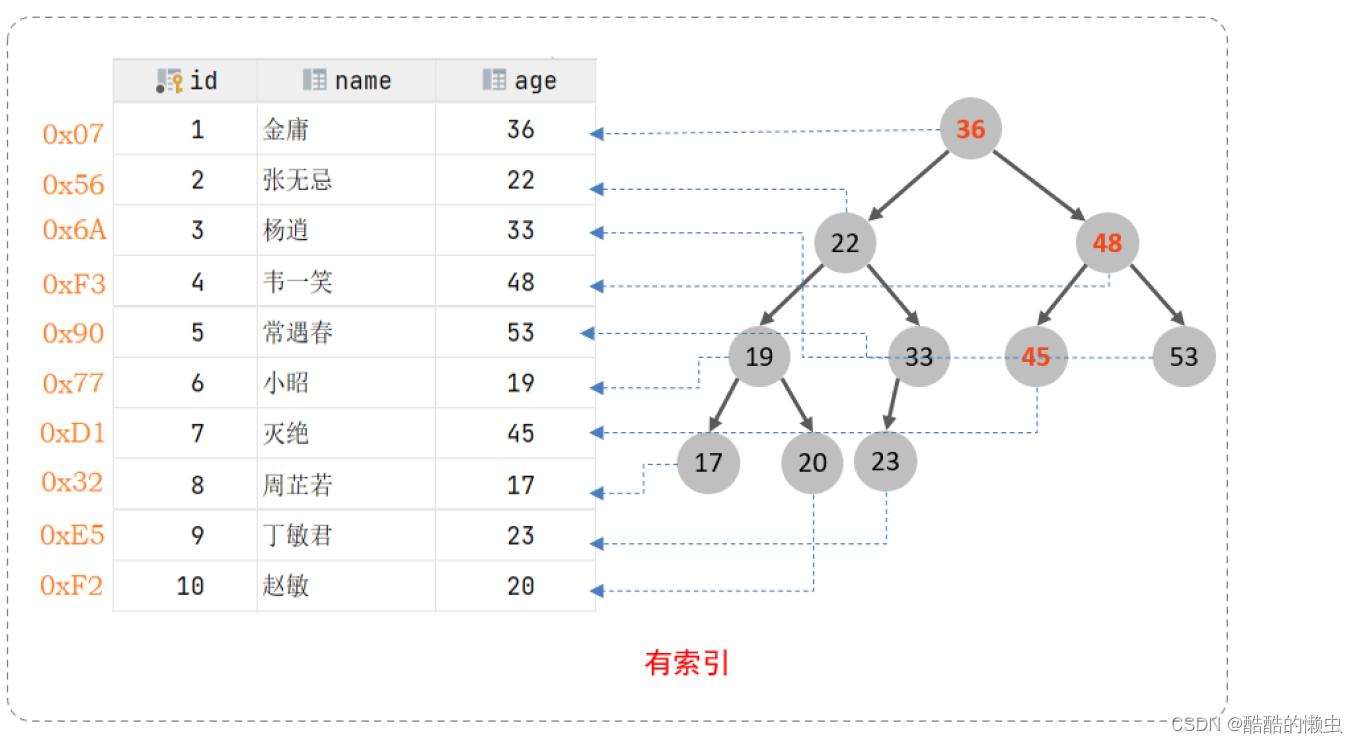
MySQL进阶 —— 超详细操作演示!!!(上) 一、存储引擎1.1 MySQL 体系结构1.2 存储引擎介绍1.3 存储引擎特点1.4 存储引擎选择 二、索引2.1 索引概述2.2 索引结构2.3 索引分类2.4 索引语法2.5 SQL 性能分析2.6 索引使用2…...
一条爬虫抓取一个小网站所有数据
一条爬虫抓取一个小网站所有数据 今天闲来无事,写一个爬虫来玩玩。在网上冲浪的时候发现了一个搞笑的段子网,发现里面的内容还是比较有意思的,于是心血来潮,就想着能不能写一个Python程序,抓取几条数据下来看看&am…...

八大排序——快速排序
Hello,大家好,今天分享的八大排序里的快速排序,所谓快速排序是一个叫霍尔的人发明,有很多人可能会觉得为什么不叫霍尔排序,其中原因就是因为它快,快速则体现了它的特点,今天我们就来讲一下快速排…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
