当前位置： 首页 > news >正文

k8s-实战——yapi平台部署

news 2026/2/9 1:12:20

文章目录

  • k8s 部署yapi平台
    • 前言
    • 准备工作
      • 构建yapi镜像
        • Dockerfile
        • entrypoint.sh
        • build.sh
        • 源码下载
        • 构建镜像
    • 启动mongo数据库
      • 新建nfs服务
      • mongo
        • 创建mongo服务
        • 初始化数据
      • 启动yapi服务
        • 创建yapi服务
        • 查看密码
      • 访问地址

k8s 部署yapi平台

前言

部署yapi平台需要mo

相关文章：

k8s-实战——yapi平台部署

文章目录 k8s 部署yapi平台前言准备工作构建yapi镜像Dockerfileentrypoint.shbuild.sh源码下载构建镜像启动mongo数据库新建nfs服务mongo创建mongo服务初始化数据启动yapi服务创建yapi服务查看密码访问地址k8s 部署yapi平台 前言 部署yapi平台需要mo...

编程日记 2023/9/10 2:02:21

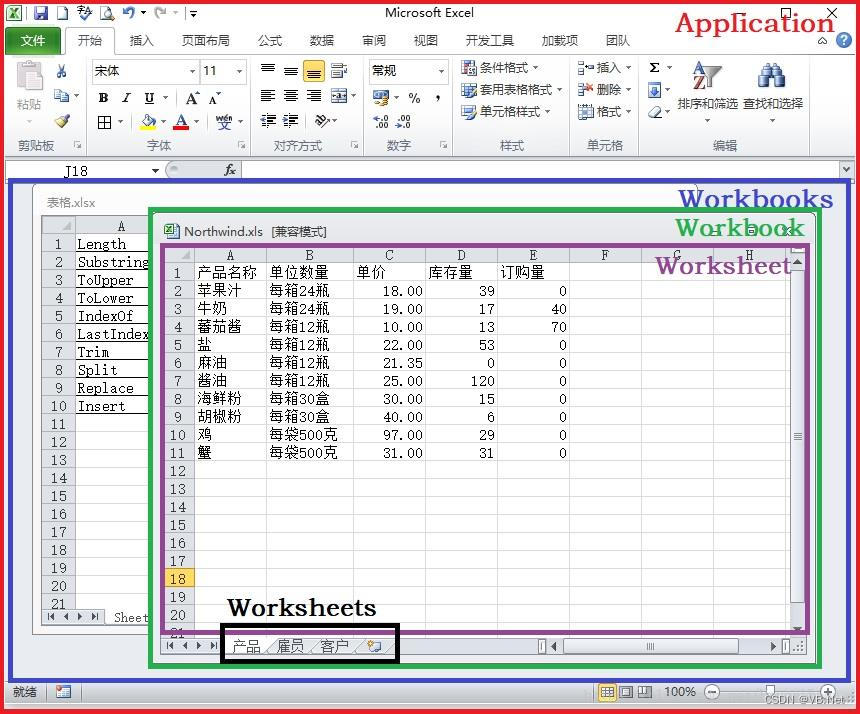
Excel VSTO开发5 -Excel对象结构

版权声明：本文为博主原创文章，转载请在显著位置标明本文出处以及作者网名，未经作者允许不得用于商业目的。 5 Excel对象结构 Excel提供了几个比较重要的对象： Application、Workbooks、Workbook、Worksheets、Worksheet 为了便…...

编程日记 2023/9/10 2:01:19

Javafx集成sqlite数据库

什么是SQLite SQLite是一款非常轻量级的关系数据库系统，支持多数SQL92标准。SQLite在使用前不需要安装设置，不需要进程来启动、停止或配置，而其他大多数SQL数据库引擎是作为一个单独的服务器进程，被程序使用某种内部进程通信(典型…...

编程日记 2023/9/10 2:00:17

react-native实现 TextInput 键盘显示搜索按钮并触发回调

<TextInput returnKeyType"search"returnKeyLabel"搜索"onSubmitEditing{e > {toSearch(keyword);}} /><SearchBarref{serachBarEl}placeholder"请输入"onChangeText{handleChangeSearch}value{search}onSubmitEditing{handleSearch…...

编程日记 2023/9/10 1:59:15

人大金仓分析型数据库备份和恢复（五）

增量备份 gpbackup和gprestore工具支持创建追加优化表的增量备份以及从增量备份还原。 只有表被更改时&#xff0c;增量备份才会备份所有指定的堆表和追加优化的表&#xff08;包括追加优化的&#xff0c;面向列的表&#xff09;。 例如&#xff0c;如果追加优化表的行已更改&a…...

编程日记 2023/9/10 1:58:09

lenovo联想笔记本ThinkPad P16V Gen 1(21FC,21FD)原装出厂Win11系统

原厂W11系统自带所有驱动、出厂主题壁纸、Office办公软件、联想电脑管家等预装程序 链接&#xff1a;https://pan.baidu.com/s/17dTExDSz-EDN4Qd-PZGJuw?pwdrgl3 提取码&#xff1a;rgl3 所需要工具&#xff1a;32G或以上的U盘 文件格式&#xff1a;ISO 文件大小…...

编程日记 2023/9/10 1:57:09

Django实现音乐网站 ⒃

使用Python Django框架制作一个音乐网站&#xff0c; 本篇主要是歌手详情页-专辑列表、专辑详情-单曲列表开发实现内容。 目录 歌手详情-专辑列表 路由设置 跳转设置 视图方法 模板内容 专辑详情-单曲列表 设置路由 视图处理并返回 模板渲染 分页优化 引入错误类型库…...

编程日记 2023/9/10 1:56:08

【开发问题系列】CSV转Excel

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...

编程日记 2023/9/10 1:55:05

mysql物理备份步骤

原库10.153.88.5&#xff0c;新建数据库实例10.153.88.6&#xff0c;注意/etc/my.cnf配置和88.5一致&#xff0c;测试目的是通过copy数据文件到88.6来恢复数据库。 在数据库10.153.88.5打包数据文件&#xff1a; [mysqlt3-dtpoc-dtpoc-web04 mysql]$ cd /testdata/mysql [mys…...

编程日记 2023/9/10 1:54:03

react使用hook封装一个tab组件

目录 react使用hook封装一个tab组件Tabbar.jsx使用组件效果 react使用hook封装一个tab组件 Tabbar.jsx import PropsTypes from "prop-types"; import React, { useEffect, useState } from react; export default function Tabbar(props) {const { tabData , cur…...

编程日记 2023/9/10 1:53:02

java详细安装教程（供参考）一一java（jdk）安装

一、java历史简介 1991 年Sun公司的James Gosling等人开始开发名称为 Oak &#xff08;橡树&#xff09;的语言。希望用于控制嵌入在有线电视交换盒、PDA等的微处理器&#xff0c; 1994年将Oak语言更名为Java 1998年JDK1.2时&#xff0c;更名为Java 2 Platform 分为标准版J…...

编程日记 2023/9/10 1:51:58

C++函数内联详解

本文旨在讲解C中的函数内联相关知识&#xff0c;读完这篇文章&#xff0c;希望读者们会对函数内联有更深一步的认识&#xff01; 内联函数的定义 在计算机科学中&#xff0c; 内联函数 &#xff08;有时称作 在线函数 或 编译时期展开函数 &#xff09;是一种编程语言结构&…...

编程日记 2023/9/10 1:50:57

Revit SDK 介绍：NewForm 新建体量

前言 这个例子介绍如何新建体量。 内容 图形生成效果。 用 Extrusion 创建体量 // 创建一个轮廓 ReferenceArray ref_ar new ReferenceArray(); // 创建三条直线&#xff0c;并放入轮廓 Autodesk.Revit.DB.XYZ ptA new Autodesk.Revit.DB.XYZ(10, 10, 0); Autodesk.Rev…...

编程日记 2023/9/10 1:49:56

Ubuntu离线或在线安装Python解释器

这里以安装Python3.5.7为例。 首先进入官网&#xff0c;下载Python-3.5.7.tgz&#xff0c;或者使用以下命令下载&#xff08;需要联网&#xff09;&#xff1a; wget https://www.python.org/ftp/python/3.5.7/Python-3.5.7.tgz下载完成后&#xff0c;使用以下命令进行解压缩…...

编程日记 2023/9/10 1:48:55

微信小程序隐私协议相关接口实际使用方式

<view wx:if"{{showPrivacy}}" class"privacy"><view class"popup"><view>隐私弹窗内容....</view><view bindtap"openPrivacyAgreement">点击查看隐私协议</view><button id"disagreeBt…...

编程日记 2023/9/10 1:47:55

MySQL--MySQL表的增删改查（进阶）

check 聚合查找 count sum average max min 我们这里先构造出多张表 查询lisi同学的成绩 来自student和来自score c 增加名字这一条件 查询所有同学的总成绩以及个人信息 来自score和来自student 查询所有同学的各科成绩以及个人信息 来自student&#xff0c;course和…...

编程日记 2023/9/10 1:46:53

Golang 中的静态类型和动态类型

定义说明 静态类型&#xff08;static type&#xff09;&#xff1a;在编码时就能确定的类型&#xff0c;通过变量定义可以确定的类型&#xff1b;动态类型&#xff08;concrete type&#xff09;&#xff1a;在运行时才能确定具体的数据类型&#xff1b; 动态静态类型如何理…...

编程日记 2023/9/10 1:45:50

docker的数据卷、docker数据持久化

目录 前言docker数据持久化的2种方式数据卷 bind mount &#xff0c;即-v参数匿名数据卷 docker manager volume-v参数和匿名卷的区别docker volume 命令的使用数据卷容器孤儿volume总结 前言 环境&#xff1a;centos7.9 docker version 20.10.14 本篇我们来介绍docker的数据卷…...

编程日记 2023/9/10 1:44:49

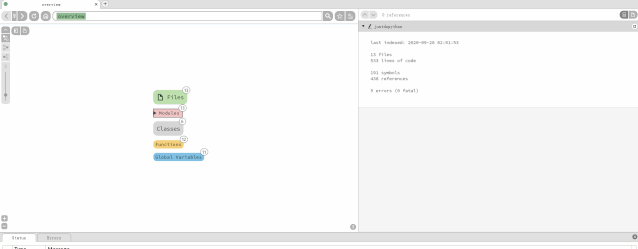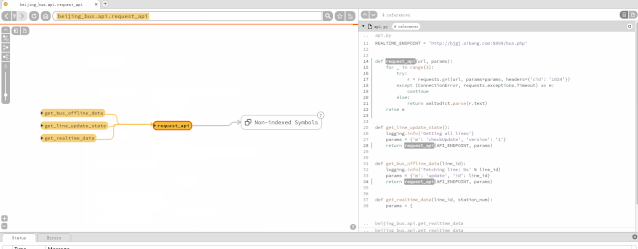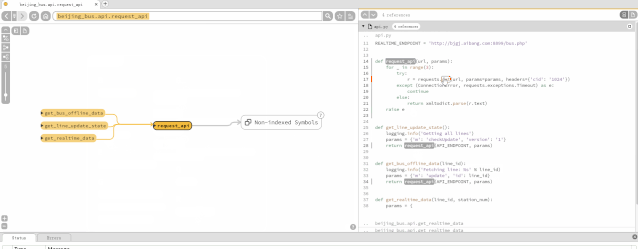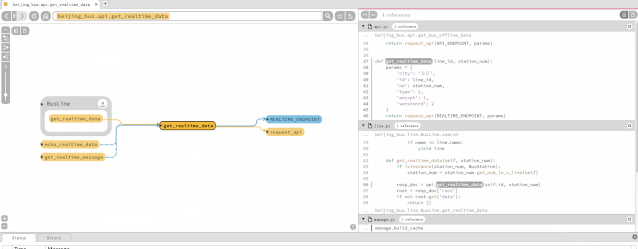
阅读源码工具Sourcetrail

收费工具Source Insight、Understand Sourcetrail开源工具 一、下载安装 接下来就是download&#xff0c;在GitHub的release页面选择自己系统对应的发布版本下载安装&#xff1a; 安装好后&#xff0c;运行程序&#xff0c;会出现这样的界面&#xff1a; 二、应用 选择“New…...

编程日记 2023/9/10 1:43:48

KMP 算法详解

KMP算法详解 1 KMP算法解决的问题 2 前缀问题 3 KMP 算法 1 KMP算法解决的问题 字符串str1和str2&#xff0c;str1是否包含str2&#xff0c;如果包含返回str2在str1中开始的位置。并做到时间复杂度为 O ( n ) O(n) O(n) 2 前缀问题 求一个字符串中每个字符前缀和后缀相…...

编程日记 2023/9/10 1:42:47

SkyWalking 10.2.0 SWCK 配置过程

SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外&#xff0c;K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案&#xff0c;全安装在K8S群集中。 具体可参…...

编程新知 2025/8/23 5:51:08

盘古信息PCB行业解决方案：以全域场景重构，激活智造新未来

一、破局&#xff1a;PCB行业的时代之问 在数字经济蓬勃发展的浪潮中&#xff0c;PCB&#xff08;印制电路板&#xff09;作为 “电子产品之母”&#xff0c;其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透&#xff0c;PCB行业面临着前所未有的挑战与机遇。产品迭代…...

编程新知 2026/2/7 17:29:24

Python实现prophet 理论及参数优化

文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候&#xff0c;写过一篇简单实现&#xff0c;后期随着对该模型的深入研究&#xff0c;本次记录涉及到prophet 的公式以及参数调优&#xff0c;从公式可以更直观…...

编程新知 2026/1/27 5:01:54

ESP32 I2S音频总线学习笔记（四）： INMP441采集音频并实时播放

简介 前面两期文章我们介绍了I2S的读取和写入&#xff0c;一个是通过INMP441麦克风模块采集音频&#xff0c;一个是通过PCM5102A模块播放音频&#xff0c;那如果我们将两者结合起来&#xff0c;将麦克风采集到的音频通过PCM5102A播放&#xff0c;是不是就可以做一个扩音器了呢…...

编程新知 2026/2/5 8:19:14

Map相关知识

数据结构 二叉树 二叉树&#xff0c;顾名思义&#xff0c;每个节点最多有两个“叉”&#xff0c;也就是两个子节点&#xff0c;分别是左子 节点和右子节点。不过&#xff0c;二叉树并不要求每个节点都有两个子节点&#xff0c;有的节点只 有左子节点&#xff0c;有的节点只有…...

编程新知 2026/2/4 16:21:14

使用Spring AI和MCP协议构建图片搜索服务

目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式&#xff08;本地调用&#xff09; SSE模式&#xff08;远程调用&#xff09; 4. 注册工具提…...

编程新知 2026/1/25 14:31:47

【Redis】笔记｜第8节｜大厂高并发缓存架构实战与优化

缓存架构 代码结构 代码详情 功能点&#xff1a; 多级缓存&#xff0c;先查本地缓存&#xff0c;再查Redis&#xff0c;最后才查数据库热点数据重建逻辑使用分布式锁&#xff0c;二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

编程新知 2026/1/26 3:45:28

mac 安装homebrew (nvm 及git)

mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用&#xff1a; 方法一&#xff1a;使用 Homebrew 安装 Git&#xff08;推荐&#xff09; 步骤如下&#xff1a;打开终端&#xff08;Terminal.app&#xff09; 1.安装 Homebrew…...

编程新知 2026/1/30 4:58:21

探索Selenium：自动化测试的神奇钥匙

目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

编程新知 2025/11/19 18:06:51

在 Spring Boot 中使用 JSP

jsp&#xff1f; 好多年没用了。重新整一下 还费了点时间&#xff0c;记录一下。 项目结构&#xff1a; pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

编程新知 2026/2/4 11:39:13