经管博士科研基础【19】齐次线性方程组
1. 线性方程组

 2. 非线性方程组
2. 非线性方程组
非线性方程,就是因变量与自变量之间的关系不是线性的关系,这类方程很多,例如平方关系、对数关系、指数关系、三角函数关系等等。求解此类方程往往很难得到精确解,经常需要求近似解问题。相应的求近似解的方法也逐渐得到大家的重视。
3. 线性、非线性与齐次、非齐次概念总结
对于一个表示为f(x)=C的方程,如果f(x) 是一个线性映射,则称为线性方程,反之则称为非线性方程。另外,如果C=0, 则称此方程齐次(齐次在函数和方程上的定义不同,齐次方程指方程内没有和x无关的项C,即任何项皆和x有关)。
这里f(x)=C定义是很一般性的,其可为任何数字、向量、函数等,而f(x) 可以指任意映射,例如有条件限制(给定初始值或边界值)的微分或积分运算。如果内含有对的微分运算,此方程即是一个微分方程。
4. 齐次线性方程组解的条件
常数项均为零的方程组称之为齐次线性方程组。
相关文章:

经管博士科研基础【19】齐次线性方程组
1. 线性方程组 2. 非线性方程组 非线性方程,就是因变量与自变量之间的关系不是线性的关系,这类方程很多,例如平方关系、对数关系、指数关系、三角函数关系等等。求解此类方程往往很难得到精确解,经常需要求近似解问题。相应的求近似解的方法也逐渐得到大家的重视。 3. 线…...
 CSRF verification failed. Request aborted.)
django报错解决 Forbidden (403) CSRF verification failed. Request aborted.
django报错解决 Forbidden (403) CSRF verification failed. Request aborted. 报错内容 Forbidden (403) CSRF verification failed. Request aborted.Help Reason given for failure:Origin checking failed - https://active-mantis-distinct.ngrok-free.app does not mat…...

k8s-实战——yapi平台部署
文章目录 k8s 部署yapi平台前言准备工作构建yapi镜像Dockerfileentrypoint.shbuild.sh源码下载构建镜像启动mongo数据库新建nfs服务mongo创建mongo服务初始化数据启动yapi服务创建yapi服务查看密码访问地址k8s 部署yapi平台 前言 部署yapi平台需要mo...
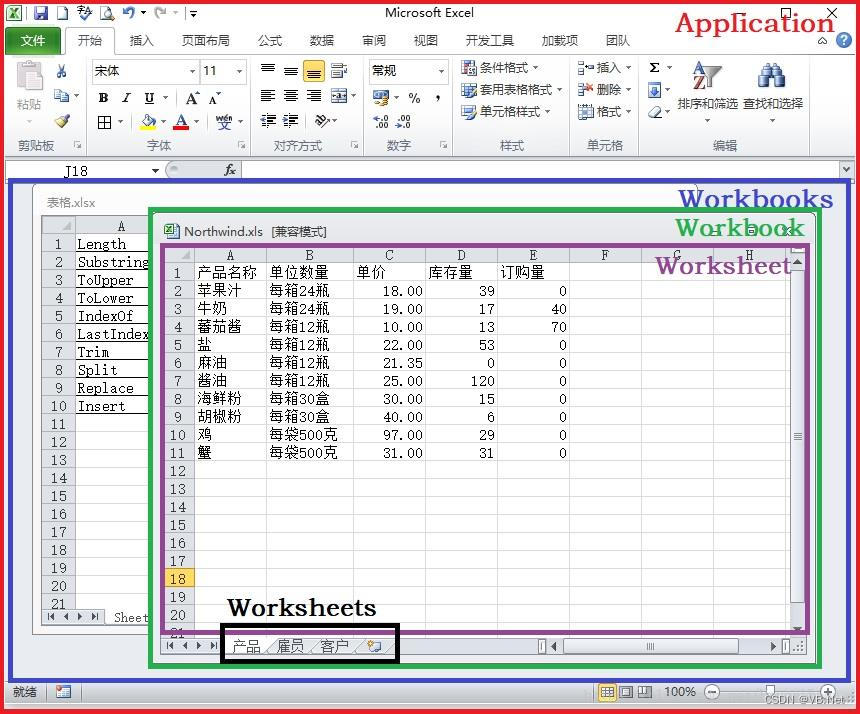
Excel VSTO开发5 -Excel对象结构
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 5 Excel对象结构 Excel提供了几个比较重要的对象: Application、Workbooks、Workbook、Worksheets、Worksheet 为了便…...

Javafx集成sqlite数据库
什么是SQLite SQLite是一款非常轻量级的关系数据库系统,支持多数SQL92标准。SQLite在使用前不需要安装设置,不需要进程来启动、停止或配置,而其他大多数SQL数据库引擎是作为一个单独的服务器进程,被程序使用某种内部进程通信(典型…...
react-native实现 TextInput 键盘显示搜索按钮并触发回调
<TextInput returnKeyType"search"returnKeyLabel"搜索"onSubmitEditing{e > {toSearch(keyword);}} /><SearchBarref{serachBarEl}placeholder"请输入"onChangeText{handleChangeSearch}value{search}onSubmitEditing{handleSearch…...
)
人大金仓分析型数据库备份和恢复(五)
增量备份 gpbackup和gprestore工具支持创建追加优化表的增量备份以及从增量备份还原。 只有表被更改时,增量备份才会备份所有指定的堆表和追加优化的表(包括追加优化的,面向列的表)。 例如,如果追加优化表的行已更改&a…...

lenovo联想笔记本ThinkPad P16V Gen 1(21FC,21FD)原装出厂Win11系统
原厂W11系统自带所有驱动、出厂主题壁纸、Office办公软件、联想电脑管家等预装程序 链接:https://pan.baidu.com/s/17dTExDSz-EDN4Qd-PZGJuw?pwdrgl3 提取码:rgl3 所需要工具:32G或以上的U盘 文件格式:ISO 文件大小…...

Django实现音乐网站 ⒃
使用Python Django框架制作一个音乐网站, 本篇主要是歌手详情页-专辑列表、专辑详情-单曲列表开发实现内容。 目录 歌手详情-专辑列表 路由设置 跳转设置 视图方法 模板内容 专辑详情-单曲列表 设置路由 视图处理并返回 模板渲染 分页优化 引入错误类型库…...

【开发问题系列】CSV转Excel
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...

mysql物理备份步骤
原库10.153.88.5,新建数据库实例10.153.88.6,注意/etc/my.cnf配置和88.5一致,测试目的是通过copy数据文件到88.6来恢复数据库。 在数据库10.153.88.5打包数据文件: [mysqlt3-dtpoc-dtpoc-web04 mysql]$ cd /testdata/mysql [mys…...

react使用hook封装一个tab组件
目录 react使用hook封装一个tab组件Tabbar.jsx使用组件效果 react使用hook封装一个tab组件 Tabbar.jsx import PropsTypes from "prop-types"; import React, { useEffect, useState } from react; export default function Tabbar(props) {const { tabData , cur…...
一一java(jdk)安装)
java详细安装教程(供参考)一一java(jdk)安装
一、java历史简介 1991 年Sun公司的James Gosling等人开始开发名称为 Oak (橡树)的语言。希望用于控制嵌入在有线电视交换盒、PDA等的微处理器, 1994年将Oak语言更名为Java 1998年JDK1.2时,更名为Java 2 Platform 分为标准版J…...

C++函数内联详解
本文旨在讲解C中的函数内联相关知识,读完这篇文章,希望读者们会对函数内联有更深一步的认识! 内联函数的定义 在计算机科学中, 内联函数 (有时称作 在线函数 或 编译时期展开函数 )是一种编程语言结构&…...

Revit SDK 介绍:NewForm 新建体量
前言 这个例子介绍如何新建体量。 内容 图形生成效果。 用 Extrusion 创建体量 // 创建一个轮廓 ReferenceArray ref_ar new ReferenceArray(); // 创建三条直线,并放入轮廓 Autodesk.Revit.DB.XYZ ptA new Autodesk.Revit.DB.XYZ(10, 10, 0); Autodesk.Rev…...

Ubuntu离线或在线安装Python解释器
这里以安装Python3.5.7为例。 首先进入官网,下载Python-3.5.7.tgz,或者使用以下命令下载(需要联网): wget https://www.python.org/ftp/python/3.5.7/Python-3.5.7.tgz下载完成后,使用以下命令进行解压缩…...

微信小程序隐私协议相关接口实际使用方式
<view wx:if"{{showPrivacy}}" class"privacy"><view class"popup"><view>隐私弹窗内容....</view><view bindtap"openPrivacyAgreement">点击查看隐私协议</view><button id"disagreeBt…...

MySQL--MySQL表的增删改查(进阶)
check 聚合查找 count sum average max min 我们这里先构造出多张表 查询lisi同学的成绩 来自student和来自score c 增加名字这一条件 查询所有同学的总成绩以及个人信息 来自score和来自student 查询所有同学的各科成绩以及个人信息 来自student,course和…...

Golang 中的静态类型和动态类型
定义说明 静态类型(static type):在编码时就能确定的类型,通过变量定义可以确定的类型;动态类型(concrete type):在运行时才能确定具体的数据类型; 动态静态类型如何理…...

docker的数据卷、docker数据持久化
目录 前言docker数据持久化的2种方式数据卷 bind mount ,即-v参数匿名数据卷 docker manager volume-v参数和匿名卷的区别docker volume 命令的使用数据卷容器孤儿volume总结 前言 环境:centos7.9 docker version 20.10.14 本篇我们来介绍docker的数据卷…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
