【面试经典150 | 数组】合并两个有序数组
文章目录
- 写在前面
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:合并排序
- 方法二:双指针
- 方法三:原地操作-从前往后
- 方法四:原地操作-从后往前
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【双指针】【原地操作-从前往后】【原地操作-从后往前】【排序】【数组】
题目来源
面试经典 150 题——88. 合并两个有序数组

题目解读
给定两个有序数组 nums1 和 nums2,现在需要合并两个数组到 nums1 中,nums1 中已经预留了合并的位置。
解题思路
方法一:合并排序
将数组nums2 合并到 nums1 数组中的空位上,再利用 sort() 函数进行排序。
时间复杂度: O ( ( m + n ) l o g ( m + n ) ) O((m+n)log(m+n)) O((m+n)log(m+n)),快速排序的时间复杂度。
空间复杂度: O ( l o g ( m + n ) ) O(log(m+n)) O(log(m+n)),快速排序占用的空间。
方法二:双指针
维护一个临时数组,用来存放合并后的数组。
使用两个指针 i,j,分别指向两数组首元素,迭代比较 i、j 位置处元素大小,将小的元素依次存入临时数组。
最后,将临时数组中元素移植到 nums1 数组中。
时间复杂度 O ( m + n ) O(m+n) O(m+n)。
空间复杂度 O ( m + n ) O(m+n) O(m+n),因为需要一个临时数组,大小为 m + n m+n m+n。
方法三:原地操作-从前往后
首先,重新定义一下双指针 i 和 j 的含义,两指针分别表示指向数组 nums1 和 nums2 当前没有使用过的最小的元素,i 也表示当前最小元素将要放置的位置。
在方法二中,我们之所以使用了一个临时数组来存放较小的数字,是因为我们从前往后枚举比较两指针指向的元素得到较小值,如果直接合并到 nums1 数组中,可能会覆盖掉 nums1 中接下来将要比较的数字(这也是原地操作删除有序数组中的重复元素的思想,具体内容可见 图解【原地操作】删除有序数组中的重复元素)。
直接合并有问题,那么我们进行交换处理保留较大数,即交换 nums1[i] 和 nums2[j],交换了之后,我们将较小的数放置在数组 nums1 的 i 位置处,较大的数放置在数组 nums2 的 j 位置处。这时候还需要对数组 nums2 进行排序,每次交换数字之后都要进行排序操作。
因为我们的双指针都是指向当前数组中最小的数字,交换操作有可能破坏数组 nums2 的升序结构。
下面以图示形式进行演示:
(1)双指针从 0 位置开始;

(2)nums1[0] < nums2[0],右移 i 指针;
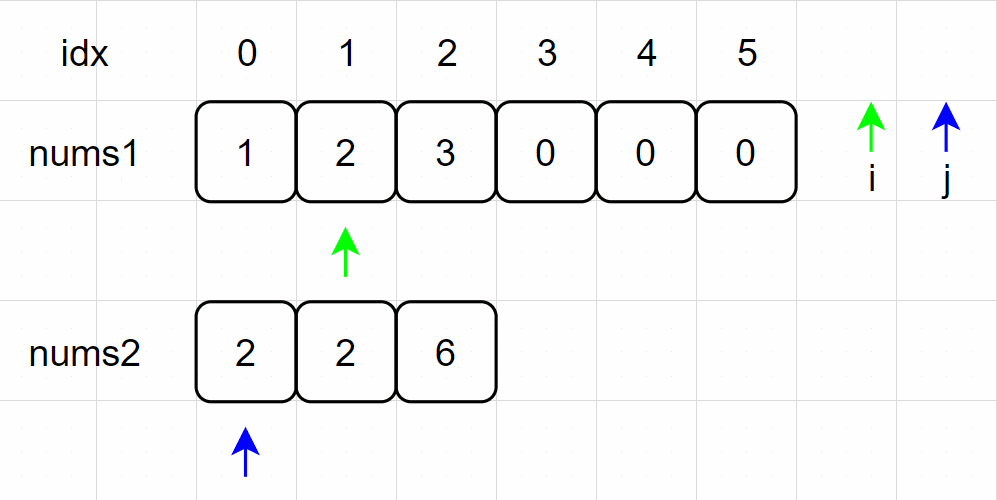
(3)nums1[1] = nums2[0],右移 i 指针;

(4)nums2[0] < nums1[2],交换数组中两元素;
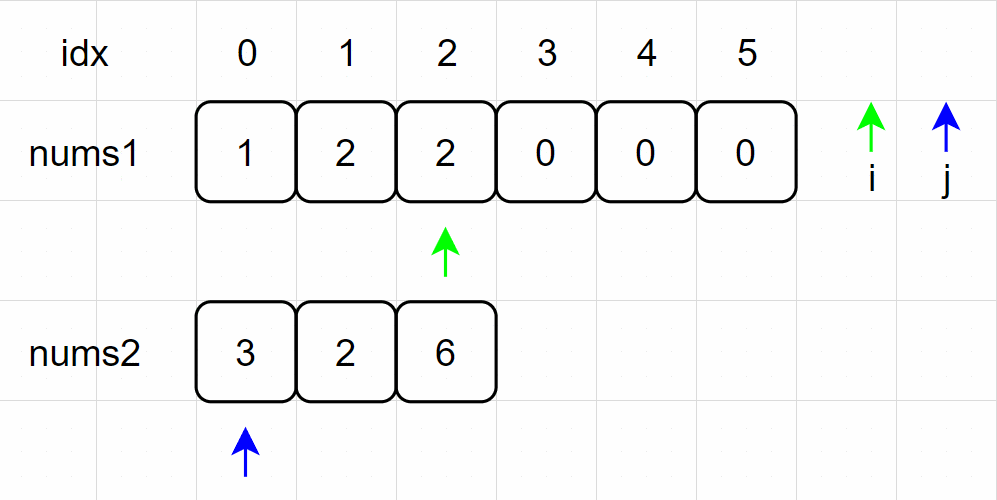
(5)nums2 数组的升序结构被破坏,需要进行升序排序;

(6)nums1[2] = nums2[0],右移 i 指针;
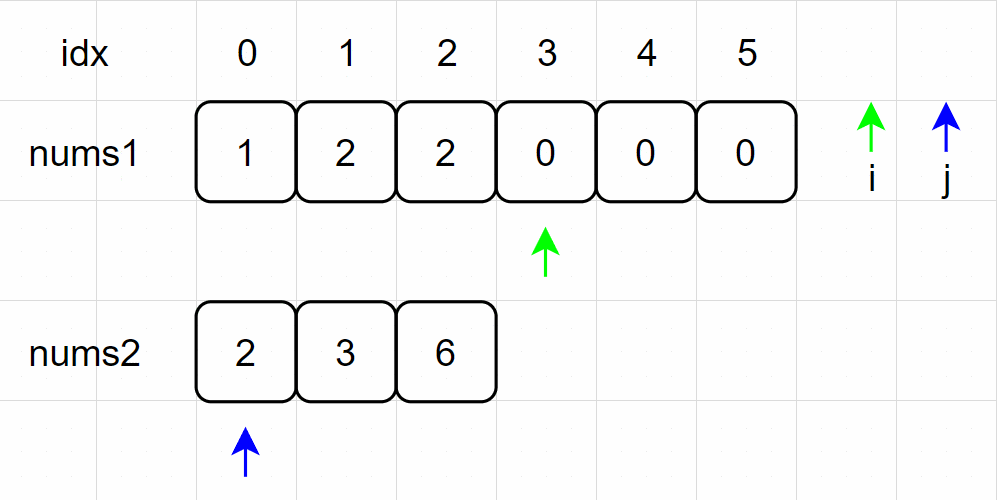
(7)数组 nums1 中前半部分数位已经填充完毕,后半部分占位符使用数组 nums2 填充,当前位置填充完毕之后,同时右移两指针;如此迭代填充,直至 j 指针越界,合并两个有序数组完成!

实现代码
class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {int i = 0, j = 0;while (j < n) {if (i >= m) {nums1[i] = nums2[j++];}else {if (nums1[i] > nums2[j]) {swap(nums1[i], nums2[j]);}sort(nums2.begin(), nums2.end());}++i;}}
};
时间复杂度: O ( m a x ( m , n l o g n ) ) O(max(m, nlogn)) O(max(m,nlogn))。
空间复杂度: O ( n l o g n ) O(nlogn) O(nlogn),快速排序占用的空间。
方法四:原地操作-从后往前
现在考虑从后往前处理,具体地维护三个指针,i 指向数组 nums1 比较元素的末尾即 m-n-1 位置,j 指针指向数组 nums2 比较元素的末尾即 n-1 位置,k 指针指向数组 nums1 的末尾即 m-1 位置。
我们比较 nums1[i] 和 nums2[j] 元素大小,将较大的元素放置在数组 nums1 的 k 位置处。
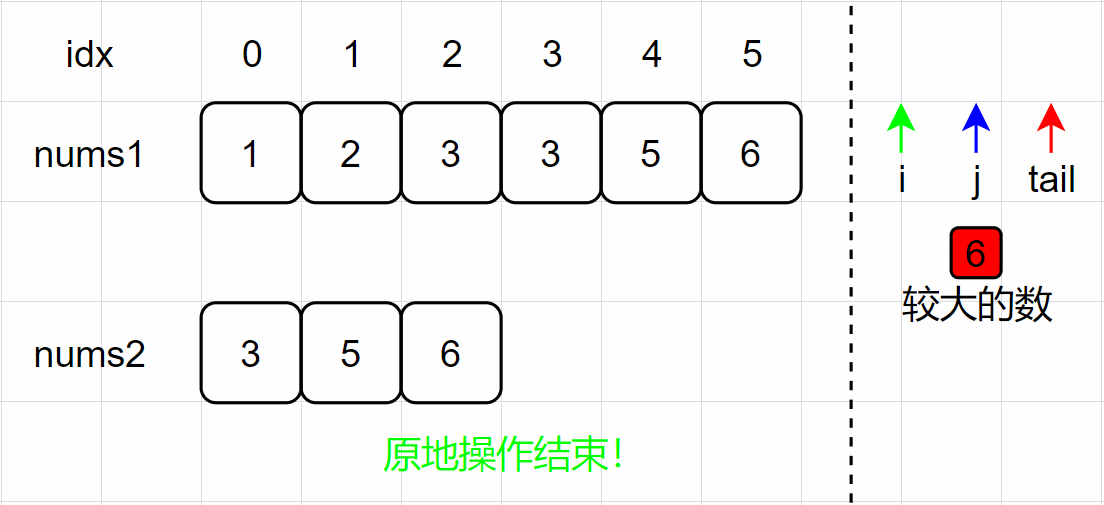
下面以图示形式进行演示:
(1)三指针初始化;

(2)nums1[2] < nums2[2] ,将较大的 nums2[2] 放置在 tail 处;
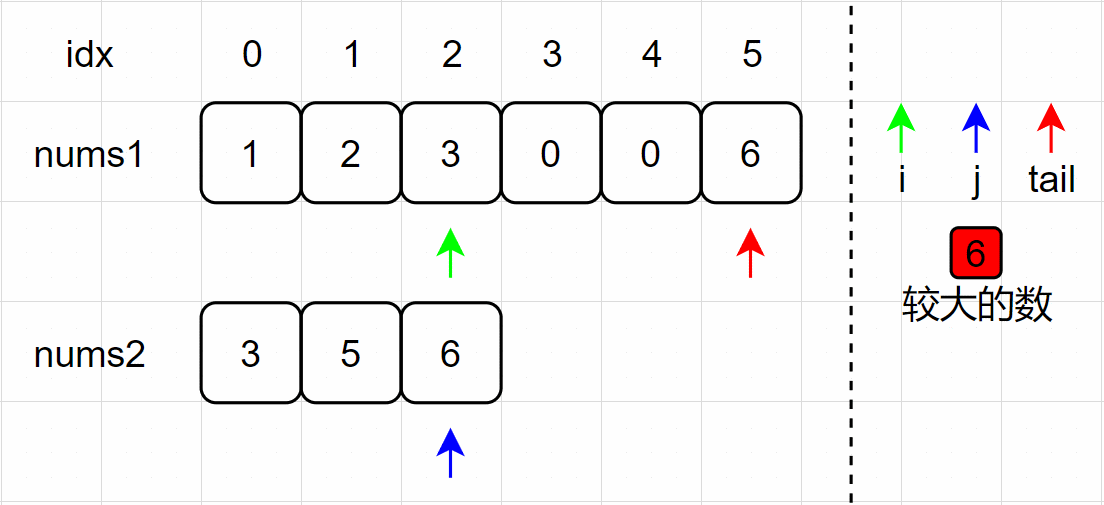
(3)j、tail 指针分别左移一个单位,为下次比较做准备;

(4) nums1[2] < nums2[1] ,将较大的 nums2[1] 放置在 tail 处;

(5)j、tail 指针分别左移一个单位,为下次比较做准备;
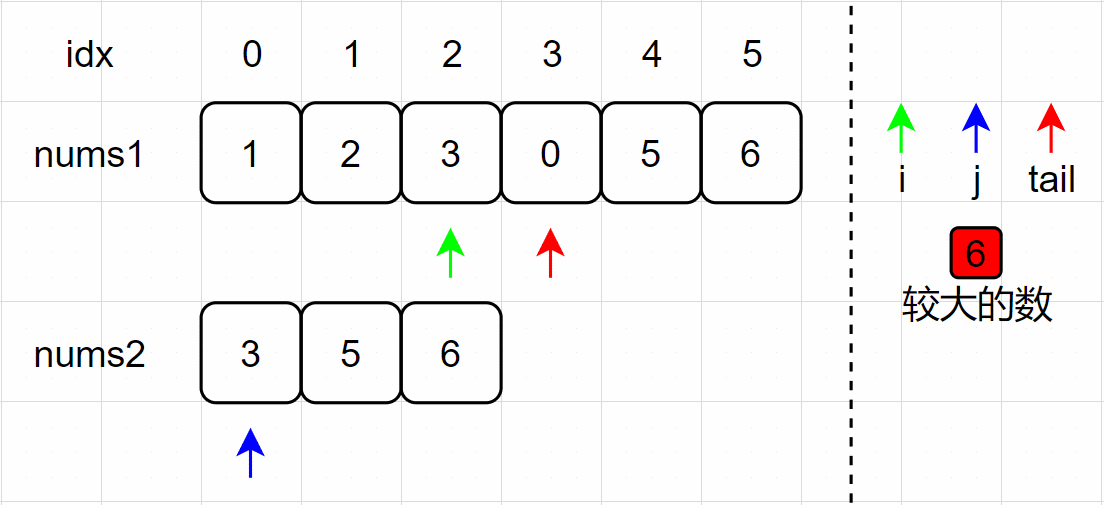
(6)nums1[2] = nums2[0] ,将 nums1[1] 放置在 tail 处;
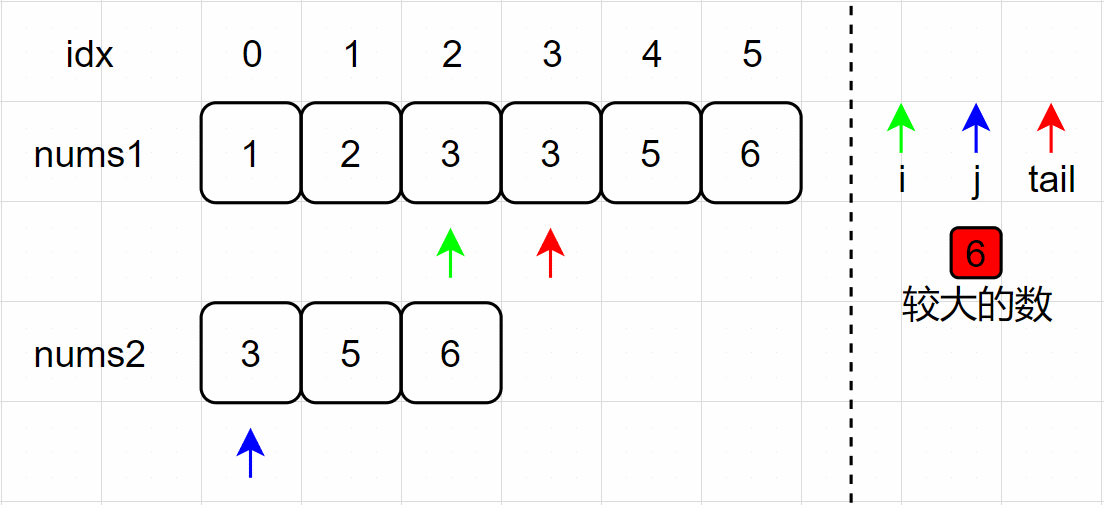
(7)i、tail 指针分别左移一个单位,为下次比较做准备;
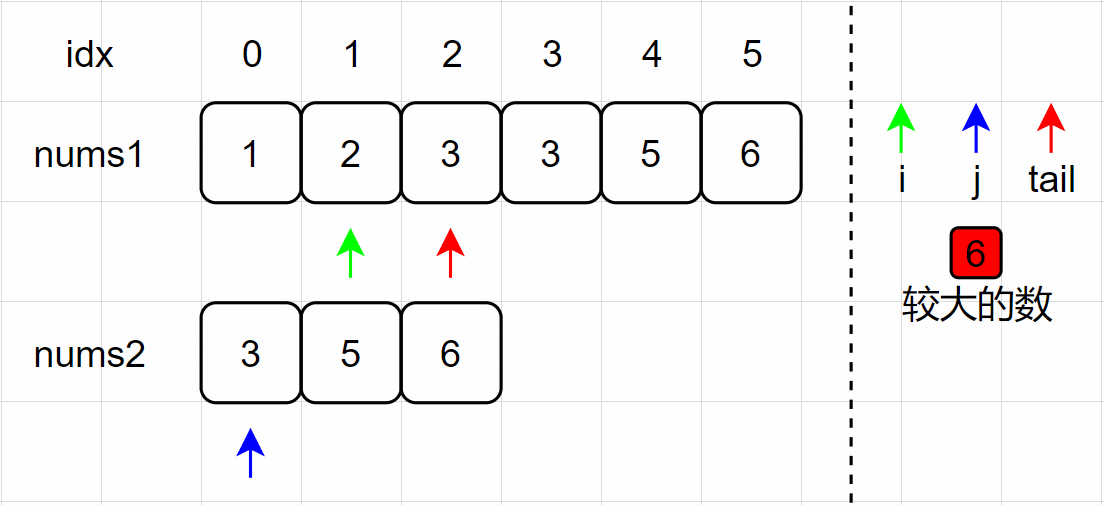
(8)nums1[1] < nums2[0] ,将较大的 nums2[0] 放置在 tail 处;
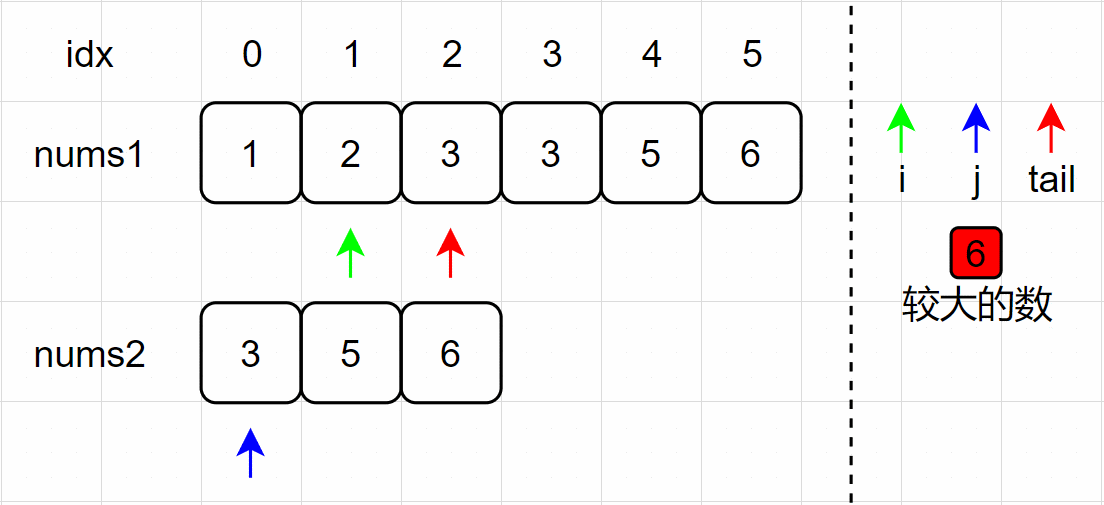
(9)j、tail 指针分别左移一个单位,j 指针越界,原地操作结束,数组 nums1 为最后合并后的数组。
实现代码
class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {int i = m - 1, j = n - 1, k = m + n - 1;while (i >= 0 && j >= 0) {if (nums2[j] > nums1[i]) {nums1[k--] = nums2[j--];}else {nums1[k--] = nums1[i--];}}while (j >= 0) {nums1[k--] = nums2[j--];}}
};
时间复杂度: O ( m + n ) O(m+n) O(m+n)。
空间复杂度: O ( 1 ) O(1) O(1),原地操作,仅仅使用了三个指针变量。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【面试经典150 | 数组】合并两个有序数组
文章目录 写在前面Tag题目来源题目解读解题思路方法一:合并排序方法二:双指针方法三:原地操作-从前往后方法四:原地操作-从后往前 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章…...

系统架构设计专业技能 ·操作系统
现在的一切都是为将来的梦想编织翅膀,让梦想在现实中展翅高飞。 Now everything is for the future of dream weaving wings, let the dream fly in reality. 点击进入系列文章目录 系统架构设计高级技能 操作系统 一、操作系统概述二、进程管理2.1 进程概念2.2 进…...

CSP 202209-1 如此编码
答题 题目就是字多 #include<iostream>using namespace std;int main() {int n,m;cin>>n>>m;int a[n],c[n1];c[0]1;for(int i0;i<n;i){cin>>a[i];c[i1]c[i]*a[i];}for(int i0;i<n;i){cout<<(m%c[i1]-m%c[i])/c[i]<< ;} }...
windows安装向量数据库milvus
本文介绍windows下安装milvus的方法。 一.Docker安装 1.1docker下载 首先到Docker官网上下载docker:Docker中文网 官网 1.2.安装前前期准备 先使用管理员权限打开windows powershell 然后在powershell里面输入下面那命令,启用“适用于 Linux 的 Windows 子系统”…...

Qt中,QScript对JavaScript的内置接口支持情况
支持 JSON.parse()/stringify() Object.keys() 不支持 console.info()/debug()/warn()/error() window setTimeout() clearTimeout() setInterval() clearInterval() 后续添加更多接口支持情况~...

C语言基础-typedef的用法
文章目录 前言基础用法高阶用法typedef作用于数组typedef作用于函数指针 总结 前言 熟悉C语言的同学,应该都见过typedef,但可能对typedef的用法并不是真的了解。本文介绍几种typedef的用法,相信会有所帮助 基础用法 一般typedef用来声明一个…...
Linux中安装MySQL5.7.42
1. 首先,下载mysql5.7.42的安装包(下方是下载地址),选择红色框框的下载(注意的是,这个链接只提供5.7的版本下载,可能还会更新,不一定打开就是5.7.42的版本,后续可能会有4…...

网络基础--1.网络纵横
网络的发展历程 计算机由原来的只能单一处理信息(单用户批处理)逐步发展为多用户批处理,可以实现一台计算机连接多个终端同时使用一台计算机(分时系统),但是多个终端之间不能相互通信,再发展成为…...

Django TypeError: Abstract models cannot be instantiated.错误解决方案
问题 [2023-09-05 10:23:41][dvadmin.utils.exception.CustomExceptionHandler():64] [ERROR] Traceback (most recent call last): File “D:\InstallSpace\Anaconda3\envs\py39\lib\site-packages\rest_framework\views.py”, line 506, in dispatch response handler(requ…...
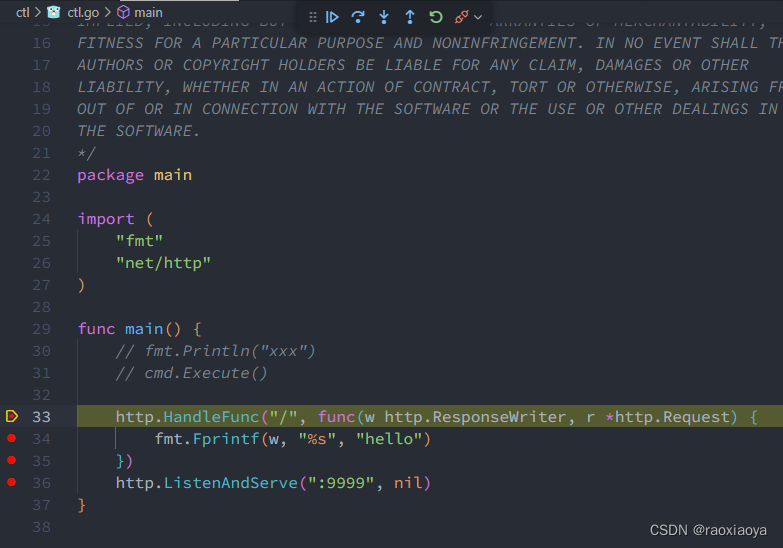
vscode使用delve调试golang程序
环境配置 delve仓库,含有教程:https://github.com/go-delve/delve golang的debugging教程:https://github.com/golang/vscode-go/wiki/debugging > go version go version go1.20 windows/amd64> go install github.com/go-delve/de…...
如何从任何苹果、Windows或安卓设备访问iCloud照片
本文介绍了如何在各种设备上访问iCloud照片库,包括iPhone和iPad、Mac、Windows PC和Android设备。说明适用于iOS 13及以上版本、iPadOS 13及以上、macOS Big Sur(10.16)和Catalina(10.15)、Windows 10或11以及Android 10。 从iPhone、iPod Touch和iPad访问iCloud照片 照…...
关于“找不到mfc140u.dll,无法继续执行代码”问题的分析处理方法
我想和大家分享一个在编程过程中经常会遇到的问题——找不到mfc140u.dll,无法继续执行代码。找不到 mfc140u.dll,这个问题可能会让我们感到困扰。mfc140u.dll 是 Microsoft Foundation Classes(MFC)库的一部分,它是一个 Windows 系…...

用 TripletLoss 优化bert ranking
下面是 用 TripletLoss 优化bert ranking 的demo import torch from torch.utils.data import DataLoader, Dataset from transformers import BertModel, BertTokenizer from sklearn.metrics.pairwise import pairwise_distancesclass TripletRankingDataset(Dataset):def __…...

Tomcat安装及使用
这里写目录标题 Tomcat一.java基础1.java历史2.java组成3.实现动态网页功能serveltjsp 4.jdkJDK 和 JRE 关系安装openjdk安装oracle官方JDK 二.tomcat基础功能1.Tomcat介绍2.安装tomcat二进制安装Tomcat 3.配置文件介绍及核心组件配置文件组件 4.状态页5.常见的配置详解6.tomca…...

法国新法案强迫 Firefox 等浏览器审查网站
导读Mozilla 基金会已发起了一份请愿书,旨在阻止法国政府强迫 Mozilla Firefox 等浏览器审查网站。 据悉,法国政府正在制定一项旨在打击网络欺诈的 SREN 法案 (“Projet de loi Visant scuriser et reguler lespace numrique”),包含大约 2…...

开源电商项目 Mall:构建高效电商系统的终极选择
文章目录 Mall 项目概览前台商城系统后台管理系统系统架构图业务架构图 模块介绍后台管理系统 mall-admin商品管理:功能结构图-商品订单管理:功能结构图-订单促销管理:功能结构图-促销内容管理:功能结构图-内容用户管理࿱…...
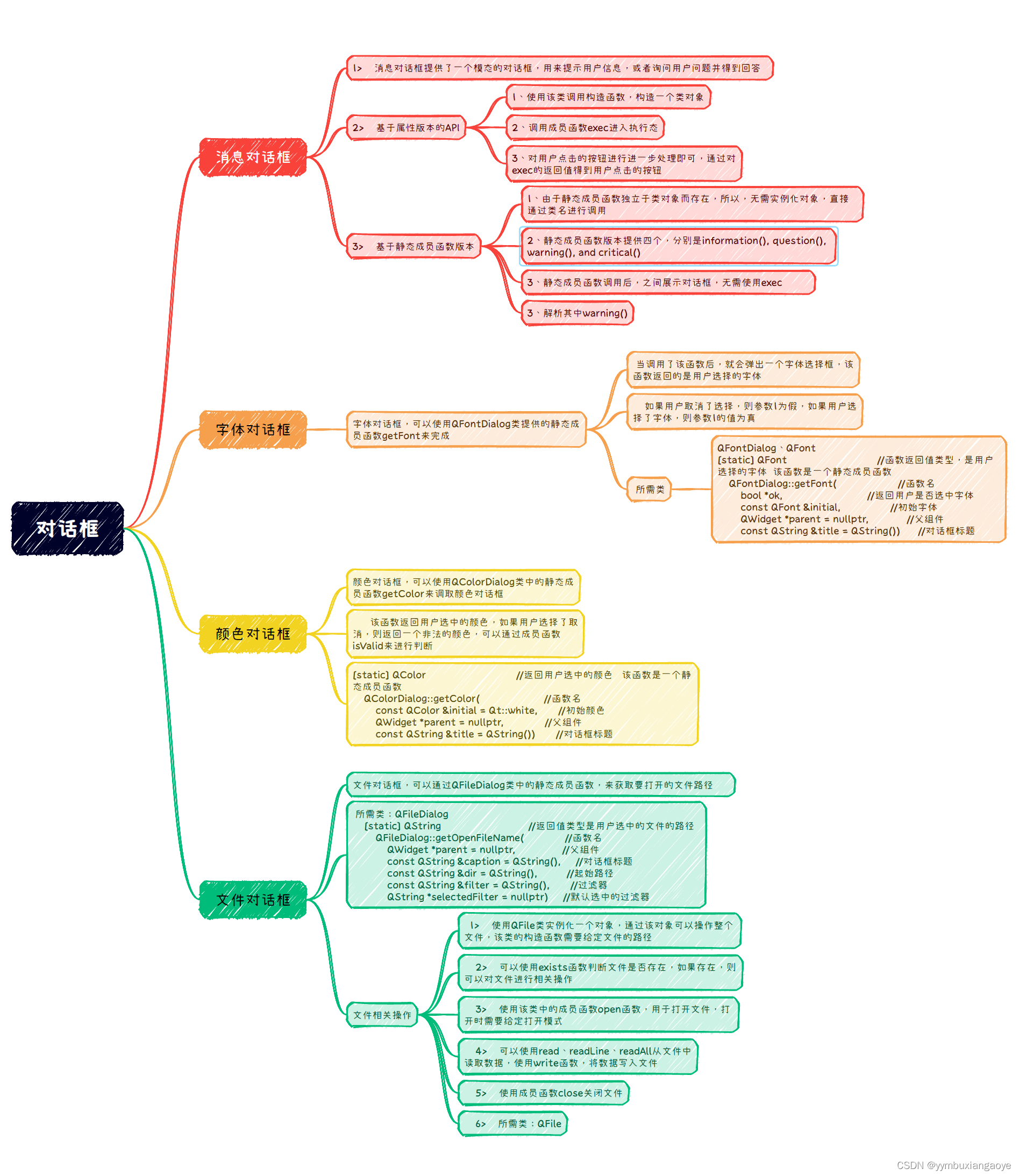
QT(9.1)对话框与事件处理
作业: 1. 完善登录框 点击登录按钮后,判断账号(admin)和密码(123456)是否一致,如果匹配失败,则弹出错误对话框,文本内容“账号密码不匹配,是否重新登录”&…...
C++项目实战——基于多设计模式下的同步异步日志系统-③-前置知识补充-设计模式
文章目录 专栏导读六大原则单例模式饿汉模式懒汉模式 工厂模式简单工厂模式工厂方法模式抽象工厂模式 建造者模式代理模式 专栏导读 🌸作者简介:花想云 ,在读本科生一枚,C/C领域新星创作者,新星计划导师,阿…...

C++ 新旧版本两种读写锁
一、简介 读写锁(Read-Write Lock)是一种并发控制机制,用于多线程环境中实现对共享资源的高效读写操作。读写锁允许多个线程同时读取共享资源,但在有写操作时,需要互斥地独占对共享资源的访问,以确保数据的…...
方法)
ES6 字符串的repeat()方法
repeat() 方法返回一个新字符串,表示将原字符串重复n次 格式:str.repeat(n) 参数n:str需要重复多少次 参数n的取值: n是正整数: x.repeat(3) // 输出结果:"xxx" hello.repeat(2) // 输出结果…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
