ES6 字符串的repeat()方法
repeat() 方法返回一个新字符串,表示将原字符串重复n次
格式:
str.repeat(n)
参数n:str需要重复多少次
参数n的取值:
-
n是正整数:
'x'.repeat(3) // 输出结果:"xxx" 'hello'.repeat(2) // 输出结果:"hellohello" -
n是负整数或Infinity,会报错
'na'.repeat(Infinity) // RangeError 'na'.repeat(-1) // RangeError -
n是0
'na'.repeat(0) // 输出结果:"" -
n是小数,会向下取整
'na'.repeat(2.9) // 输出结果:"nana" -
n是0到-1之间的小数,则等同于 0,因为会先进行取整运算,0 到-1 之间的小数取整后等于-0,repeat视同为 0
'na'.repeat(-0.9) // 输出结果:"" -
n是NaN / null / undefined,就等同于 0
'na'.repeat(NaN) // 输出结果:"" 'na'.repeat(null) // 输出结果:"" 'na'.repeat(undefined) // 输出结果:"" -
n是字符串,则会先转换成数字
'na'.repeat('na') // 输出结果:"" 'na'.repeat('3') // 输出结果:"nanana"
相关文章:
方法)
ES6 字符串的repeat()方法
repeat() 方法返回一个新字符串,表示将原字符串重复n次 格式:str.repeat(n) 参数n:str需要重复多少次 参数n的取值: n是正整数: x.repeat(3) // 输出结果:"xxx" hello.repeat(2) // 输出结果…...

【车载以太网测试从入门到精通】系列文章目录汇总
【车载以太网测试从入门到精通】——物理层测试 【车载以太网测试从入门到精通】——数据链路层测试 【车载以太网测试从入门到精通】——网络层测试 【车载以太网测试从入门到精通】——传输层测试 【车载以太网测试从入门到精通】——以太网TCP/IP协议自动化测试(…...
LLM推理优化技术综述:KVCache、PageAttention、FlashAttention、MQA、GQA
LLM推理优化技术综述:KVCache、PageAttention、FlashAttention、MQA、GQA 随着大模型被越来越多的应用到不同的领域,随之而来的问题是应用过程中的推理优化问题,针对LLM推理性能优化有一些新的方向,最近一直在学习和研究…...
go开发之个微机器人的二次开发
请求URL: http://域名/addRoomMemberFriend 请求方式: POST 请求头Headers: Content-Type:application/jsonAuthorization:login接口返回 参数: 参数名必选类型说明wId是String登录实例标识chatRoom…...

2023国赛数学建模B题思路代码 - 多波束测线问题
# 1 赛题 B 题 多波束测线问题 单波束测深是利用声波在水中的传播特性来测量水体深度的技术。声波在均匀介质中作匀 速直线传播, 在不同界面上产生反射, 利用这一原理,从测量船换能器垂直向海底发射声波信 号,并记录从声波发射到…...
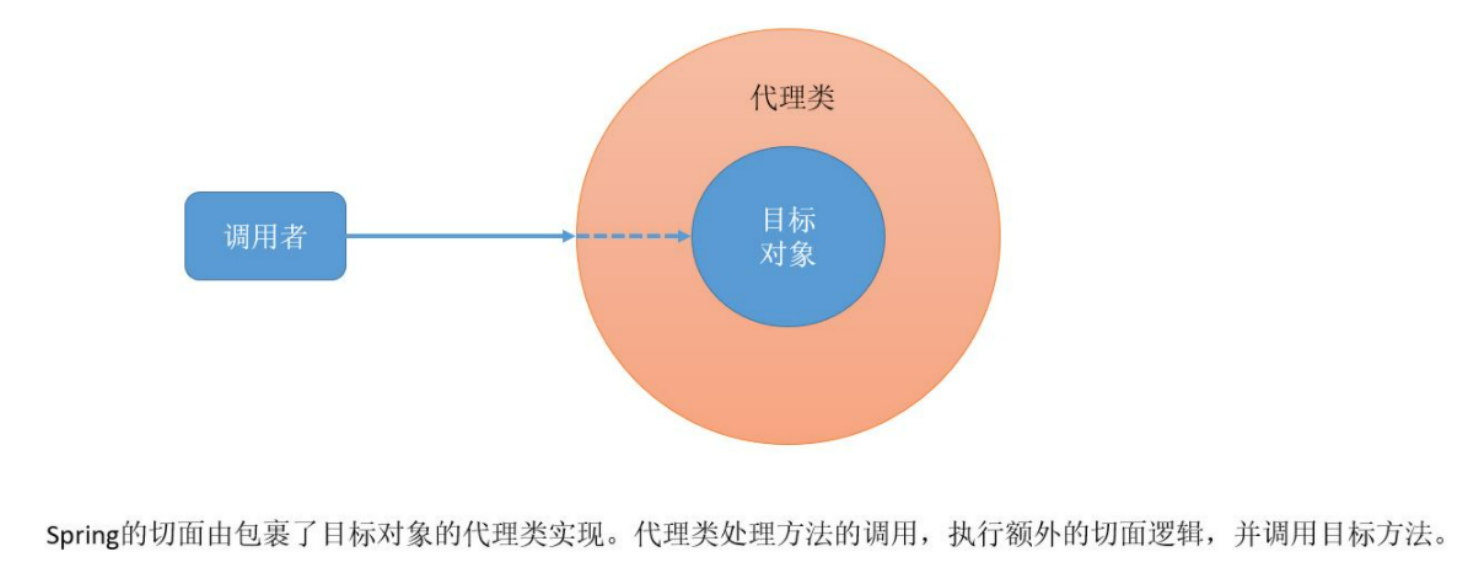
SpringAOP面向切面编程
文章目录 一. AOP是什么?二. AOP相关概念三. SpringAOP的简单演示四. SpringAOP实现原理 一. AOP是什么? AOP(Aspect Oriented Programming):面向切面编程,它是一种编程思想,是对某一类事情的集…...

A Guide to Java HashMap
原文链接: A Guide to Java HashMap → https://www.baeldung.com/java-hashmap 从Map里取值 # 原生方法 Map<String, Integer> map new HashMap<>();// map自身的方法 → 取不到返回null Integer age6 map.get("name"); // Integer时返回null可…...

LeetCode 449. Serialize and Deserialize BST【树,BFS,DFS,栈】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
:IAR中ICF链接文件详解和实例分析)
嵌入式IDE(1):IAR中ICF链接文件详解和实例分析
最近在使用NXP的提供的MCUXPresso IDE,除了Eclipse固有的优点外,我觉得它最大的优点就是在链接脚本的生成上,提供了非常直观的GUI配置界面。但这个IDE仅仅支持NXP相关的产品,而且调试的性能在某些情况下并不理想。而我们用得比较多…...
分布式版本控制工具——git
✅<1>主页::我的代码爱吃辣 📃<2>知识讲解:Linux——git ☂️<3>开发环境:Centos7 💬<4>前言:git是一个开源的分布式版本控制系统,可以有效、高速地处理从很…...
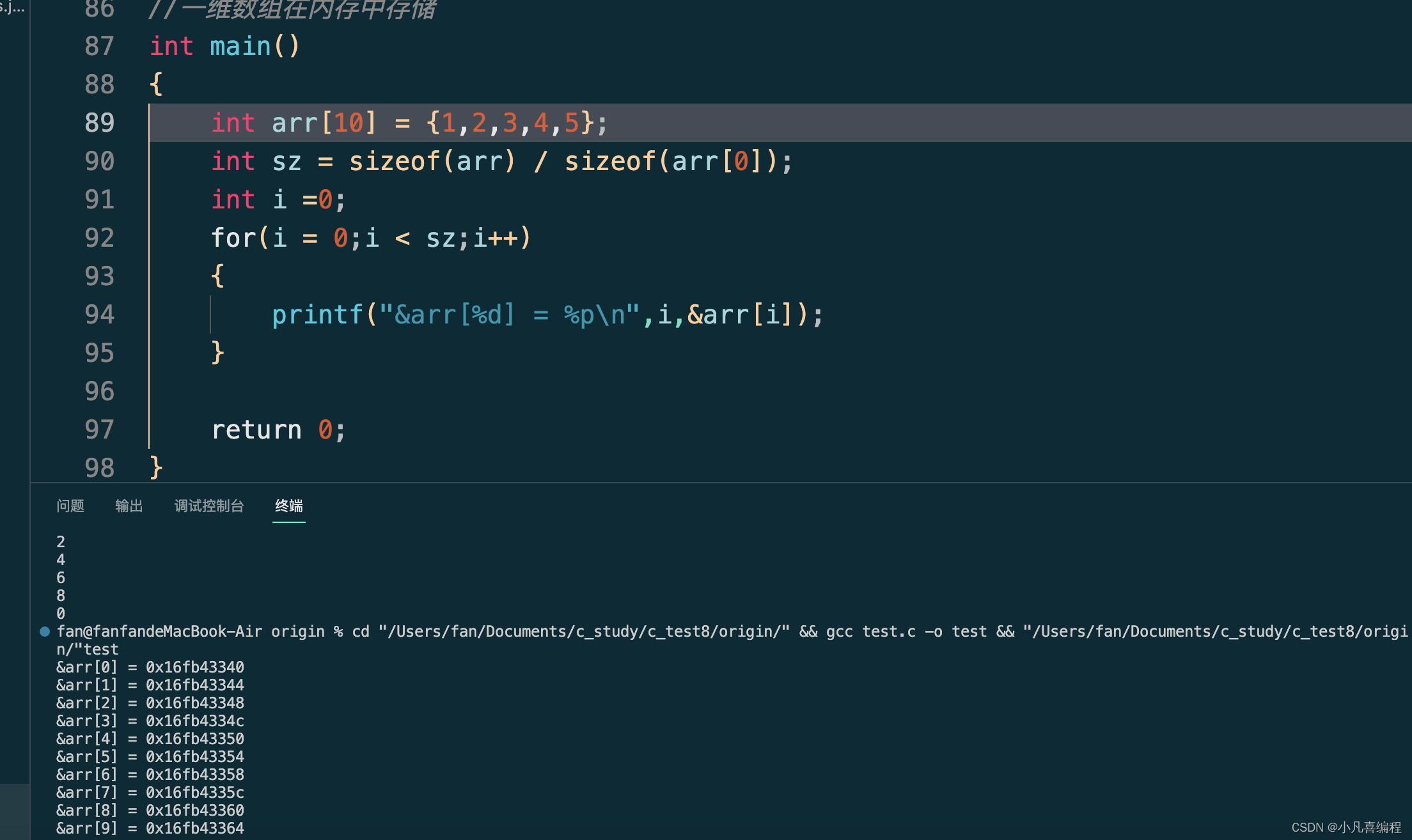
C基础-数组
1.一维数组的创建和初始化 int main() {// int arr1[10];int n 0;scanf("%d",&n);//int count 10;int arr2[n]; //局部的变量,这些局部的变量或者数组是存放在栈区的,存放在栈区上的数组,如果不初始化的话,默认…...

springboot项目配置flyway菜鸟级别教程
1、Flyway的工作原理 Flyway在第一次执行时,会创建一个默认名为flyway_schema_history的历史记录表,这张表会用来跟踪或记录数据库的状态,然后每次项目启动时都会自动扫描在resources/db/migration下的文件的版本号并且通过查询flyway_schem…...

成都精灵云初试
最近参加了成都精灵云的笔试与面试,岗位是c工程师。后面自己复盘了过程,初试部分总结如下,希望能对各位相进该公司以及面试C工程师的同学提供一些参考。这也是博主第一次参加面试,很多东西都还没准备,很多答得不好&…...

css relative 和absolute布局
1、relative和absolute内部的元素都是相对于父容器,若父容器没有指定为relative,则默认为整个文档视图空间,absolute可以重叠元素,relative则不行。relative意味着元素的任意属性如left和right都是相对于其他元素的。absolute则相…...

更健康舒适更科技的照明体验!书客SKY护眼台灯SUKER L1上手体验
低价又好用的护眼台灯是多数人的需求,很多人只追求功能性护眼台灯,显色高、无频闪、无蓝光等基础需求。但是在较低价格中很难面面俱到,然而刚发布的SUKER书客L1护眼台灯却是一款不可多得的性价比护眼台灯,拥有高品质光源ÿ…...

经管博士科研基础【19】齐次线性方程组
1. 线性方程组 2. 非线性方程组 非线性方程,就是因变量与自变量之间的关系不是线性的关系,这类方程很多,例如平方关系、对数关系、指数关系、三角函数关系等等。求解此类方程往往很难得到精确解,经常需要求近似解问题。相应的求近似解的方法也逐渐得到大家的重视。 3. 线…...
 CSRF verification failed. Request aborted.)
django报错解决 Forbidden (403) CSRF verification failed. Request aborted.
django报错解决 Forbidden (403) CSRF verification failed. Request aborted. 报错内容 Forbidden (403) CSRF verification failed. Request aborted.Help Reason given for failure:Origin checking failed - https://active-mantis-distinct.ngrok-free.app does not mat…...

k8s-实战——yapi平台部署
文章目录 k8s 部署yapi平台前言准备工作构建yapi镜像Dockerfileentrypoint.shbuild.sh源码下载构建镜像启动mongo数据库新建nfs服务mongo创建mongo服务初始化数据启动yapi服务创建yapi服务查看密码访问地址k8s 部署yapi平台 前言 部署yapi平台需要mo...
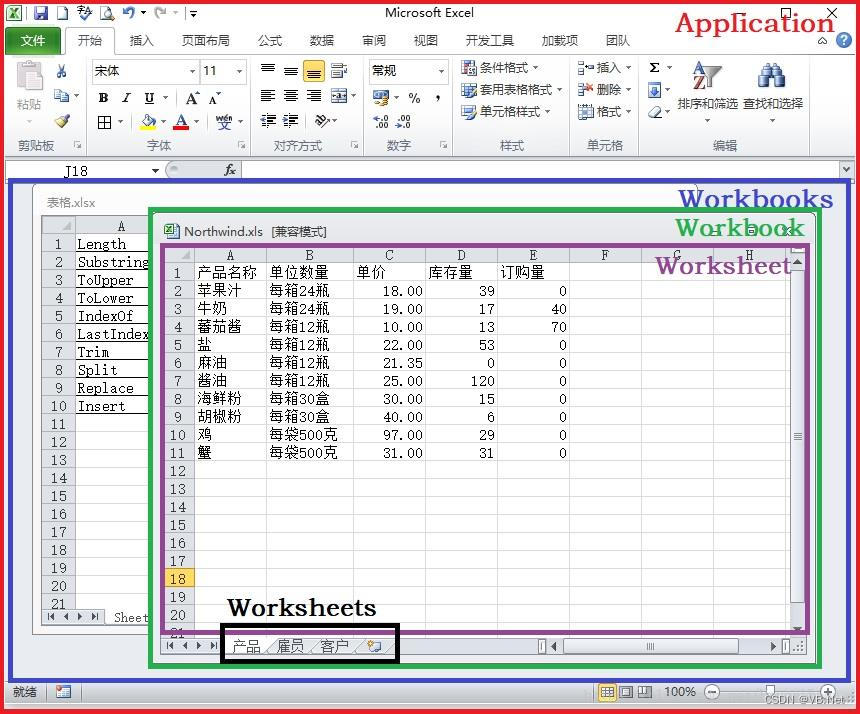
Excel VSTO开发5 -Excel对象结构
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 5 Excel对象结构 Excel提供了几个比较重要的对象: Application、Workbooks、Workbook、Worksheets、Worksheet 为了便…...

Javafx集成sqlite数据库
什么是SQLite SQLite是一款非常轻量级的关系数据库系统,支持多数SQL92标准。SQLite在使用前不需要安装设置,不需要进程来启动、停止或配置,而其他大多数SQL数据库引擎是作为一个单独的服务器进程,被程序使用某种内部进程通信(典型…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...
