LeetCode刷题笔记【23】:贪心算法专题-1(分发饼干、摆动序列、最大子序和)
文章目录
- 前置知识
- 贪心算法的本质
- 什么时候用贪心算法?
- 什么时候不能用贪心?
- 贪心算法的解题步骤
- 455.分发饼干
- 题目描述
- 解题思路
- 代码
- 376. 摆动序列
- 题目描述
- 解题思路
- 代码
- 53. 最大子序和
- 题目描述
- 暴力解法
- 动态规划
- 贪心算法
- 总结
前置知识
贪心算法的本质
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
例如,有一堆钞票,你可以拿走十张,如果想达到最大的金额,你要怎么拿?
指定每次拿最大的,最终结果就是拿走最大数额的钱。
每次拿最大的就是局部最优,最后拿走最大数额的钱就是推出全局最优。
什么时候用贪心算法?
- 感觉像是可以用贪心
- 用题中的案例试一下, 发现没问题
- 尝试举一下反例, 发现没问题
- 那就可以用了
所以贪心算法并没有固定的规律和套路, 也不会要求你论证背后算法的合理性和有效性, 只要能解决问题, 通过测试案例即可.
ps:个人认为贪心非常虚无缥缈呀, 还是动态规划更加有迹可循;
并且在实践过程中, 可以用贪心算法的, 基本都可以用动态规划.
什么时候不能用贪心?
当局部最优, 不一定可以达到全局最优的时候, 如:
有一堆盒子,你有一个背包体积为n,如何把背包尽可能装;
如果还每次选最大的盒子,就不行了。
这时候就需要动态规划。
贪心算法的解题步骤
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
这样的叙述非常抽象, 实践过程中还是要把握思想: 选择每一阶段的局部最优,从而达到全局最优
参考文章:关于贪心算法, 你该了解这些
455.分发饼干
题目描述
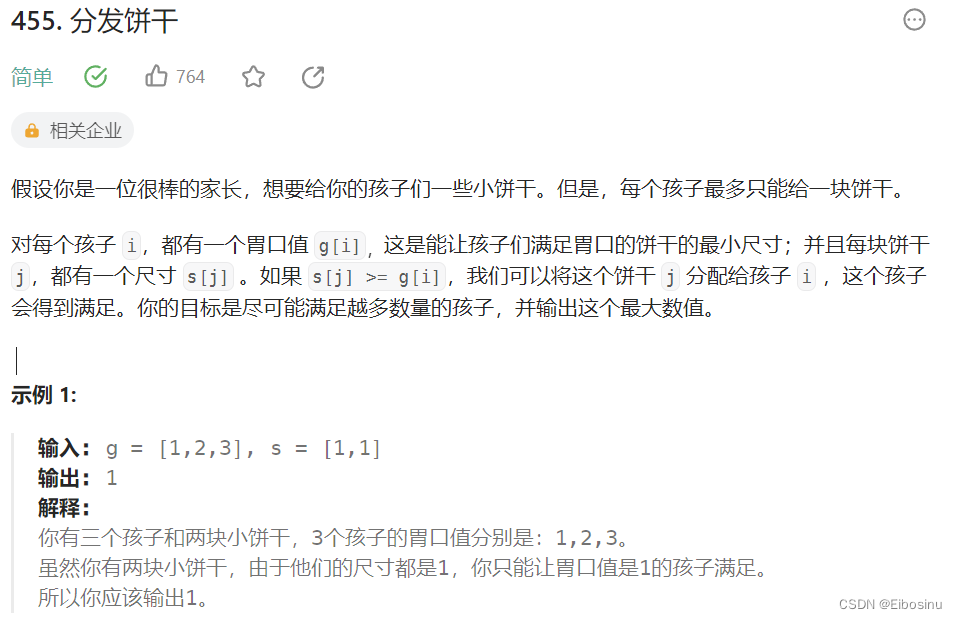
LeetCode链接:https://leetcode.cn/problems/assign-cookies/description/
解题思路
思路: 先将两个数组都srot
遍历g数组, 优先满足胃口最小的孩子
遍历g数组中的元素gg的时候, 依次遍历s数组, 选择能满足gg的最小尺寸饼干
代码
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {int ans=0;sort(g.begin(), g.end());sort(s.begin(), s.end());int ss=0;for(int gg : g){for(; ss<s.size(); ++ss){if(s[ss] >= gg){s[ss] = 0;ans++;break;}}}return ans;}
};
376. 摆动序列
题目描述

LeetCode链接:https://leetcode.cn/problems/wiggle-subsequence/description/
解题思路
<代>: 其实过程中不需要对数组进行操作, 只需要看有多少个点是符合要求的即可;
具体过程比较复杂, 建议参考其原文.
代码
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n=nums.size();if(n==0 || n==1 || (n==2 && nums[0]!=nums[1]))return n;int curDiff = 0;int preDiff = 0;int ans=1;for(int i=0; i<n-1; ++i){curDiff = nums[i+1] - nums[i];if((preDiff<=0 && curDiff>0) || (preDiff>=0 && curDiff<0)){ans++;preDiff = curDiff;}}return ans;}
};
53. 最大子序和
题目描述

LeetCode链接:https://leetcode.cn/problems/maximum-subarray/description/
暴力解法
思路: 暴力解法
对数组中每个数, 都依次向后遍历所有子数组, 求和, 和ans取max
class Solution {
public:int maxSubArray(vector<int>& nums) {int ans=INT_MIN;for(int i=0; i<nums.size(); ++i){int sum=0;for(int j=i; j<nums.size(); ++j){sum += nums[j];ans = max(ans, sum);}}return ans;}
};动态规划
不出所料的, 超出时间限制;
用动态规划, 创建数组maxSum
nums[0]的maxSum[0]就是自己本身
之后的nums[i]的maxSum[i]=max(nums[i], maxSum[i-1]+nums[i])
class Solution {
public:int maxSubArray(vector<int>& nums) {if(nums.size()==1)return nums[0];vector<int> maxSum(nums.size());maxSum[0] = nums[0];int ans=nums[0];for(int i=1; i<nums.size(); ++i){maxSum[i] = max(nums[i], maxSum[i-1]+nums[i]);ans = max(ans, maxSum[i]);}return ans;}
};
优化: 不用数组用pre
class Solution {
public:int maxSubArray(vector<int>& nums) {int ans = nums[0];int pre = nums[0];for(int i=1; i<nums.size(); ++i){pre = max(pre+nums[i], nums[i]);ans = max(ans, pre);}return ans;}
};
贪心算法

选取一个个"区间", 过程中用count记录区间内的和;
当count<0时, 将其清空(=0)
class Solution {
public:int maxSubArray(vector<int>& nums) {int ans = INT_MIN;int count=0;for(int i=0; i<nums.size(); ++i){count += nums[i];ans = max(ans, count);if(count<0)count = 0;}return ans;}
};
总结
相比于动态规划, 贪心算法的思路难把握的多, 也很难以揣摩;
所以过程中如果想不出来, 第一反应应该是尝试动态规划, 或者直接看题解;
一方面不要在做题过程中硬磕贪心算法;
另一方面在学习的时候, 不要过于较真, 对于贪心这一部分的内容, 可以适当抱着"了解"和:"探索学习"的心态.
把精力多花在可以比较快比较好地掌握和把握的部分和方法上.
本文参考:
分发饼干
摆动序列
最大子序和
相关文章:

LeetCode刷题笔记【23】:贪心算法专题-1(分发饼干、摆动序列、最大子序和)
文章目录 前置知识贪心算法的本质什么时候用贪心算法?什么时候不能用贪心?贪心算法的解题步骤 455.分发饼干题目描述解题思路代码 376. 摆动序列题目描述解题思路代码 53. 最大子序和题目描述暴力解法动态规划贪心算法 总结 前置知识 贪心算法的本质 贪心的本质是选择每一阶…...
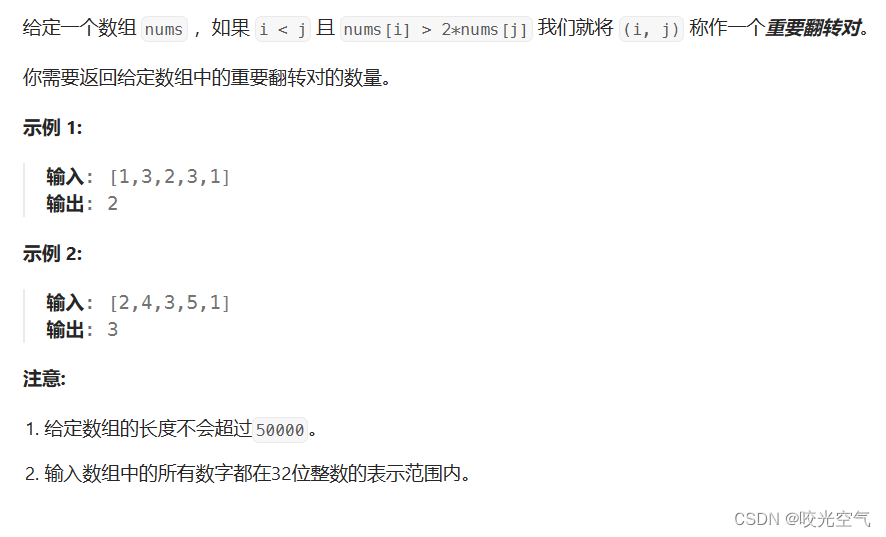
C++算法 —— 分治(2)归并
文章目录 1、排序数组2、数组中的逆序对3、计算右侧小于当前元素的个数4、翻转对 本篇前提条件是已学会归并排序 1、排序数组 912. 排序数组 排序数组也可以用归并排序来做。 vector<int> tmp;//写成全局是因为如果在每一次小的排序中都创建一次,更消耗时间和…...

Hadoop YARN HA 集群安装部署详细图文教程
目录 一、YARN 集群角色、部署规划 1.1 集群角色--概述 1.2 集群角色--ResourceManager(RM) 1.3 集群角色--NodeManager(NM) 1.4 HA 集群部署规划 二、YARN RM 重启机制 2.1 概述 2.2 演示 2.2.1 不开启 RM 重启机制…...

BBS+商城项目的数据库表设计
本文章是对于BBS商城项目的数据库的初步设计,仅供参考! -- 创建用户表 CREATE TABLE Users (id bigint(20) PRIMARY KEY COMMENT 用户ID,username varchar(255) NOT NULL COMMENT 用户名,password varchar(255) NOT NULL COMMENT 密码,status int(1) DE…...

如何使用Savitzky-Golay滤波器进行轨迹平滑
一、Savitzky-Golay滤波器介绍 Savitzky-Golay滤波器是一种数字滤波器,用于平滑数据,特别是在信号处理中。它基于最小二乘法的思想,通过拟合数据到一个滑动窗口内的低阶多项式来实现平滑。这种滤波器的优点是它可以保留数据的高频信息&#…...
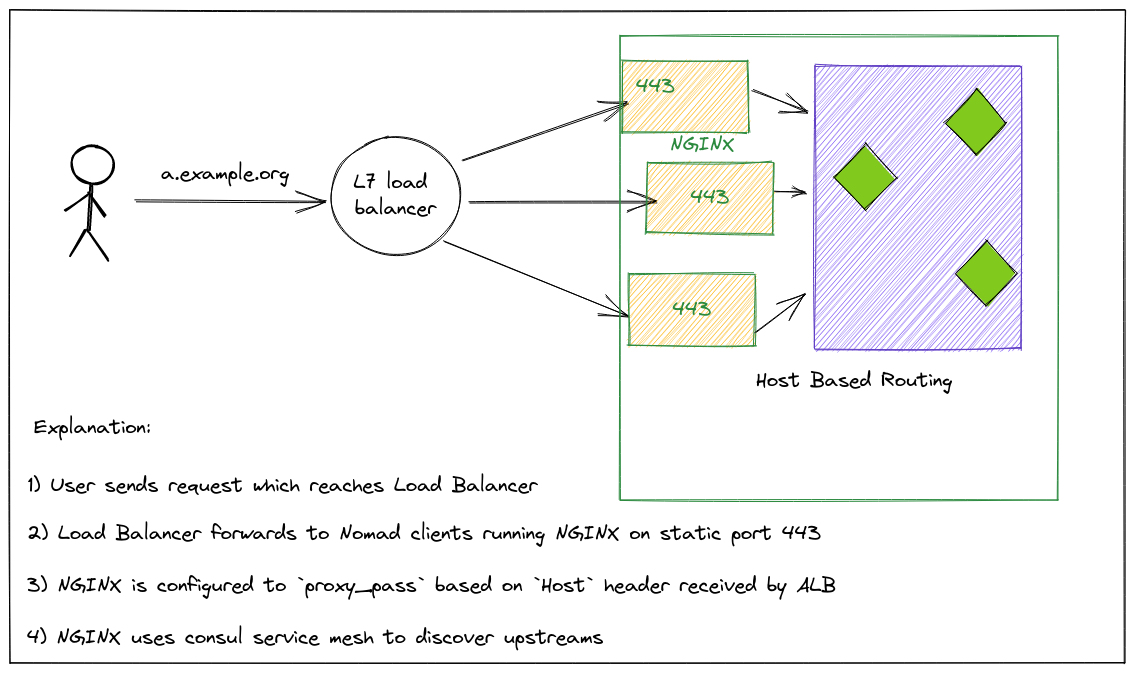
Nomad系列-Nomad网络模式
系列文章 Nomad 系列文章 概述 Nomad 的网络和 Docker 的也有很大不同, 和 K8s 的有很大不同. 另外, Nomad 不同版本(Nomad 1.3 版本前后)或是否集成 Consul 及 CNI 等不同组件也会导致网络模式各不相同. 本文详细梳理一下 Nomad 的主要几种网络模式 在Nomad 1.3发布之前&a…...

OpenCV项目开发实战--实现面部情绪识别对情绪进行识别和分类及详细讲解及完整代码实现
文末提供免费的完整代码下载链接 面部情绪识别(FER)是指根据面部表情对人类情绪进行识别和分类的过程。通过分析面部特征和模式,机器可以对一个人的情绪状态做出有根据的猜测。面部识别的这个子领域是高度跨学科的,借鉴了计算机视觉、机器学习和心理学的见解。 在这篇研究…...

Validate表单组件的封装
之前一直是直接去使用别人现成的组件库,也没有具体去了解人家的组件是怎么封装的,造轮子才会更好地提高自己,所以尝试开始从封装Form表单组件开始 一:组件需求分析 本次封装组件,主要是摸索封装组件的流程,…...

企业架构LNMP学习笔记32
企业架构LB-服务器的负载均衡之LVS实现: 学习目标和内容 1)能够了解LVS的工作方式; 2)能够安装和配置LVS负载均衡; 3)能够了解LVS-NAT的配置方式; 4)能够了解LVS-DR的配置方式&…...

基于Jetty9的Geoserver配置https证书
1.环境准备 由于Geoserver自带的jetty版本不具备https模块,所以需要下载完整版本jetty。这里需要先查看本地geoserver对应的jetty版本,进入geoserver安装目录,执行如下命令。 java -jar start.jar --version Jetty Server Classpath: -----…...

企业互联网暴露面未知资产梳理
一、互联网暴露面梳理的重要性 当前,互联网新技术的产生推动着各种网络应用的蓬勃发展,网络安全威胁逐渐蔓延到各种新兴场景中,揭示着网络安全威胁不断加速泛化。当前网络存在着许多资产,这些资产关系到企业内部的安全情况&#…...
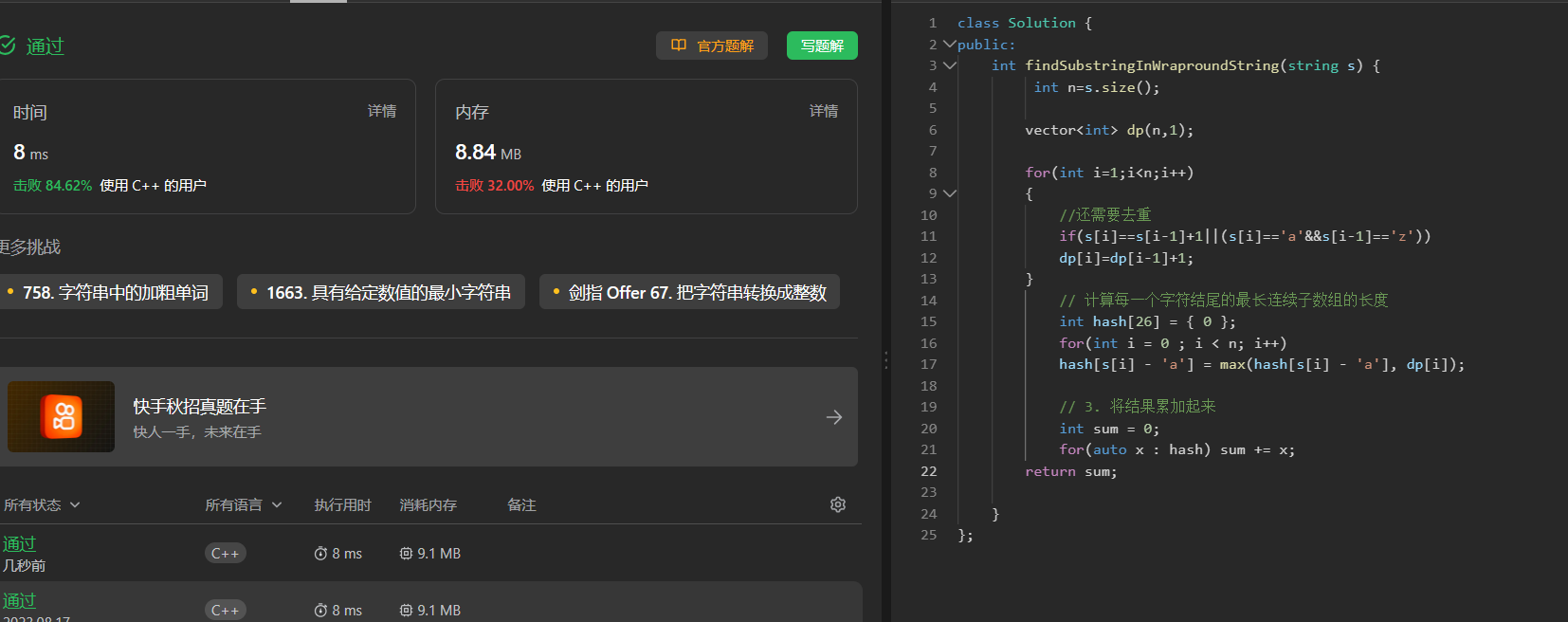
【动态规划刷题 12】等差数列划分 最长湍流子数组
139. 单词拆分 链接: 139. 单词拆分 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。 注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。 示例 1: 输入: …...

react-redux 的使用
react-redux React Redux 是 Redux 的官方 React UI 绑定库。它使得你的 React 组件能够从 Redux store 中读取到数据,并且你可以通过dispatch actions去更新 store 中的 state 安装 npm install --save react-reduxProvider React Redux 包含一个 <Provider…...

77 # koa 中间件的应用
调用 next() 表示执行下一个中间件 const Koa require("koa");const app new Koa();app.use(async (ctx, next) > {console.log(1);next();console.log(2); });app.use(async (ctx, next) > {console.log(3);next();console.log(4); });app.use(async (ctx,…...
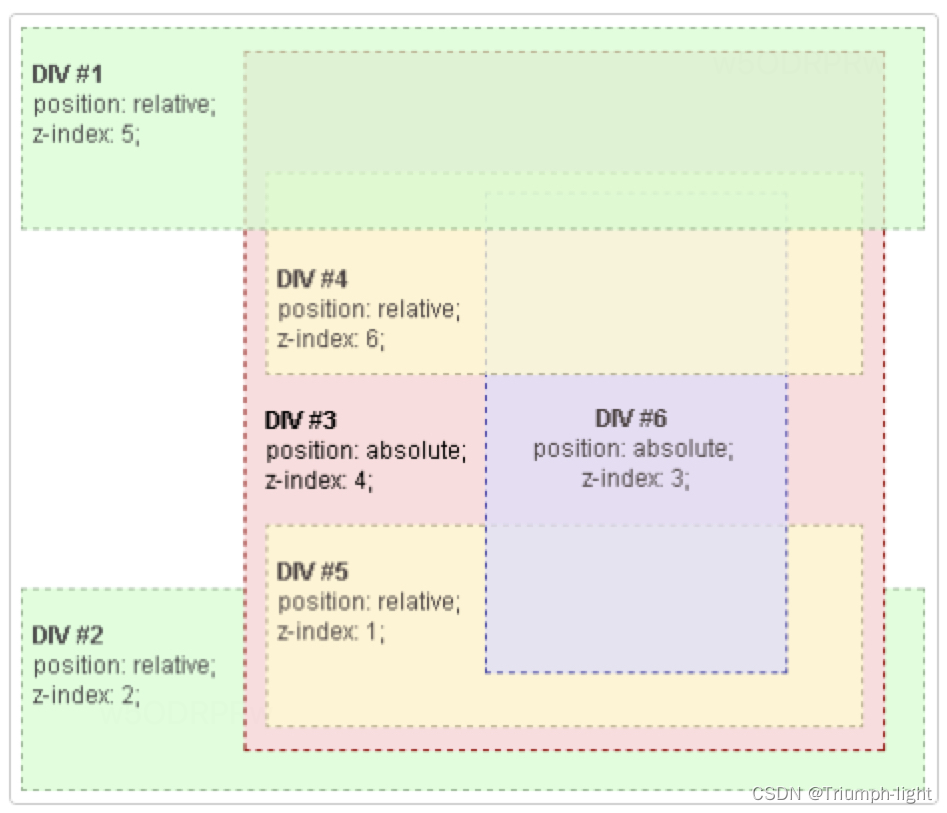
【css】z-index与层叠上下文
z-index属性用来设置元素的堆叠顺序,使用z-index有一个大的前提:z-index所作用元素的样式列表中必须有position属性并且属性值为absolute、relative或fixed中的一个,否则z-index无效。 层叠上下文 MDN讲解 我们给元素设置的z-index都是有一…...
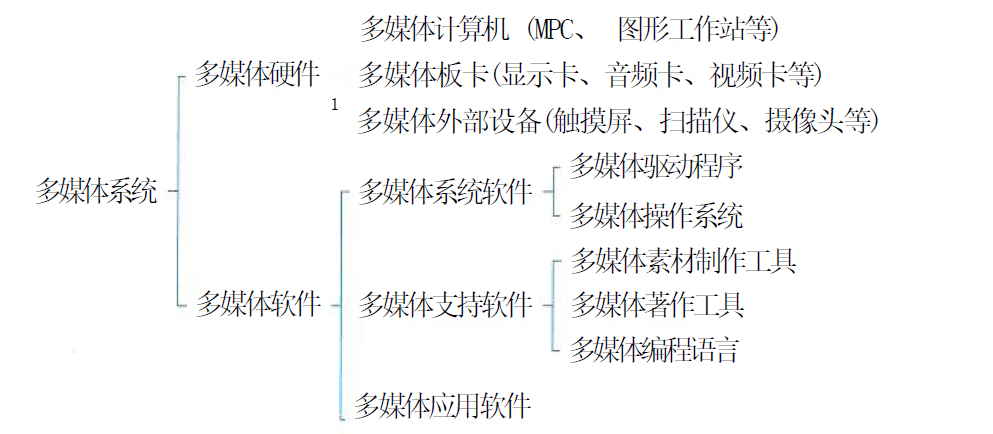
系统架构设计师(第二版)学习笔记----多媒体技术
【原文链接】系统架构设计师(第二版)学习笔记----多媒体技术 文章目录 一、多媒体概述1.1 媒体的分类1.2 多媒体的特征1.3 多媒体系统的基本组成 二、多媒体系统的关键技术2.1 多媒体系统的关键技术2.2 视频技术的内容2.3 音频技术的内容2.4 数据压缩算法…...
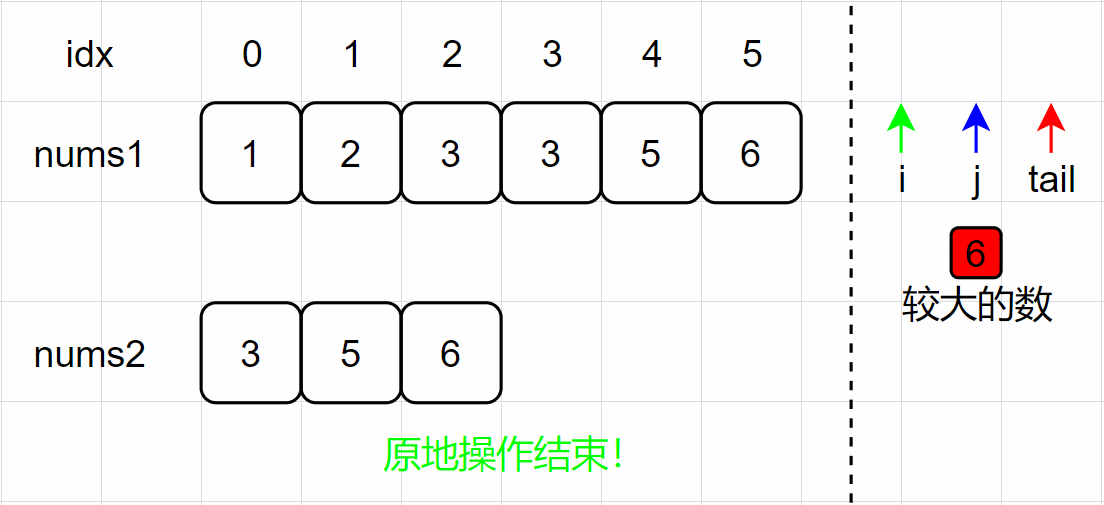
【面试经典150 | 数组】合并两个有序数组
文章目录 写在前面Tag题目来源题目解读解题思路方法一:合并排序方法二:双指针方法三:原地操作-从前往后方法四:原地操作-从后往前 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章…...

系统架构设计专业技能 ·操作系统
现在的一切都是为将来的梦想编织翅膀,让梦想在现实中展翅高飞。 Now everything is for the future of dream weaving wings, let the dream fly in reality. 点击进入系列文章目录 系统架构设计高级技能 操作系统 一、操作系统概述二、进程管理2.1 进程概念2.2 进…...

CSP 202209-1 如此编码
答题 题目就是字多 #include<iostream>using namespace std;int main() {int n,m;cin>>n>>m;int a[n],c[n1];c[0]1;for(int i0;i<n;i){cin>>a[i];c[i1]c[i]*a[i];}for(int i0;i<n;i){cout<<(m%c[i1]-m%c[i])/c[i]<< ;} }...
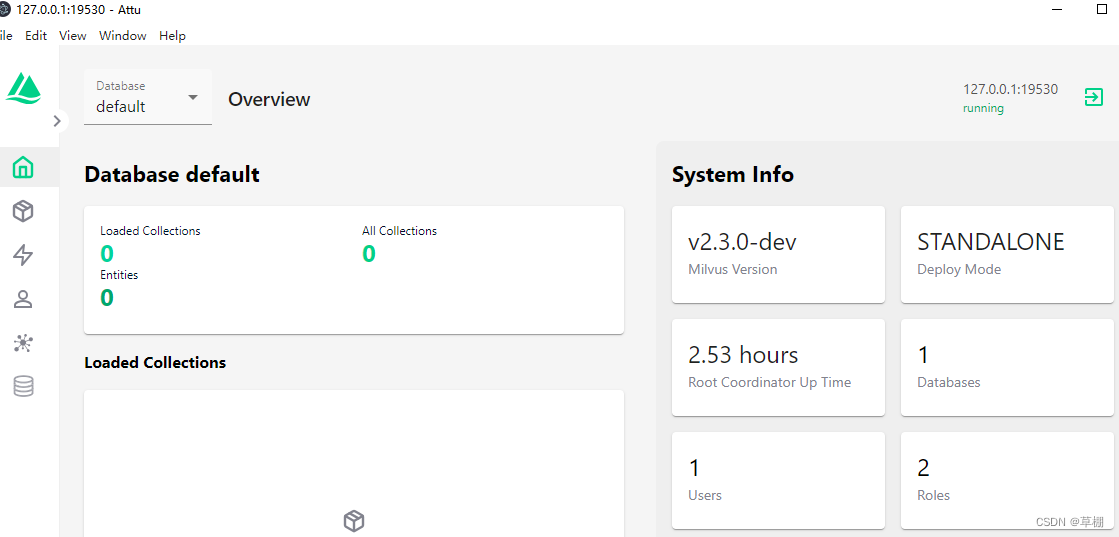
windows安装向量数据库milvus
本文介绍windows下安装milvus的方法。 一.Docker安装 1.1docker下载 首先到Docker官网上下载docker:Docker中文网 官网 1.2.安装前前期准备 先使用管理员权限打开windows powershell 然后在powershell里面输入下面那命令,启用“适用于 Linux 的 Windows 子系统”…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
