深度优先搜索遍历与广度优先搜索遍历
目录
一.深度优先搜索遍历
1.深度优先遍历的方法
2.采用邻接矩阵表示图的深度优先搜索遍历
3.非连通图的遍历
二.广度优先搜索遍历
1.广度优先搜索遍历的方法
2.非连通图的广度遍历
3.广度优先搜索遍历的实现
4.按广度优先非递归遍历连通图
一.深度优先搜索遍历
1.深度优先遍历的方法
从图中一个未访问的顶点V开始,沿着一条路一直走到底,如果到达这条路尽头的节点 ,则回退到上一个节点,再从另一条路开始走到底…,不断递归重复此过程,直到所有的顶点都遍历完成。
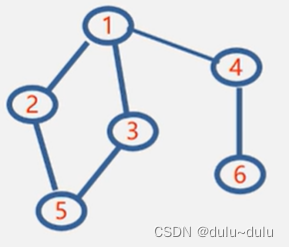
以下面无向图为例,2为起点
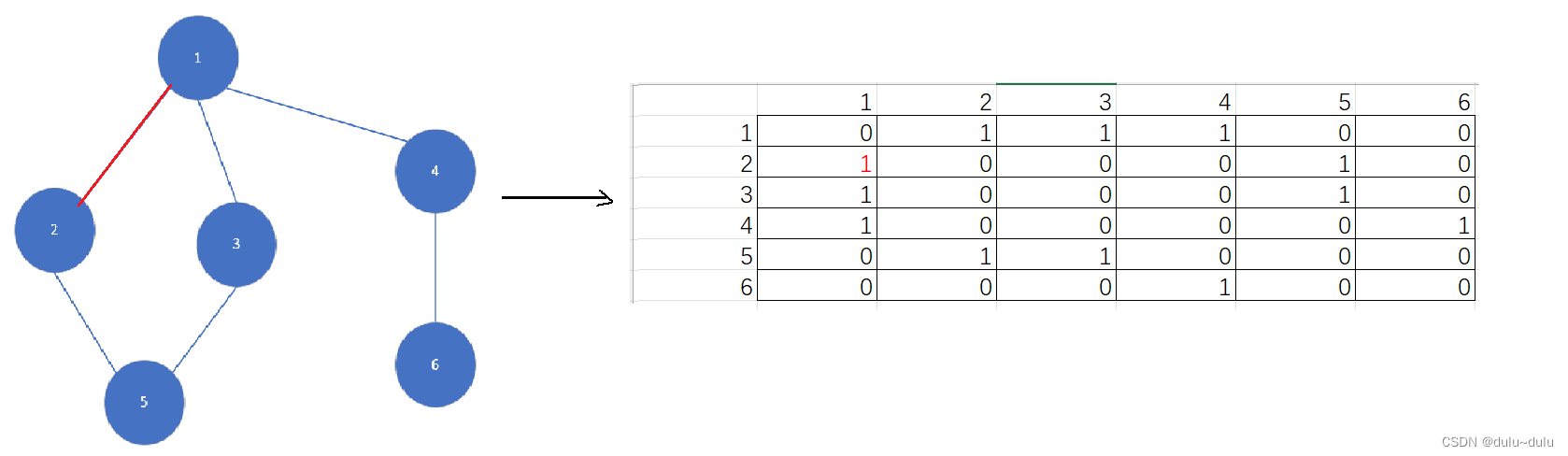
(1)以2为起点访问1
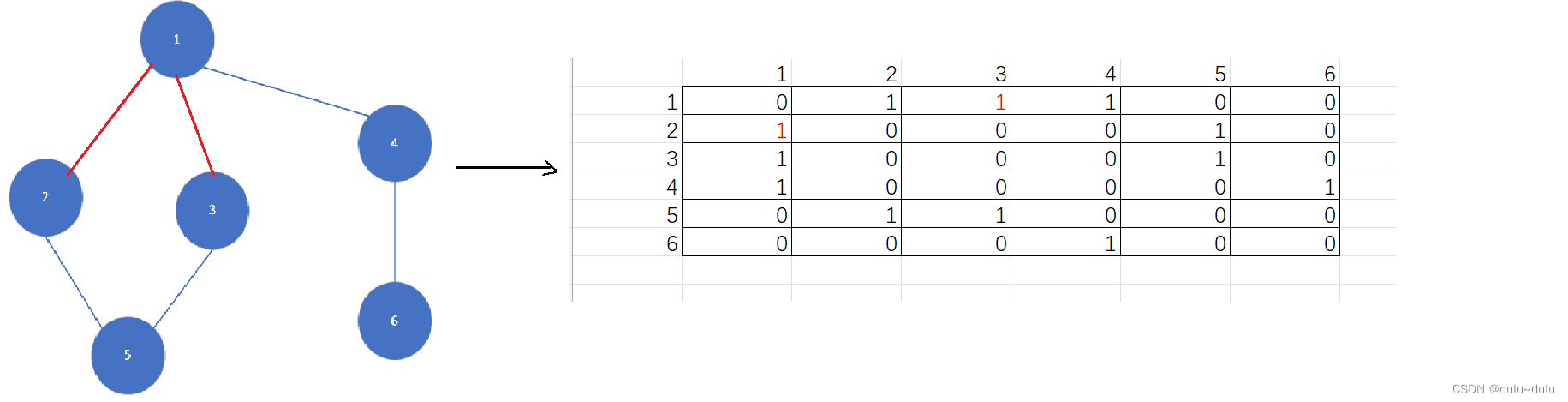
(2)以1为起点,因为“1”和“2”之间的边已经走过,所以走3
(3) 同理,以3为起点访问5
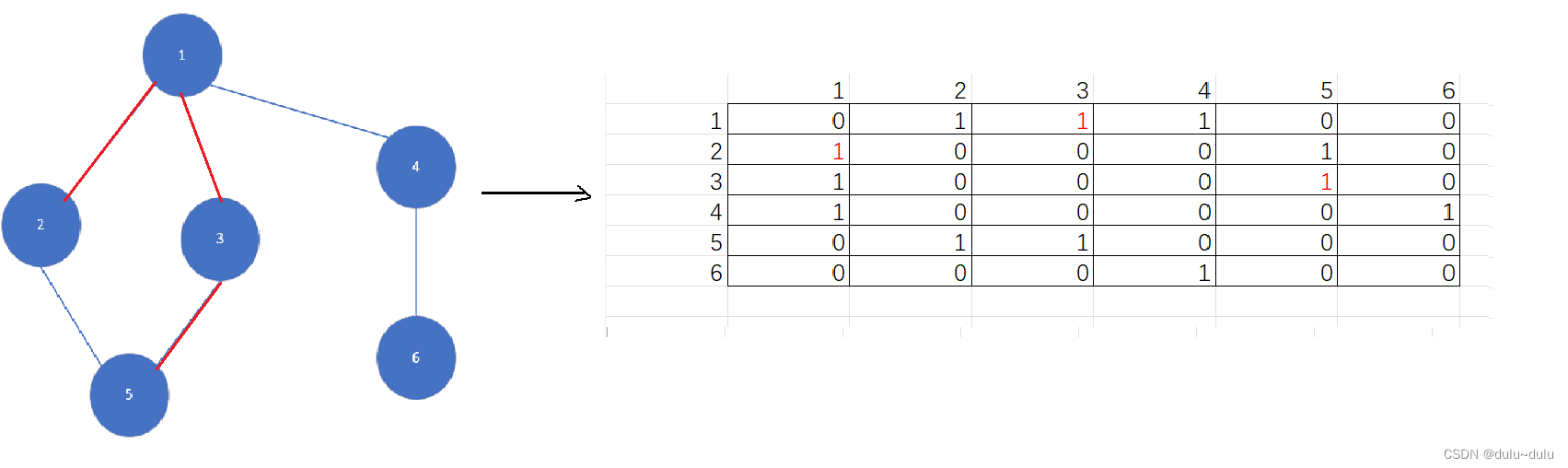
(4)到5后,没有可访问的点,返回3,3也没有可访问的点,到1后,可访问之前没有访问过的4
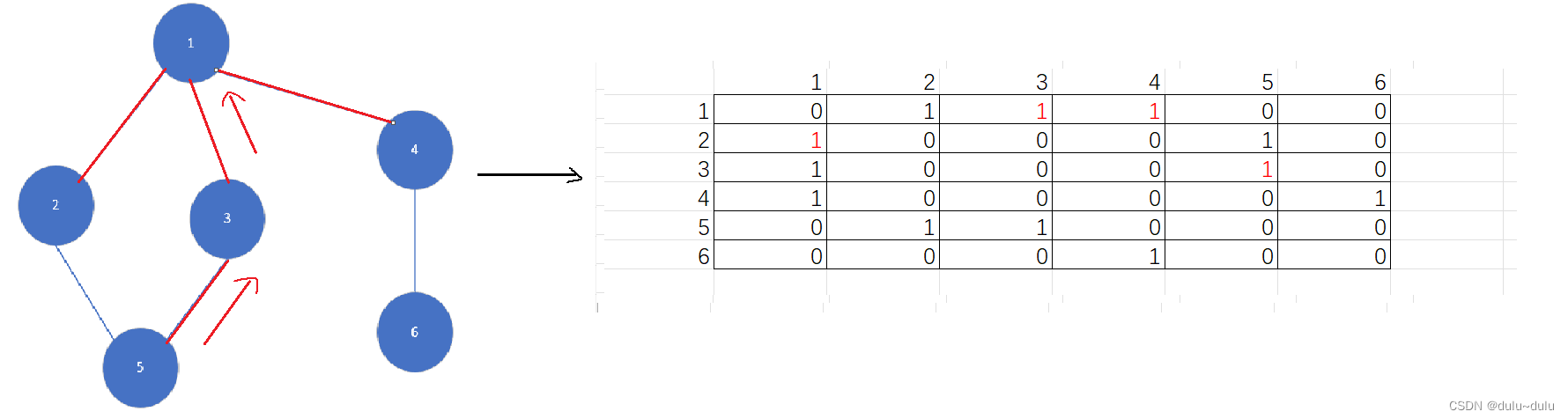
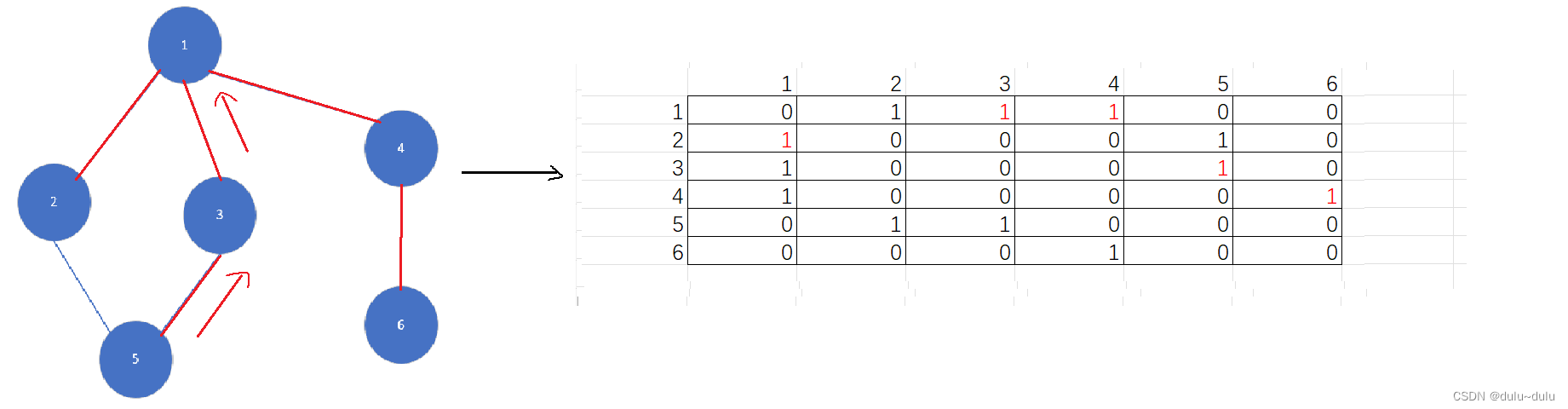
(5)4访问6,至此,遍历完所有的点,DFS(深度优先搜索遍历):2->1->3->5->4->6
2.采用邻接矩阵表示图的深度优先搜索遍历
#define MAX_VERTEX_NUM 100typedef struct {// 定义图的相关信息int vexnum; // 顶点数int arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 邻接矩阵// 其他成员...
} AMSGraph;bool visited[MAX_VERTEX_NUM]; // 记录顶点是否被访问过void DFS(AMSGraph G, int v)
{cout << v;visited[v] = true;for (int w = 0; w < G.vexnum; w++) {if (G.arcs[v][w] == 1 && !visited[w]) {DFS(G, w);}}
}http://t.csdn.cn/HmcOt
之前的一篇文章已经详细说明了邻接矩阵和邻接表的区别,这里同理
1.用邻接矩阵表示图,遍历图中每一个顶点都要从头扫描该顶点所在行,时间复杂度O(
)
2.用邻接表表示图,虽然有2e个表结点,但只需扫描e个结点即可完成遍历,加上访问n个头结点的时间,时间复杂度为O(n+e)
•稠密图适于在邻接矩阵上进行深度遍历;
•稀疏图适于在邻接表上进行深度遍历。
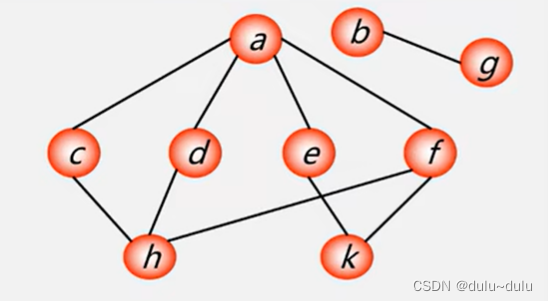
3.非连通图的遍历
左边的连通分量进行深度优先搜索遍历,再在b,g之中选择一个点进行深度优先搜索遍历
其中一种合理的顶点访问次序为:
a,c,h,d,f,k,e,b,g
二.广度优先搜索遍历
1.广度优先搜索遍历的方法
从某个顶点V出发,访问该顶点的所有邻接点V1,V2..VN,从邻接点V1,V2...VN出发,再访问他们各自的所有邻接点,重复上述步骤,直到所有的顶点都被访问过
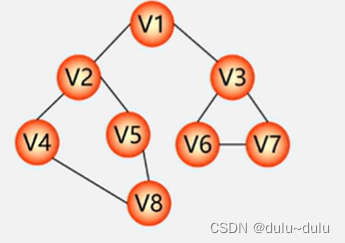
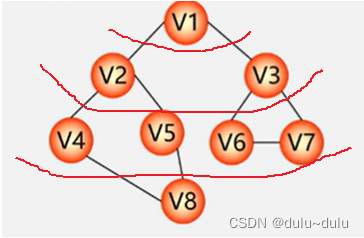
以如下图为例,起点为V1
一层一层进行访问,广度优先搜索遍历的结果为:V1->C2->V3->V4->V5->V6->V7->V8
2.非连通图的广度遍历
与连通图类似,在b,g中任意选择一个点开始
合理的顶点访问次序为:a->c->d->e->f->h->k->b->g

3.广度优先搜索遍历的实现
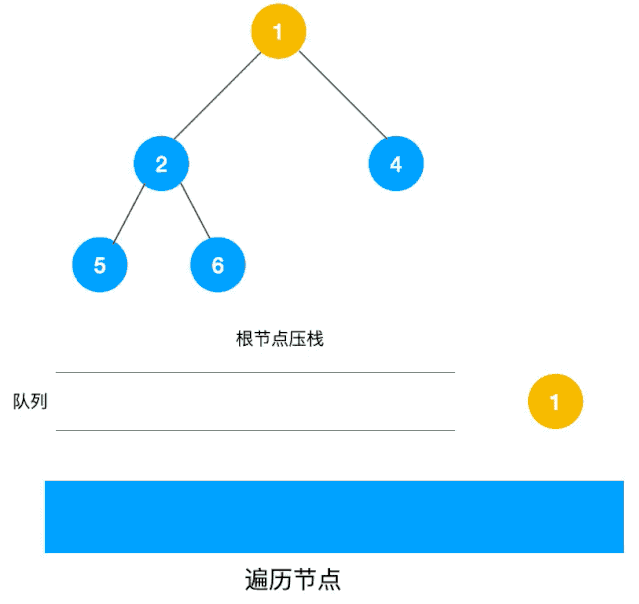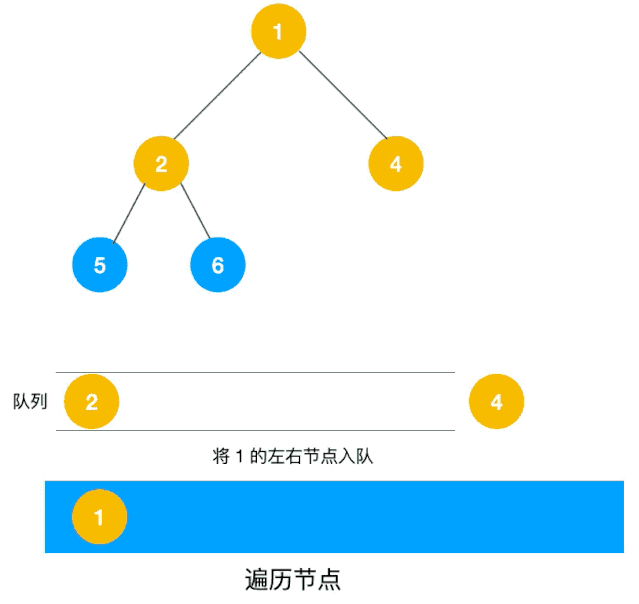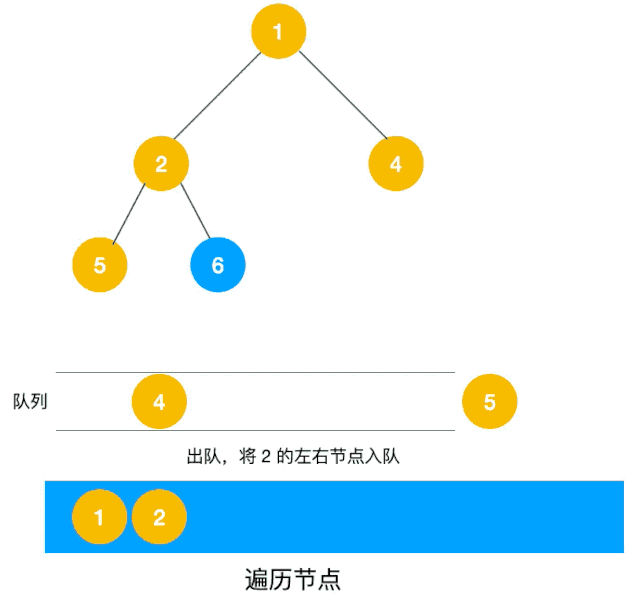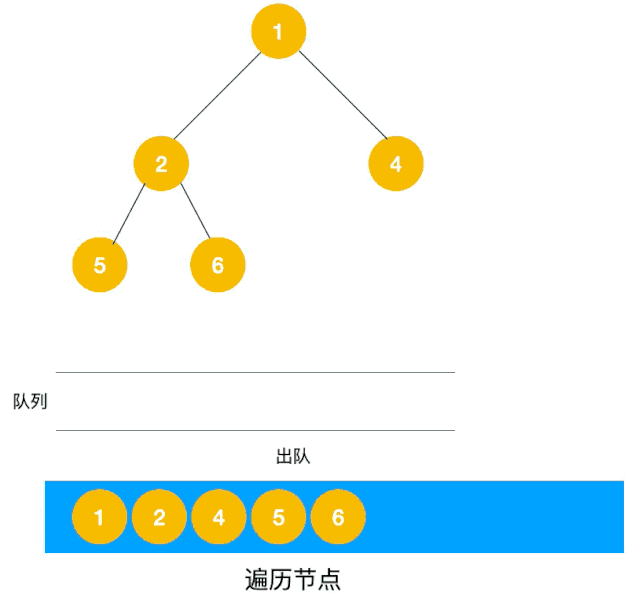
广度优先搜索遍历的实现,与树的层次遍历很像,可以用队列进行实现(出队一个结点,将他的邻接结点入队)
以下动图来自爱编程的西瓜,方便大家理解遍历过程
4.按广度优先非递归遍历连通图
#include <iostream>
using namespace std;const int MAX_SIZE = 100; // 队列的最大容量
const int MAX_VERTICES = 100; // 图的最大顶点数struct Queue {int data[MAX_SIZE];int front; // 队头指针int rear; // 队尾指针
};struct Graph { // 定义图bool edges[MAX_VERTICES][MAX_VERTICES]; // 邻接矩阵int numVertices; // 实际顶点数
};void InitQueue(Queue& Q) {Q.front = 0;Q.rear = -1;
}bool EnQueue(Queue& Q, int x) {if (Q.rear == MAX_SIZE - 1) {// 队列已满,无法插入return false;}Q.data[++Q.rear] = x;return true;
}bool DeQueue(Queue& Q, int& x) {if (Q.front > Q.rear) {// 队列为空,无法出队return false;}x = Q.data[Q.front++];return true;
}bool QueueEmpty(Queue& Q) {return Q.front > Q.rear;
}// 找到顶点u的第一个邻接点并返回
int FirstAdjVex(Graph& G, int u) {for (int v = 0; v < G.numVertices; ++v) {if (G.edges[u][v]) {return v;}}return -1; // 或者返回一个特殊的值表示找不到邻接点
}// 找到图 G 中顶点 u 相对于顶点 w 的下一个邻接点并返回
int NextAdjVex(Graph& G, int u, int w) {for (int v = w + 1; v < G.numVertices; ++v) {if (G.edges[u][v]) {return v;}}return -1; // 或者返回一个特殊的值表示找不到下一个邻接点
}void BFS(Graph G, int v) {cout << v;bool visited[MAX_VERTICES] = { false };visited[v] = true; // 访问第v个顶点Queue Q;InitQueue(Q);EnQueue(Q, v); // v进队while (!QueueEmpty(Q)) {int u;DeQueue(Q, u); // 队头元素出队并置为ufor (int w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w)) {if (!visited[w]) { // w为u的尚未访问的邻接点cout << w;visited[w] = true;EnQueue(Q, w); // w进队(将访问的每一个邻接点入队)}}}
}
广度优先搜索遍历算法的效率
1.如果使用邻接矩阵,则BFS对于每一个被访问到的顶点,都要循环检测矩阵中的整整一行,时间复杂度为O()
2.用邻接表来表示图,虽然有2e个表结点,但只需扫描e个结点即可完成遍历,加上访问n个头结点的实践,时间复杂度为O(n+e)
深度优先搜索遍历(DFS)与广度优先搜索遍历(BFS)算法的效率
1.空间复杂度相同,都是O(n)(借用了堆栈或队列)
2.时间复杂度只与存储结构(邻接矩阵【O()】或邻接表【O(n+e)】)有关,而与搜索路径无关
相关文章:
深度优先搜索遍历与广度优先搜索遍历
目录 一.深度优先搜索遍历 1.深度优先遍历的方法 2.采用邻接矩阵表示图的深度优先搜索遍历 3.非连通图的遍历 二.广度优先搜索遍历 1.广度优先搜索遍历的方法 2.非连通图的广度遍历 3.广度优先搜索遍历的实现 4.按广度优先非递归遍历连通图 一.深度优先搜索遍历 1.深…...

java 中 返回一个空Map
原文链接:Map用法总结 Constructs an empty HashMap with the default initial capacity (16) (mutable) // Constructs an empty HashMap with the default initial capacity (16) and the default load fact // Since:1.2 Map<String, …...

sql 执行插入多条语句中 n个insert 与 一个insert+多个values 性能上有和区别 -- chatGPT
在 SQL 中,你可以使用多种方式来插入多条记录。其中两种常见的方式是: 1. **多个 INSERT 语句**:每个 INSERT 语句都插入一行记录。 sql INSERT INTO table_name (column1, column2, ...) VALUES (value1_1, value1_2, ...); INSERT INTO …...

数学建模国赛C蔬菜类商品的自动定价与补货决策C
数学建模国赛C蔬菜类商品的自动定价与补货决策C 完整思路和代码请私信~~~ 1.拟解决问题 这是一个关于生鲜商超蔬菜商品管理的复杂问题,需要综合考虑销售、补货、定价等多个方面。以下是对这些问题的总结: 问题 1: 蔬菜销售分析 需要分析蔬菜各品类和…...
的重要性)
在程序开发中,接口(interface)的重要性
开了很多人写的程序,都适用了接口,也适用了注入,也没有感到什么不妥。如果只是为了注入而写接口,其实我感觉大可不必,特别是把接口和实体写在一个项目项目中的。 我不知道其他人怎么看接口这一层,接口最大的…...

MyBatis关联关系映射详解
前言 在使用MyBatis进行数据库操作时,关联关系映射是一个非常重要的概念。它允许我们在数据库表之间建立关联,并通过对象之间的关系来进行数据查询和操作。本文将详细介绍MyBatis中的关联关系映射,包括一对一、一对多和多对多关系的处理方法…...
常用电子元器件基础知识
目录 一、电阻 二、电容 三、电感 四、保险丝 五、二极管 一、电阻 概念:顾名思义,就是增加电流通过的阻力的。 就像是在水渠中放入东西,能阻止水的顺利通过也是一个道理。 基于电阻的电气特性,电阻在电路中主要有以下四个…...
git撤销还未push的的提交
怎样撤销掉上图中的提交呢 使用以下代码即可提交 git reset --soft HEAD^...

MySQL--数据库基础
数据库分类 数据库大体可以分为 关系型数据库 和 非关系型数据库 常用数据类型 数值类型: 分为整型和浮点型: 字符串类型 日期类型...
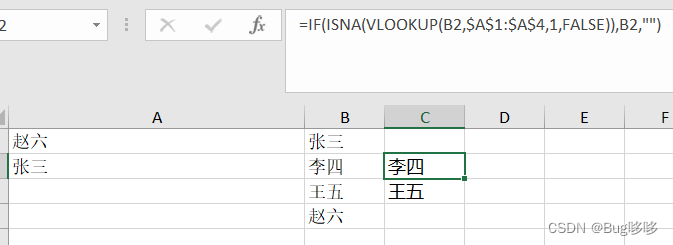
Excel相关笔记
1、找出B列中A列没有的数据并放在C列 公式:IF(ISNA(VLOOKUP(B1,$A 1 : 1: 1:A$4,1,FALSE)),B1,“”)...
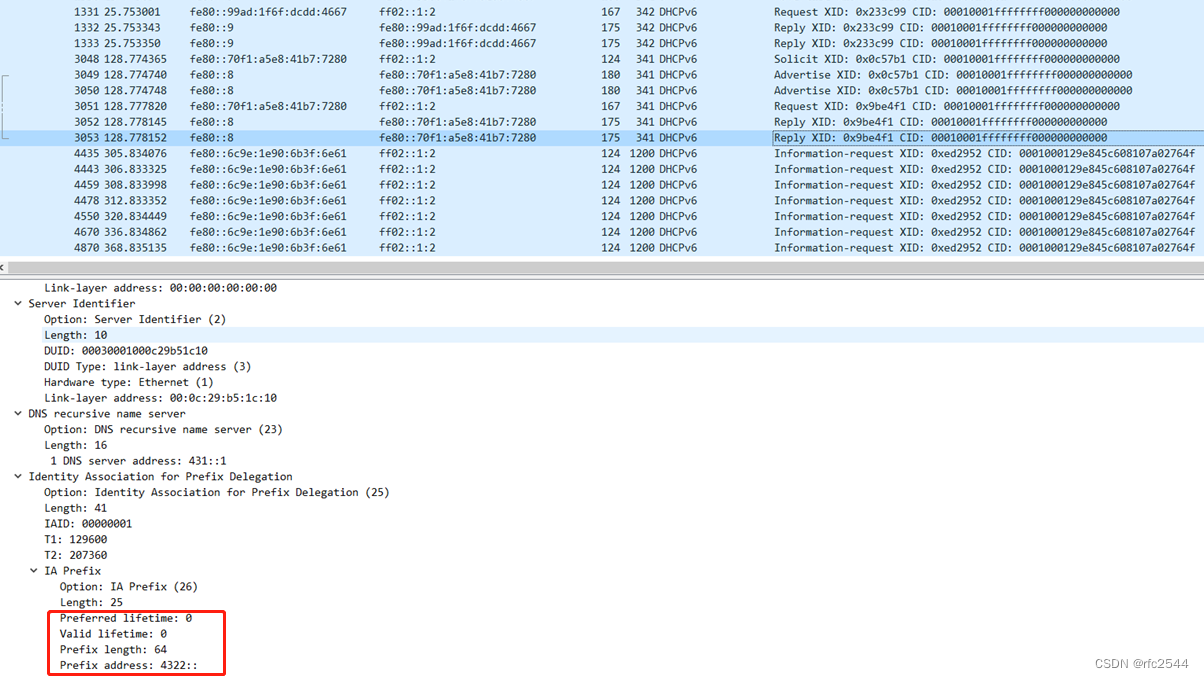
RouterOS-配置PPPoEv4v6 Server
1 接口 ether3 出接口 ether4 内网接口 2 出接口 出接口采用PPPoE拨号SLAAC获取前缀,手动配置后缀 2.1 选择出接口interface,配置PPPoE client模式 2.2 配置PPPoE client用户名和密码 2.3 从PPPoE client获取前缀地址池 2.4 给出接口选择前缀并配置…...

PhpStorm软件安装包分享(附安装教程)
目录 一、软件简介 二、软件下载 一、软件简介 PhpStorm是一款由JetBrains开发的专业PHP集成开发环境(IDE),旨在提供全面的PHP开发支持。它是基于IntelliJ IDEA平台构建的,具有强大的功能和工具,可以帮助开发人员提高…...

JavaScript设计模式(三)——单例模式、装饰器模式、适配器模式
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 📃个人状态: 研发工程师,现效力于中国工业软件事业 🚀人生格言: 积跬步…...

LeetCode:有序数组的平方
题目 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输入:nums [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组变…...

数学分析:势场
首先从散度的物理解释开始。首先,在球内的向量场的散度的积分,等于它在球边界上的流量的积分。所以根据积分中值定理,我们可以这么理解散度,它就是这个体积内的速度场的平均密度。而速度场只和源有关,所以它表示的某个…...

MySQL 中 MyISAM 与 InnoDB 引擎的区别
分析&回答 区别很多,大家说出下面几点,面试就应该 OK 了 1) 事务支持 MyISAM不支持事务,而InnoDB支持。InnoDB的AUTOCOMMIT默认是打开的,即每条SQL语句会默认被封装成一个事务,自动提交,这样会影响速…...
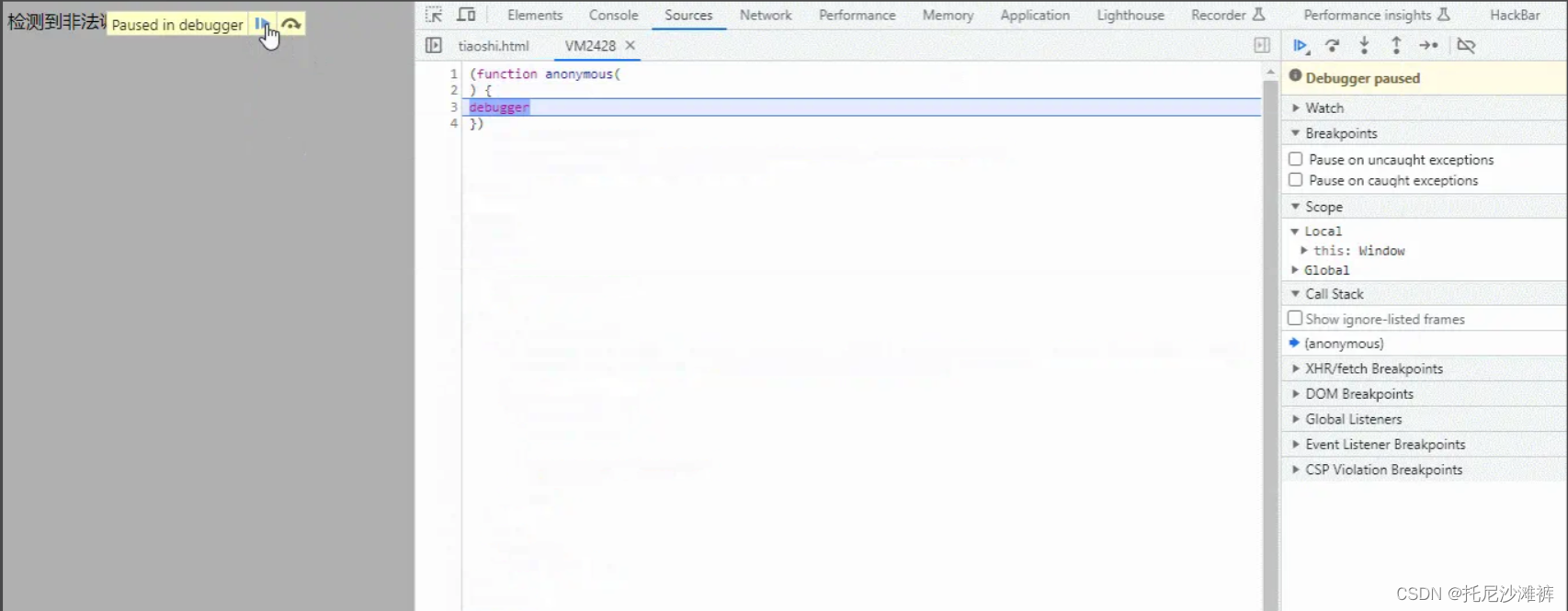
【javascript】禁止浏览器调试前端页面
目录 为啥要禁止?无限 debugger基础禁止调试解决对策 为啥要禁止? 由于前端页面会调用很多接口,有些接口会被别人爬虫分析,破解后获取数据,为了杜绝这种情况,最简单的方法就是禁止人家调试自己的前端代码 …...
 的过程)
Oracle Non-CDB配置 TDE(透明数据加密) 的过程
说明 此文档虽然是针对non CDB而写,但是对于CDB的操作过程也是类似的,即在CDB$ROOT中设置完成wallet设置后,在PDB中设置和打开MEK即可。 先决条件 请确保目录$ORACLE_SID/admin/$ORACLE_SID存在,例如此目录为: /u01/app/oracl…...

MySQL——常见问题
NULL和空值的区别 1、空值不占空间,NULL值占空间。当字段不为NULL时,也可以插入空值。 2、当使用 IS NOT NULL 或者 IS NULL 时,只能查出字段中没有不为NULL的或者为 NULL 的,不能查出空值。 3、判断NULL 用IS NULL 或者 is no…...
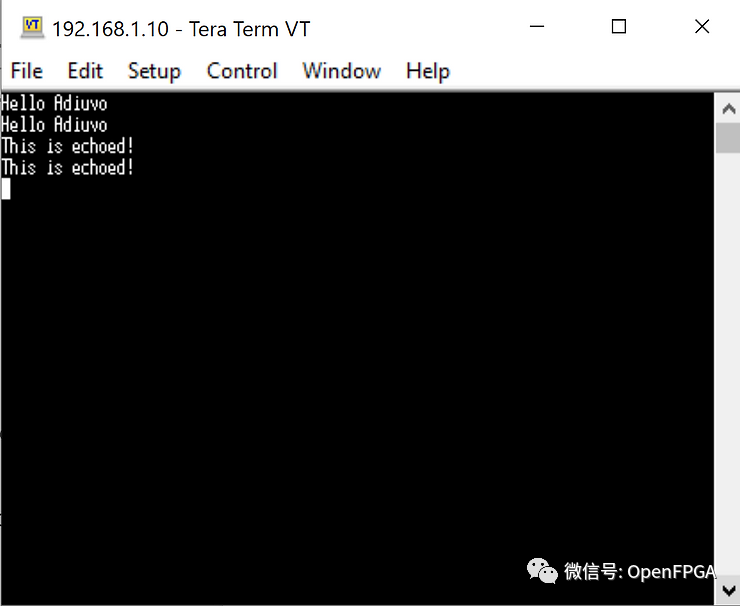
在FPGA上快速搭建以太网
在本文中,我们将介绍如何在FPGA上快速搭建以太网 (LWIP )。为此,我们将使用 MicroBlaze 作为主 CPU 运行其应用程序。 LWIP 是使用裸机设计以太网的良好起点,在此基础上我们可以轻松调整软件应用程序以提供更详细的应用…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...