c++ 学习之 静态成员变量和静态成员函数
文章目录
- 前言
- 正文
- 静态成员变量
- 初始化操作
- 如何理解共享一份数据
- 访问权限
- 静态成员函数
- 访问方式
- 静态成员函数只能访问静态成员变量
- 访问权限
前言
静态成员分为
1)静态成员变量
- 所有对象共享一份数据
- 在编译阶段分配空间
- 类内声明,类外初始化
2)静态成员函数 - 所有对象共享一个函数
- 静态成员函数只能访问静态成员变量
正文
静态成员变量
初始化操作
- 静态变量要进行初始化操作,不然使用的时候会报错
我们来看看下面的代码:
#define CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;class Person {
public:static int m_A;};void test()
{Person p;cout << p.m_A << endl;
}int main()
{test();
}
上面的代码会报错,因为调用 p.m_A 的时候由于它没有被赋初值,所以会报错
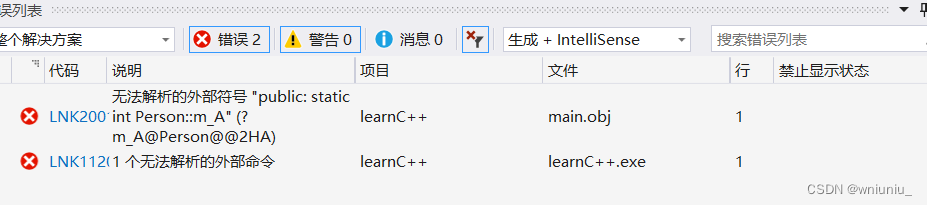
那怎么解决这个问题呢?
可以在类内初始化吗?
答案是不可以
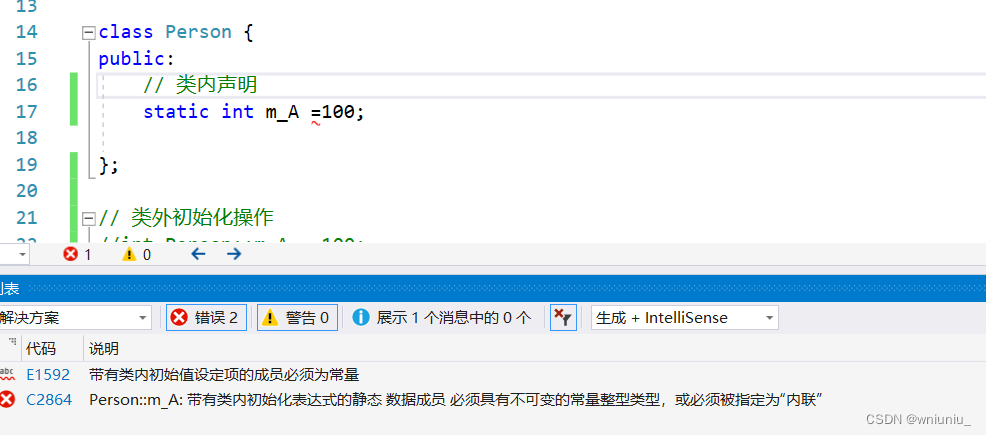
那究竟该如何初始化呢
我们要在类外初始化

这样就解决问题了
如何理解共享一份数据
看完下面这个代码和运行结果你就会了解了
#define CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;// 静态成员分为
// 1)静态成员变量
// * 所有对象共享一份数据
// * 在编译阶段分配空间
// * 类内声明,类外初始化
// 2)静态成员函数
// * 所有对象共享一个函数
// * 静态成员函数只能访问静态成员变量class Person {
public:// 类内声明static int m_A ;};// 类外初始化操作
int Person::m_A = 100;void test()
{Person p;cout << p.m_A << endl;// 再实例化一个对象Person B;cout << B.m_A << endl;B.m_A = 200;cout << p.m_A << endl;cout << B.m_A << endl;
}int main()
{test();
}
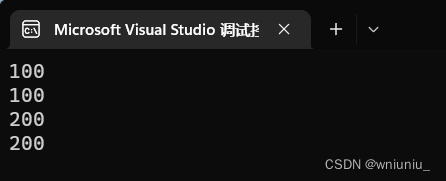
静态成员变量的访问方式有两种
#define CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;// 静态成员分为
// 1)静态成员变量
// * 所有对象共享一份数据
// * 在编译阶段分配空间
// * 类内声明,类外初始化
// 2)静态成员函数
// * 所有对象共享一个函数
// * 静态成员函数只能访问静态成员变量class Person {
public:// 类内声明static int m_A ;};// 类外初始化操作
int Person::m_A = 100;void test()
{Person p;cout << p.m_A << endl;// 再实例化一个对象Person B;cout << B.m_A << endl;B.m_A = 200;cout << p.m_A << endl;cout << B.m_A << endl;
}void test02()
{// 静态成员变量 不属于某个对象上,所有对象都共享同一份对象// 因此静态成员变量有两种访问方式// 1.通过对象进行访问Person p;cout << p.m_A << endl;// 2.通过类名进行访问cout << Person::m_A << endl;
}int main()
{//test();test02();
}
访问权限
如果静态成员变量是在 private 属性的,那么类外无法访问

在类外中 m_B 无法被访问
静态成员函数
访问方式
有两种访问方式
#define CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;// 静态成员分为
// 1)静态成员变量
// * 所有对象共享一份数据
// * 在编译阶段分配空间
// * 类内声明,类外初始化
// 2)静态成员函数
// * 所有对象共享一个函数
// * 静态成员函数只能访问静态成员变量class Person
{
public:// 静态成员函数static void fun(){cout << " static void fun 函数 调用 " << endl;}
};// 有两种访问方式
void test01()
{// 1.通过对象访问Person p;p.fun();// 2.通过类名访问Person::fun();
}int main()
{test01();
}
静态成员函数只能访问静态成员变量
class Person
{
public:// 静态成员函数static void fun(){cout << " static void fun 函数 调用 " << endl;m_A = 100; //(正确) 静态成员函数可以访问 静态成员函数m_B = 100; // (错误) 静态成员函数不可以访问 非静态成员函数,无法区分是哪个实例的 m_B}static int m_A; //静态成员变量int m_B; // 非静态成员变量
};
int Person::m_A = 10;
访问权限
如果静态成员函数是 private 权限下的,外部也不能访问
相关文章:

c++ 学习之 静态成员变量和静态成员函数
文章目录 前言正文静态成员变量初始化操作如何理解共享一份数据访问权限 静态成员函数访问方式静态成员函数只能访问静态成员变量访问权限 前言 静态成员分为 1)静态成员变量 所有对象共享一份数据在编译阶段分配空间类内声明,类外初始化 2)…...

C程序需要按下回车键才能读取字符
当编写涉及从终端输入字符的C程序时,有时会遇到需要按下回车键才能读取字符的问题。这是因为默认情况下,终端通常处于行缓冲模式,需要等待用户按下回车键才会将输入的字符发送给正在运行的程序。这可能会导致一些不便,尤其是当程序…...

x86体系结构(WinDbg学习笔记)
寄存器 eaxAccumulator累加器ebxBase register基寄存器ecxCounter register计数器寄存器edxData register - can be used for I/O port access and arithmetic functions数据寄存器-可用于I/O端口访问和算术函数esiSource index register源索引寄存器ediDestination index reg…...
Hadoop的第二个核心组件:MapReduce框架第四节
Hadoop的第二个核心组件:MapReduce框架 十、MapReduce的特殊应用场景1、使用MapReduce进行join操作2、使用MapReduce的计数器3、MapReduce做数据清洗 十一、MapReduce的工作流程:详细的工作流程第一步:提交MR作业资源第二步:运行M…...

算法通关村第十九关——最少硬币数
LeetCode322.给你一个整数数组 coins,表示不同面额的硬币,以及一个整数 amount,表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回-1。你可以认为每种硬币的数量是无限的。 示例1&…...
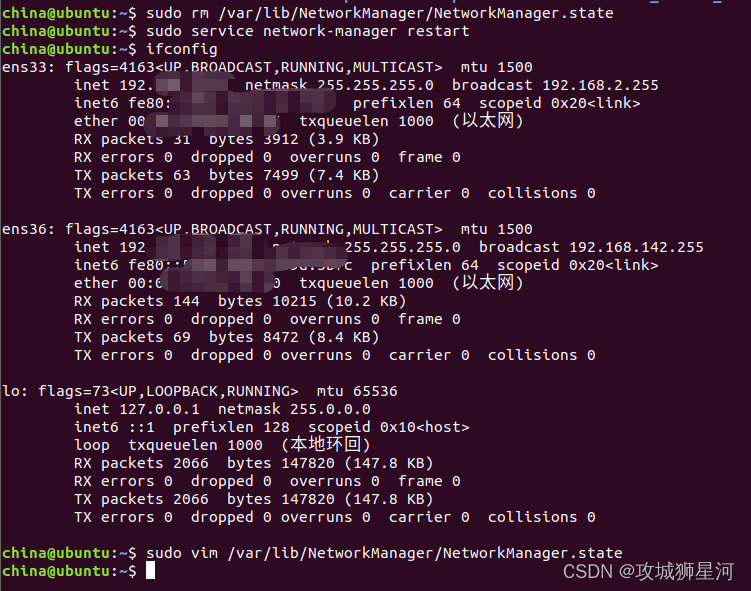
Linux ifconfig只显示 lo 网卡,没有ens网卡解决方案
项目场景: 虚拟机中linux无网络问题 问题描述 之前在调试linux的时候,由于一些不太清楚的误操作,导致ubuntu linux出现无网络问题,现象如下 ifconfig 只显示了 lo 网卡 lo 网卡:它是本地环回接口。 这意味着您的虚…...

Java复习-26-枚举
枚举(替换多例设计) 目的(使用场景) 不用也没啥 定义一个描述性别的类,那么该对象只有两个:男、 女。或者描述颜色基色的类,可以使用: 红色、绿色、蓝色。 功能 用于定义有限个数对象的一种结构&#x…...

NLP(六十八)使用Optimum进行模型量化
本文将会介绍如何使用HuggingFace的Optimum,来对微调后的BERT模型进行量化(Quantization)。 在文章NLP(六十七)BERT模型训练后动态量化(PTDQ)中,我们使用PyTorch自带的PTDQ&…...

Tomcat多实例和负载均衡动静分离
目录 一、Tomcat多实例部署 二、负载均衡动静分离 2.1.动静分离 2.11 nginx负载均衡 192.168.30.203 2.22 Tomcat服务器:192.168.30.200:80 2.23 Tomcat服务器:192.168.30.100:80 2.24 配置nginx 192.168.30.203静态页面 2…...
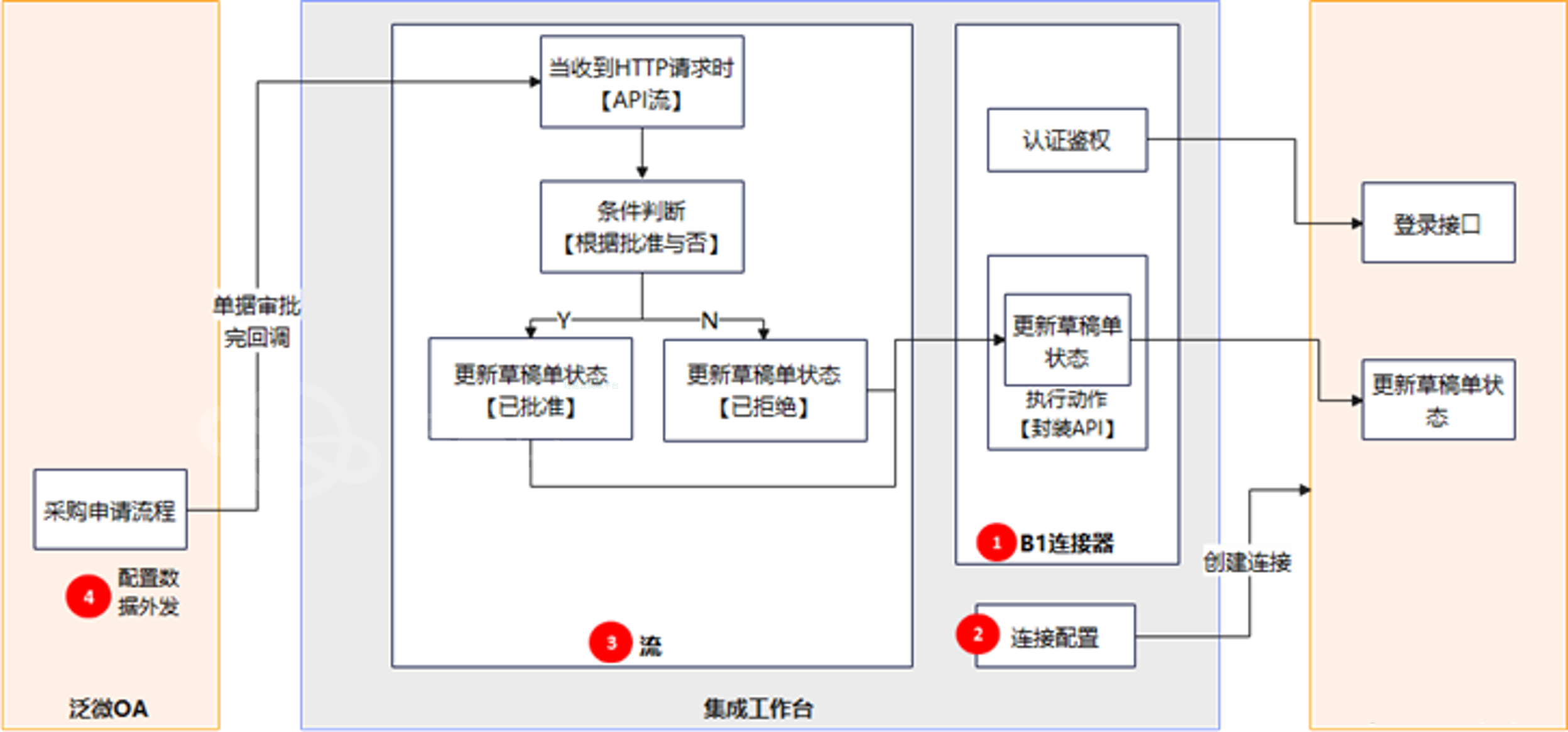
企业ERP和泛微OA集成场景分析
轻易云数据集成平台(qeasy.cloud)为企业ERP和泛微OA系统提供了强大的互通解决方案,特别在销售、采购和库存领域的单据审批场景中表现出色。这些场景涉及到多个业务单据的创建和审批,以下是一些具体的应用场景描述: 采购…...
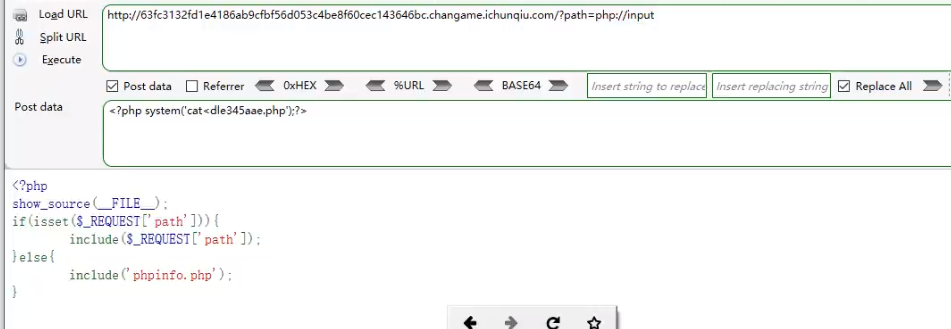
31 WEB漏洞-文件操作之文件包含漏洞全解
目录 文件包含漏洞原理检测类型利用修复 本地包含-无限制,有限制远程包含-无限制,有限制各种协议流玩法文章介绍读取文件源码用法执行php代码用法写入一句话木马用法每个脚本支持的协议玩法 演示案例某CMS程序文件包含利用-黑盒CTF-南邮大,i春…...

qmake.exe xxx.pro -spec win32-g++ 作用
作用 qmake.exe xxx.pro -spec win32-g的作用是使用win32-g构建系统规范来生成针对xxx.pro项目的构建脚本。 具体来说,这个命令的含义如下: qmake.exe:使用qmake命令行工具。xxx.pro:指定了要构建的项目文件,.pro文…...

SpringMVC实现增删改查
文章目录 一、配置文件1.1 导入相关pom依赖1.2 jdbc.properties:配置文件1.3 generatorConfig.xml:代码生成器1.4 spring-mybatis.xml :spring与mybatis整合的配置文件1.5 spring-context.xml :上下文配置文件1.6 spring-mvc-xml:…...
)
React 配置别名 @ ( js/ts 项目中通过 webpack.config.js 配置)
一、简介 在 Vue 项目当中,可以使用 来表示 src/,但在 React 项目中,默认却没有该功能,因此需要进行手动的配置来实现该功能。 别名主要解决的问题:每个页面都使用路径的方式进行引入,这样很麻烦ÿ…...
Android 在TextView前面添加多个任意View且不影响换行
实现效果如下: 如上,将头像后面的东西看作一个整体,因为不能影响后面内容的换行,且前面控件的长度是可变的,所以采用自定义View的方法来实现: /*** CSDN深海呐 https://blog.csdn.net/qq_40945489/articl…...

字符串相加
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。 你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。 示例 1: 输入ÿ…...

uni-app直播从0到1实战
1.安装开发工具 2.创建项目 参考:uniapp从零到一的学习商城实战_云澜哥哥的博客-CSDN博客...
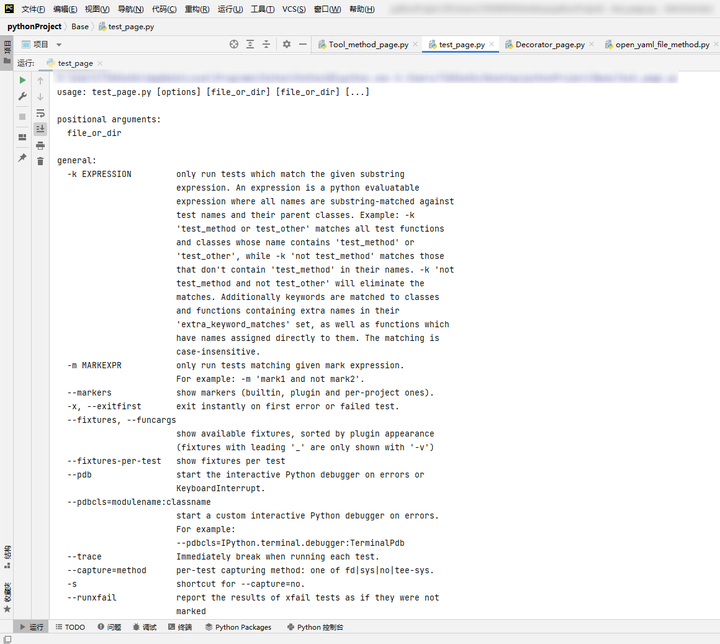
Python UI自动化 —— pytest常用运行参数解析、pytest执行顺序解析
pytest常用Console参数: -v 用于显示每个测试函数的执行结果-q 只显示整体测试结果-s 用于显示测试函数中print()函数输出-x 在第一个错误或失败的测试中立即退出-m 只运行带有装饰器配置的测试用例-k 通过表达式运行指定的测试用例-h 帮助 首先来看什么参数都没加…...
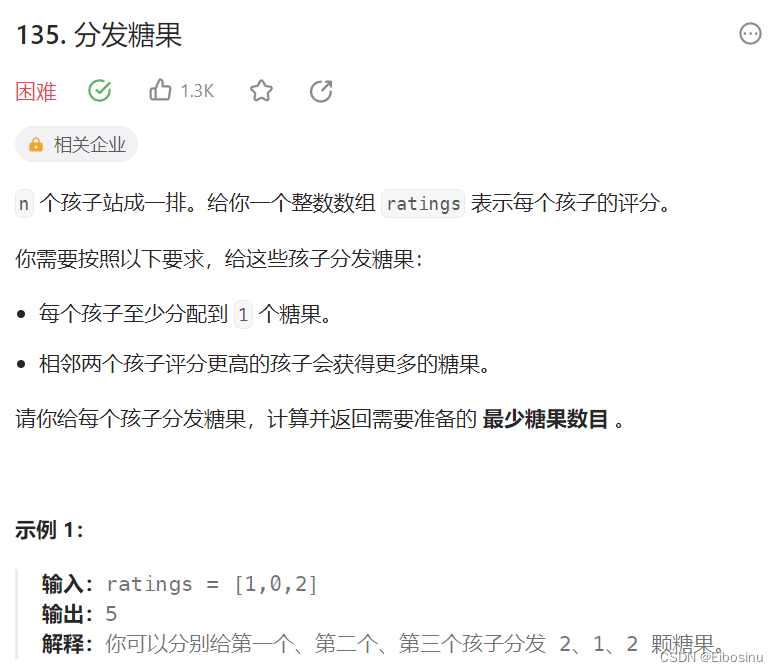
LeetCode刷题笔记【25】:贪心算法专题-3(K次取反后最大化的数组和、加油站、分发糖果)
文章目录 前置知识1005.K次取反后最大化的数组和题目描述分情况讨论贪心算法 134. 加油站题目描述暴力解法贪心算法 135. 分发糖果题目描述暴力解法贪心算法 总结 前置知识 参考前文 参考文章: LeetCode刷题笔记【23】:贪心算法专题-1(分发饼…...

java基础面试题 第四天
一、java基础面试题 第四天 1. String 为什么不可变? **不可变对象:**不可变对象在java中就是被final修饰的类就称为不可变对象,具体含义是,不可变对象一但被赋值以后,他的引用地址就不能被修改(它的属性…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
