机器学习——K最近邻算法(KNN)
机器学习——K最近邻算法(KNN)
文章目录
- 前言
- 一、原理
- 二、距离度量方法
- 2.1. 欧氏距离
- 2.2. 曼哈顿距离
- 2.3. 闵可夫斯基距离
- 2.4. 余弦相似度
- 2.5. 切比雪夫距离
- 2.6. 马哈拉诺比斯距离
- 2.7. 汉明距离
- 三、在MD编辑器中输入数学公式(额外)
- 四、代码实现
- 2.1. 用KNN算法进行分类
- 2.2. 用KNN算法进行回归
- 五、模型的保存和加载
- 总结
前言
在传统机器学习中,KNN算法是一种基于实例的学习算法,能解决分类和回归问题,而本文将介绍一下KNN即K最近邻算法。
一、原理
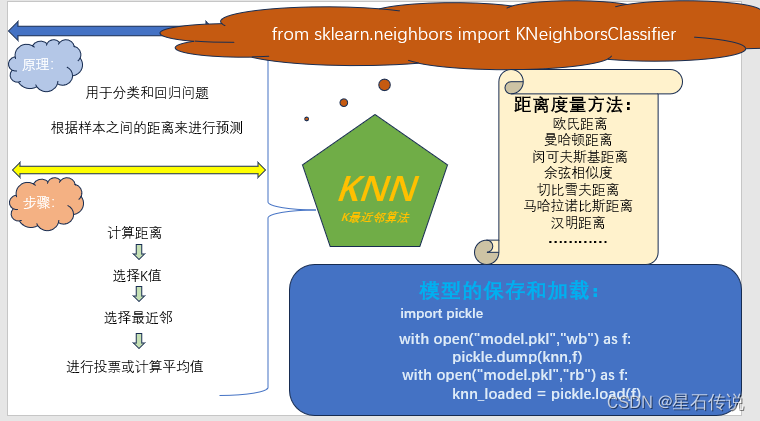
K最近邻(KNN)算法是一种基于实例的学习算法,用于分类和回归问题。它的原理是根据样本之间的距离来进行预测。
核心思想是通过找到与待分类样本最相似的K个训练样本,来确定待分类样本的类别或者预测其数值。
假设存在一个样本数据集(训练集),并且样本集中每个数据都存在标签(即知道样本集中数据的分类情况)
KNN算法的步骤如下:
-
计算距离:对于给定的未知样本(没有标签值的测试集),计算它与训练集中每个样本的距离。常用的距离度量方法有欧氏距离、曼哈顿距离等。
-
选择K值:选择一个合适的K值,即要考虑的最近邻的数量。
-
选择最近邻:从训练集中选择K个距离最近的样本。
-
进行投票或计算平均值:对于分类问题,根据最近邻的标签进行投票,选取票数最多的标签作为预测结果。对于回归问题,根据最近邻的值计算平均值作为预测结果。
按我的理解其实就是将待分类的样本与训练集中的每个样本去计算距离,然后从训练集中选择K个与待分类样本最靠近的几个样本,然后再根据选取得最靠近的几个样本得标签值进行投票来分类。
对于回归问题,则统计K个最近邻样本的数值,然后通过平均或加权平均的方式计算出待分类样本的数值。
如图所示(可看出K值的选择对结果有很大的影响):
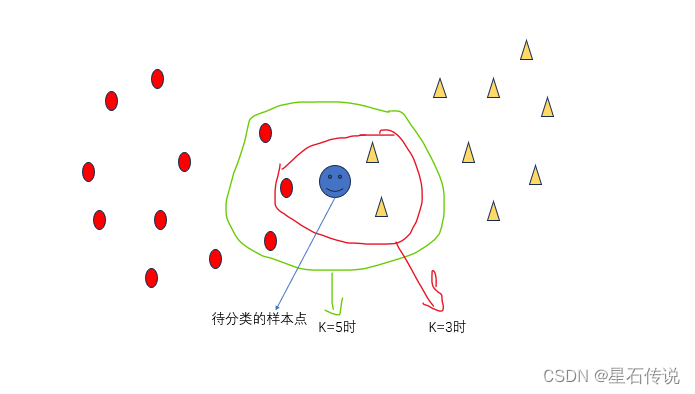
当K=3时,根据距离计算,待分类的样本点被划为黄色那一类;(因为2>1)
当K=5时, 根据距离计算,待分类的样本点被划为红色那一类;(因为3>2)
二、距离度量方法
参考文献
https://zhuanlan.zhihu.com/p/354289511
以下是一些常见的距离度量方法:
2.1. 欧氏距离
欧氏距离(Euclidean Distance):欧氏距离是最常见的距离度量方法,它是两个向量之间的直线距离。对于两个n维向量x和y,欧氏距离的计算公式为:
d ( x , y ) = ∑ i = 1 n ( x i − y i ) 2 d(x,y) = \sqrt{\sum_{i=1}^{n}(x_{i}-y_{i})^{2}} d(x,y)=i=1∑n(xi−yi)2
其中,xi和yi分别表示向量x和y的第i个元素。
例如当n = 2 时,这就是中学学的二维平面中两点之间距离公式的计算了。
2.2. 曼哈顿距离
曼哈顿距离(Manhattan Distance):曼哈顿距离是两个向量之间的城市街区距离,也称为L1距离。对于两个n维向量x和y,曼哈顿距离的计算公式为:
d ( x , y ) = ∑ i = 1 n ∣ x i − y i ∣ d(x,y) = \sum_{i=1}^{n} |x_{i} -y_{i}| d(x,y)=i=1∑n∣xi−yi∣
2.3. 闵可夫斯基距离
闵可夫斯基距离(Minkowski Distance):闵可夫斯基距离是欧氏距离和曼哈顿距离的一般化形式,它可以根据参数p的不同取值变化为不同的距离度量方法。对于两个n维向量x和y,闵可夫斯基距离的计算公式为:
d ( x , y ) = ∑ i = 1 n ∣ x i − y i ∣ p p d(x,y) = \sqrt[p]{\sum_{i=1}^{n}|x_{i}-y_{i}|^{p}} d(x,y)=pi=1∑n∣xi−yi∣p
其中,xi和yi分别表示向量x和y的第i个元素,p为参数,当p=2时,闵可夫斯基距离等价于欧氏距离;当p=1时,闵可夫斯基距离等价于曼哈顿距离。
2.4. 余弦相似度
余弦相似度(Cosine Similarity):余弦相似度是衡量两个向量方向相似程度的度量方法,它计算两个向量之间的夹角余弦值。对于两个n维向量x和y,余弦相似度的计算公式为:
c o s ( θ ) = ∑ i = 1 n ( x i ∗ y i ) ∑ i = 1 n ( x i ) 2 ∗ ∑ i = 1 n ( y i ) 2 cos(\theta ) = \frac{\sum_{i=1}^{n}(x_{i} * y_{i})}{\sqrt{\sum_{i=1}^{n}(x_{i})^{2}}*\sqrt{\sum_{i=1}^{n}(y_{i})^{2}}} cos(θ)=∑i=1n(xi)2∗∑i=1n(yi)2∑i=1n(xi∗yi)
2.5. 切比雪夫距离
切比雪夫距离(Chebyshev Distance):切比雪夫距离是两个向量之间的最大绝对差距。对于两个n维向量x和y,切比雪夫距离的计算公式为:
d ( x , y ) = m a x i ( ∣ p i − q i ∣ ) d(x,y) = \underset{i}{max}(|p_{i} -q_{i}|) d(x,y)=imax(∣pi−qi∣)
2.6. 马哈拉诺比斯距离
马哈拉诺比斯距离(Mahalanobis Distance):马哈拉诺比斯距离是一种考虑特征之间相关性的距离度量方法。它首先通过计算协方差矩阵来衡量特征之间的相关性,然后计算两个向量在经过协方差矩阵变换后的空间中的欧氏距离。对于两个n维向量x和y,马哈拉诺比斯距离的计算公式为:
d = ( x ⃗ − y ⃗ ) T S − 1 ( x ⃗ − y ⃗ ) d = \sqrt{(\vec{x}-\vec{y})^{T}S^{-1}(\vec{x}-\vec{y})} d=(x−y)TS−1(x−y)
其中,x和y分别表示向量x和y,S为x和y的协方差矩阵。
2.7. 汉明距离
汉明距离(Hamming Distance):汉明距离是用于比较两个等长字符串之间的差异的度量方法。对于两个等长字符串x和y,汉明距离的计算公式为:
d = 1 N ∑ i = 1 n 1 x i ≠ y i d = \frac{1}{N}\sum_{i=1}^{n}1_{x_{i}\neq y_{i}} d=N1i=1∑n1xi=yi
三、在MD编辑器中输入数学公式(额外)
在使用markdown文本编辑器时,对于数学公式的书写一般是使用到LaTeX这个排版系统,基于latex语法构建数学公式。
这对我这种刚开始接触的初学者是不友好的(在这之前还要学习LateX语法…)。
$$
$$
在这之间填入数学公式对应的LaTeX语法,就能获得对应的数学公式
对应的LaTeX语法可以从另一个编辑器——富文本编辑器 中获得:
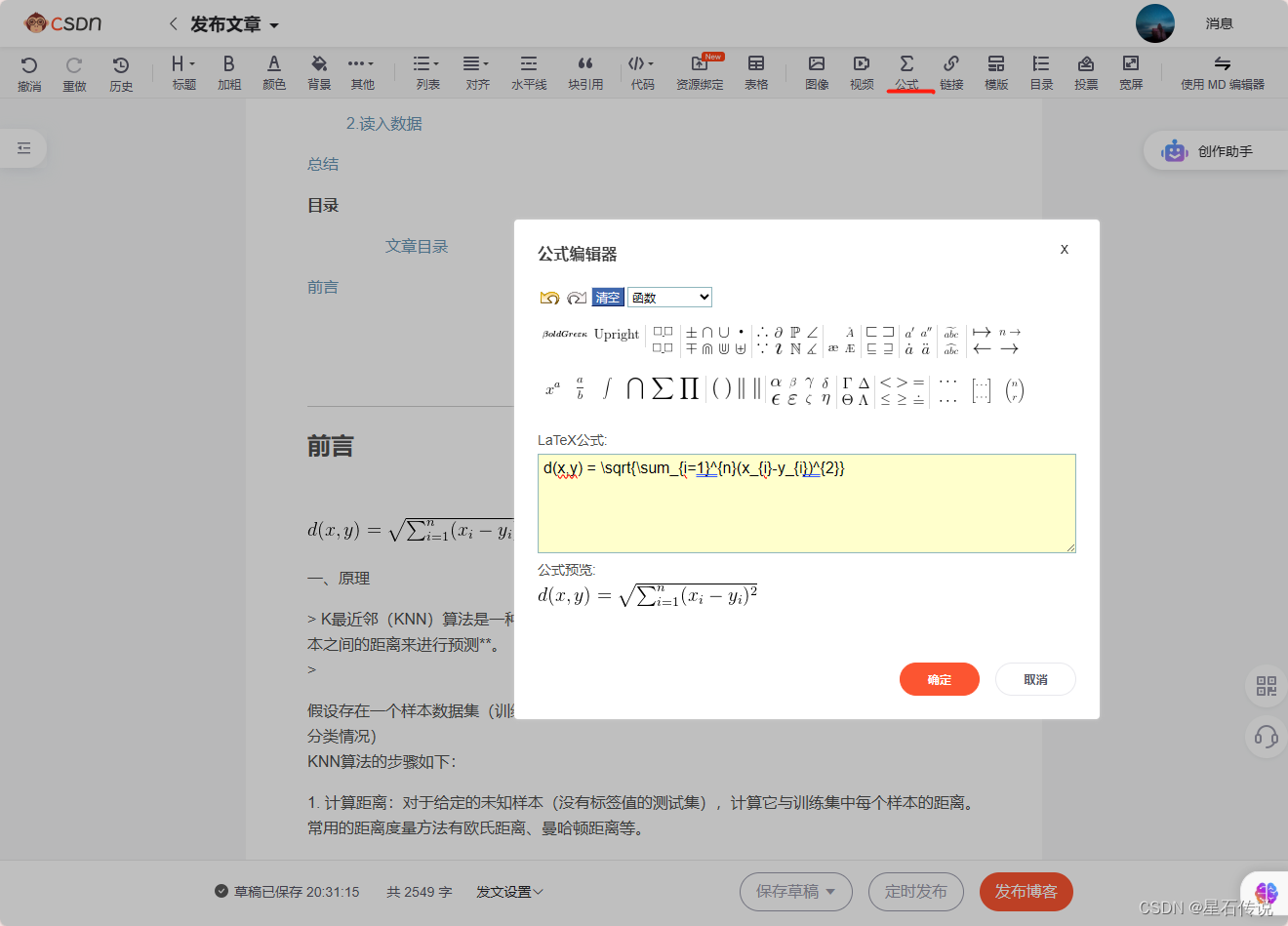
将LaTeX公式复制过来,d(x,y) = \sqrt{\sum_{i=1}{n}(x_{i}-y_{i}){2}}
$$
$$
放于这两个之间,可以得到对应公式:
d ( x , y ) = ∑ i = 1 n ( x i − y i ) 2 d(x,y) = \sqrt{\sum_{i=1}^{n}(x_{i}-y_{i})^{2}} d(x,y)=i=1∑n(xi−yi)2
嗯…,其实我也不太清楚为何我的Mardown编辑器中没有像富文本编辑器中那样的公式编辑器,(或许是要下载插件吗?),不用管这么多,能用就行。
四、代码实现
2.1. 用KNN算法进行分类
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=42)# 创建KNN分类器
knn = KNeighborsClassifier(n_neighbors=3)
#metric= "minkowski",距离度量默认是闵可夫斯基距离# 拟合模型
knn.fit(X_train, y_train)# 预测
y_pred = knn.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
Accuracy: 0.98333333333333332.2. 用KNN算法进行回归
from sklearn.neighbors import KNeighborsRegressor
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error# 加载数据集
boston = load_boston()
X = boston.data
y = boston.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建KNN回归器
knn = KNeighborsRegressor(n_neighbors=3)
# 拟合模型
knn.fit(X_train, y_train)
# 预测
y_pred = knn.predict(X_test)# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print("MSE:", mse)
MSE: 21.65955337690632#计算R方值
print(knn.score(X_test,y_test))
0.7046442656646525#绘图展示
import matplotlib.pyplot as plt
plt.style.use("ggplot")
plt.scatter(y_test,y_pred)
plt.plot([min(y_test),max(y_test)],[min(y_pred),max(y_pred)],"k--",color = "green", lw = 2,)
plt.xlabel("y_test")
plt.ylabel("y_pred")
plt.show()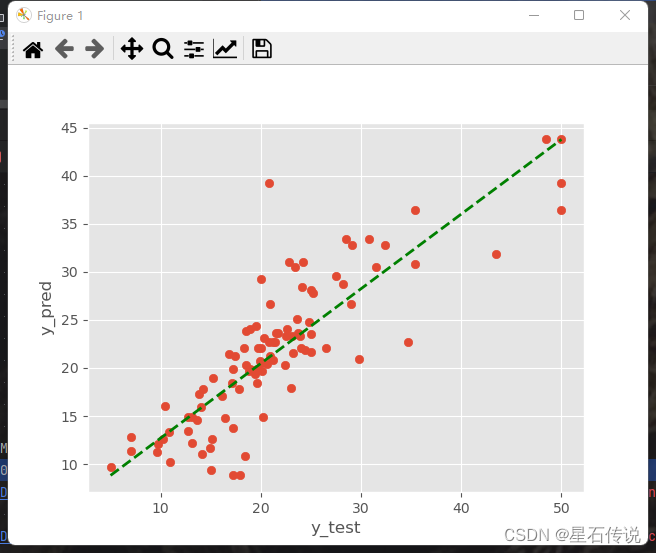
均方误差:
M S E = ∑ i = 1 n ( y t − y p ) 2 n MSE = \frac{\sum_{i=1}^{n}(y_t - y_p)^{2}}{n} MSE=n∑i=1n(yt−yp)2
再用线性回归试一下:
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
coefficients = model.coef_
intercept = model.intercept_# 构建回归公式
equation = f"y = {intercept} + {coefficients[0]}*x1 + {coefficients[1]}*x2 + ..."# 计算R^2值
r2_score = model.score(X_test, y_test)
print("R^2值:", r2_score)
R^2值: 0.6687594935356289
这些模型都是十分简单的模型,还未经过参数的调优和算法的优化。
五、模型的保存和加载
#模型的保存和加载
import pickle
with open("model.pkl","wb") as f:pickle.dump(knn,f)
with open("model.pkl","rb") as f:knn_loaded = pickle.load(f)print(knn_loaded.score(X_test,y_test))
0.7046442656646525
总结
本文从KNN算法的原理:(根据样本之间的距离来预测)出发,介绍了一些常见的距离度量方法,另外也介绍了一下在Markdown编辑器中输入数学公式,最后就是KNN算法在python中的分类和回归代码的实现。最后的最后就是模型的保存和加载。
道可道,非常道;名可名,非常名。
–2023-9-10 筑基篇
相关文章:

机器学习——K最近邻算法(KNN)
机器学习——K最近邻算法(KNN) 文章目录 前言一、原理二、距离度量方法2.1. 欧氏距离2.2. 曼哈顿距离2.3. 闵可夫斯基距离2.4. 余弦相似度2.5. 切比雪夫距离2.6. 马哈拉诺比斯距离2.7. 汉明距离 三、在MD编辑器中输入数学公式(额外࿰…...
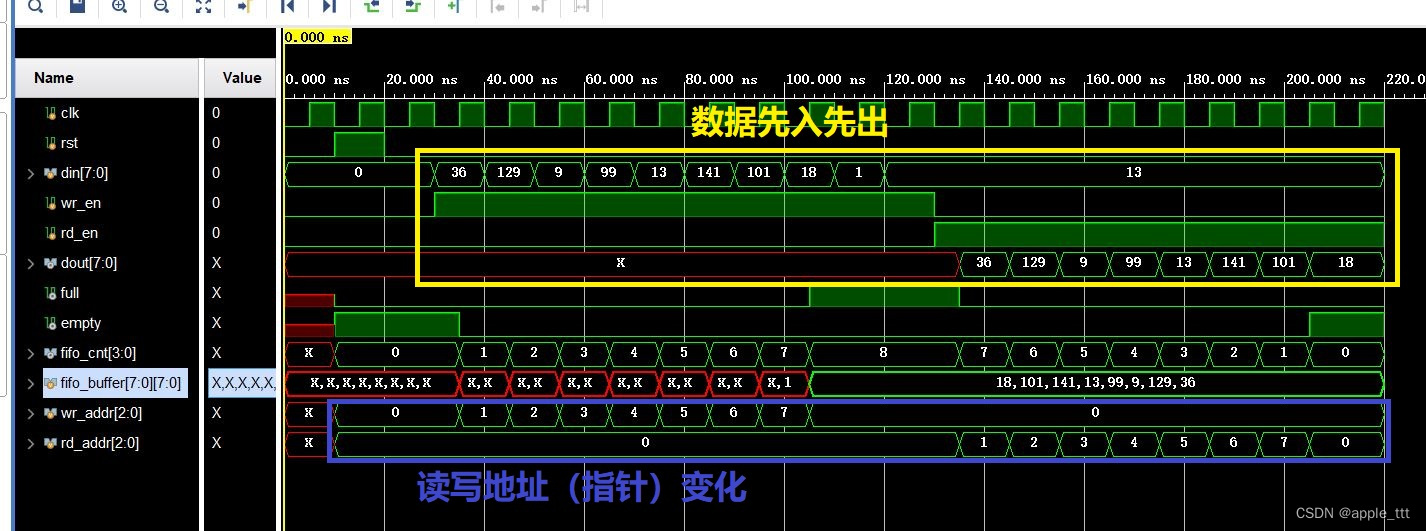
同步FIFO的verilog实现(1)——计数法
一、FIFO概述 1、FIFO的定义 FIFO是英文First-In-First-Out的缩写,是一种先入先出的数据缓冲器,与一般的存储器的区别在于没有地址线, 使用起来简单,缺点是只能顺序读写数据,其数据地址由内部读写指针自动加1完成&…...

python正则表达式笔记1
最近工作中经常用到正则表达式处理数据,慢慢发现了正则表达式的强大功能,尤其在数据处理工作中,记录下来分享给大家。 一、 正则表达式语法介绍 正则表达式(或 RE)指定了一组与之匹配的字符串;模块内的函…...

YOLO目标检测——口罩规范佩戴数据集+已标注xml和txt格式标签下载分享
实际项目应用:目标检测口罩佩戴检测数据集的应用场景涵盖了公共场所监控、疫情防控管理、安全管理与控制以及人员统计和分析等领域。这些应用场景可以帮助相关部门和机构更好地管理口罩佩戴情况,提高公共卫生和安全水平,保障人们的健康和安全…...

Android 13 - Media框架(9)- NuPlayer::Decoder
这一节我们将了解 NuPlayer::Decoder,学习如何将 MediaCodec wrap 成一个强大的 Decoder。这一节会提前讲到 MediaCodec 相关的内容,如果看不大懂可以先跳过此篇。原先觉得 Decoder 部分简单,越读越发现自己的无知,Android 源码真…...

23.09.5 《CLR via C#》 笔记5
第六章 类型和成员基础 类型可以定义0或多个以下成员:常量、字段、实例构造器、类型构造器、方法、操作符重载、转换操作符、属性、事件、类型类型的可见性分为public和internal(默认)C#中,成员的可访问性分为private、protected、internal、protected …...

laravel部署api项目遇到问题总结
laravel线上部署问题 一、Ubuntu远程Mysql 61“Connection refused”二、Ubuntu更新php8三、线上部署Permission denied3.1、部署完之后访问域名出现报错:3.2、The /bootstrap/cache directory must be present and writable. 四、图片访问404五、git部署线上文件 一…...

lintcode 1646 · 合法组合【字符串DFS, vip 中等 好题】
题目 https://www.lintcode.com/problem/1646 给一个单词s,和一个字符串集合str。这个单词每次去掉一个字母,直到剩下最后一个字母。求验证是否存在一种删除的顺序,这个顺序下所有的单词都在str中。例如单词是’abc’,字符串集合是{‘a’,’…...
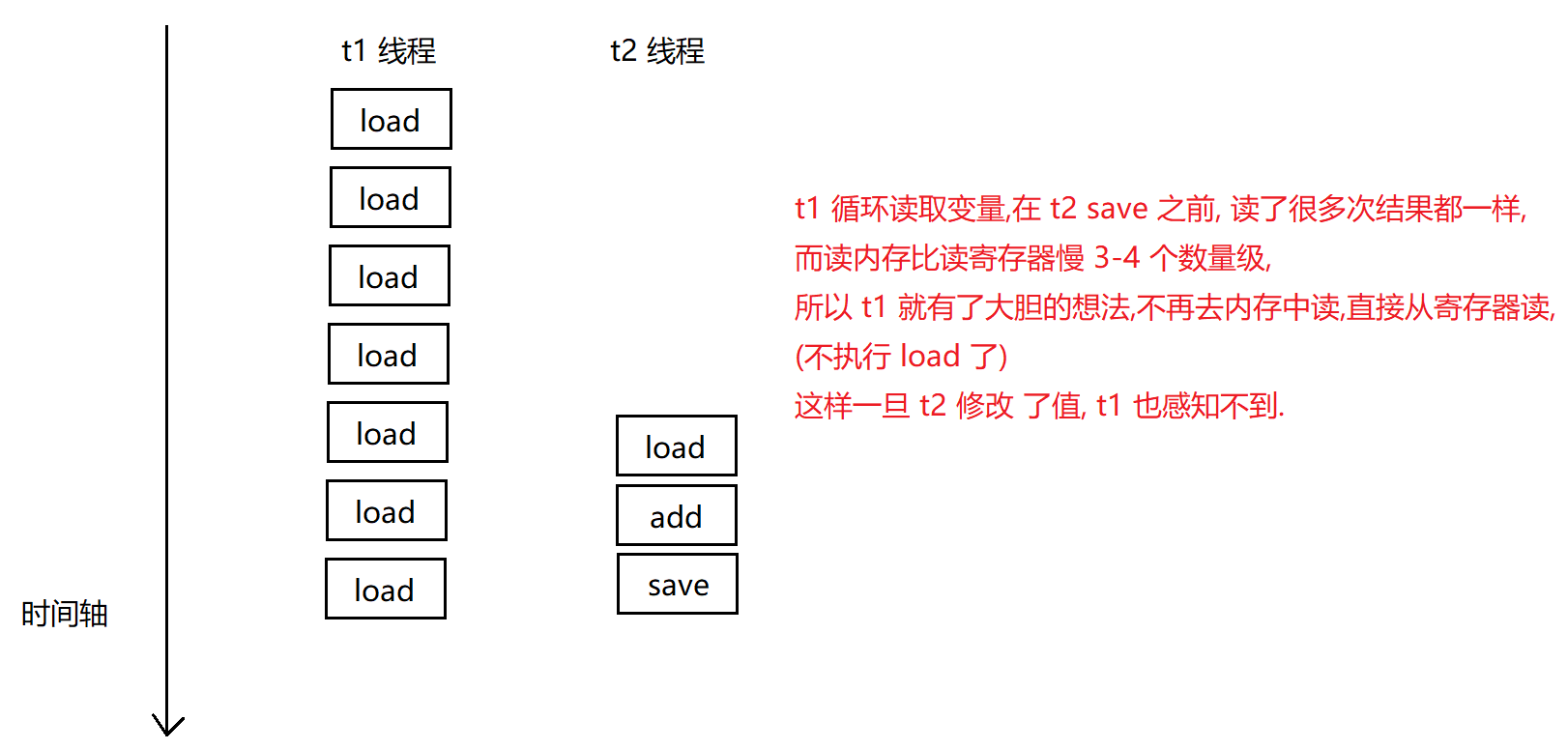
【多线程】线程安全 问题
线程安全 问题 一. 线程不安全的典型例子二. 线程安全的概念三. 线程不安全的原因1. 线程调度的抢占式执行2. 修改共享数据3. 原子性4. 内存可见性5. 指令重排序 一. 线程不安全的典型例子 class ThreadDemo {static class Counter {public int count 0;void increase() {cou…...

【用unity实现100个游戏之11】复刻经典消消乐游戏
文章目录 前言开始项目开始一、方块网格生成二、方块交换三、添加交换的动画效果四、水平消除检测五、垂直消除检测六、完善删除功能七、效果优化(移动方块后再进行消除检测)八、方块下落十、方块填充十一、后续 源码参考完结 前言 欢迎来到经典消消乐游…...
若依cloud 修改包名等
一、项目的项目名。 先改pom 然后在重命名文件 1、 修改主pom.xml <artifactId>ruoyi-api</artifactId> 缓存 <artifactId>zxf-api</artifactId> <groupId>com.ruoyi</groupId> <groupId>com.zhixiaofeng</groupId> 2、…...

健康系统练习
健康系统 项目建构: 前后端分离,前端vue3,后端Java,springboot做跨域处理,前端将在vscode中 的tomcat下部署,后端将在ideal中集成的tomcat中部署 创建项目工程在ideal中直接选用springi…创建,…...
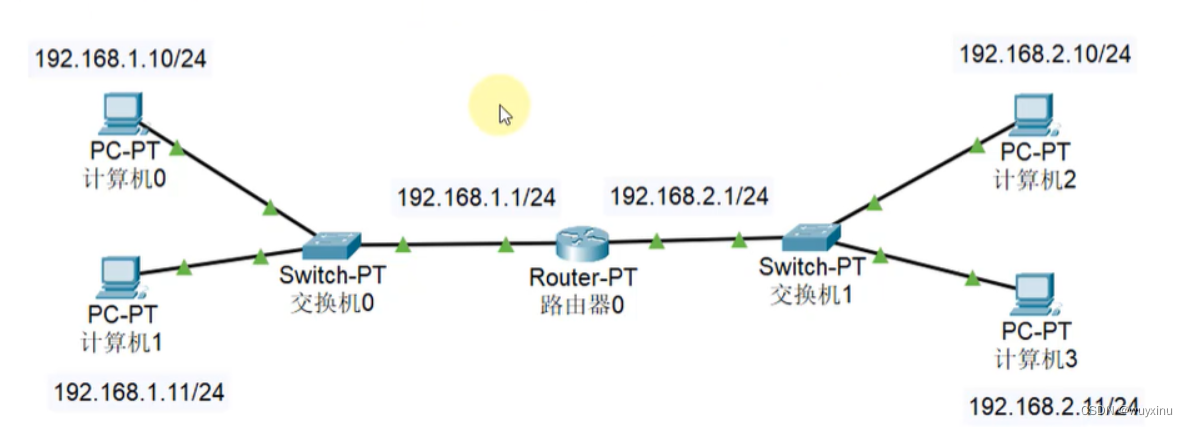
网络协议从入门到底层原理学习(一)—— 简介及基本概念
文章目录 网络协议从入门到底层原理学习(一)—— 简介及基本概念一、简介1、网络协议的定义2、网络协议组成要素3、广泛的网络协议类型网络通信协议网络安全协议网络管理协议 4、网络协议模型对比图 二、基本概念1、网络互连模型2、计算机之间的通信基础…...
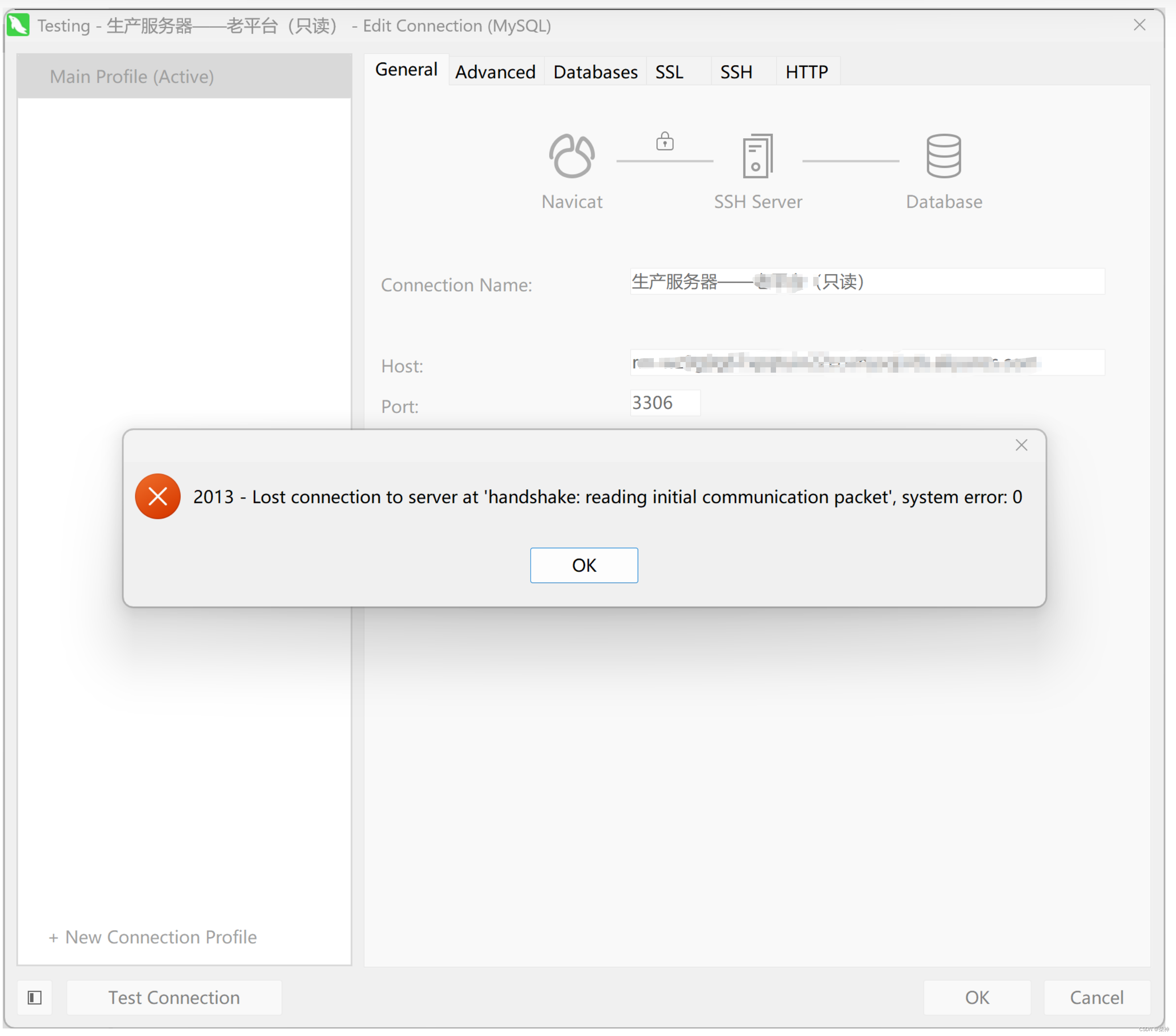
centos密码过期导致navicat无法通过SSH登录阿里云RDS问题
具体错误提示:2013 - Lost connection to server at "hand hake: reading initial communication packet, system error: 0 解决办法:更新SSH服务器密码...
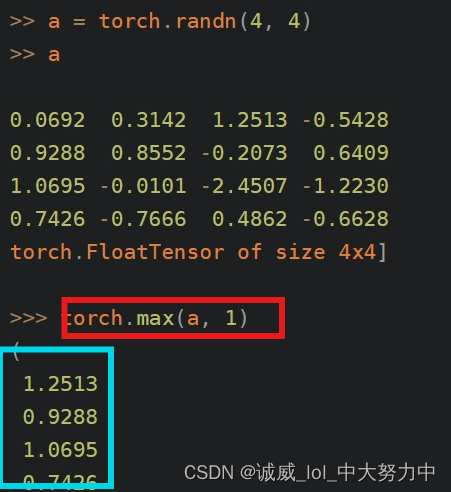
对于pytorch和对应pytorch网站的探索
一、关于网站上面的那个教程: 适合PyTorch小白的官网教程:Learning PyTorch With Examples - 知乎 (zhihu.com) 这个链接也是一样的, 总的来说,里面讲了这么一件事: 如果没有pytorch的分装好的nn.module用来继承的话,需要设计…...

和AI聊天:动态规划
动态规划 动态规划(Dynamic Programming,简称 DP)是一种常用于优化问题的算法。它解决的问题通常具有重叠子问题和最优子结构性质,可以通过将问题分解成相互依赖的子问题来求解整个问题的最优解。 动态规划算法主要分为以下几个步…...

微信小程序——使用插槽slot快捷开发
微信小程序的插槽(slot)是一种组件化的技术,用于在父组件中插入子组件的内容。通过插槽,可以将父组件中的一部分内容替换为子组件的内容,实现更灵活的组件复用和定制。 插槽的使用步骤如下: 在父组件的wx…...
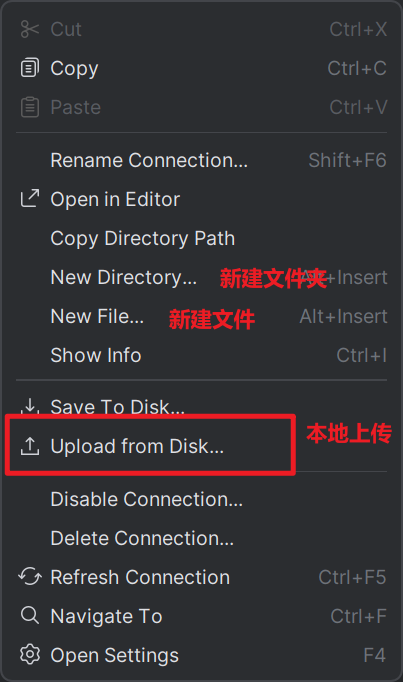
大数据技术之Hadoop:使用命令操作HDFS(四)
目录 一、创建文件夹 二、查看指定目录下的内容 三、上传文件到HDFS指定目录下 四、查看HDFS文件内容 五、下载HDFS文件 六、拷贝HDFS文件 七、HDFS数据移动操作 八、HDFS数据删除操作 九、HDFS的其他命令 十、hdfs web查看目录 十一、HDFS客户端工具 11.1 下载插件…...
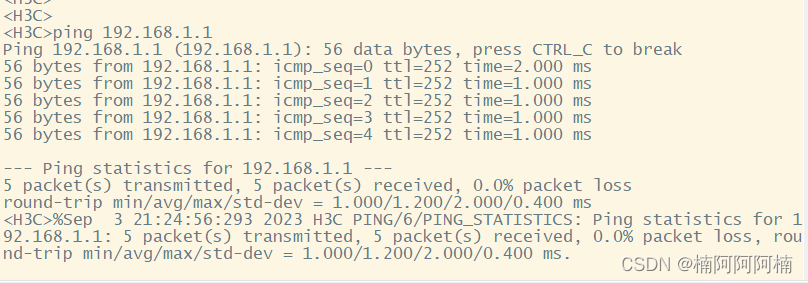
静态路由配置实验:构建多路由器网络拓扑实现不同业务网段互通
文章目录 一、实验背景与目的二、实验拓扑三、实验需求四、实验解法1. 配置 IP 地址2. 按照需求配置静态路由,实现连接 PC 的业务网段互通 摘要: 本实验旨在通过配置网络设备的IP地址和静态路由,实现不同业务网段之间的互通。通过构建一组具有…...

Python函数的概念以及定义方式
一. 前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 二. 什么是函数? 假设你现在是一个工人,如果你实现就准备好了工具,等你接收到任务的时候, 直接带上工…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
