和AI聊天:动态规划
动态规划
动态规划(Dynamic Programming,简称 DP)是一种常用于优化问题的算法。它解决的问题通常具有重叠子问题和最优子结构性质,可以通过将问题分解成相互依赖的子问题来求解整个问题的最优解。
动态规划算法主要分为以下几个步骤:
- 定义状态:将问题描述成一个状态模型,包括状态变量和状态转移方程。
- 初始化:将状态模型中的变量初始化为特定的值。
- 状态转移:根据状态转移方程,通过之前的状态计算当前状态的值。
- 计算最优解:通过计算得到最终的最优解。
动态规划算法的优点在于它可以避免重复计算,因此在处理复杂的问题时特别有用。然而,它的缺点在于,由于需要存储中间结果,它可能需要更多的空间来存储数据。
动态规划经典问题
以下是一些经典的动态规划问题:
- 最长公共子序列(LCS):给定两个字符串,求它们的最长公共子序列。
- 最长递增子序列(LIS):给定一个序列,求它的最长递增子序列。
- 背包问题:给定一个背包和一组物品,每个物品有重量和价值,求在不超过背包容量的情况下,能够获得的最大价值。
最长公共子序列(LCS)
最长公共子序列(LCS)问题是求解两个序列的最长公共子序列,即两个序列中都出现的最长的子序列。下面介绍一种常见的基于动态规划算法的求解方法:
令 m 和 n 分别为两个序列的长度,令 c[i][j] 表示第一个序列前 i 个元素和第二个序列前 j 个元素的 LCS 的长度,则有以下状态转移方程:
c[i][j] = c[i-1][j-1] + 1 (当第一个序列的第 i 个元素等于第二个序列的第 j 个元素时)
c[i][j] = max(c[i-1][j], c[i][j-1]) (当第一个序列的第 i 个元素不等于第二个序列的第 j 个元素时)
可以看出,当两个序列的当前元素相同时,LCS 长度加 1,否则 LCS 长度不变。因此,可以根据这个状态转移方程填充整个 c 数组。
最终,LCS 的长度即为 c[m][n],而具体的 LCS 可以通过反向追溯 c 数组得到。具体地,从 c[m][n] 开始,如果 c[i][j] 等于 c[i-1][j-1] + 1,则说明第一个序列中第 i 个元素和第二个序列中第 j 个元素都是 LCS 的元素之一,将它们加入 LCS 中;否则,根据 c[i][j] 是否等于 c[i-1][j] 或 c[i][j-1] 确定向左或向上移动。
这个算法的时间和空间复杂度均为 O(mn)。
以下是基于动态规划算法的最长公共子序列(LCS)问题的 C++ 代码实现:
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;int lcs(string s1, string s2) {int m = s1.length(), n = s2.length();int c[m+1][n+1];for (int i = 0; i <= m; i++)c[i][0] = 0;for (int i = 0; i <= n; i++)c[0][i] = 0;for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (s1[i-1] == s2[j-1])c[i][j] = c[i-1][j-1] + 1;elsec[i][j] = max(c[i-1][j], c[i][j-1]);}}return c[m][n];
}int main() {string s1 = "AGGTAB";string s2 = "GXTXAYB";cout << "LCS length: " << lcs(s1, s2) << endl;return 0;
}
运行结果为:
LCS length: 4
说明 “GTAB” 是两个序列的最长公共子序列。
最长递增子序列(LIS)
最长递增子序列(Longest Increasing Subsequence,LIS)问题是一个经典的动态规划问题。下面是具体的解法及C++代码实现。
一、解法
设dp[i]为以第i个元素为结尾的最长递增子序列的长度。dp[i]的值为前i-1个数中,所有比第i个数小的数的dp值加1的最大值。
以一个序列 { 5,3,4,8,6,7 }为例:
- dp[1] = 1;(序列:5)
- dp[2] = 1;(序列:3)
- dp[3] = 2;(序列:3,4)
- dp[4] = 3;(序列:3,4,8)
- dp[5] = 3;(序列:3,4,6)
- dp[6] = 4;(序列:3,4,6,7)
二、C++代码
#include <iostream>
#include <vector>
using namespace std;int lengthOfLIS(vector<int>& nums) {if (nums.empty()) return 0;int n = nums.size();vector<int> dp(n, 1); // 其中dp[i]表示以i结尾的最长递增子序列的长度,初始值都为1int res = 1;for (int i = 1; i < n; i++) { // 遍历到ifor (int j = 0; j < i; j++) { // 遍历到i之前的每个数if (nums[j] < nums[i]) {dp[i] = max(dp[i], dp[j]+1); // 更新最长递增子序列的长度}}res = max(res, dp[i]); // 更新最长递增子序列的长度的最大值}return res;
}int main() {vector<int> nums = {5, 3, 4, 8, 6, 7};cout << lengthOfLIS(nums) << endl; // 输出4return 0;
}
上述代码中使用了vector容器,可以方便的实现动态数组。
背包问题
一、01背包问题
给定n个物品和一个容量为W的背包,物品i的重量为wt[i],价值为val[i]。现在要求选若干件物品放入背包,使得放入的物品总重量不超过W,且价值最大。
01背包问题需要使用动态规划求解。设dp[i][j]表示前i个物品中,在总重量不超过j的情况下的最大价值。则有以下状态转移方程:
-
如果当前选的物品重量大于当前背包总重量,则不能选这个物品:dp[i][j] = dp[i-1][j]
-
否则,可以选或不选这个物品,取决于是否可以使总价值更大:
a. 选这个物品,总重量为j,则总价值为dp[i-1][j-wt[i]]+val[i]
b. 不选这个物品,则总价值为dp[i-1][j]
最终取dp[n][W]即为所求答案。
二、完全背包问题
完全背包问题和01背包问题的区别在于,每个物品可以选择无限次。设dp[i][j]表示前i个物品中,在总重量不超过j的情况下的最大价值。则有以下状态转移方程:
-
如果当前选的物品重量大于当前背包总重量,则不能选这个物品:dp[i][j] = dp[i-1][j]
-
否则,可以选或不选这个物品,取决于是否可以使总价值更大:
a. 选这个物品,总重量为j,则总价值为dp[i][j-wt[i]]+val[i]
b. 不选这个物品,则总价值为dp[i-1][j]
最终取dp[n][W]即为所求答案。
三、多重背包问题
多重背包问题和01背包问题的区别在于,每个物品的数量有限制。设dp[i][j]表示前i个物品中,在总重量不超过j的情况下的最大价值。则有以下状态转移方程:
-
如果当前选的物品重量大于当前背包总重量,则不能选这个物品:dp[i][j] = dp[i-1][j]
-
否则,可以选或不选这个物品,取决于是否可以使总价值更大:
a. 选这个物品,总重量为j,则总价值为dp[i][j-wt[i]]+val[i]
b. 不选这个物品,则总价值为dp[i-1][j]
需要注意的是,在更新dp[i][j]的时候,需要使用max函数比较选或不选这个物品的价值。同时,如果每个物品的数量有限制,还需要对物品数量进行处理。最终取dp[n][W]即为所求答案。
四、C++代码
01背包问题:
#include <iostream>
#include <vector>
using namespace std;int knapsack01(int W, vector<int>& wt, vector<int>& val) {int n = wt.size();vector<vector<int>> dp(n+1, vector<int>(W+1, 0)); // 初始化为0for (int i = 1; i <= n; i++) {for (int j = 1; j <= W; j++) {if (wt[i-1] > j) { // 当前选的物品重量大于当前背包总重量,不能选这个物品dp[i][j] = dp[i-1][j];} else {dp[i][j] = max(dp[i-1][j], dp[i-1][j-wt[i-1]]+val[i-1]); // 取选或不选这个物品的最大价值}}}return dp[n][W];
}int main() {int W = 10;vector<int> wt = {2, 2, 6, 5, 4};vector<int> val = {6, 3, 5, 4, 6};cout << knapsack01(W, wt, val) << endl; // 输出15return 0;
}
完全背包问题:
#include <iostream>
#include <vector>
using namespace std;int knapsackCom(int W, vector<int>& wt, vector<int>& val) {int n = wt.size();vector<vector<int>> dp(n+1, vector<int>(W+1, 0)); // 初始化为0for (int i = 1; i <= n; i++) {for (int j = 1; j <= W; j++) {if (wt[i-1] > j) { // 当前选的物品重量大于当前背包总重量,不能选这个物品dp[i][j] = dp[i-1][j];} else {dp[i][j] = max(dp[i-1][j], dp[i][j-wt[i-1]]+val[i-1]); // 取选或不选这个物品的最大价值}}}return dp[n][W];
}int main() {int W = 10;vector<int> wt = {2, 2, 6, 5, 4};vector<int> val = {6, 3, 5, 4, 6};cout << knapsackCom(W, wt, val) << endl; // 输出24return 0;
}
多重背包问题:
#include <iostream>
#include <vector>
using namespace std;int knapsackMul(int W, vector<int>& wt, vector<int>& val, vector<int>& cnt) {int n = wt.size();vector<vector<int>> dp(n+1, vector<int>(W+1, 0)); // 初始化为0for (int i = 1; i <= n; i++) {for (int j = 1; j <= W; j++) {if (wt[i-1] > j) { // 当前选的物品重量大于当前背包总重量,不能选这个物品dp[i][j] = dp[i-1][j];} else {for (int k = 0; k <= cnt[i-1]; k++) { // 对物品数量进行处理if (k*wt[i-1] > j) break; // 超过容量,退出循环dp[i][j] = max(dp[i-1][j], dp[i-1][j-k*wt[i-1]]+k*val[i-1]); // 取选或不选这个物品的最大价值}}}}return dp[n][W];
}int main() {int W = 10;vector<int> wt = {2, 2, 6, 5, 4};vector<int> val = {6, 3, 5, 4, 6};vector<int> cnt = {2, 3, 1, 4, 3};cout << knapsackMul(W, wt, val, cnt) << endl; // 输出54return 0;
}
相关文章:

和AI聊天:动态规划
动态规划 动态规划(Dynamic Programming,简称 DP)是一种常用于优化问题的算法。它解决的问题通常具有重叠子问题和最优子结构性质,可以通过将问题分解成相互依赖的子问题来求解整个问题的最优解。 动态规划算法主要分为以下几个步…...

微信小程序——使用插槽slot快捷开发
微信小程序的插槽(slot)是一种组件化的技术,用于在父组件中插入子组件的内容。通过插槽,可以将父组件中的一部分内容替换为子组件的内容,实现更灵活的组件复用和定制。 插槽的使用步骤如下: 在父组件的wx…...
大数据技术之Hadoop:使用命令操作HDFS(四)
目录 一、创建文件夹 二、查看指定目录下的内容 三、上传文件到HDFS指定目录下 四、查看HDFS文件内容 五、下载HDFS文件 六、拷贝HDFS文件 七、HDFS数据移动操作 八、HDFS数据删除操作 九、HDFS的其他命令 十、hdfs web查看目录 十一、HDFS客户端工具 11.1 下载插件…...
静态路由配置实验:构建多路由器网络拓扑实现不同业务网段互通
文章目录 一、实验背景与目的二、实验拓扑三、实验需求四、实验解法1. 配置 IP 地址2. 按照需求配置静态路由,实现连接 PC 的业务网段互通 摘要: 本实验旨在通过配置网络设备的IP地址和静态路由,实现不同业务网段之间的互通。通过构建一组具有…...

Python函数的概念以及定义方式
一. 前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 二. 什么是函数? 假设你现在是一个工人,如果你实现就准备好了工具,等你接收到任务的时候, 直接带上工…...
【数学建模竞赛】超详细Matlab二维三维图形绘制
二维图像绘制 绘制曲线图 g 是表示绿色 b--o是表示蓝色/虚线/o标记 c*是表示蓝绿色(cyan)/*标记 ‘MakerIndices,1:5:length(y) 每五个点取点(设置标记密度) 特殊符号的输入 序号 需求 函数字符结构 示例 1 上角标 ^{ } title( $ a…...

2023国赛数学建模E题思路代码 黄河水沙监测数据分析
E题最大的难度是数据处理,可以做一个假设,假设一定时间内流量跟含沙量不变,那么我们可以对数据进行向下填充,把所有的数据进行合并之后可以对其进行展开特性分析,在研究调水调沙的实际效果时,可以先通过分析…...
窗口延时、侧输出流数据处理
一 、 AllowedLateness API 延时关闭窗口 AllowedLateness 方法需要基于 WindowedStream 调用。AllowedLateness 需要设置一个延时时间,注意这个时间决定了窗口真正关闭的时间,而且是加上WaterMark的时间,例如 WaterMark的延时时间为2s&…...

发送HTTP请求
HTTP请求是一种客户端向服务器发送请求的协议。它是基于TCP/IP协议的应用层协议,用于在Web浏览器和Web服务器之间传输数据。 HTTP请求由以下几个部分组成: 请求行:包含请求方法、请求的URL和HTTP协议的版本。常见的请求方法有GET、POST、PUT、…...

高等工程数学张韵华版第四章课后题答案
下面答案仅供参考! 章节目录 第4章 欧氏空间和二次型 4.1内积和欧氏空间 4.1.1内积的定义 4.1.2欧氏空间的性质 4.1.3 正交投影 4.1.4 施密特正交化 4.2 正交变换和对称变换 4.2.1 正交变换 4.2.2 正交矩阵 4.2.3 对称变换 4.2.4 对称矩阵 4.3 二…...
wpf C# 用USB虚拟串口最高速下载大文件 每包400万字节 平均0.7s/M,支持批量多设备同时下载。自动识别串口。源码示例可自由定制。
C# 用USB虚拟串口下载大文件 每包400万字节 平均0.7s/M。支持批量多设备同时下载。自动识别串口。可自由定制。 int 32位有符号整数 -2147483648~2147483647 但500万字节时 write时报端口IO异常。可能是驱动限制的。 之前用这个助手发文件,连续发送࿰…...

代码随想录二刷day20
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣654. 最大二叉树二、力扣617. 合并二叉树三、力扣700. 二叉搜索树中的搜索四、力扣98. 验证二叉搜索树 前言 一、力扣654. 最大二叉树 /*** Definitio…...

Yolov5如何训练自定义的数据集,以及使用GPU训练,涵盖报错解决
本文主要讲述了Yolov5如何训练自定义的数据集,以及使用GPU训练,涵盖报错解决,案例是检测图片中是否有救生圈。 最后的效果图大致如下: 效果图1效果图2 前言 系列文章 1、详细讲述Yolov5从下载、配置及如何使用GPU运行 2、…...
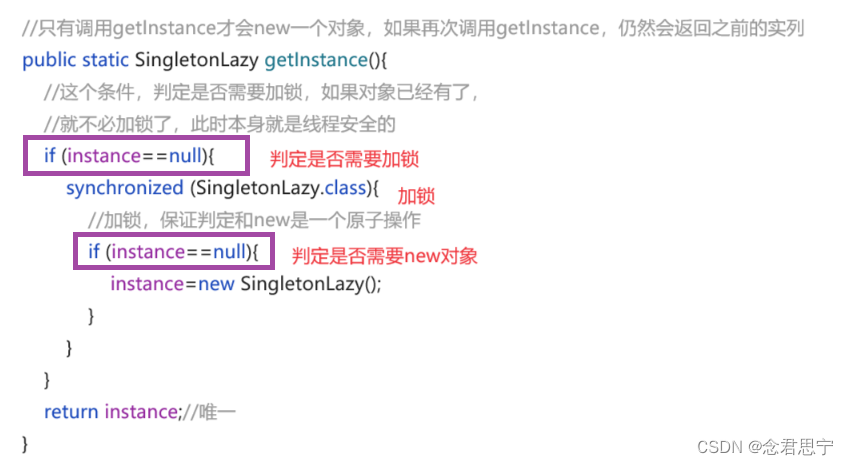
设计模式之单列模式
单列模式是一种经典的设计模式,在校招中最乐意考的设计模式之一~ 设计模式就是软件开发中的棋谱,大佬们针对一些常见的场景,总结出来的代码的编写套路,按照套路来写,不说你写的多好,至少不会太差~ 在校招中…...
linux内核模块编译方法详解
文章目录 前言一、静态加载法1.1 编写驱动程序1.2 将新功能配置在内核中1.3为新功能代码改写Makefile1.4 make menuconfig界面里将新功能对应的那项选择为<*> 二、动态加载法2.1 新功能源码与Linux内核源码在同一目录结构下2.2 新功能源码与Linux内核源码不在同一目录结构…...

简介shell的关联数组与普通数组
本文首先介绍shell的关联数组,然后介绍shell的普通数组,最后总结它们的共同语法。 shell的关联数组 定义一个关联数组,并打印它的key-value对 #!/bin/sh# 声明一个关联数组 declare -A HASH_MAP# 给关联数组赋值 HASH_MAP["Tom"…...

玩转Mysql系列 - 第17篇:存储过程自定义函数详解
这是Mysql系列第17篇。 环境:mysql5.7.25,cmd命令中进行演示。 代码中被[]包含的表示可选,|符号分开的表示可选其一。 需求背景介绍 线上程序有时候出现问题导致数据错误的时候,如果比较紧急,我们可以写一个存储来…...

自动驾驶:轨迹预测综述
自动驾驶:轨迹预测综述 轨迹预测的定义轨迹预测的分类基于物理的方法(Physics-based)基于机器学习的方法(Classic Machine Learning-based)基于深度学习的方法(Deep Learning-based)基于强化学习…...

【uniapp/uview】u-datetime-picker 选择器的过滤器用法
引入:要求日期选择的下拉框在分钟显示时,只显示 0 和 30 分钟; <u-datetime-picker :show"dateShow" :filter"timeFilter" confirm"selDateConfirm" cancel"dateCancel" v-model"value1&qu…...

如何使用Docker部署Nacos服务?Nacos Docker 快速部署指南: 一站式部署与配置教程
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
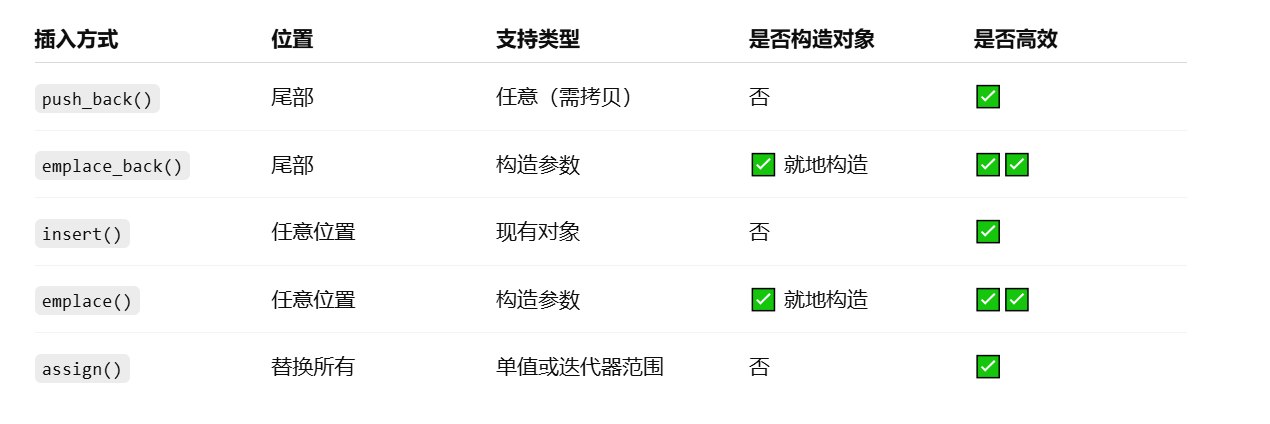
C++中vector类型的介绍和使用
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...
