【C++】封装map和set(红黑树实现)
前言:
前面,我们学习了set和map的用法,这两个容器可以完成查找,排序等操作,后来我们在学习过二叉搜索树的基础上又学习了两种特殊的二叉搜索树——AVL树和红黑树,他们俩可以是效率进一步提高,其实set和map的底层就是由红黑树封装而成的!
所以,本篇文章我们自己学习用红黑树封装set和map。用红黑树封装,特别是用同一棵红黑树实现封装有一定的难度,其中很多操作(比如复用)我们会第一次尝试,所以大家请跟紧作者的脚步来。
目录
(一)如何复用同一棵红黑树
(二)红黑树的改造流程(为封装做铺垫)
1、结点的定义
2、模拟实现结点的比较大小
3、改造后的红黑树
4、map和set迭代器的模拟实现
4.1模版参数的构成
4.2begin()和end()的模拟实现
4.3operator* 和 operator->模拟实现
4.4 operator++ 和 operator--模拟实现
4.5 operator== 和 operator!=模拟实现
4.6迭代器代码详解
(三)封装map和set
(一)如何复用同一棵红黑树
前提疑问:
在我们这所有的之前我们知道,map和set这两个容器都是用红黑树来实现的,那么就有了接下来的问题。
- map和set都是用的同一棵红黑树复用的吗
- 或者这两个容器各自使用一棵红黑树吗
其实在前言中我们就知道了,根据STL的设计理念和泛型编程的理念,我们不会冗余的写两课红黑树,而是用一棵红黑树实现复用的效果。
我们调用STL库中的原码来看:

我们发现:
- STL库中的原码也确实调用的同一棵红黑树
- 他们实现的都是key_value模型
我们设set中存放结点的值是K,map中存放的节点是pair<key,value>键值对:
- 对于set而言,底层红黑树的模版就是RBTree<K, K>
- 对于map而言,底层红黑树的模版就是RBTree<K, pair<K, V>>
这时我们就有了另一个疑问,两个模板参数的第一个Key,不能省略掉吗??
- 首先,答案肯定是不能的
- 那么原因又是什么呢?
因为map的这个类中,无论怎么省略都会有一个查找函数要单独用到Key

如果第一个Key删去了,那么map和set的查找函数就没法统一实现了,违背了我们一开始泛型编程的思想。
综上所述:
- map和set都是用了,Key_value模型
- set中的K是K,V也是K
- map中的K是K,V是pair<K,V>
- 并且模板参数中第一个K都不能省
(二)红黑树的改造流程(为封装做铺垫)
1、结点的定义
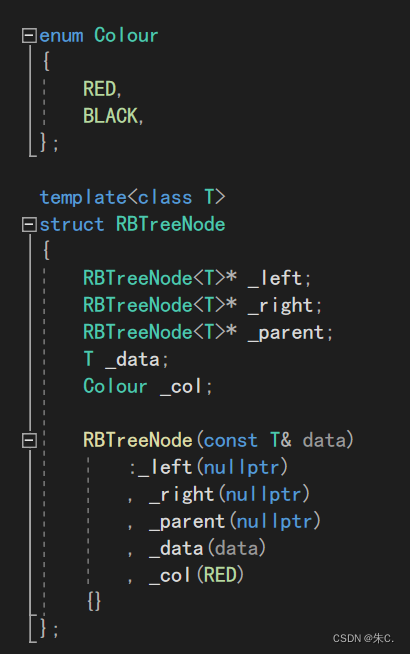
这里由于set和map存放的结点一个是Key一个是pair<Key,Value>,所以我们使用模版,把存放的结点泛化。
2、模拟实现结点的比较大小
- 上述提到,在模拟实现中,map和set我们复用同一棵红黑树的时候都是用的是Kye_value的结构
- 但是红黑树中的数据比较又是Key值的比较,而现在我们用的则是pair的比较
- 虽然编译上是可以通过但是真的就是我们所想要的吗?
pair的比较大小:

很显然这种比较规则不是我们所想要的,并且map和set想要取到用来比较的数据是不同的。
为了取到我们想要的数据,我们引入了仿函数:
- 根据map和set的需求不同
- 我们在红黑树中新引入了一个模板参数KeyOfT

引入KeyOfT模板参数后,我们想要不同方式的比较方法只需要在set和map的封装中给出属于他们自己的比较仿函数。
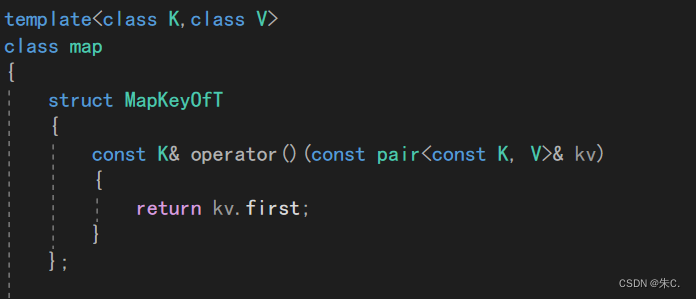
map中的仿函数:
set中的仿函数:
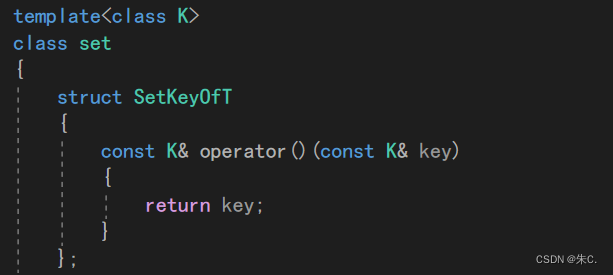
使用方法:
此时前面所说的仿函数的便利之处就体现出来了。
3、改造后的红黑树
具体代码:
//红黑树的实现
//KeyOfT --> 支持取出T对象中key的仿函数
template<class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
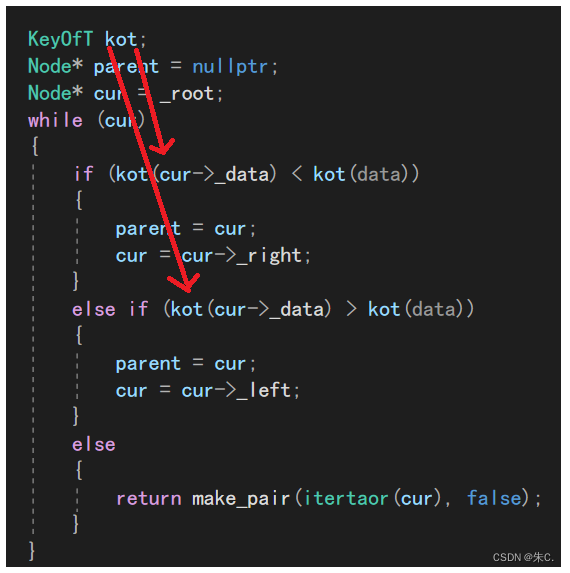
public:typedef __RBTreeIterator<T, T&, T*> iterator;typedef __RBTreeIterator<T, const T&, const T*> const_iterator;//构造 拷贝构造 赋值 和析构 跟搜索树实现方式是一样的//迭代器中序遍历,要找最左结点iterator Begin(){Node* subLeft = _root;while (subLeft && subLeft->_left){subLeft = subLeft->_left;}//树的迭代器用结点的指针就可以构造return iterator(subLeft);}iterator End(){return iterator(nullptr);}const_iterator Begin() const{Node* subLeft = _root;while (subLeft && subLeft->_left){subLeft = subLeft->_left;}//树的迭代器用结点的指针就可以构造return const_iterator(subLeft);}const_iterator End() const{return const_iterator(nullptr);}pair<iterator, bool> Insert(const T& data){//1、搜索树的规则插入//2、看是否违反平衡规则,如果违反就需要处理:旋转if (_root == nullptr){_root = new Node(data);_root->_col = BLACK; //根节点是黑色return make_pair(iterator(_root), true);}KeyOfT kot;Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(iterator(cur), false);}}//找到符合规则的位置之后再插入cur = new Node(data); Node* newnode = cur;cur->_col = RED;if (kot(parent->_data) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}//三叉链的链接 -- 链上父节点cur->_parent = parent;//存在连续红色结点while (parent && parent->_col == RED){//理论而言,祖父是一定存在的,父亲存在且是红不可能是根(根一定是黑的)Node* grandfather = parent->_parent;assert(grandfather);if (grandfather->_left == parent){Node* uncle = grandfather->_right;//情况一:(叔叔存在且为红)if (uncle && uncle->_col == RED){//祖父和叔叔变成黑色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上处理cur = grandfather;parent = cur->_parent;}//情况二:(叔叔不存在 or 叔叔存在且为黑)else{//单旋// g// p// cif (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}//双旋// g// p// celse{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}//无论父亲和叔叔是左是右都是一样的//grandfather->_right == parent;else{Node* uncle = grandfather->_left;//情况一:if (uncle && uncle->_col == RED){//祖父和叔叔变成黑色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上处理cur = grandfather;parent = cur->_parent;}else{//单旋// g// p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}//双旋// g// p// celse{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}//父亲为空就出循环,将根节点设置成黑色_root->_col = BLACK;return make_pair(iterator(newnode), true);}
}
插入(Insert)和寻找(Find)代码:
Node* Find(const K& key){Node* cur = _root;KeyOfT kot;while (cur){if (kot(cur->_data) < key){cur = cur->_right;}else if (kot(cur->_data) > key){cur = cur->_left;}else{return cur;}}return nullptr;}pair<itertaor, bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(itertaor(_root), true);}KeyOfT kot;Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(itertaor(cur), false);}}cur = new Node(data);Node* newnode = cur;if (kot(parent->_data) > kot(data)){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (grandfather->_left == parent){Node* uncle = grandfather->_right;// 情况1:u存在且为红,变色处理,并继续往上处理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 继续往上调整cur = grandfather;parent = cur->_parent;}else // 情况2+3:u不存在/u存在且为黑,旋转+变色{// g// p u// c if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;//parent->_col = RED;grandfather->_col = RED;}break;}}else // (grandfather->_right == parent){// g// u p// cNode* uncle = grandfather->_left;// 情况1:u存在且为红,变色处理,并继续往上处理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 继续往上调整cur = grandfather;parent = cur->_parent;}else // 情况2+3:u不存在/u存在且为黑,旋转+变色{// g// u p// cif (cur == parent->_right){RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(itertaor(newnode), true);;}4、map和set迭代器的模拟实现
上面改造后的红黑树中已经涉及到了迭代器,这里我们来模拟实现。
备注:
- T:数据
- Ref:引用
- Ptr:指针
- Sef:iterator本身
4.1模版参数的构成
要想实现同一棵红黑树的复用,模版参数的构成极为重要。
之前我们也遇到过相似的情况,我们这里的实现方法参看之前。
迭代器的实现中:
- 涉及到了*解引用操作,返回的是数据的引用;
- 涉及到了->指针操作,返回的是数据的地址;
- 涉及到++,--操作,返回的是操作后迭代器本身的位置。
但是以上的行为,我们都涉及结点,所以结点的数据类型也尤为重要!
综上,模版参数的构成如下图:
4.2begin()和end()的模拟实现

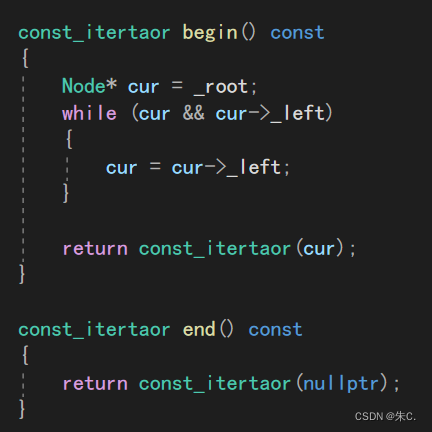
- 因为是二叉搜索树,为了更有顺序,所以我们采取的是中序遍历。
- 那么中序遍历Begin()就应该是最左结点
- 我们实现的版本中End()定义为空是(nullptr)
ps:
而库中的红黑树则是设计了一个哨兵位的头结点: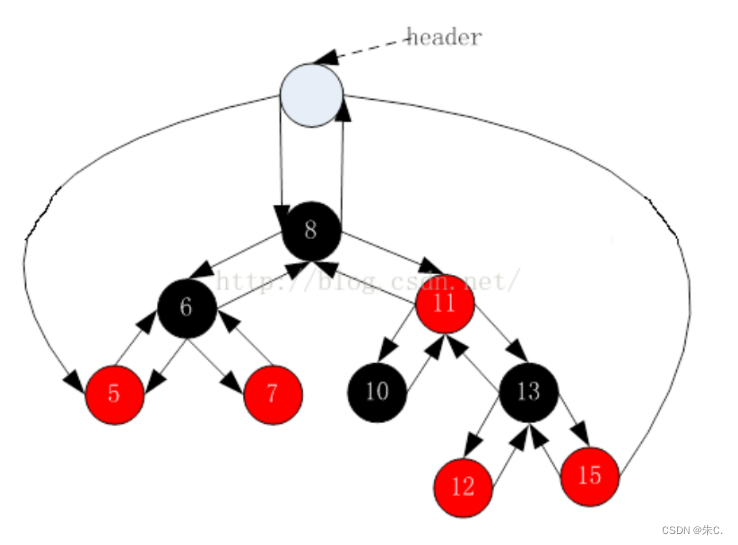
所以我们实现的只是简化版本。
4.3operator* 和 operator->模拟实现

就是正常的运用operator,但是operator->和list中讲的一样,返回的是地址的原因是为了连续访问(连续的operator->会优化成一个->)
4.4 operator++ 和 operator--模拟实现
这里迭代器的++和- - 需要分类一下,分别是:前置++,- - 、后置++,- -
前置++ :
因为我们是中序遍历,我们访问完自己之后,下一个该访问哪一个结点?
我们观察任何一棵二叉树都能看出,无非是下面两种情况:
分如下两种情况:(重点)
- 右子树为空:找孩子是父亲的左的那个祖先节点,否则继续往上走,直到空(nullptr)
- 右子树为非空:找右子树的最左节点
这一过程有点类似于递归思想,但是是非递归实现的
代码实现:

前置-- :
有了上面的思路,我们联想一下,现在需要看当前位置左子树是否是空。
前置- -就是倒着走,同样还是对当前位置分两种情况:(重点)
- 左子树为空:找孩子是父亲的右的那个祖先节点,否则继续往上走,直到空(nullptr)
- 左子树为非空:找左子树的最右节点

只要前置++理解了,那么前置- -完全就是前置++倒过来走一遍。
后置++、后置- - :
和之前实现容器的得带器一样,我们这里直接复用即可:

4.5 operator== 和 operator!=模拟实现
有了之前封装迭代器的经验,这两个的视线还是比较容易得:

4.6迭代器代码详解
template<class T, class Ref, class Ptr>
struct __RBTreeIterator
{typedef RBTreeNode<T> Node;Node* _node;typedef __RBTreeIterator<T, Ref, Ptr> Self;__RBTreeIterator(Node* node):_node(node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}Self& operator++(){if (_node->_right == nullptr){//找祖先里面,孩子是父亲左的那个Node* cur = _node;Node* parent = cur->_parent;while (parent && parent->_right == cur){cur = cur->_parent;parent = parent->_parent;}_node = parent;}else{//右子树的最左结点Node* subLeft = _node->_right;while (subLeft->_left){subLeft = subLeft->_left;}//左为空_node = subLeft;}return *this;}Self& operator--(){if (_node->_left == nullptr){//找祖先里面,孩子是父亲Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = cur->_parent;parent = parent->_parent;}_node = parent;}else{//左子树的最右结点Node* subRight = _node->_left;while (subRight->_right){subRight = subRight->_right;}_node = subRight;}return *this;}Self operator++(int){Self tmp(*this);++(*this);return tmp;}Self operator--(int){Self tmp(*this);--(*this);return tmp;}bool operator!=(const Self& s) const{return _node != s._node;}bool operator==(const Self& s) const{return _node == s._node;}
};
(三)封装map和set
有了上面的红黑树的改装,我们这里的对map和set的封装就显得很得心应手了。
封装主要是把map和set的基本操作封装在一个类中。
map的封装:
template<class K, class V>
class map
{//定义一个内部类struct MapKeyOfT{const K& operator()(const pair<K, V>& kv)//operator() 可以像函数一样去使用{return kv.first;}};public:typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::const_iterator const_iterator;iterator begin(){return _t.Begin();}iterator end(){return _t.End();}pair<iterator, bool> insert(const pair<K, V>& kv){return _t.Insert(kv);}V& operator[](const K& key){pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;}
private:RBTree<K, pair<K, V>, MapKeyOfT> _t;
};
这里map中的operator[ ]我们知道其原理之后,模拟实现就非常方便,直接调用插入函数,控制好参数和返回值即可。
对set的封装:
template<class K>
class set
{struct SetKeyOfT{const K& operator()(const K& key)//operator() 可以像函数一样去使用{return key;}};
public://加上typename告诉编译器这是个类型,类模板实例化了再去取typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;iterator begin() const{return _t.Begin();}iterator end() const{return _t.End();}pair<iterator, bool> insert(const K& key){//pair<typename RBTree<K, K, SetKeyOfT>::iterator, bool> ret = _t.Insert(key);auto ret = _t.Insert(key);return pair<iterator, bool>(iterator(ret.first._node), ret.second);}iterator find(const K& key){return _t.Find(key);}private:RBTree<K, K, SetKeyOfT> _t;
};
附详细代码:——》红黑树封装map和set
相关文章:

【C++】封装map和set(红黑树实现)
前言: 前面,我们学习了set和map的用法,这两个容器可以完成查找,排序等操作,后来我们在学习过二叉搜索树的基础上又学习了两种特殊的二叉搜索树——AVL树和红黑树,他们俩可以是效率进一步提高,其…...
【补】代码随想录算法训练营day38|动态规划 |509. 斐波那契数|70. 爬楼梯|746. 使用最小花费爬楼梯
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推…...
C语言sizeof()计算空间大小为8的问题
在练习数据结构过程中,定义指针p,并且申请了10个char类型空间,但在计算p所指空间大小时候,发现了一些奇怪的现象。 #include <stdio.h> #include <stdlib.h>int main(){char s[12];printf("the size of memory …...
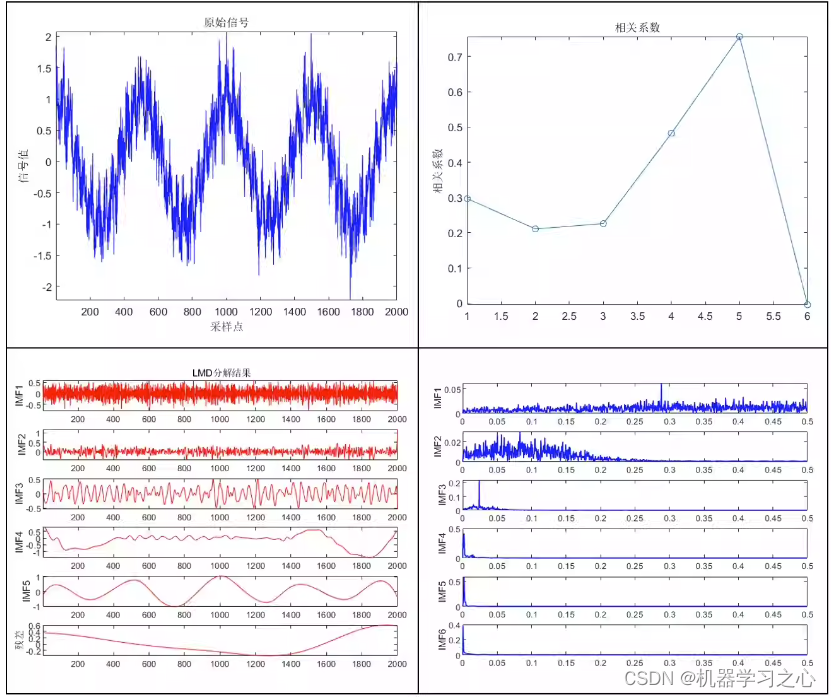
时序分解 | MATLAB实现基于LMD局部均值分解的信号分解分量可视化
时序分解 | MATLAB实现基于LMD局部均值分解的信号分解分量可视化 目录 时序分解 | MATLAB实现基于LMD局部均值分解的信号分解分量可视化效果一览基本介绍程序设计参考资料 效果一览 基本介绍 LMD局部均值分解 直接替换Excel即可运行包含频谱图相关系数图 Matlab语言 1.算法新颖…...

景区AR虚拟三维场景沉浸式体验成为新兴的营销手段
科技的迅速崛起正在改变我们的世界,旅游业也在这股浪潮中掀起了一场全新的变革。增强现实(AR)技术正成为旅行中的一股强大力量,通过增添趣味和交互性,为旅程注入了前所未有的活力。本文将带您深入了解AR如何为旅游带来全新的体验,…...
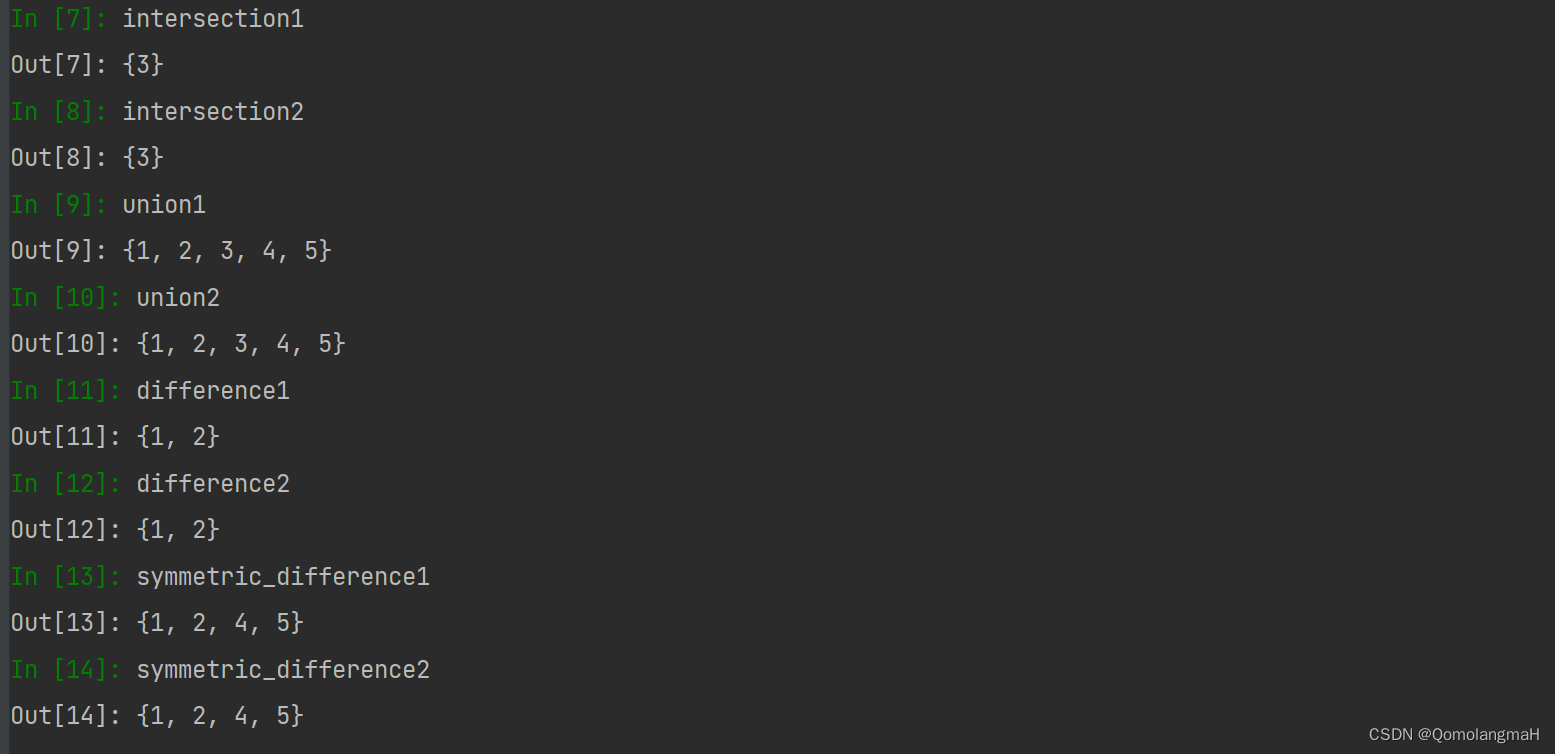
【深度学习】 Python 和 NumPy 系列教程(五):Python容器:3、集合Set详解(初始化、访问元素、常用操作、常用函数)
目录 一、前言 二、实验环境 三、Python容器(Containers) 0、容器介绍 1、列表(List) 2、元组(Tuple) 3、集合(Set) 1. 初始化 2. 访问集合元素 3. 常用操作 a. 添加单个…...

单片机C语言实例:6、定时器的应用
一、定时器0控制LED闪烁 实例程序1: #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存器的定义sbit LED P1^2; //定义LED端口/*------------------------------------------------定时器初始化子程序 …...

ChatGPT Prompting开发实战(五)
一、如何编写有效的prompt 对于大语言模型来说,编写出有效的prompt能够帮助模型更好地理解用户的意图(intents),生成针对用户提问来说是有效的答案,避免用户与模型之间来来回回对话多次但是用户不能从LLM那里得到有意义的反馈。本文通过具体…...

MySQL——DQL union合并、limit限制与DDL建表和删表
一、Union 合并 union:是实现两个查询结果的合并。 例如:当我们查询员工名字为manager 和 salesman的员工名字和 工作? select e.ename,e.job from emp e where e.jobmanager or e.job salesman; select e.ename,e.job from emp e where e.job in(man…...
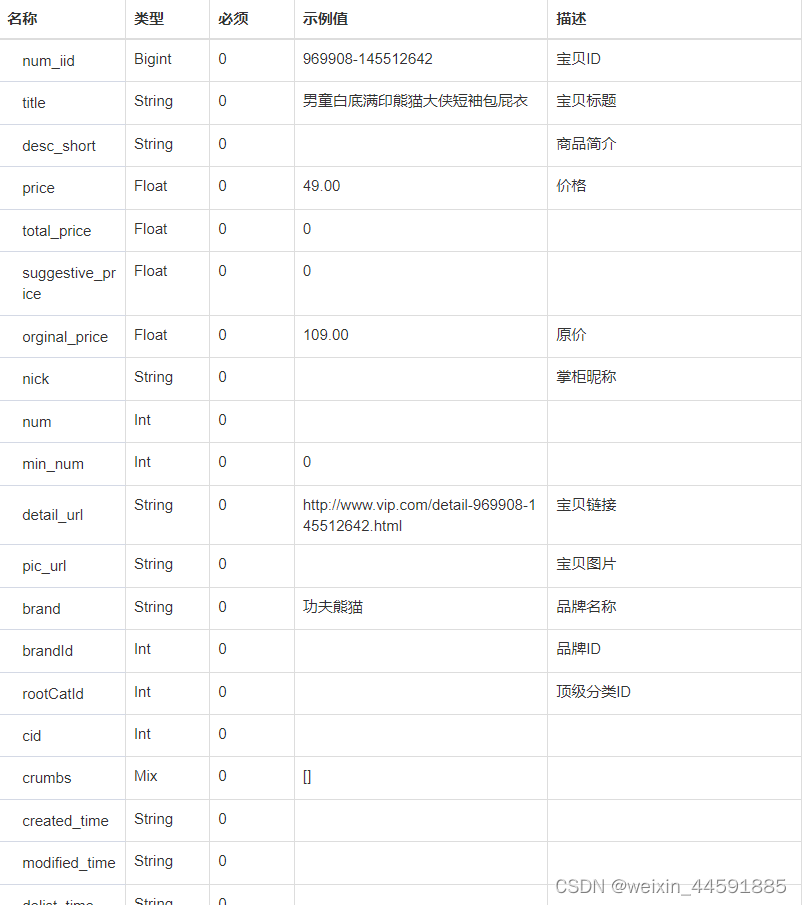
Java“牵手”唯品会商品列表数据,关键词搜索唯品会商品数据接口,唯品会API申请指南
唯品会商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取唯品会商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问唯品会商城的网页来获取商品详情信息。以下是两种常用方法的介…...
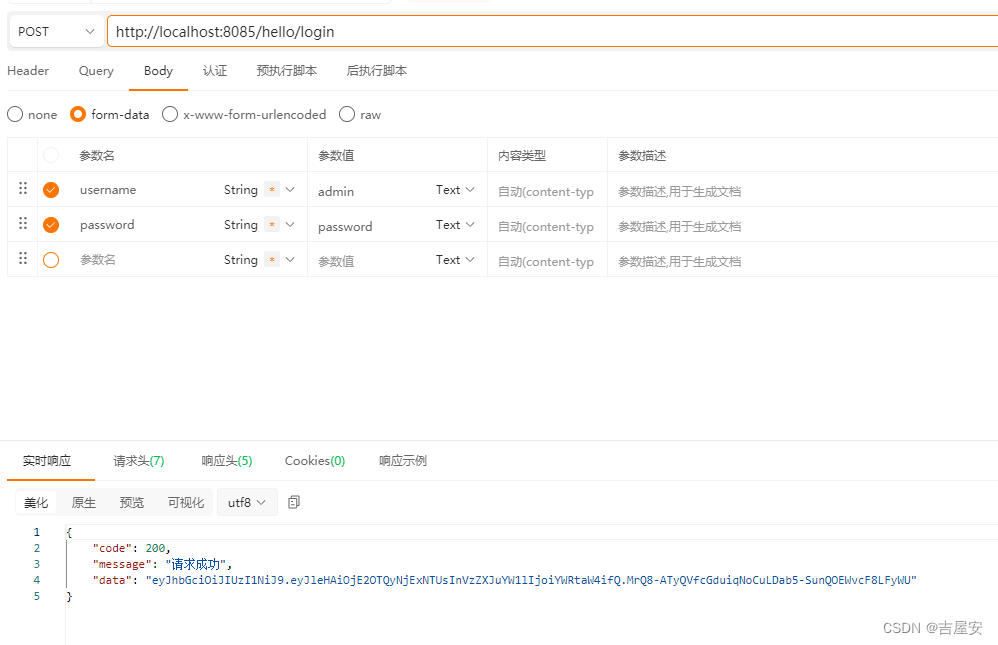
Springboot整合JWT完成验证登录
目录 一、引入依赖二、JwtUtil 代码解读三、LoginController 代码解读四、整体代码五、结果展示 一、引入依赖 <dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt</artifactId><version>0.9.1</version></depende…...

centos7 下使用docker安装常见的软件:Redis
关于docker的基础知识,请见《别在说自己不知道docker了,全文通俗易懂的给你说明白docker的基础与底层原理》 在自己学习的过程中经常会需要动手安装一下常见的工具,本篇就手把手带你用docker安装一遍。 jdk安装 如果先要更换之前的jdk从第…...
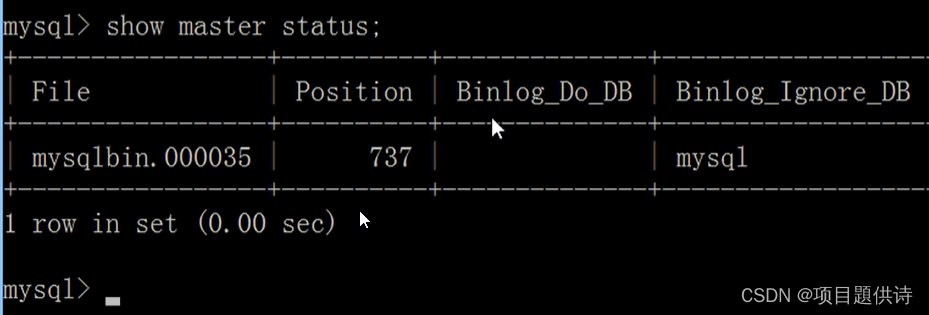
sql:SQL优化知识点记录(十五)
(1)MySQL主从复制 我们这里配置一Windows上的MySql做主机,Linux上的MySql做从机,搭建一主一从 测试以下是否能够拼通:从Linux上:167,连接Windows的165 从Windows的165 连接Linux上:…...

vue3+ts 分享海报
安装依赖1. npm install html2canvas --save<div class"flex-box"><div><div v-for"(item,index ) in from.list" :key"index" click"actvieFuntion(index)"><div>{{item}}</div><div :class"…...
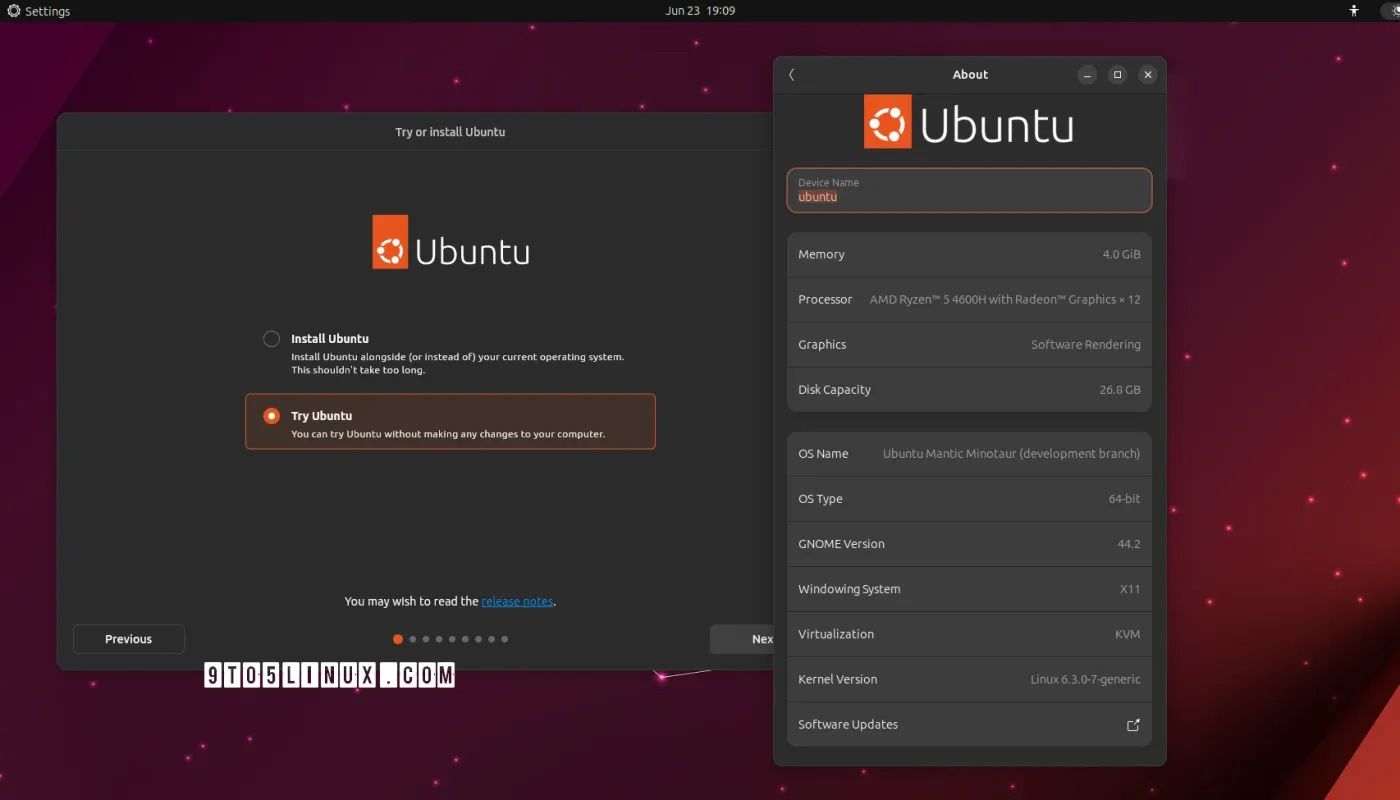
Ubuntu23.10将推出全磁盘加密功能,提高系统安全性
Canonical 宣布其即将推出的 Ubuntu 23.10(Mantic Minotaur)将引入基于 TPM 的全磁盘加密的初步支持。这个特性将利用系统可信平台模块(TPM),在系统级别上进行全磁盘加密,从而提高系统的安全性。 但需要注…...

防火墙的设置主要是为了防范什么
防火墙的设置主要是为了防范网络攻击和数据泄露。随着互联网的普及和信息化的加速,网络安全问题越来越受到人们的关注。其中,防火墙是一种常见的网络安全设备,其设置的重要性也日益凸显。 防火墙的设置主要是为了防范什么 防火墙的设置主要目…...

Vim9和其他软件的文本复制、粘贴
大家都知道:在Vim9中使用y和p命令来进行文本的复制和粘贴,今天我来说一说Vim和其他软件之间的文本复制、粘贴操作。 Vim9和其他软件进行复制、粘贴,其原理就是通过系统剪贴板作为中介来执行操作。 一、从Vim9复制文本内容 按住鼠标左键滑出…...
MySQL学习5:事务、存储引擎
事务 简介 事务是一组数据库操作的执行单元,它要么完全执行,要么完全不执行。事务是确保数据库中的数据一致性和完整性的重要机制之一。 事务具有以下四个特性(称为ACID特性): 原子性(Atomicity…...

redis如何保证接口的幂等性
背景 如何防止接口中同样的数据提交,以及如何保证消息不被重复消费,这些都是shigen在学习的过程中遇到的问题。今天,趁着在学习redis的间隙,我写了一篇文章进行简单的实现。 注意:仅使用于单机的场景,对于…...

避坑之路 —— 前后端 json 的注意问题
当我们在进行开发项目的时候,在前后端需要进行数据之间的传输,那么就会需要到json。而json算是字符串中的一种 1.先说一下前端的, 其实这两种都是表示前端希望能收到后端json这样的数据格式,那么我们在后端就需要注意将数据进行转换为json进…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
