Java“牵手”唯品会商品列表数据,关键词搜索唯品会商品数据接口,唯品会API申请指南
唯品会商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取唯品会商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问唯品会商城的网页来获取商品详情信息。以下是两种常用方法的介绍:
1. 通过唯品会开放平台接口获取商品列表和详情数据:
首先,您需要在开放平台注册成为开发者并创建一个应用,获取到所需的 App Key 和 App Secret 等信息。
使用获取到的 App Key 和 App Secret,进行签名和认证,获取 Access Token。
调用开放平台提供的接口,传入商品 ID 作为参数,获取对应商品的列表和详情页面数据。
请参考开放平台提供的接口文档,了解相应的接口和参数。
2. 直接访问唯品会商城网页并解析商品列表和商品详情数据:
使用 HTTP 请求库,发送 GET 请求到唯品会商城的商品详情页面,将关键词作为参数传递给 URL。获取到返回的 HTML 页面,根据页面结构和 DOM 操作技术,解析出商品的详细信息,例如标题、价格、销量、库存、描述、图片等。
请注意,直接解析网页可能会受到页面结构和变动的影响,需要自行编写相关的解析逻辑。
以下是一个使用 Java 编写的示例代码,展示如何通过封装 API 获取商品列表数据:
VIP.item_search - 获得关键词搜索唯品会商品列表数据返回值说明
2.1公共参数
| 名称 | 类型 | 必须 | 描述 |
|---|---|---|---|
| key | String | 是 | 调用key(必须以GET方式拼接在URL中,演示demo示例) |
| secret | String | 是 | 调用密钥 |
| api_name | String | 是 | API接口名称(包括在请求地址中)[item_search,item_get,item_search_shop等] |
| cache | String | 否 | [yes,no]默认yes,将调用缓存的数据,速度比较快 |
| result_type | String | 否 | [json,jsonu,xml,serialize,var_export]返回数据格式,默认为json,jsonu输出的内容中文可以直接阅读 |
| lang | String | 否 | [cn,en,ru]翻译语言,默认cn简体中文 |
| version | String | 否 | API版本(复制Taobaoapi2014 获取APISDK文件) |
2.2.请求示例

2.3.响应参数
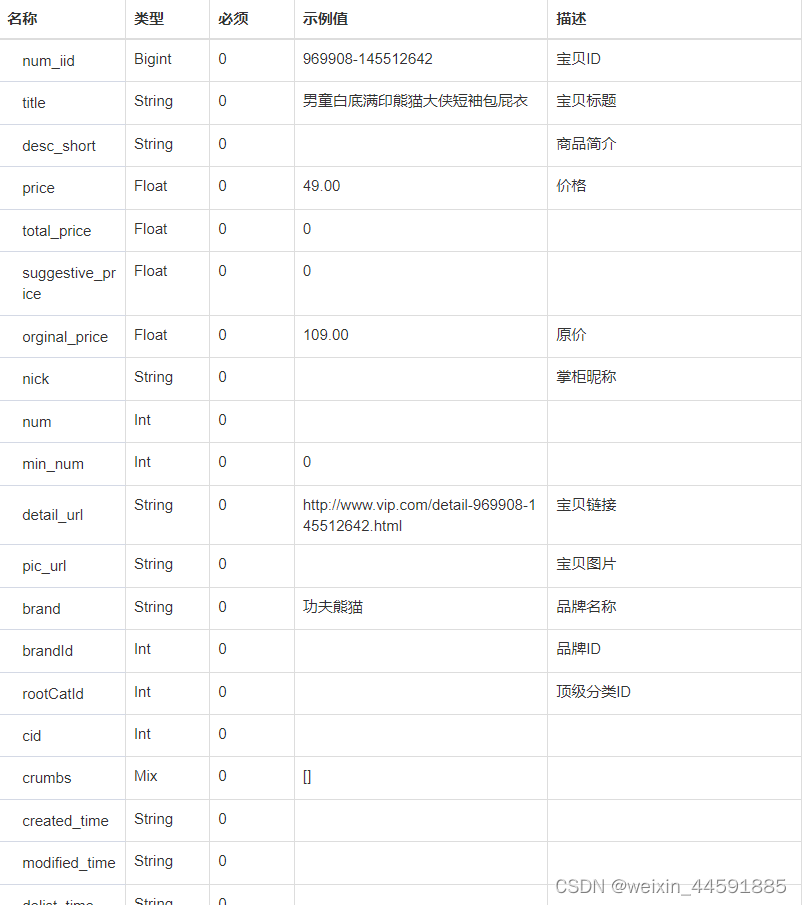
以上示例中,通过发送 HTTP /POST/GET 请求获取唯品会商品列表和详情的 API 数据,然后将返回的 JSON 数据解析为对应的数据结构,以便进一步处理和使用。请注意,实际情况中,您还需要根据 API 文档和要求来构建请求、处理异常情况和其他实现细节。
综上所述,唯品会API接口是基于开放平台的,没有开放平台就没有API接口。唯品会API接口又是更加便利的,是电商公司管理获取数据的小帮手(WeChat Taobaoapi2014)。同时,还可以通过API接口发展出跨境电商业务。唯品会API接口入点(按图搜索,商品详情,关键词搜索,商品评论,订单类接口),希望以上的示例,可以帮到有需要的朋友。
相关文章:

Java“牵手”唯品会商品列表数据,关键词搜索唯品会商品数据接口,唯品会API申请指南
唯品会商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取唯品会商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问唯品会商城的网页来获取商品详情信息。以下是两种常用方法的介…...
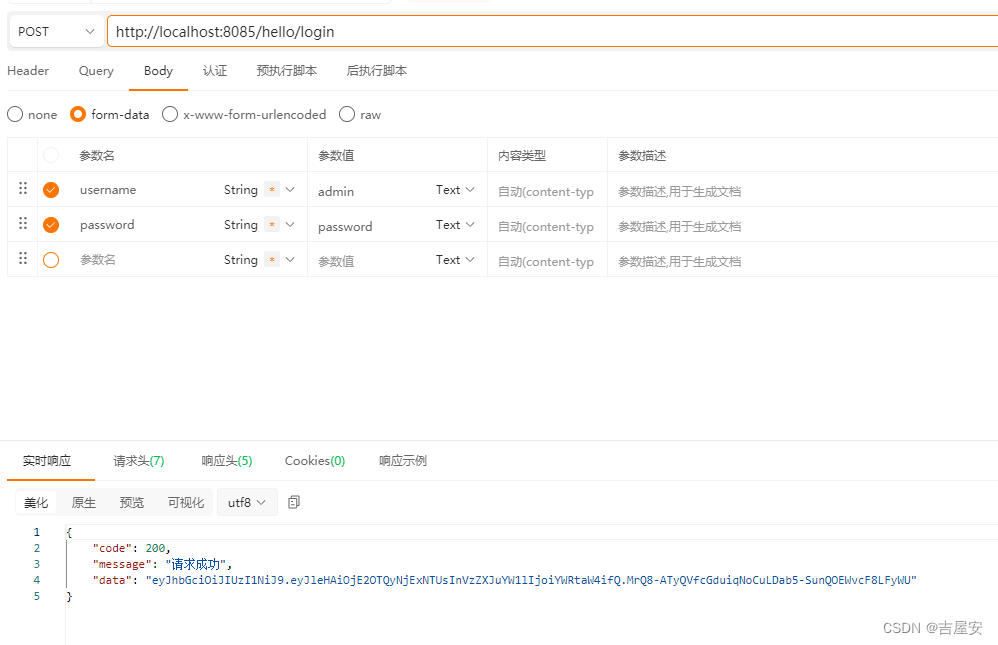
Springboot整合JWT完成验证登录
目录 一、引入依赖二、JwtUtil 代码解读三、LoginController 代码解读四、整体代码五、结果展示 一、引入依赖 <dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt</artifactId><version>0.9.1</version></depende…...

centos7 下使用docker安装常见的软件:Redis
关于docker的基础知识,请见《别在说自己不知道docker了,全文通俗易懂的给你说明白docker的基础与底层原理》 在自己学习的过程中经常会需要动手安装一下常见的工具,本篇就手把手带你用docker安装一遍。 jdk安装 如果先要更换之前的jdk从第…...
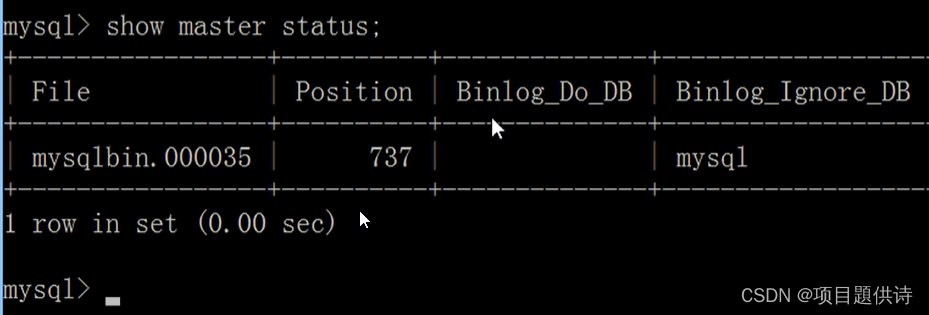
sql:SQL优化知识点记录(十五)
(1)MySQL主从复制 我们这里配置一Windows上的MySql做主机,Linux上的MySql做从机,搭建一主一从 测试以下是否能够拼通:从Linux上:167,连接Windows的165 从Windows的165 连接Linux上:…...

vue3+ts 分享海报
安装依赖1. npm install html2canvas --save<div class"flex-box"><div><div v-for"(item,index ) in from.list" :key"index" click"actvieFuntion(index)"><div>{{item}}</div><div :class"…...
Ubuntu23.10将推出全磁盘加密功能,提高系统安全性
Canonical 宣布其即将推出的 Ubuntu 23.10(Mantic Minotaur)将引入基于 TPM 的全磁盘加密的初步支持。这个特性将利用系统可信平台模块(TPM),在系统级别上进行全磁盘加密,从而提高系统的安全性。 但需要注…...

防火墙的设置主要是为了防范什么
防火墙的设置主要是为了防范网络攻击和数据泄露。随着互联网的普及和信息化的加速,网络安全问题越来越受到人们的关注。其中,防火墙是一种常见的网络安全设备,其设置的重要性也日益凸显。 防火墙的设置主要是为了防范什么 防火墙的设置主要目…...

Vim9和其他软件的文本复制、粘贴
大家都知道:在Vim9中使用y和p命令来进行文本的复制和粘贴,今天我来说一说Vim和其他软件之间的文本复制、粘贴操作。 Vim9和其他软件进行复制、粘贴,其原理就是通过系统剪贴板作为中介来执行操作。 一、从Vim9复制文本内容 按住鼠标左键滑出…...
MySQL学习5:事务、存储引擎
事务 简介 事务是一组数据库操作的执行单元,它要么完全执行,要么完全不执行。事务是确保数据库中的数据一致性和完整性的重要机制之一。 事务具有以下四个特性(称为ACID特性): 原子性(Atomicity…...

redis如何保证接口的幂等性
背景 如何防止接口中同样的数据提交,以及如何保证消息不被重复消费,这些都是shigen在学习的过程中遇到的问题。今天,趁着在学习redis的间隙,我写了一篇文章进行简单的实现。 注意:仅使用于单机的场景,对于…...

避坑之路 —— 前后端 json 的注意问题
当我们在进行开发项目的时候,在前后端需要进行数据之间的传输,那么就会需要到json。而json算是字符串中的一种 1.先说一下前端的, 其实这两种都是表示前端希望能收到后端json这样的数据格式,那么我们在后端就需要注意将数据进行转换为json进…...

[构建 Vue 组件库] 小尾巴 UI 组件库 —— 横向商品卡片(仿淘宝)
文章归档于:https://www.yuque.com/u27599042/row3c6 组件库地址 npm:https://www.npmjs.com/package/xwb-ui?activeTabreadmegitee:https://gitee.com/tongchaowei/xwb-ui 下载 npm i xwb-ui配置 按需导入 import {组件名 } from xwb-…...

【Python】Python实现五子棋游戏(带可视化界面)【独一无二】
👉博__主👈:米码收割机 👉技__能👈:C/Python语言 👉公众号👈:测试开发自动化【获取源码商业合作】 👉荣__誉👈:阿里云博客专家博主、5…...

用Maloja创建音乐收听统计数据
什么是 Maloja ? Maloja 是简单的自托管音乐记录数据库,用于创建个人收听统计数据。没有推荐,没有社交网络,没有废话。Maloja 是一个跟踪您一段时间内的收听习惯的工具。 官方演示站点:https://maloja.krateng.ch/ 导出…...

GRU门控循环单元
GRU 视频链接 https://www.bilibili.com/video/BV1Pk4y177Xg?p23&spm_id_frompageDriver&vd_source3b42b36e44d271f58e90f86679d77db7Zt—更新门 Rt—重置门 控制保存之前一层信息多,还是保留当前神经元得到的隐藏层的信息多。 Bi-GRU GRU比LSTM参数少 …...

使用Puppeteer构建博客内容的自动标签生成器
导语 标签是一种用于描述和分类博客内容的元数据,它可以帮助读者快速找到感兴趣的主题,也可以提高博客的搜索引擎优化(SEO)。然而,手动为每篇博客文章添加合适的标签是一件费时费力的工作,有时候也容易遗漏…...
大数据分析案例-基于随机森林算法构建二手房价格预测模型
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
SLAM从入门到精通(ROS安装)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 ROS科研上面用的多,实际生产其实用的也不少。它本身还是很好的应用框架。当然,它对于很多初学的同学来说还是很友好的。学完…...
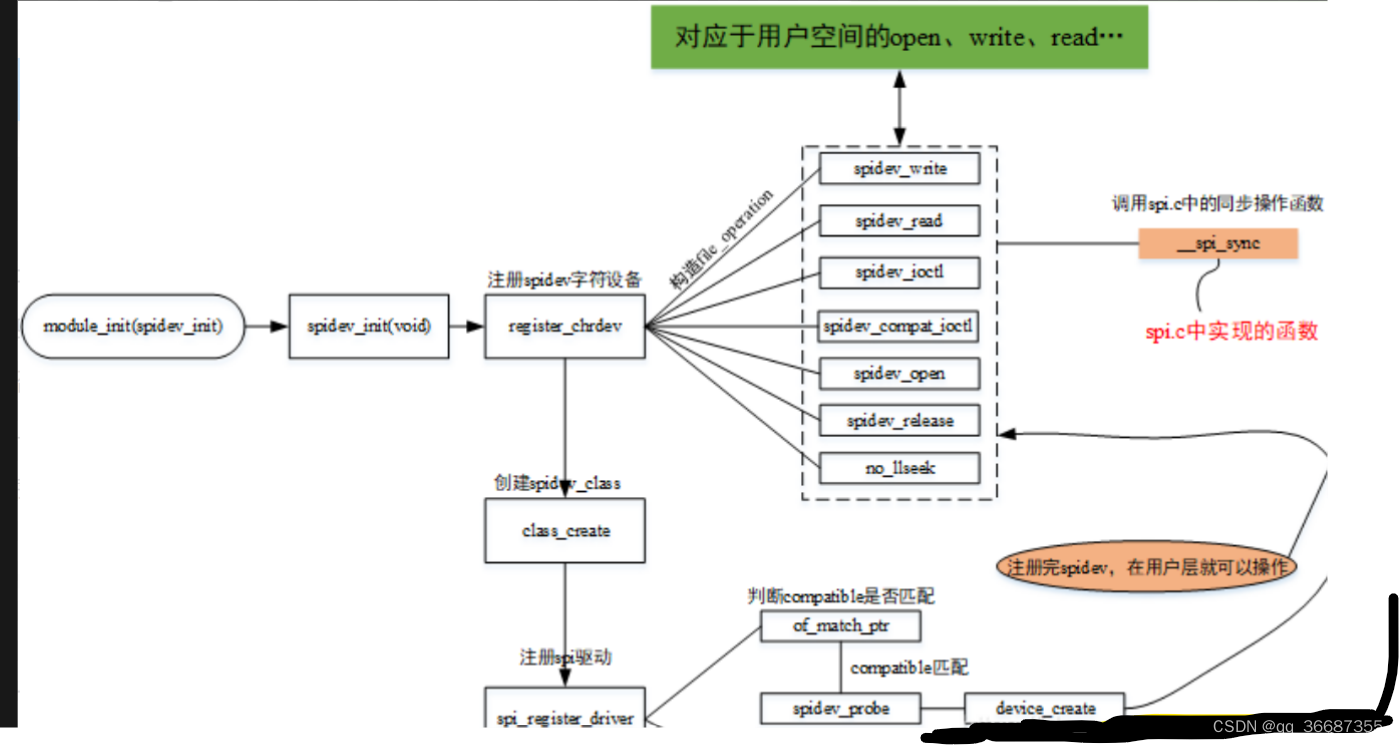
Linux 下spi设备驱动
参考: Linux kernel 有关 spi 设备树参数解析 Linux kernel 有关 spi 设备树参数解析 - 走看看 Linux SPI驱动框架(1)——核心层 Linux SPI驱动框架(1)——核心层_linux spi驱动模型_绍兴小贵宁的博客-CSDN博客 Linux SPI驱动框架(2)——控制器驱动层 Linux SPI驱…...

一:图形的位置和尺寸测量
绘制的基本要素: onDraw(Canvas):是用来重写的 Canvas:实际执行绘制的 Paint:调整粗细和颜色等 坐标系:以屏幕左上角为原点,向右、向下为正向数值的坐标系 尺寸单位:在绘制过程中所有的尺寸单位都是px…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
