算法:数组中的最大差值---“打擂台法“
文章来源:
https://blog.csdn.net/weixin_45630258/article/details/132737088
欢迎各位大佬指点、三连
1、题目:
给定一个整数数组 nums,找出给定数组中两个数字之间的最大差值。要求,第二个数字必须大于第一个数字。
2、分析特点:
求最大差值 ==> 最大值 - 最小值- 只需要遍历价格数组一遍,记录历史最小值,非最小值的考虑是最大值。
3、代码:
4、复杂度分析:
- 时间复杂度:O(n),只需要遍历一次。
- 空间复杂度:O(1),只使用了常数个变量。
5、总结:
使用打擂台的思想,遍历的时候,考虑当前值是最小值,则记录最小值,否则考虑当前值是最大值,进行更新。
6、其他解法–暴力法

6-1、复杂度分析

7、题目变化
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。

我们来假设自己来购买股票。随着时间的推移,每天我们都可以选择出售股票与否。那么,假设在第 i 天,如果我们要在今天卖股票,那么我们能赚多少钱呢?
显然,如果我们真的在买卖股票,我们肯定会想:如果我是在历史最低点买的股票就好了!太好了,在题目中,我们只要用一个变量记录一个历史最低价格 minprice,我们就可以假设自己的股票是在那天买的。那么我们在第 i 天卖出股票能得到的利润就是 prices[i] - minprice。
因此,我们只需要遍历价格数组一遍,记录历史最低点,然后在每一天考虑这么一个问题:如果我是在历史最低点买进的,那么我今天卖出能赚多少钱?当考虑完所有天数之时,我们就得到了最好的答案。
7-1、一次遍历
public int maxProfit(int prices[]) {int minprice = Integer.MAX_VALUE;int maxprofit = 0;for (int i = 0; i < prices.length; i++) {if (prices[i] < minprice) {minprice = prices[i];} else if (prices[i] - minprice > maxprofit) {maxprofit = prices[i] - minprice;}}return maxprofit;}
■ 复杂度分析:
- 时间复杂度:O(n),只需要遍历一次。
- 空间复杂度:O(1),只使用了常数个变量。
7-2、暴力法
public class Solution {public int maxProfit(int[] prices) {int maxprofit = 0;for (int i = 0; i < prices.length - 1; i++) {for (int j = i + 1; j < prices.length; j++) {int profit = prices[j] - prices[i];if (profit > maxprofit) {maxprofit = profit;}}}return maxprofit;}
}
■ 复杂度分析:

如果本文对你有帮助的话记得给一乐点个赞哦,感谢!
相关文章:

算法:数组中的最大差值---“打擂台法“
文章来源: https://blog.csdn.net/weixin_45630258/article/details/132737088 欢迎各位大佬指点、三连 1、题目: 给定一个整数数组 nums,找出给定数组中两个数字之间的最大差值。要求,第二个数字必须大于第一个数字。 2、分析特…...

三种方式查看 JVM 垃圾收集器
一、引言 不同版本的 JVM 默认使用的垃圾收集器是不同的,目前的新生代和老年代的垃圾收集器如下图所示,新生代和老年代之间的连线表示这些垃圾收集器可以进行搭配使用 垃圾收集器的名字和 JVM 里面的参数对照表如下,即在 JVM 里面并不是存储的…...
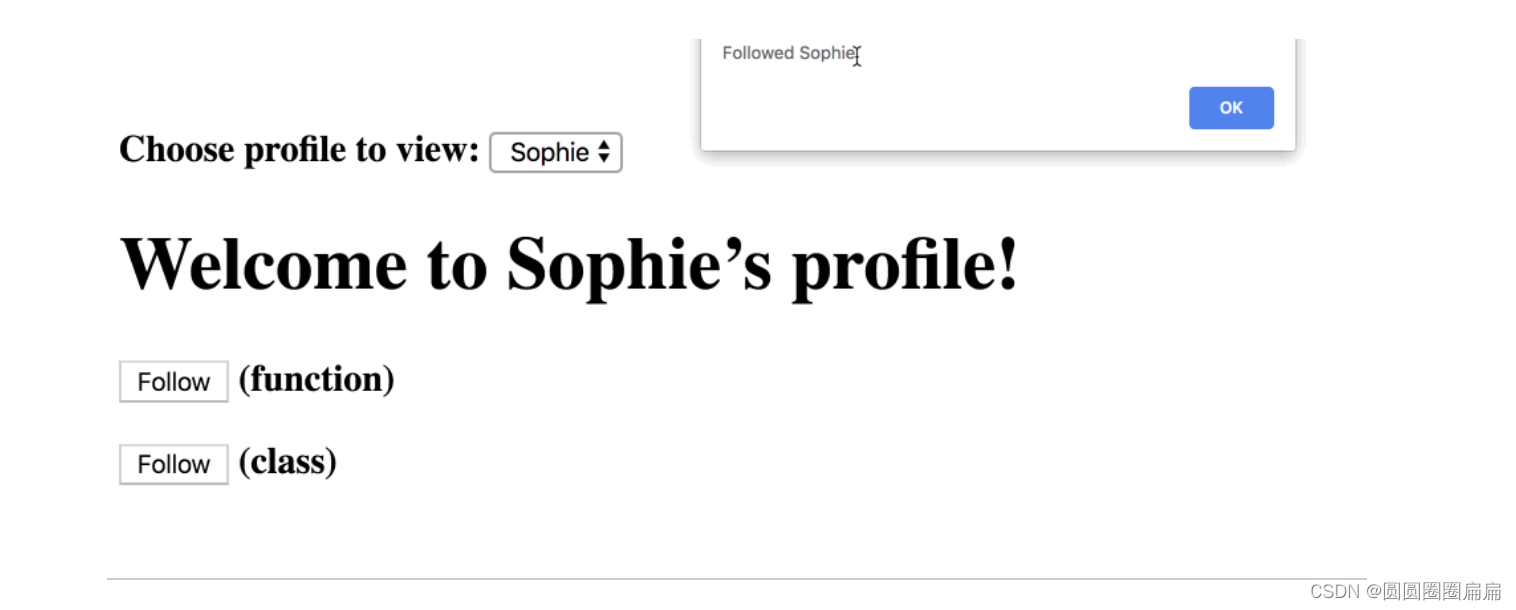
React中函数式组件与类组件有何不同?
Function Component 与 Class Component 有何不同 目录 Function Component 与 Class Component 有何不同 文章核心观点: 解释一下: 总结: 文章核心观点: Function components capture the rendered values.函数式组件捕获…...
windows11安装docker时,修改默认安装到C盘
1、修改默认安装到C盘 2、如果之前安装过docker,请删除如下目录:C:\Program Files\Docker 3、在D盘新建目录:D:\Program Files\Docker 4、winr,以管理员权限运行cmd 5、在cmd中执行如下命令,建立软联接: m…...

python模块之 aiomysql 异步mysql
mysql安装教程 mysql语法大全 python 模块pymysql模块,连接mysql数据库 一、介绍 aiomysql 是一个基于 asyncio 的异步 MySQL 客户端库,用于在 Python 中与 MySQL 数据库进行交互。它提供了异步的数据库连接和查询操作,适用于异步编程环境 …...

开开心心带你学习MySQL数据库之第八篇
索引和事务 ~~ 数据库运行的原理知识 面试题 索引 索引(index) > 目录 索引存在的意义,就是为了加快查找速度!!(省略了遍历的过程) 查找速度是快了,但是付出了一定的代价!! 1.需要付出额外的空间代价来保存索引数据 2.索引可能会拖慢新增,删除,修改的速度 ~~ …...

yml配置动态数据源(数据库@DS)与引起(If you want an embedded database (H2, HSQL or Derby))类问题
1:yml 配置 spring:datasource:dynamic:datasource:master:url: jdbc:mysql://192.168.11.50:3306/dsdd?characterEncodingUTF-8&useUnicodetrue&useSSLfalse&tinyInt1isBitfalse&allowPublicKeyRetrievaltrue&serverTimezoneUTCusername: ro…...

yolov5运行过程遇到的小问题(随时更新)
1.关于git的问题 解决办法:插入下面代码 import os os.environ["GIT_PYTHON_REFRESH"] "quiet"2.页面太小无法完成操作 解决办法: 如果不好使再考虑降低Batch_Size大小或者调整虚拟内存可用硬盘空间大小!(调整虚拟内存…...

使用FabricJS创建Image对象的JSON表示
本篇文章介绍一下如何创建图像的 JSON 表示形式 使用 FabricJS 的对象。我们可以通过创建一个实例来创建一个 Image 对象 织物.图像。由于它是FabricJS的基本元素之一,我们也可以轻松地 通过应用角度、不透明度等属性来自定义它。为了创建 JSON Image 对象的表示&am…...

【牛客刷题】反转固定区间链表、每k个节点一组反转
链表内指定区间反转_牛客题霸_牛客网 ListNode* reverseList(ListNode* head, ListNode* tail) {ListNode* pre nullptr;ListNode* cur head;while (cur ! tail) { 最后cur就是tailListNode* temp cur->next;cur->next pre;pre cur;cur temp;}return pre;}ListNode…...

算法:数组常见套路1---双指针、取模、打擂台法
文章来源: https://blog.csdn.net/weixin_45630258/article/details/132738318 欢迎各位大佬指点、三连 一、数组的合并–双指针[快慢指针] 1、题目: 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ࿰…...

App 出海实践:Google Play 结算系统
作者:业志陈 现如今,App 出海热度不减,是很多公司和个人开发者选择的一个市场方向。App 为了实现盈利,除了接入广告这种最常见的变现方式外,就是通过提供各类虚拟商品或者是会员服务来吸引用户付费了,此时 …...

国际慈善日 | 追寻大爱无疆,拓世科技集团的公益之路
每年的9月5日,是联合国大会正式选定的国际慈善日。这一天的设立,旨在通过提高公众对慈善活动的意识,鼓励慈善公益活动通过各种形式在全球范围内得到增强和发展。这是一个向慈善公益事业致敬的日子,同时也是呼吁全球团结一致共同发…...

关于DNS的一些认识
目录 什么是DNS? 一台具有单个DNS的机器可以拥有多个地址吗? 一台计算机可以有多个属于不同顶级域的DNS名字吗? 什么是DNS? DNS是域名系统(Domain Name System)的缩写,它是互联网中用于将域名…...

游戏性能优化
Unity性能优化主要包括以下方面: 1.渲染性能 。包括减少Draw Calls、减少三角面数、使用LOD、使用批处理技术、减少实时光源等,以提高游戏的帧率和渲染效率。 2.内存性能 。包括使用对象池、使用合适的纹理、使用异步加载资源等,以减少内存占…...
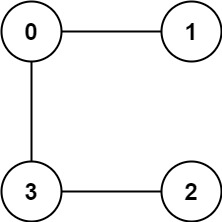
公开游戏、基于有向图的游戏
目录 〇,背景 一,公开游戏、策梅洛定理 1,公开游戏 2,策梅洛定理 二,有向图游戏 1,狭义有向图游戏 2,广义有向图游戏 3,狭义有向图游戏的SG数 4,Bash Game 力扣…...

CSS学习笔记05
CSS笔记05 定位 position CSS 属性position - 用于指定一个元素在文档中的定位方式。top,right,bottom 和 left 属性则决定了该元素的最终位置。position 有以下常用的属性值: position: static; - 默认值。指定元素使用正常的布局行为&am…...

Linux查看指定端口是否被占用
在Linux中,可以使用多种方法来检查一个特定端口(例如3306,通常由MySQL使用)是否被占用: 使用netstat命令: 如果系统中已安装了netstat,可以使用以下命令检查3306端口: netstat -tuln | grep 330…...

【Python 自动化】小说推文一键生成思路概述
最近看了一下小说推文成品软件的思路,发现可以完全迁移到我的 BookerAutoVideo 上面来。这篇短文里面,我试着分析一下整个推文视频生成的流程,以及简要阐述一下有什么工具。 整体流程是这样: 分句 原文是按照段落组织的…...

MySQL中的字符集与排序规则详解
在 MySQL 中,字符集(Character Set)用于确定可以在数据库中存储的字符集合,而排序规则(Collation)用于指定比较和排序字符串的规则。下面是关于 MySQL 中字符集和排序规则的一些详细信息: 字符集…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
