常見算法時間複雜度分析
当我们进行算法分析时,通常会忽略掉常数倍数的因子和低阶项,只考虑最高阶的项。这是因为在大规模问题下,较小的项和常数倍数的因子相对于最高阶的项来说变得可以忽略不计。
以下是一些常见的示例,说明了常数倍数的因子和高阶项对算法的影响:
O(2n) 和 O(n):在 O(2n) 中,常数倍数因子为 2,而在 O(n) 中为 1。但是,当 n 变得非常大时,2n 和 n 之间的差距就变得微不足道,因此我们可以说 O(2n) 等价于 O(n)O(3n^2) 和 O(n^2):在 O(3n^2) 中,常数倍数因子为 3,而在 O(n^2) 中为 1。但是,当 n 变得非常大时,3n^2 和 n^2 之间的差距就变得微不足道,因此我们可以说 O(3n^2) 等价于 O(n^2)O(n^2 + n) 和 O(n^2):在 O(n^2 + n) 中,我们有两个项,分别是 n^2 和 n。然而,在大规模问题下,n 这样的低阶项可以被 n^2 这样的高阶项主导,因此我们可以忽略掉 n,即 O(n^2 + n) 等价于 O(n^2)O(n^3 + n^2) 和 O(n^3):在 O(n^3 + n^2) 中,我们有两个项,分别是 n^3 和 n^2。同样,在大规模问题下,n^2 这样的低阶项可以被 n^3 这样的高阶项主导,因此我们可以忽略掉 n^2,即 O(n^3 + n^2) 等价于 O(n^3)
通过忽略常数倍数的因子和低阶项,我们可以简化算法的复杂度表示,并更好地理解算法的增长趋势和相对性能。这种简化使得我们能够更容易地比较和分析不同算法之间的效率。
冒泡排序
基本的冒泡排序算法
public static void bubbleSort(int[] arr) {int n = arr.length;for (int i = 0; i < n - 1; i++) {for (int j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {// 交换arr[j]和arr[j+1]int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}
最坏时间复杂度是O(n^2)
即当输入的序列是降序排列时,每次比较都需要进行交换操作。在最坏情况下,共进行了(n-1)+(n-2)+…+2+1 = n*(n-1)/2次比较和交换,时间复杂度为O(n^2)
最好时间复杂度是O(n)
1、在最好的情况下,即当输入的序列已经是升序排列时,冒泡排序只需要进行一遍比较即可完成排序。
2、但是根据上面代码,无论输入序列是否有序,冒泡排序都将进行n*(n-1)/2次比较,时间复杂度为O(n^2)。
3、其实,最好情况下的时间复杂度O(n)通常是指在某些优化的冒泡排序算法中,如果发现某一轮比较中没有交换操作,就可以提前结束排序。
/*** 改进版冒泡排序* @param arr*/public static void improvedBubbleSort(int[] arr) {int n = arr.length;boolean swapped;for (int i = 0; i < n - 1; i++) {swapped = false;for (int j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {// 交换arr[j]和arr[j+1]int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;swapped = true;}}// 如果某轮比较没有发生交换,说明已经有序,提前结束排序if (!swapped) {break;}}}
選擇排序
快速排序
public class QuickSort {public static void main(String[] args) {int[] arr = {7, 2, 1, 6, 8, 5, 3, 4};quickSort(arr, 0, arr.length - 1);for (int num : arr) {System.out.print(num + " ");}}public static void quickSort(int[] arr, int low, int high) {if (low < high) {// 分区操作,将数组分为两部分,返回基准元素的索引int pivot = partition(arr, low, high);// 对左子数组进行快速排序quickSort(arr, low, pivot - 1);// 对右子数组进行快速排序quickSort(arr, pivot + 1, high);}}public static int partition(int[] arr, int low, int high) {// 选择最后一个元素作为基准int pivot = arr[high];// i 指向小于基准的元素的位置int i = low - 1;// 遍历数组,将小于基准的元素移动到基准的左边for (int j = low; j < high; j++) {if (arr[j] < pivot) {i++;swap(arr, i, j);}}// 将基准元素放到正确的位置上swap(arr, i + 1, high);// 返回基准元素的索引return i + 1;}public static void swap(int[] arr, int i, int j) {// 交换数组中两个元素的位置int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
}
最好时间复杂度是O(nlogn)
快速排序的最好情况下,每次划分都能将待排序序列分成长度为 n/2 的两个子序列。假设递归树的深度为 d,初始时,序列的长度为 n。每次划分后,序列的长度变为原来的一半,即 n/2。那么经过 d 次划分后,序列的长度变为 n/(2^d)。当划分完毕后,序列的长度为 1。
所以我们有以下等式:n/(2^d) = 1
通过移项,可以得到:
n = 2^d
取以 2 为底的对数,我们得到:
d = log2(n)
此时递归树的深度为 log2n,每层的时间复杂度为O(n),因此最好情况下的时间复杂度为O(nlogn)
-
在算法分析中,我们通常只关注时间复杂度的增长趋势,而不是具体的常数因子或底数。因此,在常见的情况下,会省略对数的底数,并将时间复杂度简化为O(n log n)。
-
对数的底数对于增长趋势的影响较小。对于底数为2的对数(log2n)和底数为10的对数(log10n)来说,它们之间的差异只是一个常数因子,而不会改变时间复杂度的增长趋势。
-
深度算法:
最坏时间复杂度是O(n^2)
快速排序的最坏情况下,每次划分都将待排序序列分为长度为 1 和 n-1 的两个子序列,此时递归树的深度为 n,每层的时间复杂度为O(n),因此最坏情况下的时间复杂度为O(n^2)
归并排序
希尔排序
相关文章:

常見算法時間複雜度分析
当我们进行算法分析时,通常会忽略掉常数倍数的因子和低阶项,只考虑最高阶的项。这是因为在大规模问题下,较小的项和常数倍数的因子相对于最高阶的项来说变得可以忽略不计。 以下是一些常见的示例,说明了常数倍数的因子和高阶项对…...

自学Python05-学会Python中的函数定义
亲爱的同学们,今天我们将开始学习 Python 中的函数。函数就像一个魔法盒子,可以让我们在程序中执行一段代码,并且可以反复使用。这样,我们的程序就可以变得更加简洁和易于理解。现在,让我们一起来学习如何使用函数吧&a…...
)
设计模式-组合模式(Composite)
文章目录 前言一、组合模式的概念二、组合模式的优缺点1.优点2.缺点 三、组合模式的实现总结 前言 组合模式(Composite Pattern)是一种结构型设计模式,它允许你将对象组合成树状结构以表示“整体-部分”的层次结构。组合模式使得客户端可以统…...

架构核心技术之微服务架构
小熊学Java:https://www.javaxiaobear.cn/,文末有免费资源 本文我们来学习微服务的架构设计 主要包括如下内容。 单体系统的困难:编译部署困难、数据库连接耗尽、服务复用困难、新增业务困难。 微服务框架:Dubbo 和 Spring Clou…...
SQL Server2022版+SSMS安装教程(保姆级)
SQL Server2022版SSMS安装教程(保姆级) 一,安装SQL Server数据库 1.下载安装包 (1)百度网盘下载安装包 链接:https://pan.baidu.com/s/1A-WRVES4EGv8EVArGNF2QQ?pwd6uvs 提取码:6uvs &…...
go语言基础---8
Http请求报文格式分析 package mainimport ("fmt""net" )func main() {//监听listener, err : net.Listen("tcp", ":8000")if err ! nil {fmt.Println("listener err", err)return}defer listener.Close()//阻塞等待用户的…...

Oracle的 dblink 学习笔记
文章目录 一、基础环境二、适用场景三、过程和方法四、参考资料 版权声明:本文为CSDN博主「杨群」的原创文章,遵循 CC 4.0 BY-SA版权协议,于2023年9月10日首发于CSDN,转载请附上原文出处链接及本声明。 原文链接:http…...

任意文件上传
1.任意文件上传概述 1.1 漏洞成因 服务器配置不当,开启了PUT 方法。 Web 应用开放了文件上传功能,没有对上传的文件做足够的限制和过滤。在程序开发部署时,没有考虑以下因素,导致限制被绕过: 代码特性 组件漏洞&am…...

【Unity3D】UI Toolkit自定义元素
1 前言 UI Toolkit 支持通过继承 VisualElement 实现自定义元素,便于通过脚本控制元素。另外,UI Toolkit 也支持将一个容器及其所有子元素作为一个模板,便于通过脚本复制模板。 如果读者对 UI Toolkit 不是太了解,可以参考以下内容…...
layui手机端使用laydate时间选择器被输入法遮挡的解决方案
在HTML中,你可以使用input元素的readonly属性来禁止用户输入,但是这将完全禁用输入,而不仅仅是禁止弹出输入法。如果你想允许用户在特定条件下输入,你可以使用JavaScript来动态地切换readonly属性。 readonly属性 增加readonly属…...

MVSNet CVPR-2018 学习总结笔记 译文 深度学习三维重建
文章目录 2 MVSNet CVPR-20182.0 主要特点2.1 过程2.2 MVSNet主要贡献2.3 论文简介2.3.1 深度特征提取2.3.2 构造匹配代价2.3.3 代价累计2.3.4 深度估计2.3.5 深度图优化2.4 MVSNet(pytorch版本)2 MVSNet CVPR-2018 MVSNet (pytorch版) 代码注释版 下载 (注释非常详细,代码…...
Kafka/Spark-01消费topic到写出到topic
1 Kafka的工具类 1.1 从kafka消费数据的方法 消费者代码 def getKafkaDStream(ssc : StreamingContext , topic: String , groupId:String ) {consumerConfigs.put(ConsumerConfig.GROUP_ID_CONFIG , groupId)val kafkaDStream: InputDStream[ConsumerRecord[String, Strin…...
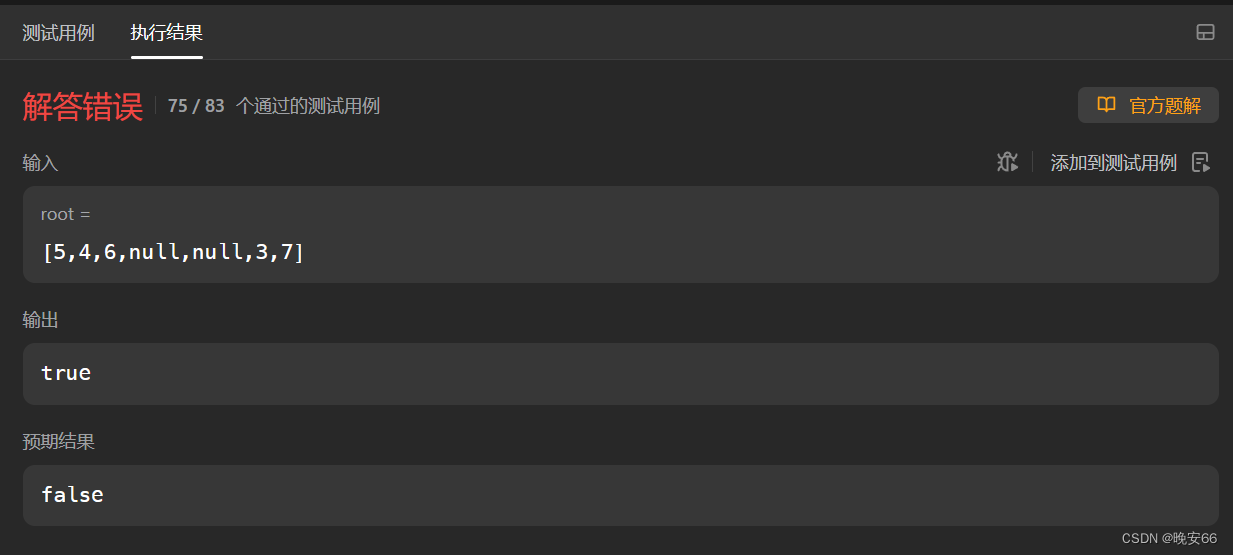
【算法与数据结构】98、LeetCode验证二叉搜索树
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:注意不要落入下面你的陷阱,笔者本来想左节点键值<中间节点键值<右节点键值即可&…...
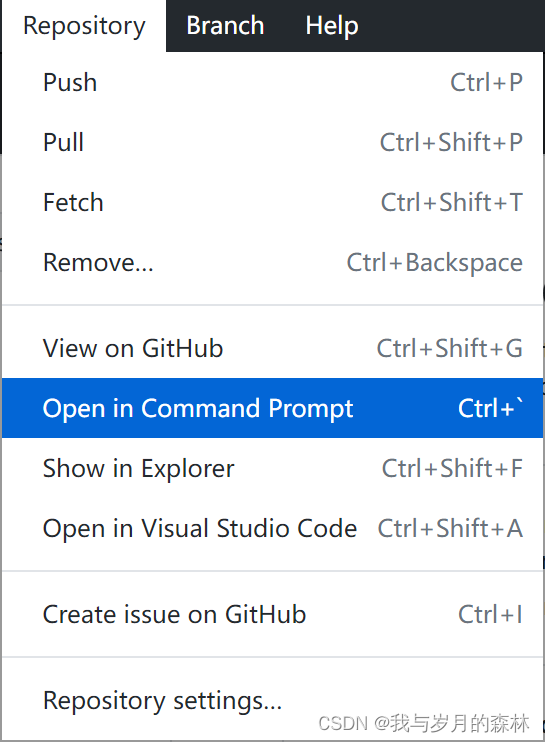
关于GitHub Desktop中的“Open in Git Bash”无法使用的问题
问题描述 在GitHub Desktop中选择Repository--Open in Git Bash(如图1),出现如图2所示结果。 图1 图2 解决办法(Windows10) 这个问题是由于Git的环境变量没有得到正确配置所导致的,所以需要正确设置环境变量…...

使用DeepSpeed加速大型模型训练(二)
使用DeepSpeed加速大型模型训练 在这篇文章中,我们将了解如何利用Accelerate库来训练大型模型,从而使用户能够利用DeeSpeed的 ZeRO 功能。 简介 尝试训练大型模型时是否厌倦了内存不足 (OOM) 错误?我们已经为您提供了保障。大型模型性能非…...

ASP.net web应用 GridView控件常用方法
GridView 控件是 ASP.NET Web Forms 中常用的数据展示控件之一。它提供了一个网格形式的表格,用于显示和编辑数据。GridView 控件对于包含大量数据、需要进行分页、排序和筛选的情况非常有用。 GridView 控件的主要特性包括: 数据绑定:GridV…...

MATLAB入门一基础知识
MATLAB入门一基础知识 此篇为课程学习笔记 链接: link 什么是MATLAB 平时所说的MATLAB既是一款软件又是一种编程语言,只是这种高级解释性语言是在配套的软件下进行开发的 MATLAB的一个特性 MATLAB的一个特性,如果一条语句以英文分号‘;’结尾&…...

SpringMVC实现文件上传和下载功能
文件下载 ResponseEntity用于控制器方法的返回值类型,该控制器方法的返回值就是响应到浏览器的响应报文。具体步骤如下: 获取下载文件的位置;创建流,读取文件;设置响应信息,包括响应头,响应体以…...
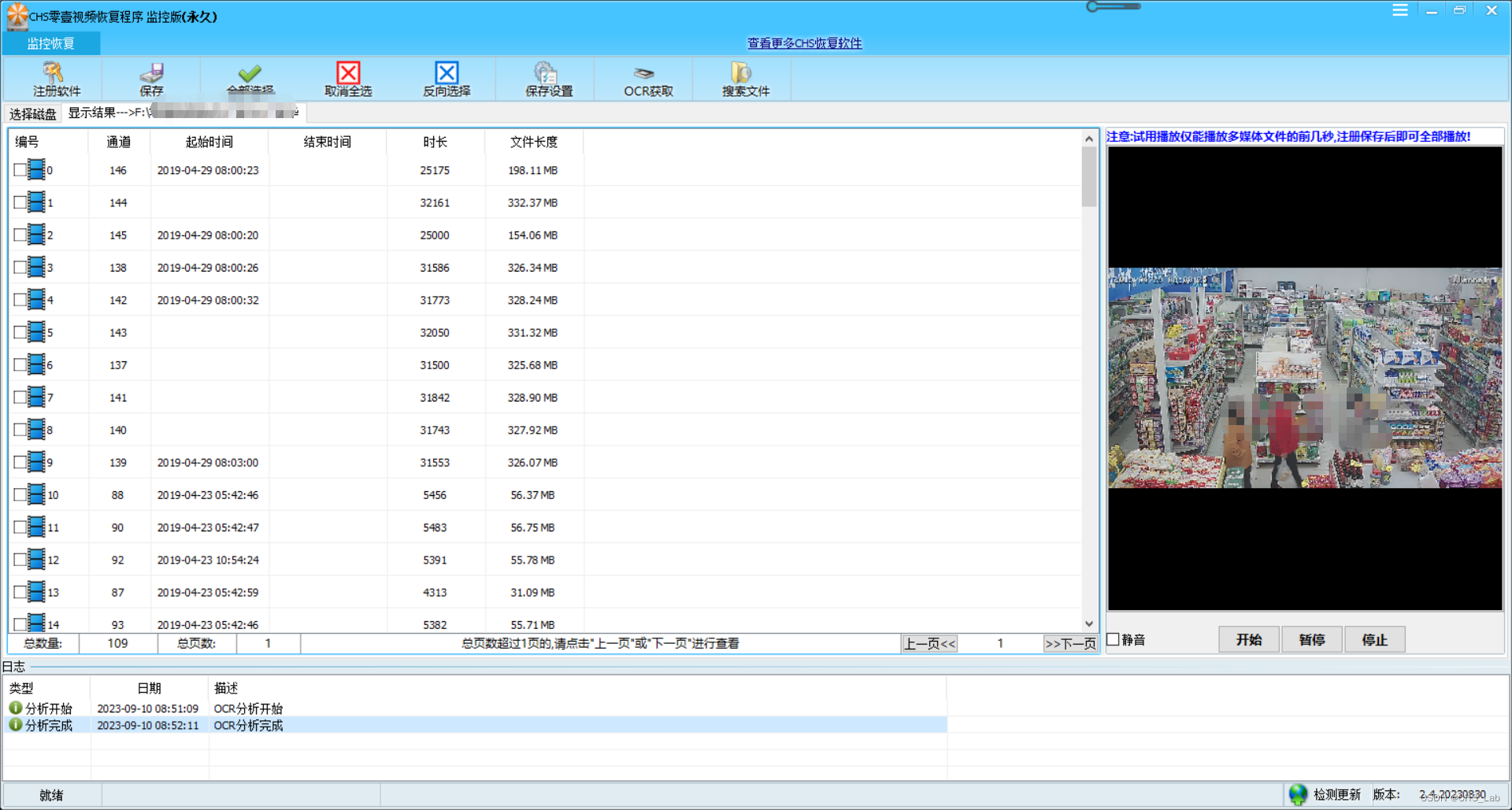
CHS零壹视频恢复程序OCR使用方法
目前CHS零壹视频恢复程序监控版、专业版、高级版已经支持了OCR,OCR是一种光学识别系统,通俗说就和扫描仪带的OCR软件一样的原理: 分析照片->OCR获取字符串->整理字符串->输出 使用方法如下(以CHS零壹视频恢复程序监控版…...

云备份——服务端客户端联合测试
一,准备工作 服务端清空备份文件信息、备份文件夹、压缩文件夹 客户端清空备份文件夹 二,开始测试 服务端配置文件 先启动服务端和客户端 向客户端指定文件夹放入稍微大点的文件,方便后续测试断点重传 2.1 上传功能测试 客户端自动上传成功…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
