Redis带你深入学习数据类型set
目录
1、set
2、set相关命令
2.1、添加元素 sadd
2.2、获取元素 smembers
2.3、判断元素是否存在 sismember
2.4、获取set中元素数量 scard
2.5、删除元素spop、srem
2.6、移动元素smove
2.7、集合中相关命令:sinter、sinterstore、sunion、sunionstore、sdiff、sdiffstore
3、应用场景
1、set
set数据类型的特点;
- set中的元素是无序的
- set中的元素不能重复
- set中支持多个几个取交集并集差集等~
2、set相关命令
2.1、添加元素 sadd
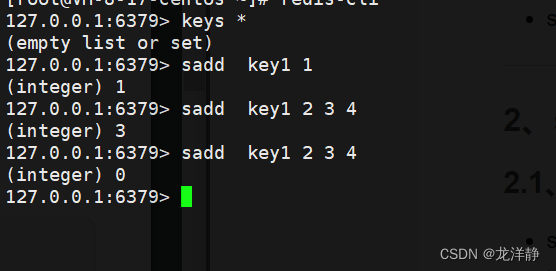
- sadd:往集合中添加元素;重复元素无法添加到集合中
- 语法:sadd key member [member ...]
- 返回值:成功添加元素的个数(集合已经存在的元素,再次添加不算为添加成功)
- 时间复杂度O(1)
举例:
2.2、获取元素 smembers
- smembers:获取一个key中的所有元素;元素顺序是无序的
- 语法:smembers key
- 返回值:集合中的所有元素
- 时间复杂度O(1)
举例:
2.3、判断元素是否存在 sismember
- sismember:
- 语法:
- 返回值:
- 时间复杂度
举例:

注:当集合中存放的都是整数,且数量不是特别多的情况下,内部编码是intset,此时虽然是无序的,但我本人猜测可能还是有处理的,相对来说还是有序的,从小到大 排列~
当内部编码是hashtable时,就是完全无序了~
2.4、获取set中元素数量 scard
- scard:获取一个set的基数,也就是set中的元素个数
- 语法:scard key
- 返回值:set内的元素的个数
- 时间复杂度O(1)
举例:

2.5、删除元素spop、srem
spop: 随机删除一个或多个元素,由于set中元素是无序的,所以具体删除哪个元素也是随机的
- 语法:spop key [count] 【不带参数默认为1】
- 返回值:被删除的元素的值
- 时间复杂度O(n) --- n->count
举例:

srem:删除集合中指定的元素
- 语法:srem key member [member...]
- 返回值:成功删除的元素个数
- 时间复杂度O(k)---被删除的个数~
举例:

2.6、移动元素smove
- smove:将一个元素从一个集合中移动到另一个集合中~
- 语法:smove source destination member
- 返回值:命令执行成功返回1;失败返回0
- 时间复杂度O(1)
举例:

2.7、集合中相关命令:sinter、sinterstore、sunion、sunionstore、sdiff、sdiffstore
sinter:获取指定set的交集中的元素
举例:

- 语法:sinter key [key...]
- 返回值:交集的元素
- 时间复杂度O(n*m)---->n是最小的集合元素个数,m是最大的集合元素个数
sinterstore:获取指定set的交集中的元素并保存到另一个指定集合set中
举例:
- 语法:sinterstore destination key [key...]
- 返回值:交集元素个数
- 时间复杂度O(n*m)---->n是最小的集合元素个数,m是最大的集合元素个数

sunion:获取指定的集合set的并集中的元素
- 语法:sunion key [key...]
- 返回值:并集的元素
- 时间复杂度O(N)---N为指定的所有的集合set的总的元素个数
举例:

sunionstore:获取指定的集合set的并集中的元素并保存到指定的目标集合set中
- 语法:sunionstore
- 返回值:并集的元素个数
- 时间复杂度O(N)---N为指定的所有的集合set的总的元素个数
举例:

sdiff:获取指定的集合set的差集中元素
- 语法:sdiff key [key...]
- 返回值:差集的元素
- 时间复杂度O(N)---N为指定的所有的集合set的总的元素个数
举例:

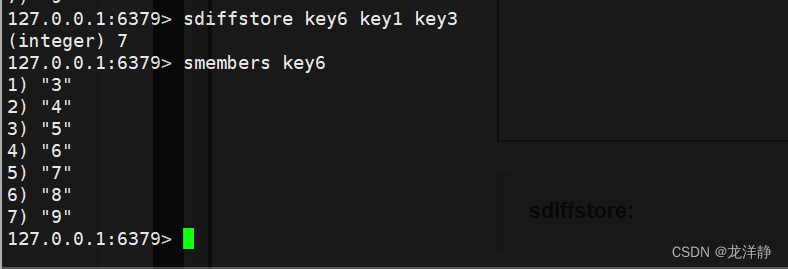
sdiffstore:
- 语法:sdiffstore
- 返回值:差集的元素个数
- 时间复杂度O(N)---N为指定的所有的集合set的总的元素个数
举例:
3、应用场景
3.1、使用set来保存用户的标签
例如最常见的“人物画像”,给相应的用户打上对应标签后,针对性给该用户推送他可能感兴趣的话题
或者例如:我们博客网站常常使用到的兴趣标签,把一个个有着相同爱好,关注类似内容的用户利用一个标签把他们进行归并
3.2、使用set计算用户间的共同好友
共同好友功能,共同喜好,或者可以引申到二度好友之类的扩展应用
例如QQ中有一个功能叫做你可能认识的人~
3.3、使用set统计UV
PV:用户每次访问某一个服务器时,都会产生一个pv
UV:用户访问服务器,会产生一个UV,但同一个多次访问不会使UV增加,所以使用set统计UV,能够很好的做到去重~
好啦,下期见啦~
相关文章:

Redis带你深入学习数据类型set
目录 1、set 2、set相关命令 2.1、添加元素 sadd 2.2、获取元素 smembers 2.3、判断元素是否存在 sismember 2.4、获取set中元素数量 scard 2.5、删除元素spop、srem 2.6、移动元素smove 2.7、集合中相关命令:sinter、sinterstore、sunion、sunionstore、s…...

Json“牵手”易贝商品详情数据方法,易贝商品详情API接口,易贝API申请指南
易贝是一个可让全球民众在网上买卖物品的线上拍卖及购物网站,易贝(EBAY)于1995年9月4日由Pierre Omidyar以Auctionweb的名称创立于加利福尼亚州圣荷塞。人们可以在易贝上通过网络出售商品。2014年2月20日,易贝宣布收购3D虚拟试衣公…...
《AI一键生成抖音商品种草文案》让你秒变带货王!
在这个数字化的时代,我们的生活被各种应用所包围,其中,抖音作为一款短视频分享平台,已经成为了我们生活中不可或缺的一部分。然而,作为一名抖音创作者,你是否曾经遇到过这样的困扰:在创作商品种…...

博客系统(升级(Spring))(二)获取当前用户信息、对密码进行加密、设置统一数据格式、设置未登录拦截、线程池
博客系统(二) 博客系统获取当前用户的信息对密码进行加密和解密的操作设置统一的数据返回格式设置未登录拦截设置线程池 博客系统 博客系统是干什么的? CSDN就是一个典型的博客系统。而我在这里就是通过模拟实现一个博客系统,这是…...

Postman接口测试工具
Postman接口测试工具 Postman简介Postman 发送一个请求postman创建一个集合Postman 快捷键Postman设置postman请求postman历史postman请求排错postman集合简介postman创建和共享集合postman管理集合postman数据导入导出postman测试脚本postman环境变量和全局变量...

appium+jenkins实例构建
自动化测试平台 Jenkins简介 是一个开源软件项目,是基于java开发的一种持续集成工具,用于监控持续重复的工作,旨在提供一个开放易用的软件平台,使软件的持续集成变成可能。 前面我们已经开完测试脚本,也使用bat 批处…...
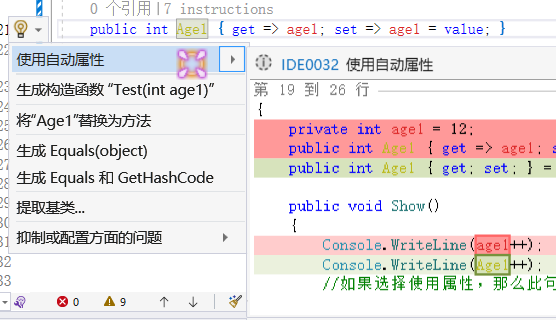
c#中字段和属性的区别,委托和事件的区别
IDE眼里的字段和属性 class Test {public int age1 12;public int Age2 { get; set; } 18;public void Show(){Console.WriteLine(age1);Console.WriteLine(Age2);} }很多新人发现在类中定义变量时,有些人会在后面写上get,set。 这种写法定义出来的变量…...
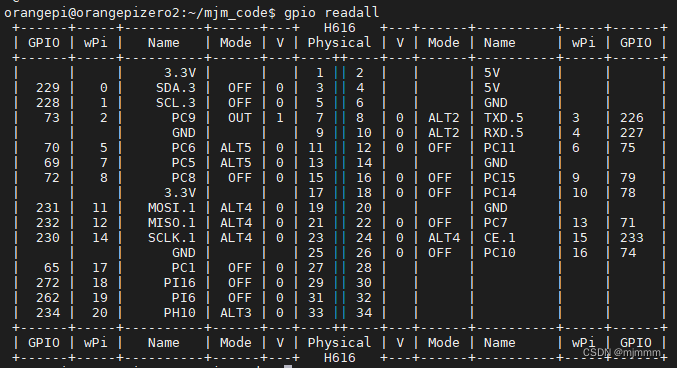
香橙派使用外设驱动库wiringOP来驱动蜂鸣器
硬件接线 回顾香橙派的物理引脚对应: 所以将VCC接到1,GND接到6,I/O口接到7: 代码编写 香橙派的wiringOP库提供了很多的例程,可以将blink.c拷贝进自己的代码文件夹来修改: 小插曲---将手动对齐的Tab和自动对…...

微信小程序Day3笔记
1、页面导航 1. 什么是页面导航 页面导航指的是页面之间的相互跳转。例如:浏览器中实现页面导航的方式有如下两种: <a>链接location.href 2. 小程序中实现页面导航的两种方式: 声明式导航: 在页面上声明一个<navigat…...

大数据技术之Hadoop:提交MapReduce任务到YARN执行(八)
目录 一、前言 二、示例程序 2.1 提交wordcount示例程序 2.2 提交求圆周率示例程序 三、写在最后 一、前言 我们前面提到了MapReduce,也说了现在几乎没有人再写MapReduce代码了,因为它已经过时了。然而不写代码不意味着它没用,当下很火…...

[论文笔记]BiMPM
引言 这又是一篇文本匹配的论文Bilateral Multi-Perspective Matching for Natural Language Sentences阅读笔记。 论文题目为自然语言文本中双向多视角匹配。 提出了BiMPM(bilateral multi-perspective matching)模型: 基于匹配-聚合(比较-聚合)框架; 采用双向匹配提取交…...
JS判断当前是早上,中午,下午还是晚上
<!DOCTYPE html> <html><head><meta charset"utf-8" /><title></title></head><body><div></div><script>function getTimeState() {// 获取当前时间let timeNow new Date();// 获取当前小时let…...

使用Docker部署Gitlab的记录
docker版本 使用docker -v查看 Docker version 1.13.1, build 7d71120/1.13.1运行容器镜像 映射本机的9980端口为Docker内部的80端口 映射本机的9922端口为Docker内部的22端口 使用root用户启动 映射本机目录/mnt/sda/gitlab/log为Docker内部的/var/log/gitlab 映射本机目录…...
Spark【Spark SQL(二)RDD转换DataFrame、Spark SQL读写数据库 】
从 RDD 转换得到 DataFrame Saprk 提供了两种方法来实现从 RDD 转换得到 DataFrame: 利用反射机制推断 RDD 模式使用编程方式定义 RDD 模式 下面使用到的数据 people.txt : Tom, 21 Mike, 25 Andy, 18 1、利用反射机制推断 RDD 模式 在利用反射机制…...
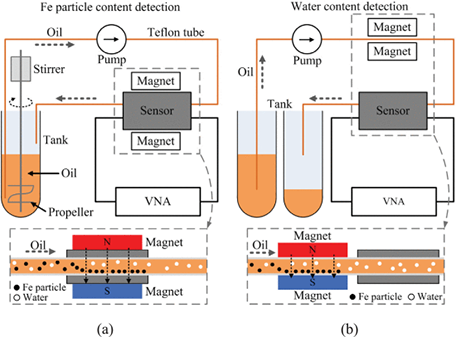
LabVIEW检测润滑油中的水分和铁颗粒
LabVIEW检测润滑油中的水分和铁颗粒 润滑油广泛应用于现代机械设备,由于工作环境日益恶劣,润滑油经常被水分乳化,加速对机械设备的腐蚀。此外,润滑油还受到机械零件摩擦中产生的Fe颗粒的污染,削弱了其机械润滑效果。润…...

【新版】系统架构设计师 - 软件架构设计<SOA与微服务>
个人总结,仅供参考,欢迎加好友一起讨论 架构 - 软件架构设计<SOA与微服务> 考点摘要 面向服务SOA(★★★★)微服务(★★★★) 基于/面向服务的(SOA) 在SO…...
React+Typescript+react-router 6 创建路由操作
本文我们来看看路由的安装 其实路由的操作没有什么变化 但是还是给大家讲一下 那么我们打开项目 在项目终端输入 npm install --save react-router react-router-dom安装 一下 react-router 和 react-router-dom 这都是react开发很基本的插件了 不过大家安装前先注意好我的版…...
前端list.push,封装多个对象
js var fruit [apple, banana];fruit.push(pear);console.log(fruit); // [apple, banana, pear]现在为对象 data1:{addUser: 1,editUser: 1,addTime: null,editTime: 1527410579000,userId: 3,systemNo: mc,userName: zengzhuo,userPassword: e10adc3949ba59abbe56e057f20f88…...

指令延迟隐藏
一、指令延迟隐藏 1. 延迟和延迟隐藏 指令延迟指计算指令从调度到指令完成所需的时钟周期如果在每个时钟周期都有就绪的线程束可以被执行,此时GPU处于满符合状态指令延迟被GPU满负荷计算状态所掩盖的现象称为延迟隐藏延迟隐藏对GPU编程开发很重要,GPU设…...

《React vs. Vue vs. Angular:2023年的全面比较》
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

汇编语言学习(三)——DoxBox中debug的使用
目录 一、安装DoxBox,并下载汇编工具(MASM文件) 二、debug是什么 三、debug中的命令 一、安装DoxBox,并下载汇编工具(MASM文件) 链接: https://pan.baidu.com/s/1IbyJj-JIkl_oMOJmkKiaGQ?pw…...
加密芯片与MCU协同工作的典型流程)
SE(Secure Element)加密芯片与MCU协同工作的典型流程
以下是SE(Secure Element)加密芯片与MCU协同工作的典型流程,综合安全认证、数据保护及防篡改机制: 一、基础认证流程(参数保护方案) 密钥预置 SE芯片与MCU分别预置相同的3DES密钥(Key1、Key2…...
