当前位置： 首页 > news >正文

【代表团坐车】Python 实现-附ChatGPT解析

news 2025/12/11 13:50:21

1.题目

某组织举行会议，来了多个代表团同时到达，接待处只有一辆汽车，可以同时接待多个代表团，为了提高车辆利用率，请帮接待员计算可以坐满车的接待方案，输出方案数量。
约束:
1.一个团只能上一辆车，并且代表团人数(代表团数量小于30，每人代表团人数小于30)小于汽车容量(汽车容量小于100)
2.需要将车辆坐满
输入描述
第一行 代表团人数，英文逗号隔开，代表团数量小于30，每个代表团人数小于30第二行 汽车载客量，汽车容量小于100
输出描述
坐满汽车的方案数量，如果无解输出0

示例1:
输入
5,4,2,3,2,4,9
10
输出 ：4
说明 ：以下几种方式都可以坐满车，[2,3,5]、[2,4,4]、[2,3,5]、[2,4,4]

2.题解

递归法是一种解决问题的常用算法思想，特别适用于问题具有以下一般特征：

  1. 自相似性： 问题可以分解成一个或多个与原问题相似的子问题。这些子问题可以通过递归地调用同一个函数来解决。
  2. 基本情况： 递归算法需要定义一个或多个基本情况，这些情况下可以直接返回结果，而不再继续递归。基本情况通常是问题规模最小或最简单的情况。

递归的一

相关文章：

【代表团坐车】Python 实现-附ChatGPT解析

1.题目 某组织举行会议，来了多个代表团同时到达，接待处只有一辆汽车，可以同时接待多个代表团，为了提高车辆利用率，请帮接待员计算可以坐满车的接待方案，输出方案数量。 约束: 1.一个团只能上一辆车，并且代表团人数(代表团数量小于30，每人代表团人数小于30)小于汽车容量…...

编程日记 2023/9/11 10:01:46

【Java】x-easypdf: 一种简单易用的PDF处理库

引言 在处理和生成PDF文档时，有许多库可供选择。其中，x-easypdf是一种简单易用的PDF处理库，可以帮助开发人员轻松地创建、编辑和操作PDF文档。本文将介绍x-easypdf的基本概念、安装方法、主要功能以及使用示例。 安装x-easypdf 要使用x-ea…...

编程日记 2023/9/11 10:00:45

1 Linux输入子系统

1 Linux输入子系统 https://www.cnblogs.com/beijiqie1104/p/11418082.html Linux input 子系统详解 https://www.cnblogs.com/yikoulinux/p/15208238.html...

编程日记 2023/9/11 9:59:44

Zabbix 利用 Grafana 进行图形展示

安装grafana和插件 配置zabbix数据源 导入模版 查看数据 1.安装grafana wget https://mirrors.tuna.tsinghua.edu.cn/grafana/yum/rpm/Packages/grafana-10.0.0-1.x86_64.rpm [rootrocky8 apps]# yum install grafana-10.0.0-1.x86_64.rpm [rootrocky8 apps]# systemctl sta…...

编程日记 2023/9/11 9:58:43

【LeetCode周赛】LeetCode第362场周赛

LeetCode第362场周赛 与车相交的点判断能否在给定时间到达单元格将石头分散到网格图的最少移动次数 与车相交的点 给你一个下标从 0 开始的二维整数数组 nums 表示汽车停放在数轴上的坐标。对于任意下标 i，nums[i] [starti, endi] ，其中 starti 是第 i…...

编程日记 2023/9/11 9:57:42

Leetcode128. 最长连续序列

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台 给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 题解&#…...

编程日记 2023/9/11 9:56:40

K8S：kubeadm搭建K8S+Harbor 私有仓库

文章目录 一.部署规划1.主机规划2.部署流程 二.kubeadm搭建K8S1.环境准备2.安装docker3. 安装kubeadm，kubelet和kubectl4.部署K8S集群（1）初始化（2）部署网络插件flannel（3）创建 pod 资源 5.部署 …...

编程日记 2023/9/11 9:55:39

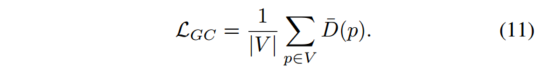
MaskVO: Self-Supervised Visual Odometry with a Learnable Dynamic Mask 论文阅读

论文信息 题目：MaskVO: Self-Supervised Visual Odometry with a Learnable Dynamic Mask 作者：Weihao Xuan, Ruijie Ren, Siyuan Wu, Changhao Chen 时间：2022 来源： IEEE/SICE International Symposium on System Integration …...

编程日记 2023/9/11 9:54:39

面试求职-面试注意事项

面试技巧和注意事项有哪些？ 面试是找工作过程中最重要的一个环节，因为面试成功，你才有可能得到一份工作。求职面试技巧有哪些呢?首先，我们来看看面试注意事项。 企业了解 1、面试前有没有仔细了解过对应企业的情况&#xff0c…...

编程日记 2023/9/11 9:53:36

sm2 签名验签

目前发现 sm2 有很多实现，比如 gmssl, openssl 1.1.1 ,openssl 3.0，各种代码库实现等等。实践中发现这些实现会出现不能互相验签的情况。后续研究一下。 网上的一些资料，给出了一些 openssl 指令，但是没有标明 openssl 的版本&…...

编程日记 2023/9/11 9:52:35

如何检查Windows 11笔记本电脑电池健康状况

如果你拥有一台运行微软最新操作系统的便携式电脑，那么检查Windows 11笔记本电脑的电池健康状况可能很重要。 电池寿命显然是一件大事，无论你是在最好的商务笔记本电脑上工作，还是在目前市场上最好的游戏笔记本电脑上享受马拉松式的Starfiel…...

编程日记 2023/9/11 9:51:34

编程大师-分布式

分布式锁 mysql redis 【IT老齐122】不只setnx，两张图说清Redisson的Redis分布式锁实现_哔哩哔哩_bilibili zk 用这种方式去实现，zookeeper分布式锁，你会吗？_哔哩哔哩_bilibili...

编程日记 2023/9/11 9:50:32

内网隧道代理技术（二十三）之 DNS隧道反弹Shell

DNS隧道反弹Shell DNS隧道 DNS协议是一种请求、应答协议，也是一种可用于应用层的隧道技术。DNS隧道的工作原理很简单，在进行DNS查询时，如果查询的域名不在DNS服务器本机缓存中，就会访问互联网进行查询，然后返回结果。如果在互联网上有一台定制的服务器，那么依靠DNS协议…...

编程日记 2023/9/11 9:49:30

如何利用Socks5代理IP提升网络安全与跨境电商业务

在今天的数字时代，网络安全对于个人和企业来说都至关重要。随着跨境电商和在线游戏等业务的不断发展，保护网络安全变得尤为重要。Socks5代理IP是一项强大的工具，可以帮助您实现更高水平的网络安全，同时促进跨境电商和游戏领域的增…...

编程日记 2023/9/11 9:48:29

信号量（Semaphore）

信号量（Semaphore）是一种经典的多线程同步工具，用于控制多个线程对共享资源的访问。信号量维护了一个计数器，表示可用的资源数量，线程可以通过信号量来请求资源并释放资源。信号量的主要操作包括获取（acquire）资源和释放（release）资源。 Java 中的信号量通常有两种类…...

编程日记 2023/9/11 9:47:28

＜el-input-number＞显示两位数字；如果是一位数字的话前面补0

可以通过自定义 formatter 函数来实现。具体步骤如下&#xff1a; 在 <el-input-number> 上添加 :formatter 属性&#xff0c;值为 formatter 函数名。 在 methods 中定义 formatter 函数&#xff0c;该函数接收一个参数 value&#xff0c;表示当前输入框中的值。 在 f…...

编程日记 2023/9/11 9:46:27

基于SSM的鲜花商城系统【附源码文档】

基于SSM的鲜花商城系统【附源码文档】 开发语言&#xff1a;Java数据库&#xff1a;MySQL技术&#xff1a;SpringSpringMVCMyBatis工具&#xff1a;IDEA/Ecilpse、Navicat、Maven 【主要功能】 角色&#xff1a;用户、管理员 用户&#xff1a;登录、注册、商品查询、公告预…...

编程日记 2023/9/11 9:45:26

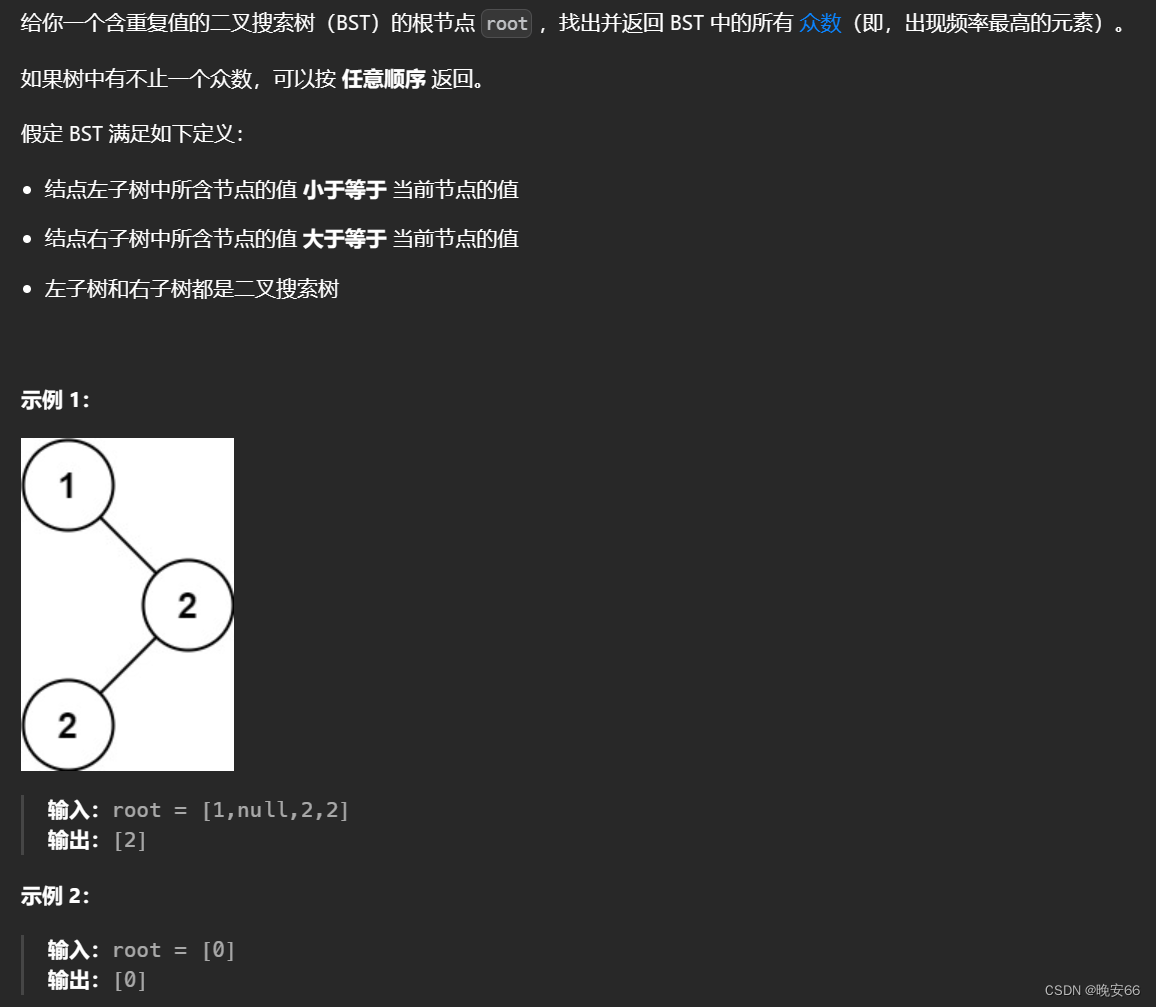
【算法与数据结构】501、LeetCode二叉搜索树中的众数

文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引&#xff0c;可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析&#xff1a;根据前面几篇文章98、LeetCode验证二叉搜索树、530、LeetCode二叉搜索树的最小绝对差。我们知道二叉搜…...

编程日记 2023/9/11 9:44:25

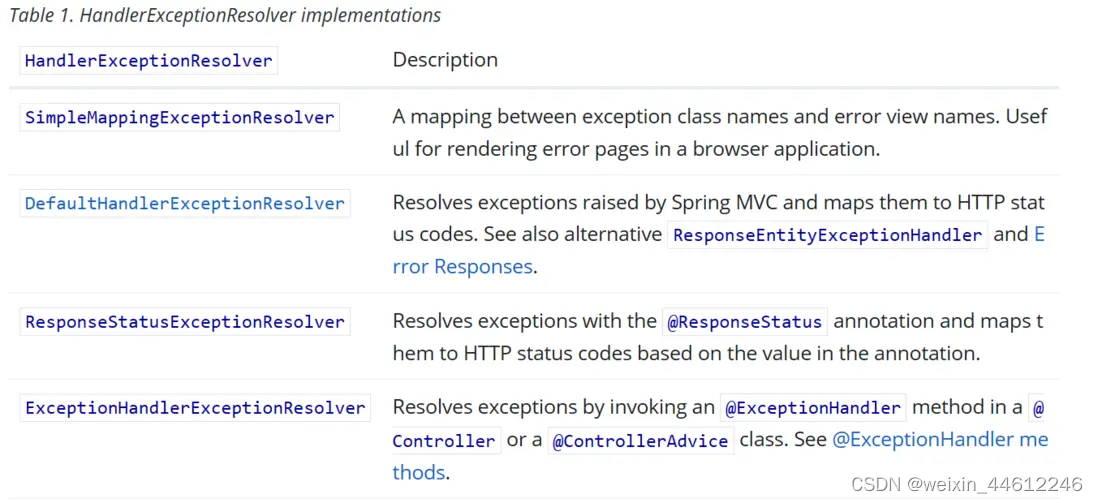
Spring MVC 六 - DispatcherServlet处理请求过程

前面讲过了DispatcherServlet的初始化过程&#xff08;源码角度的DispatcherServlet的具体初始化过程还没说&#xff0c;先放一放&#xff09;&#xff0c;今天说一下DispatcherServlet处理请求的过程。 处理过程 WebApplicationContext绑定在当前request属性上&#xff08;属…...

编程日记 2023/9/11 9:43:24

Python实现猎人猎物优化算法(HPO)优化BP神经网络回归模型(BP神经网络回归算法)项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档视频讲解&#xff09;&#xff0c;如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 猎人猎物优化搜索算法(Hunter–prey optimizer, HPO)是由Naruei& Keynia于2022年提出的一种最新的…...

编程日记 2023/9/11 9:42:23

【Java学习笔记】Arrays类

Arrays 类 1. 导入包&#xff1a;import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序&#xff08;自然排序和定制排序&#xff09;Arrays.binarySearch()通过二分搜索法进行查找&#xff08;前提&#xff1a;数组是…...

编程新知 2025/12/3 9:38:15

STM32+rt-thread判断是否联网

一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

编程新知 2025/9/23 20:06:08

蓝牙 BLE 扫描面试题大全(2)：进阶面试题与实战演练

前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1)&#xff1a;从基础到实战的深度解析-CSDN博客&#xff0c;但实际面试中&#xff0c;企业更关注候选人对复杂场景的应对能力&#xff08;如多设备并发扫描、低功耗与高发现率的平衡&#xff09;和前沿技术的…...

编程新知 2025/12/8 15:08:44

Golang dig框架与GraphQL的完美结合

将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用&#xff0c;可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器&#xff0c;能够帮助开发者更好地管理复杂的依赖关系&#xff0c;而 GraphQL 则是一种用于 API 的查询语言&#xff0c;能够提…...

编程新知 2025/9/30 16:13:37

【算法训练营Day07】字符串part1

文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接&#xff1a;344. 反转字符串 双指针法&#xff0c;两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

编程新知 2025/8/27 14:38:58

Nginx server_name 配置说明

Nginx 是一个高性能的反向代理和负载均衡服务器&#xff0c;其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机&#xff08;Virtual Host&#xff09;。 1. 简介 Nginx 使用 server_name 指令来确定…...

编程新知 2025/9/6 16:47:17

令牌桶 滑动窗口-＞限流 分布式信号量-＞限并发的原理 lua脚本分析介绍

文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结&#xff1a; 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析&#xff1a; 实际业务去理解体会统一注…...

编程新知 2025/12/9 4:34:33

是否存在路径（FIFOBB算法）

题目描述 一个具有 n 个顶点e条边的无向图&#xff0c;该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序&#xff0c;确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数&#xff0c;分别表示n 和 e 的值&#xff08;1…...

编程新知 2025/10/1 6:09:21

Go 语言并发编程基础：无缓冲与有缓冲通道

在上一章节中&#xff0c;我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道&#xff0c;它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好&#xff0…...

编程新知 2025/9/13 17:45:05

【无标题】路径问题的革命性重构：基于二维拓扑收缩色动力学模型的零点隧穿理论

路径问题的革命性重构&#xff1a;基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中&#xff08;图1&#xff09;&#xff1a; mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

编程新知 2025/10/21 1:07:59