【LeetCode周赛】LeetCode第362场周赛
LeetCode第362场周赛
- 与车相交的点
- 判断能否在给定时间到达单元格
- 将石头分散到网格图的最少移动次数
与车相交的点
给你一个下标从 0 开始的二维整数数组 nums 表示汽车停放在数轴上的坐标。对于任意下标 i,nums[i] = [starti, endi] ,其中 starti 是第 i 辆车的起点,endi 是第 i 辆车的终点。
返回数轴上被车 任意部分 覆盖的整数点的数目。
示例 1:
输入:nums = [[3,6],[1,5],[4,7]]
输出:7
解释:从 1 到 7 的所有点都至少与一辆车相交,因此答案为 7 。
示例 2:
输入:nums = [[1,3],[5,8]]
输出:7
解释:1、2、3、5、6、7、8 共计 7 个点满足至少与一辆车相交,因此答案为7 。
提示:
1 < = n u m s . l e n g t h < = 100 1 <= nums.length <= 100 1<=nums.length<=100
n u m s [ i ] . l e n g t h = = 2 nums[i].length == 2 nums[i].length==2
1 < = s t a r t i < = e n d i < = 100 1 <= starti <= endi <= 100 1<=starti<=endi<=100
分析:
这是一个简单的差分数组题,可以用差分数组求出每一个点被覆盖了多少次,答案就是覆盖次数大于0的点的个数。
代码:
class Solution {
public:int numberOfPoints(vector<vector<int>>& nums) {int a[105];memset(a,0,sizeof(a));for(auto num:nums){a[num[0]]++;a[num[1]+1]--;}int ans=0;for(int i=1;i<=100;i++)a[i]+=a[i-1];for(int i=1;i<=100;i++){if(a[i]>0)ans++;}return ans;}
};
判断能否在给定时间到达单元格
给你四个整数 sx、sy、fx、fy 以及一个 非负整数 t 。
在一个无限的二维网格中,你从单元格 (sx, sy) 开始出发。每一秒,你 必须 移动到任一与之前所处单元格相邻的单元格中。
如果你能在 恰好 t 秒 后到达单元格 (fx, fy) ,返回 true ;否则,返回 false 。
单元格的 相邻单元格 是指该单元格周围与其至少共享一个角的 8 个单元格。你可以多次访问同一个单元格。
示例 1:

输入:sx = 2, sy = 4, fx = 7, fy = 7, t = 6
输出:true
解释:从单元格 (2, 4)开始出发,穿过上图标注的单元格,可以在恰好 6 秒后到达单元格 (7, 7) 。
示例 2:

输入:sx = 3, sy = 1, fx = 7, fy = 3, t = 3
输出:false
解释:从单元格 (3, 1)开始出发,穿过上图标注的单元格,至少需要 4 秒后到达单元格 (7, 3) 。 因此,无法在 3 秒后到达单元格 (7, 3)。
提示:
1 < = s x , s y , f x , f y < = 1 0 9 1 <= sx, sy, fx, fy <= 10^9 1<=sx,sy,fx,fy<=109
0 < = t < = 1 0 9 0 <= t <= 10^9 0<=t<=109
分析:
这个题目有一点小坑点,首先,由于可以往八个方向走,因此,最少最少可以用 m a x ( a b s ( s x − f x ) , a b s ( s y − f y ) ) max(abs(sx-fx),abs(sy-fy)) max(abs(sx−fx),abs(sy−fy))步,可以到达指定位置,所以只要t大于等于这个最少步骤,即可满足条件(因为你可以在终点附近一直绕,当绕到相应要求是再去终点即可)。
但是有一个特殊情况,如果起点和终点重合, t = 1 t=1 t=1时,是肯定到不了终点的,因为必须走出去一步,考虑到这一点即可。
代码:
class Solution {
public:bool isReachableAtTime(int sx, int sy, int fx, int fy, int t) {if(sx==fx&&sy==fy){return t!=1;}int minn=max(abs(sx-fx),abs(sy-fy));return t>=minn;}
};
将石头分散到网格图的最少移动次数
给你一个大小为 3 * 3 ,下标从 0 开始的二维整数矩阵 grid ,分别表示每一个格子里石头的数目。网格图中总共恰好有 9 个石头,一个格子里可能会有 多个 石头。
每一次操作中,你可以将一个石头从它当前所在格子移动到一个至少有一条公共边的相邻格子。
请你返回每个格子恰好有一个石头的 最少移动次数 。
示例 1:

输入:grid = [[1,1,0],[1,1,1],[1,2,1]]
输出:3
解释:让每个格子都有一个石头的一个操作序列为:
1 -将一个石头从格子 (2,1) 移动到 (2,2) 。
2 - 将一个石头从格子 (2,2) 移动到 (1,2) 。
3 - 将一个石头从格子(1,2) 移动到 (0,2) 。 总共需要 3 次操作让每个格子都有一个石头。 让每个格子都有一个石头的最少操作次数为 3 。
示例 2:

输入:grid = [[1,3,0],[1,0,0],[1,0,3]]
输出:4
解释:让每个格子都有一个石头的一个操作序列为:
1 -将一个石头从格子 (0,1) 移动到 (0,2) 。
2 - 将一个石头从格子 (0,1) 移动到 (1,1) 。
3 - 将一个石头从格子(2,2) 移动到 (1,2) 。 4 - 将一个石头从格子 (2,2) 移动到 (2,1) 。 总共需要 4次操作让每个格子都有一个石头。 让每个格子都有一个石头的最少操作次数为 4 。
提示:
g r i d . l e n g t h = = g r i d [ i ] . l e n g t h = = 3 grid.length == grid[i].length == 3 grid.length==grid[i].length==3
0 < = g r i d [ i ] [ j ] < = 9 0 <= grid[i][j] <= 9 0<=grid[i][j]<=9
g r i d 中元素之和为 9 。 grid 中元素之和为 9 。 grid中元素之和为9。
分析:
因为数据范围很小,可以考虑全排列求解。根据题意,可以分析出,只要将所有位置多出来的石头移动到位置石头数为0的地方即可。那么我们可以先存储所有石头多的位置和0石头的位置,对0石头的位置进行全排列,然后依次计算从石头多的位置移动到0石头的位置需要多少步,维护一个最小值即可。
代码:
class Solution {
public:int minimumMoves(vector<vector<int>>& grid) {vector<pair<int,int>>more;//存储多出来的点vector<pair<int,int>>less;//存储少的点,即0点for(int i=0;i<grid.size();i++){for(int j=0;j<grid[i].size();j++){if(grid[i][j]>1){int k=grid[i][j];while(k>1){more.push_back({i,j});k--;}}else if(grid[i][j]==0)less.push_back({i,j});}}//对less全排列,然后计算more和less的距离int ans=1e9;do{int cnt=0;for(int i=0;i<less.size();i++){cnt+=abs(more[i].first-less[i].first)+abs(more[i].second-less[i].second);}ans=min(ans,cnt);}while(next_permutation(less.begin(),less.end()));return ans;}
};
相关文章:

【LeetCode周赛】LeetCode第362场周赛
LeetCode第362场周赛 与车相交的点判断能否在给定时间到达单元格将石头分散到网格图的最少移动次数 与车相交的点 给你一个下标从 0 开始的二维整数数组 nums 表示汽车停放在数轴上的坐标。对于任意下标 i,nums[i] [starti, endi] ,其中 starti 是第 i…...

Leetcode128. 最长连续序列
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 题解&#…...
K8S:kubeadm搭建K8S+Harbor 私有仓库
文章目录 一.部署规划1.主机规划2.部署流程 二.kubeadm搭建K8S1.环境准备2.安装docker3. 安装kubeadm,kubelet和kubectl4.部署K8S集群(1)初始化(2)部署网络插件flannel(3)创建 pod 资源 5.部署 …...
MaskVO: Self-Supervised Visual Odometry with a Learnable Dynamic Mask 论文阅读
论文信息 题目:MaskVO: Self-Supervised Visual Odometry with a Learnable Dynamic Mask 作者:Weihao Xuan, Ruijie Ren, Siyuan Wu, Changhao Chen 时间:2022 来源: IEEE/SICE International Symposium on System Integration …...

面试求职-面试注意事项
面试技巧和注意事项有哪些? 面试是找工作过程中最重要的一个环节,因为面试成功,你才有可能得到一份工作。求职面试技巧有哪些呢?首先,我们来看看面试注意事项。 企业了解 1、面试前有没有仔细了解过对应企业的情况,…...

sm2 签名验签
目前发现 sm2 有很多实现,比如 gmssl, openssl 1.1.1 ,openssl 3.0,各种代码库实现等等。实践中发现这些实现会出现不能互相验签的情况。后续研究一下。 网上的一些资料,给出了一些 openssl 指令,但是没有标明 openssl 的版本&…...
如何检查Windows 11笔记本电脑电池健康状况
如果你拥有一台运行微软最新操作系统的便携式电脑,那么检查Windows 11笔记本电脑的电池健康状况可能很重要。 电池寿命显然是一件大事,无论你是在最好的商务笔记本电脑上工作,还是在目前市场上最好的游戏笔记本电脑上享受马拉松式的Starfiel…...

编程大师-分布式
分布式锁 mysql redis 【IT老齐122】不只setnx,两张图说清Redisson的Redis分布式锁实现_哔哩哔哩_bilibili zk 用这种方式去实现,zookeeper分布式锁,你会吗?_哔哩哔哩_bilibili...

内网隧道代理技术(二十三)之 DNS隧道反弹Shell
DNS隧道反弹Shell DNS隧道 DNS协议是一种请求、应答协议,也是一种可用于应用层的隧道技术。DNS隧道的工作原理很简单,在进行DNS查询时,如果查询的域名不在DNS服务器本机缓存中,就会访问互联网进行查询,然后返回结果。如果在互联网上有一台定制的服务器,那么依靠DNS协议…...

如何利用Socks5代理IP提升网络安全与跨境电商业务
在今天的数字时代,网络安全对于个人和企业来说都至关重要。随着跨境电商和在线游戏等业务的不断发展,保护网络安全变得尤为重要。Socks5代理IP是一项强大的工具,可以帮助您实现更高水平的网络安全,同时促进跨境电商和游戏领域的增…...
)
信号量(Semaphore)
信号量(Semaphore)是一种经典的多线程同步工具,用于控制多个线程对共享资源的访问。信号量维护了一个计数器,表示可用的资源数量,线程可以通过信号量来请求资源并释放资源。信号量的主要操作包括获取(acquire)资源和释放(release)资源。 Java 中的信号量通常有两种类…...

<el-input-number>显示两位数字;如果是一位数字的话前面补0
可以通过自定义 formatter 函数来实现。具体步骤如下: 在 <el-input-number> 上添加 :formatter 属性,值为 formatter 函数名。 在 methods 中定义 formatter 函数,该函数接收一个参数 value,表示当前输入框中的值。 在 f…...

基于SSM的鲜花商城系统【附源码文档】
基于SSM的鲜花商城系统【附源码文档】 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatis工具:IDEA/Ecilpse、Navicat、Maven 【主要功能】 角色:用户、管理员 用户:登录、注册、商品查询、公告预…...
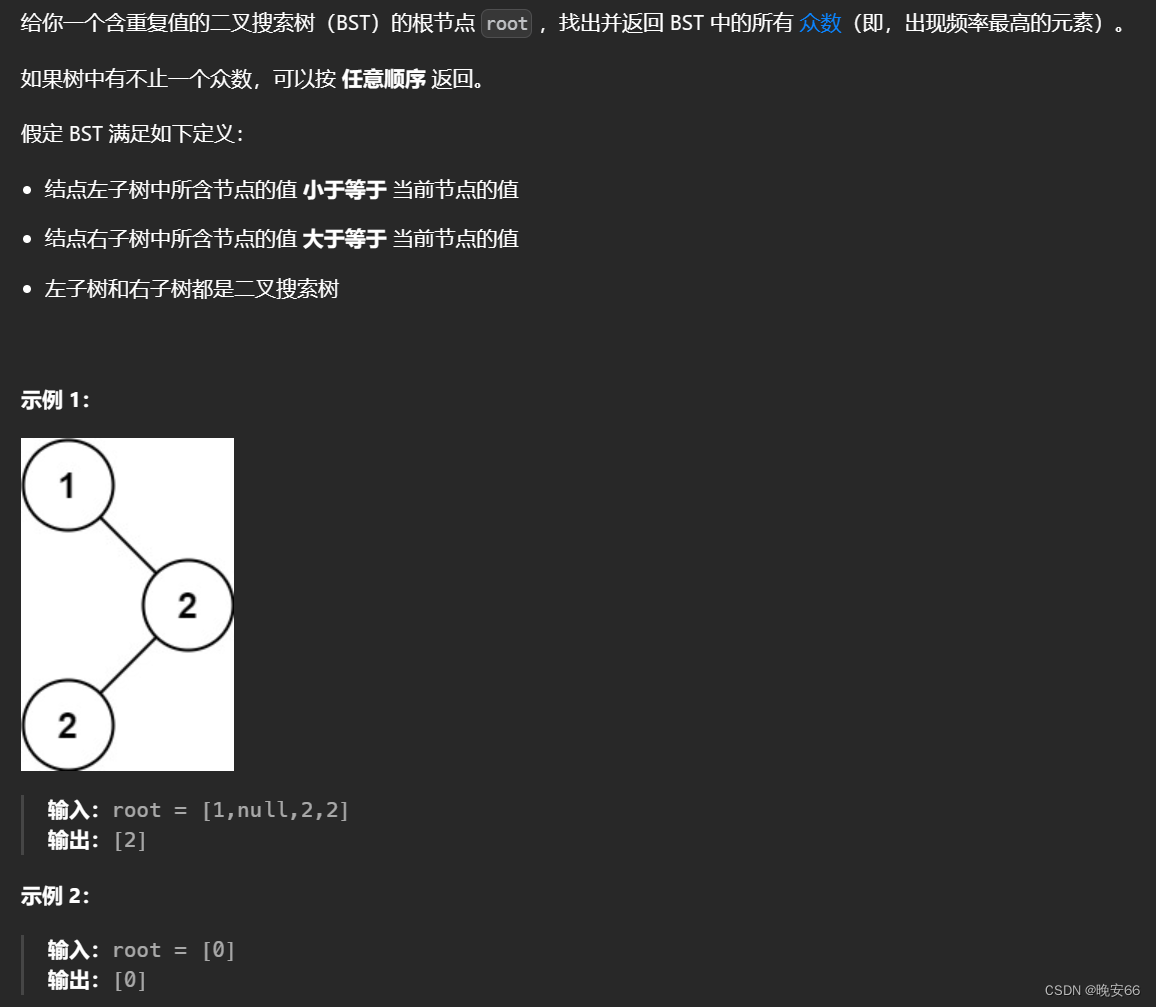
【算法与数据结构】501、LeetCode二叉搜索树中的众数
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:根据前面几篇文章98、LeetCode验证二叉搜索树、530、LeetCode二叉搜索树的最小绝对差。我们知道二叉搜…...
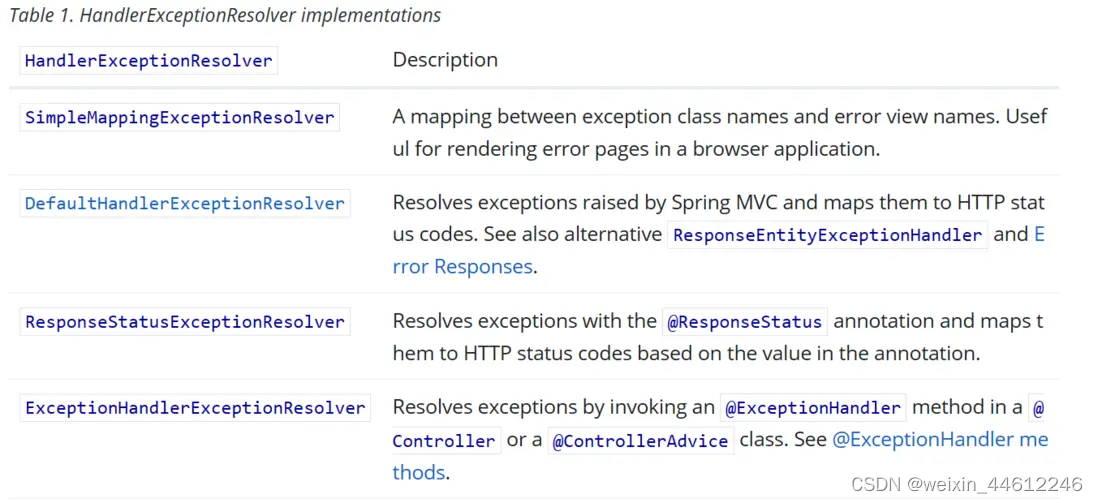
Spring MVC 六 - DispatcherServlet处理请求过程
前面讲过了DispatcherServlet的初始化过程(源码角度的DispatcherServlet的具体初始化过程还没说,先放一放),今天说一下DispatcherServlet处理请求的过程。 处理过程 WebApplicationContext绑定在当前request属性上(属…...

Python实现猎人猎物优化算法(HPO)优化BP神经网络回归模型(BP神经网络回归算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 猎人猎物优化搜索算法(Hunter–prey optimizer, HPO)是由Naruei& Keynia于2022年提出的一种最新的…...

【图论】SPFA求负环
算法提高课笔记 文章目录 基础知识例题虫洞题意思路代码 观光奶牛题意思路代码 单词环题意思路代码 基础知识 负环:环上权值之和是负数 求负环的常用方法 基于SPFA 统计每个点入队次数,如果某个点入队n次,则说明存在负环(完全…...
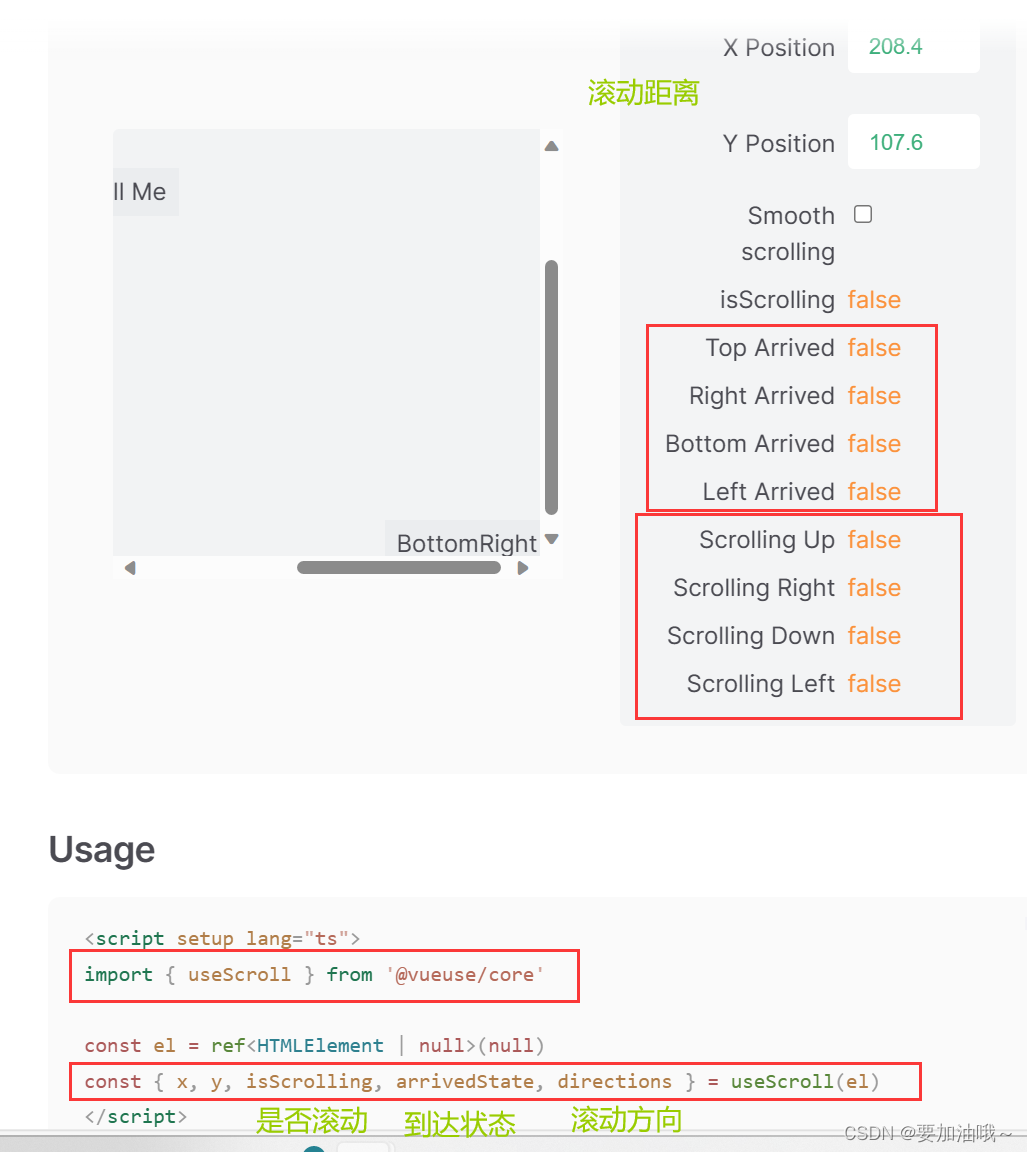
vue3中的吸顶导航交互实现 | VueUse插件
目的:浏览器上下滚动时,若距离顶部的滚动距离大于78px,吸顶导航显示,小于78px隐藏。使用vueuse插件中的useScroll方法和动态类名控制进行实现 1. 安装 npm i vueuse/core 2. 获得滚动距离 项目中导入࿰…...

MySql 笔记
数据结构:BTREE 二叉树:顺序增长依次查询效率低 红黑树: 数据多了深度越深,效率自然低了 HASH: 查询条件限制 B-TREE:度(degree)-节段的数据存储个数,叶节点具有 相…...
部署elasticsearch集群
创建es集群 编写一个docker-compose.yaml文件,内容如下 version: 2.2 services:es01:image: elasticsearch:7.12.1container_name: es01environment:- node.namees01- cluster.namees-docker-cluster- discovery.seed_hostses02,es03- cluster.initial_master_nod…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
