第 362 场 LeetCode 周赛题解
A 与车相交的点
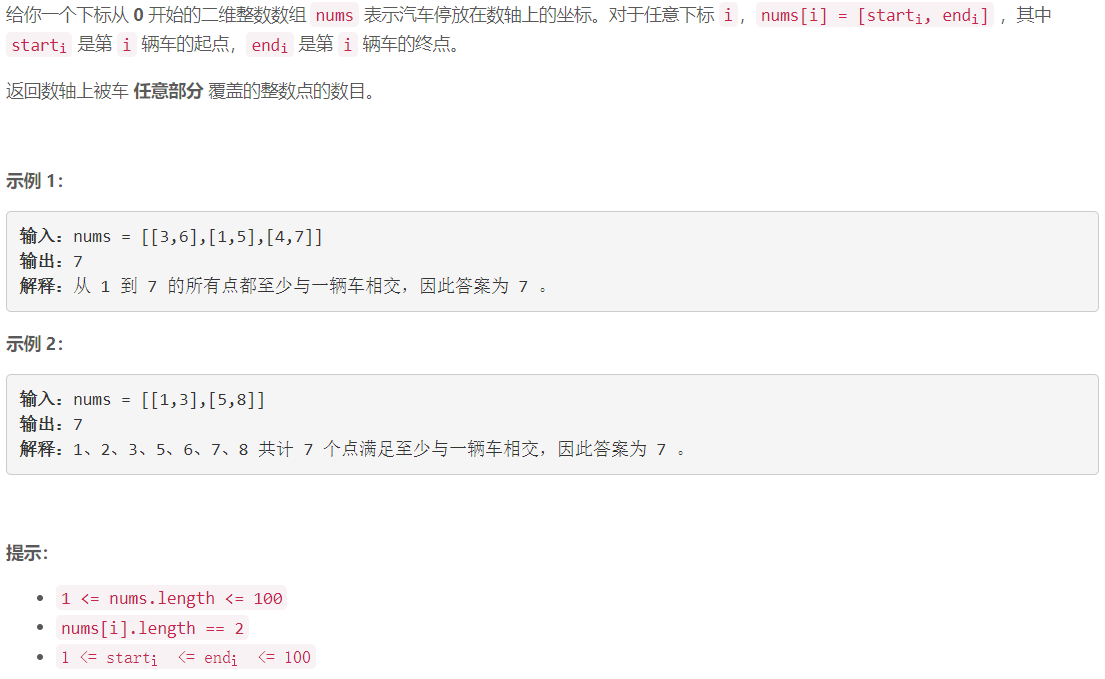
数据范围小直接暴力枚举
class Solution {
public:int numberOfPoints(vector <vector<int>> &nums) {unordered_set<int> vis;for (auto &p: nums)for (int i = p[0]; i <= p[1]; i++)vis.insert(i);return vis.size();}
};
B 判断能否在给定时间到达单元格
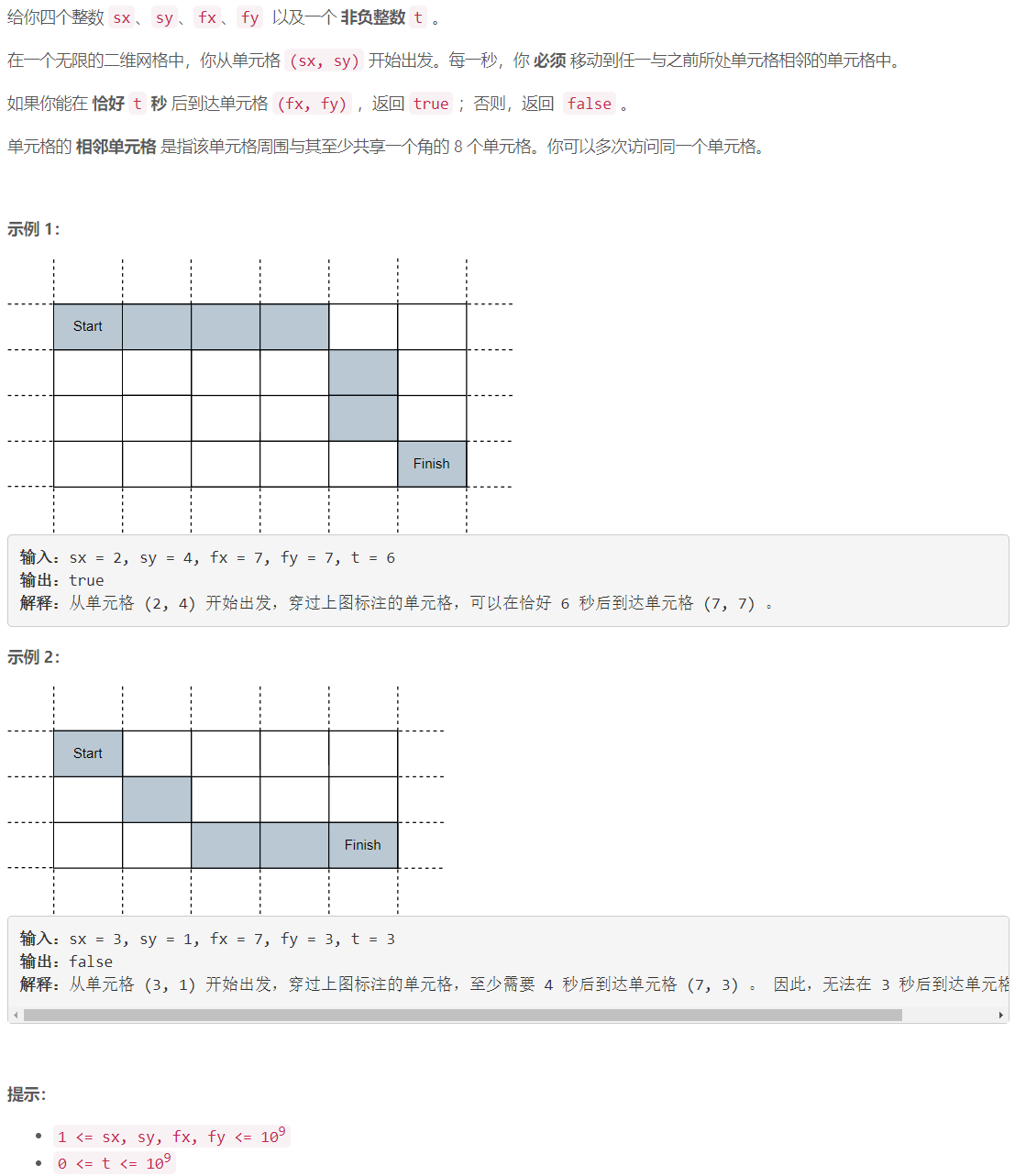
设起点和终点的横坐标之差的绝对值为 d x dx dx , 纵坐标之差的绝对值为 d y dy dy ,则最少需要的时间 m n mn mn 为 m a x ( d x , d y ) max(dx, dy) max(dx,dy),当起点终点不重合时只需要 t ≥ m n t\ge mn t≥mn 即可, 起点终点重合需要 t ≥ 2 t \ge 2 t≥2 或 t = 0 t = 0 t=0。
class Solution {
public:bool isReachableAtTime(int sx, int sy, int fx, int fy, int t) {int dx = abs(sx - fx), dy = abs(sy - fy);int mn = min(dx, dy) + max(dx, dy) - min(dx, dy);if (mn != 0)return t >= mn;return t >= 2|| t == 0;}
};
C 将石头分散到网格图的最少移动次数
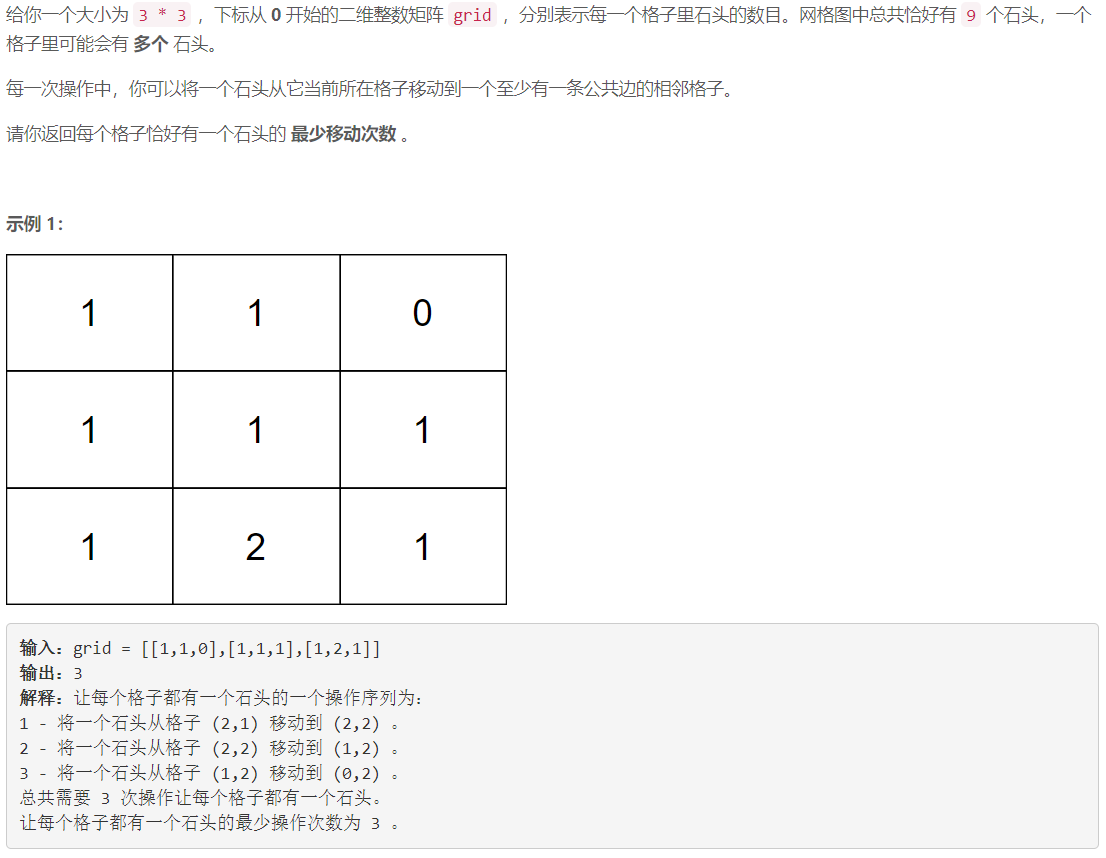
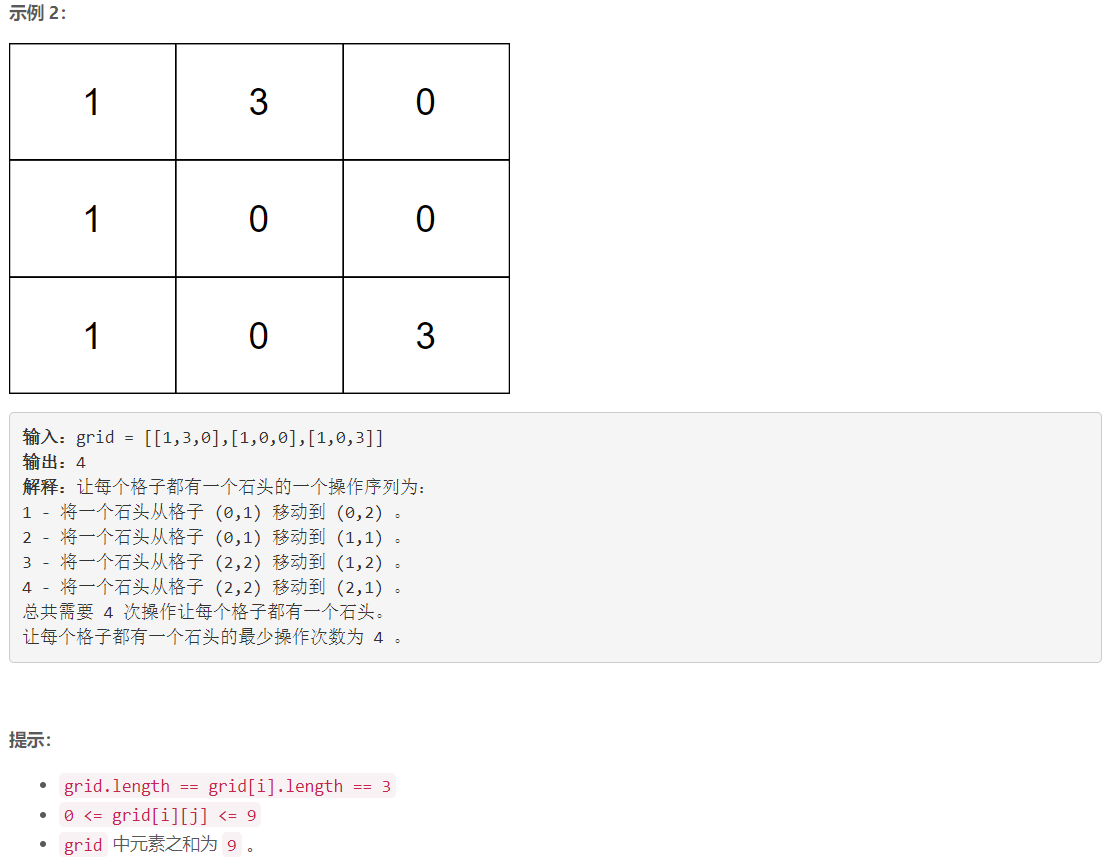
枚举排列:将待移动的石子的坐标加入数组 s t a r t start start ,将没有石子的坐标加入数组 t a r g e t target target ,枚举 s t a r t start start 可能的排列,一种排列和 t a r g e t target target 对应一种移动方案。
class Solution {
public:int minimumMoves(vector<vector<int>> &grid) {vector<pair<int, int>> start, target;for (int i = 0; i < 3; i++)for (int j = 0; j < 3; j++)if (grid[i][j] >= 1) {for (int k = 0; k < grid[i][j] - 1; k++)start.emplace_back(i, j);} else if (grid[i][j] == 0)target.emplace_back(i, j);sort(start.begin(), start.end());int res = INT32_MAX;do {int t = 0;for (int i = 0; i < start.size(); i++) {t += abs(start[i].first - target[i].first) + abs(start[i].second - target[i].second);if (t >= res)break;}res = min(res, t);} while (next_permutation(start.begin(), start.end()));return res;}
};
D 字符串转换

动态规划 + 字符串哈希 + 矩阵快速幂:设 c n t cnt cnt 为满足“将 s s s 的长为 l ( 0 ≤ l < n ) l(0\le l<n) l(0≤l<n) 的后缀移动到 s s s 的开头后 s = = t s==t s==t ” 的 l l l 的个数。设 p k p_k pk 为:恰好 k k k 次操作后 s s s 变为 t t t 的方案数,设 q k q_k qk 为:恰好 k k k 次操作后 s s s 不能变为 t t t 的方案数,因为题目要求操作的后缀长度 0 < l < n 0<l<n 0<l<n , 所以有矩阵形式的转移方程: [ p k q k ] = [ c n t − 1 c n t n − c n t n − c n t − 1 ] [ p k − 1 q k − 1 ] \begin{bmatrix} p_k\\ q_k \end{bmatrix}=\begin{bmatrix} cnt -1 & cnt\\ n-cnt & n-cnt-1 \end{bmatrix} \begin{bmatrix} p_{k-1}\\ q_{k-1} \end{bmatrix} [pkqk]=[cnt−1n−cntcntn−cnt−1][pk−1qk−1]
若 s = = t s==t s==t 则 [ p 0 , q 0 ] T = [ 1 , 0 ] T [p_0,q_0]^T=[1,0]^T [p0,q0]T=[1,0]T ,否则 [ p 0 , q 0 ] T = [ 0 , 1 ] T [p_0,q_0]^T=[0,1]^T [p0,q0]T=[0,1]T,设转移方程中的方阵为 A A A ,则有 [ p k , q k ] T = A k [ p 0 , q 0 ] T [p_k,q_k]^T=A^k[p_0,q_0]^T [pk,qk]T=Ak[p0,q0]T ,通过矩阵快速幂求 A k A^k Ak 。
class Solution {
public:using ll = long long;using type_mat = vector<vector<ll>>;ll mod = 1e9 + 7;type_mat pow_mat(type_mat &mat, ll n) {//矩阵快速幂type_mat res = mat;//mat^n=mat*mat^(n-1)n--;for (type_mat e = mat; n; e = mat_product(e, e), n >>= 1)if (n & 1)res = mat_product(res, e);return res;}vector<vector<ll>> mat_product(type_mat &a, type_mat &b) {//矩阵乘法int m = a.size(), n = b[0].size(), mid = a[0].size();type_mat res(m, vector<ll>(n));for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)for (int k = 0; k < mid; k++)res[i][j] = (res[i][j] + a[i][k] * b[k][j] % mod) % mod;return res;}int numberOfWays(string s, string t, long long k) {int n = s.size();shash h1(s, 2333, 1e9 + 9), h2(t, 2333, 1e9 + 9);int cnt = 0;bool flag = false;//s是否等于tif (h1(0, n - 1) == h2(0, n - 1)) {cnt++;flag = true;}for (int i = 1; i < n; i++)//判断将s长为i的后缀移至s的开头后s是否等于tif (h1(n - i, n - 1) == h2(0, i - 1) && h1(0, n - i - 1) == h2(i, n - 1))cnt++;vector<vector<ll>> A{{cnt - 1, cnt},{n - cnt, n - cnt - 1}};type_mat res = pow_mat(A, k);return flag ? (res[0][0] + mod) % mod : (res[0][1] + mod) % mod;}class shash {//字符串哈希模板public:vector<ll> pres;vector<ll> epow;ll e, p;shash(string &s, ll e, ll p) {int n = s.size();this->e = e;this->p = p;pres = vector<ll>(n + 1);epow = vector<ll>(n + 1);epow[0] = 1;for (int i = 0; i < n; i++) {pres[i + 1] = (pres[i] * e + s[i]) % p;epow[i + 1] = (epow[i] * e) % p;}}ll operator()(int l, int r) {//返回s[l,r]对应的哈希值ll res = (pres[r + 1] - pres[l] * epow[r - l + 1] % p) % p;return (res + p) % p;}};};
相关文章:

第 362 场 LeetCode 周赛题解
A 与车相交的点 数据范围小直接暴力枚举 class Solution { public:int numberOfPoints(vector <vector<int>> &nums) {unordered_set<int> vis;for (auto &p: nums)for (int i p[0]; i < p[1]; i)vis.insert(i);return vis.size();} };B 判断能否…...
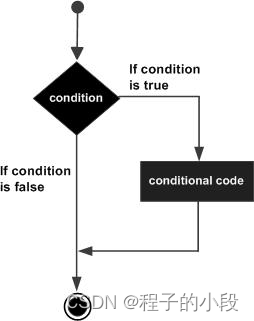
C++ if 语句
一个 if 语句 由一个布尔表达式后跟一个或多个语句组成。 语法 C 中 if 语句的语法: if(boolean_expression) {// 如果布尔表达式为真将执行的语句 }如果布尔表达式为 true,则 if 语句内的代码块将被执行。如果布尔表达式为 false,则 if 语…...
业务安全及实战案例
业务安全 关于漏洞: 注入业务逻辑信息泄露 A04:2021 – Insecure Design 在线靶场PortSwigger 1. 概述 1.1 业务安全现状 1.1.1 业务逻辑漏洞 近年来,随着信息化技术的迅速发展和全球一体化进程的不断加快,计算机和网络已经成为与…...

十一)Stable Diffussion使用教程:人物三视图
现在我们通过一个个具体的案例,去进阶SD的使用。 本篇案例:绘制Q版人物三视图 1)我们先选择一个偏3D的模型,选择文生图,输入魔法; 2)然后选择触发三视图的Lora:<lora:charturnerbetaLora_charturnbetalora:0.6>,注意这里的名称都是本地重新命名的,非原来C站下…...

超级等级福利礼包
文章目录 一、 介绍二、 设计等级礼包的目的1. 提升游戏玩家活跃度2. 提升游戏用户吸引力3. 提高游戏用户留存率4. 实现间接收入5. 持续营收 三、 玩家心理总结四、总结该模式的赢利点五、 该模式的应用场景举例 一、 介绍 超级等级福利礼包,玩家每升级5级即可获得…...

如何用Jmeter提取和引用Token
1.执行获取token接口 在结果树这里,使用$符号提取token值。 $根节点,$.data.token表示提取根节点下的data节点下的token节点的值。 2.使用json提取器,提取token 变量路径就是把在结果树提取的路径写上。 3.使用BeanShell取样器或者BeanShell后…...

C#文件拷贝工具
目录 工具介绍 工具背景 4个文件介绍 CopyTheSpecifiedSuffixFiles.exe.config DataSave.txt 拷贝的存储方式 文件夹介绍 源文件夹 目标文件夹 结果 使用 *.mp4 使用 *.* 重名时坚持拷贝 可能的报错 C#代码如下 Form1.cs Form1.cs设计 APP.config Program.c…...

Redis——Java中的客户端和API
Java客户端 在大多数的业务实现中,我们还是使用编码去操作Redis,对于命令的学习只是知道这些数据库可以做什么操作,以及在后面学习到了Java的API之后知道什么方法对应什么命令即可。 官方推荐的Java的客户端网页链接如下: 爪哇…...
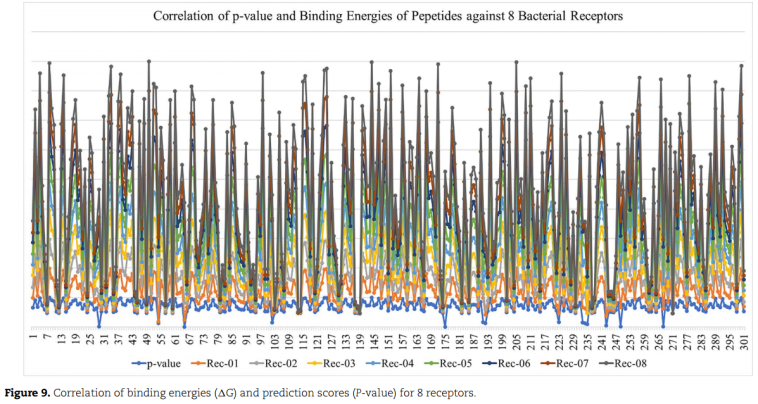
Brief. Bioinformatics2021 | sAMP-PFPDeep+:利用三种不同的序列编码和深度神经网络预测短抗菌肽
文章标题:sAMP-PFPDeep: Improving accuracy of short antimicrobial peptides prediction using three different sequence encodings and deep neural networks 代码:https://github.com/WaqarHusain/sAMP-PFPDeep 一、问题 短抗菌肽(sAMPs)&#x…...

问道管理:华为产业链股再度拉升,捷荣技术6连板,华力创通3日大涨近70%
华为产业链股6日盘中再度拉升,到发稿,捷荣技能涨停斩获6连板,华映科技亦涨停收成3连板,华力创通大涨超19%,蓝箭电子涨约11%,力源信息涨超4%。 捷荣技能盘中再度涨停,近7日已累计大涨超90%。公司…...
面试设计模式-责任链模式
一 责任链模式 1.1 概述 在进行请假申请,财务报销申请,需要走部门领导审批,技术总监审批,大领导审批等判断环节。存在请求方和接收方耦合性太强,代码会比较臃肿,不利于扩展和维护。 1.2 责任链模式 针对…...
Qt 开发 CMake工程
Qt 入门实战教程(目录) 为何要写这篇文章 目前CMake作为C/C工程的构建方式在开源社区已经成为主流。 企业中也是能用CMake的尽量在用。 Windows 环境下的VC工程都是能不用就不用。 但是,这个过程是非常缓慢的,所以࿰…...
2.k8s账号密码登录设置
文章目录 前言一、启动脚本二、配置账号密码登录2.1.在hadoop1,也就是集群主节点2.2.在master的apiserver启动文件添加一行配置2.3 绑定admin2.4 修改recommended.yaml2.5 重启dashboard2.6 登录dashboard 总结 前言 前面已经搭建好了k8s集群,现在设置下…...

【代表团坐车】Python 实现-附ChatGPT解析
1.题目 某组织举行会议,来了多个代表团同时到达,接待处只有一辆汽车,可以同时接待多个代表团,为了提高车辆利用率,请帮接待员计算可以坐满车的接待方案,输出方案数量。 约束: 1.一个团只能上一辆车,并且代表团人数(代表团数量小于30,每人代表团人数小于30)小于汽车容量…...

【Java】x-easypdf: 一种简单易用的PDF处理库
引言 在处理和生成PDF文档时,有许多库可供选择。其中,x-easypdf是一种简单易用的PDF处理库,可以帮助开发人员轻松地创建、编辑和操作PDF文档。本文将介绍x-easypdf的基本概念、安装方法、主要功能以及使用示例。 安装x-easypdf 要使用x-ea…...

1 Linux输入子系统
1 Linux输入子系统 https://www.cnblogs.com/beijiqie1104/p/11418082.html Linux input 子系统详解 https://www.cnblogs.com/yikoulinux/p/15208238.html...
Zabbix 利用 Grafana 进行图形展示
安装grafana和插件 配置zabbix数据源 导入模版 查看数据 1.安装grafana wget https://mirrors.tuna.tsinghua.edu.cn/grafana/yum/rpm/Packages/grafana-10.0.0-1.x86_64.rpm [rootrocky8 apps]# yum install grafana-10.0.0-1.x86_64.rpm [rootrocky8 apps]# systemctl sta…...

【LeetCode周赛】LeetCode第362场周赛
LeetCode第362场周赛 与车相交的点判断能否在给定时间到达单元格将石头分散到网格图的最少移动次数 与车相交的点 给你一个下标从 0 开始的二维整数数组 nums 表示汽车停放在数轴上的坐标。对于任意下标 i,nums[i] [starti, endi] ,其中 starti 是第 i…...

Leetcode128. 最长连续序列
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 题解&#…...
K8S:kubeadm搭建K8S+Harbor 私有仓库
文章目录 一.部署规划1.主机规划2.部署流程 二.kubeadm搭建K8S1.环境准备2.安装docker3. 安装kubeadm,kubelet和kubectl4.部署K8S集群(1)初始化(2)部署网络插件flannel(3)创建 pod 资源 5.部署 …...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...
