地图结构 | 图解占据栅格地图原理(附Matlab建图实验)
目录
- 0 专栏介绍
- 1 栅格地图
- 1.1 应用场景
- 1.2 基本概念
- 2 占据栅格地图
- 2.1 更新模型
- 2.2 截断策略
- 3 仿真实现
- 3.1 算法流程
- 3.2 Matlab实现
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 栅格地图
1.1 应用场景

栅格地图(grid map)是在机器人和自动化领域中广泛使用的一种地图表示方法。它将环境划分为规则的网格单元,并在每个单元中存储关于该区域的信息。每个单元可以表示空闲、障碍物、未知区域或其他地图属性。
栅格地图最主要的应用是服务于机器人导航中的路径规划和避障。机器人可以利用栅格地图中的障碍物信息来规划安全的路径,并避开可能的碰撞或危险区域。同时,栅格地图也是SLAM算法中常用的地图表示方式之一。通过与传感器数据融合,机器人能够同时进行自身位置估计和地图构建。
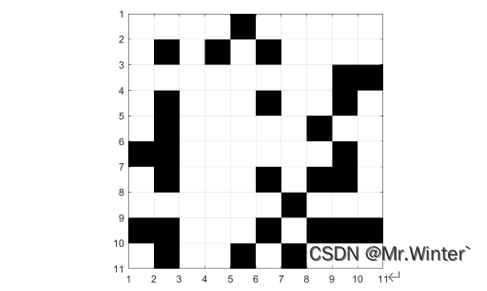
总之,栅格地图是一种简单且直观的地图表示方法,它可以提供对环境的可视化和语义信息,并为机器人的感知、规划和决策提供基础。然而,栅格地图也存在分辨率、存储消耗和精度等方面的限制,在实际应用中需要权衡和优化。
1.2 基本概念
栅格地图的基本概念总结如下
-
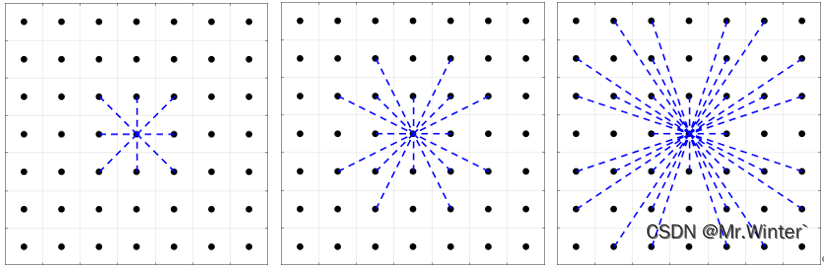
邻域模式
栅格地图中常用的邻域模式有8邻域法、24邻域法和48邻域法,如下所示
-
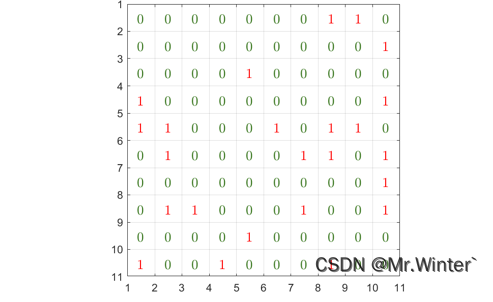
栅格示数
栅格地图中每个栅格都被赋予栅格示数,其指明了该栅格在全局环境中表达的语义。例如0表示无障碍的自由栅格,1表示障碍物
-
栅格坐标
栅格地图可视为离散直角坐标系,其中可用有序二元组 ( i , j ) (i,j) (i,j)定位栅格 -
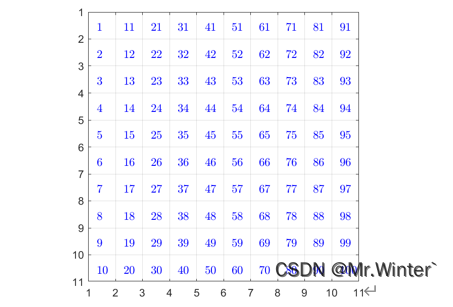
栅格序号
栅格按照行列顺序依次进行的编号称为栅格序号,由于栅格序号是一维线性的,因此可以加速信息处理与运算
-
栅格粒度
栅格对应物理世界的比例系数称为栅格粒度,栅格粒度越小,环境分辨率越大,对环境的刻画越具体、丰富。但相应地,存储地图所占的内存、处理地图耗费的时间越多
2 占据栅格地图
在工程上,通常使用占据法构建占据栅格地图(Occupancy Grid Map)。考虑到构建栅格地图使用的激光雷达存在噪声,即在相同条件下对障碍物的相对距离探测可能有误差,因此引入概率定义栅格状态:对于地图中的栅格 s s s, P ( s = 1 ) P\left( s=1 \right) P(s=1)表示栅格被占据的概率; P ( s = 0 ) = 1 − P ( s = 1 ) P\left( s=0 \right) =1-P\left( s=1 \right) P(s=0)=1−P(s=1)表示栅格自由的概率。实际应用时,使用一种更紧凑的表达
o d d ( s ) = P ( s = 1 ) P ( s = 0 ) \mathrm{odd}\left( s \right) =\frac{P\left( s=1 \right)}{P\left( s=0 \right)} odd(s)=P(s=0)P(s=1)
2.1 更新模型
构建地图的问题可形式化为:已知机器人激光传感器的观测序列 ,更新地图中栅格的后验概率 ,根据贝叶斯公式和马尔科夫链可得
P ( s ∣ z 1 : t ) = P ( z t ∣ s , z 1 : t − 1 ) P ( s ∣ z 1 : t − 1 ) P ( z t ∣ z 1 : t − 1 ) = P ( z t ∣ s ) ⏞ M a r k o v P ( s ∣ z 1 : t − 1 ) P ( z t ∣ z 1 : t − 1 ) = P ( s ∣ z t ) P ( z t ) ⏞ B a y e s P ( s ∣ z 1 : t − 1 ) P ( s ) P ( z t ∣ z 1 : t − 1 ) \begin{aligned}P\left( s|z_{1:t} \right) &=\frac{P\left( z_t|s,z_{1:t-1} \right) P\left( s|z_{1:t-1} \right)}{P\left( z_t|z_{1:t-1} \right)}\\\,\, & =\frac{{ \overset{\mathrm{Markov}}{\overbrace{P\left( z_t|s \right) }}}P\left( s|z_{1:t-1} \right)}{P\left( z_t|z_{1:t-1} \right)}\\&=\frac{{ \overset{\mathrm{Bayes}}{\overbrace{P\left( s|z_t \right) P\left( z_t \right) }}}P\left( s|z_{1:t-1} \right)}{{ P\left( s \right) }P\left( z_t|z_{1:t-1} \right)}\end{aligned} P(s∣z1:t)=P(zt∣z1:t−1)P(zt∣s,z1:t−1)P(s∣z1:t−1)=P(zt∣z1:t−1)P(zt∣s) MarkovP(s∣z1:t−1)=P(s)P(zt∣z1:t−1)P(s∣zt)P(zt) BayesP(s∣z1:t−1)
计算后验概率优势比
P ( s = 1 ∣ z 1 : t ) P ( s = 0 ∣ z 1 : t ) = P ( s = 1 ∣ z t ) P ( s = 0 ∣ z t ) ⋅ P ( s = 1 ∣ z 1 : t − 1 ) P ( s = 0 ∣ z 1 : t − 1 ) ⋅ P ( s = 0 ) P ( s = 1 ) \frac{P\left( s=1|z_{1:t} \right)}{P\left( s=0|z_{1:t} \right)}=\frac{P\left( s=1|z_t \right)}{P\left( s=0|z_t \right)}\cdot \frac{P\left( s=1|z_{1:t-1} \right)}{P\left( s=0|z_{1:t-1} \right)}\cdot \frac{P\left( s=0 \right)}{P\left( s=1 \right)} P(s=0∣z1:t)P(s=1∣z1:t)=P(s=0∣zt)P(s=1∣zt)⋅P(s=0∣z1:t−1)P(s=1∣z1:t−1)⋅P(s=1)P(s=0)
一般令先验概率 P ( s = 0 ) = P ( s = 1 ) = 0.5 P\left( s=0 \right) =P\left( s=1 \right) =0.5 P(s=0)=P(s=1)=0.5,引入Logistic变换
L ( p ) = log [ p / ( 1 − p ) ] L\left( p \right) =\log \left[ {{p}/{\left( 1-p \right)}} \right] L(p)=log[p/(1−p)]
则
L ( s ∣ z 1 : t ) = L ( s ∣ z t ) + L ( s ∣ z 1 : t − 1 ) L\left( s|z_{1:t} \right) =L\left( s|z_t \right) +L\left( s|z_{1:t-1} \right) L(s∣z1:t)=L(s∣zt)+L(s∣z1:t−1)
称为栅格状态的更新模型。更新模型中与新测量值 z t z_t zt有关的项是 L ( s ∣ z t ) L\left( s|z_t \right) L(s∣zt),由于激光雷达的测量值只有两种情况,因此定义
{ l o o c c u : L ( s ∣ z t = 1 ) l o f r e e : L ( s ∣ z t = 0 ) \begin{cases} \mathrm{looccu}: L\left( s|z_t=1 \right)\\ \mathrm{lofree}: L\left( s|z_t=0 \right)\\\end{cases} {looccu:L(s∣zt=1)lofree:L(s∣zt=0)
必须指出, l o o c c u \mathrm{looccu} looccu与 l o f r e e \mathrm{lofree} lofree表达了在获得感知数据的情况下栅格真实状态的概率,这是与传感器性能有关的常数。传感器性能越好,测量结果越接近真实值, l o o c c u \mathrm{looccu} looccu越大 l o f r e e \mathrm{lofree} lofree越小。一般地,可以设定 l o o c c u = 0.9 \mathrm{looccu}=0.9 looccu=0.9、 l o f r e e = − 0.7 \mathrm{lofree}=-0.7 lofree=−0.7
2.2 截断策略
从更新模型可以看出, L ( s ∣ z 1 : t ) L\left( s|z_{1:t} \right) L(s∣z1:t)是对历史观测序列的整合。换言之,若假设 ∣ l o o c c u ∣ = ∣ l o f r e e ∣ \left| \mathrm{looccu} \right|=\left| \mathrm{lofree} \right| ∣looccu∣=∣lofree∣,则当一个栅格被观察到 k k k次自由状态后,必须再被观察到至少 k k k次占据状态,才有可能被设置为占据栅格。这导致实际应用时,动态环境中的地图可能无法被快速更新。
为了建图的适应性,采用截断策略,定义概率上下限来限制改变栅格状态所需的更新次数,代价是概率在0-1区间内不再完备,靠近边界的概率丢失
L ( s ∣ z 1 : t ) = max { min { L ( s ∣ z t ) + L ( s ∣ z 1 : t − 1 ) , L max } , L min } L\left( s|z_{1:t} \right) =\max \left\{ \min \left\{ L\left( s|z_t \right) +L\left( s|z_{1:t-1} \right) , L_{\max} \right\} , L_{\min} \right\} L(s∣z1:t)=max{min{L(s∣zt)+L(s∣z1:t−1),Lmax},Lmin}
3 仿真实现
3.1 算法流程
算法流程如下所示

其中关于Bresenham视线法原理,请参考路径规划 | 图解Theta*算法(附ROS C++/Python/Matlab仿真)
3.2 Matlab实现
核心代码如下所示
for i = 1:N x = scan_pose(1, i);y = scan_pose(2, i);theta = scan_pose(3, i);robot_pos = [ceil(x * resolution) + origin(1), ceil(y * resolution) + origin(2)];% Find grids hit by the rays (in the gird map coordinate)rays = scan_ranges(:, i);x_occ = rays .* cos(scan_angles + theta) + x;y_occ = -rays .* sin(scan_angles + theta) + y;occ_pos = [ceil(x_occ * resolution) + origin(1), ceil(y_occ * resolution) + origin(2)];% Find occupied-measurement cells and free-measurement cellsocc_id = sub2ind(size(grid_map), occ_pos(:, 2), occ_pos(:, 1));free = [];for j = 1:scans_num[ix_free, iy_free] = bresenham(robot_pos, occ_pos(j, :)); free = [free; iy_free, ix_free];endfree_id = sub2ind(size(grid_map), free(:, 1), free(:, 2));% Update the log-oddsgrid_map(occ_id) = grid_map(occ_id) + lo_occ;grid_map(free_id) = grid_map(free_id) - lo_free;% Saturate the log-odd valuesgrid_map(grid_map > lo_max) = lo_max;grid_map(grid_map < lo_min) = lo_min;
end

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

地图结构 | 图解占据栅格地图原理(附Matlab建图实验)
目录 0 专栏介绍1 栅格地图1.1 应用场景1.2 基本概念 2 占据栅格地图2.1 更新模型2.2 截断策略 3 仿真实现3.1 算法流程3.2 Matlab实现 0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索…...
element-plus点击菜单栏全部展开问题解决
这是由子菜单项的index属性引起的,子菜单项的index属性添加相同的值时就会出现这种情况。所以为每个子菜单项添加不同的index属性值就可解决。...

React 简便获取经纬度
以下是关于React获取定位经纬度的代码解释: import React, { useEffect, useState } from react;const LocationComponent () > {const [latitude, setLatitude] useState(null);const [longitude, setLongitude] useState(null);useEffect(() > {navigat…...
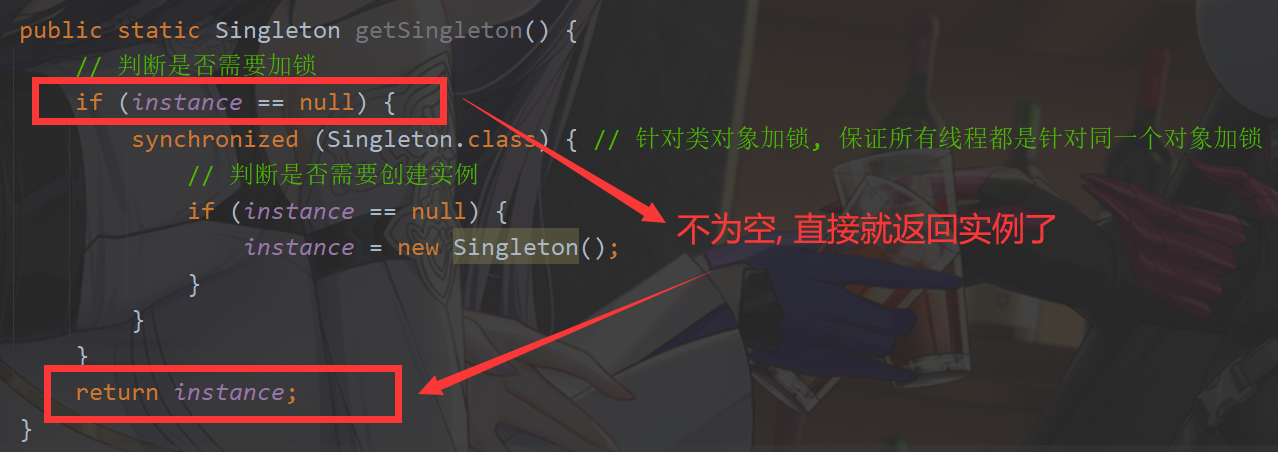
【多线程】线程安全的单例模式
线程安全的单例模式 饿汉模式懒汉模式单线程版多线程版多线程版(改进) 单例模式能保证某个类在程序中只存在 唯一 一份实例, 而不会创建出多个实例,从而节约了资源并实现数据共享。 比如 JDBC 中的 DataSource 实例就只需要一个. 单例模式具体的实现方式, 分成 “饿…...
Competitive Collaboration 论文阅读
论文信息 题目:Competitive Collaboration: Joint Unsupervised Learning of Depth, Camera Motion, Optical Flow and Motion Segmentation 作者:Anurag Ranjan, Varun Jampani, Lukas Balles 来源:CVPR 时间&#x…...
非科班菜鸡算法学习记录 | 代码随想录算法训练营完结!
这俩月终于结束了233333,之后就是反复复习和背八股了吧,然后整整项目春招再投投投,感觉大部分题都有思路了但是做过的题也会没思路,还是要复习 总结 数组: 双指针用的很多,一般一个指向遍历位置࿰…...

C语言实现三字棋
实现以下: 1游戏不退出,继续玩下一把(循环) 2应用多文件的形式完成 test.c. --测试游戏 game.c -游戏函数的实现 game.h -游戏函数的声明 (2)游戏再走的过程中要进行数据的存储,可以使用3*3的二维数组 char bor…...

【LeetCode】35.复杂链表的复制
题目 请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。 示例 1: 输入:head [[7,null],[13,0],[11,4]…...
)
代码大全阅读随笔(五)
数据初始化要点: 数据初始化过程很容易出错,所以请使用本章介绍的方法,来初始化数据,从而避免由于非预期的初始化值而造成的错误。 最小化变量作用域。 使用相同的变量的语句尽可能的集中在一起。 早期绑定会减少灵活性࿰…...

No1.详解【2023年全国大学生数学建模竞赛】C题——蔬菜类商品的自动定价与补货决策(代码 + 详细输出 + 数据集代码 下载)
时间告诉你什么叫衰老,回忆告诉你什么叫幼稚。不要总在过去的回忆里纠缠,昨天的太阳,晒不干今天的衣裳。 🎯作者主页: 追光者♂🔥 🌸个人简介: 💖[1] 计算机专业硕士研究生💖 🌿[2] 2023年城市之星领跑者TOP1(哈尔滨)🌿 🌟[3] 2022年度博客…...

有什么好用的电容笔?apple pencil替代品推荐
近年来,电容笔越来越成为人们日常生活中常见的数码产品之一。电容笔的便捷性得到了消费者的认可。它逐渐取代无纸化书写。那么到底电容笔哪个品牌好呢,电容笔哪一款最好用呢,今天小编给大家总结几款市面好用的电容笔,让我们一起来…...

什么是回调函数?写出一个示例?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 回调函数⭐ 示例⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴趣、刚刚踏入前…...

深度学习在医疗保健领域的应用:从图像识别到疾病预测
文章目录 深度学习在医学影像识别中的应用1. 癌症检测2. 病理学图像分析3. 医学图像分割 深度学习在疾病预测中的应用1. 疾病风险预测2. 疾病诊断辅助3. 药物研发 深度学习在个性化治疗中的应用1. 基因组学分析2. 临床数据集成 深度学习在医疗保健中的挑战和未来数据隐私和安全…...

SpringBoot实现自定义environment中的value加密
environment中的value为什么要加密? 未经过加密的配置文件,密码均是采用明文密码,很容易导致信息泄露。 SpringBoot environment中的value加密代码如下 package com.xxx.core.encryption;import com.google.common.collect.Maps; import lomb…...

celery的用法--任务调度
在Celery中,任务(Task)是执行特定操作的基本单元。任务可以异步执行,可以带有参数,可以返回结果,可以链式调用,还可以设置任务优先级、超时等属性。 1.定义任务: 使用app.task装饰器…...

MyBatis-Plus学习笔记总结
一、查询 构造器分为QueryWrapper和LambdaQueryWrapper 创建实体类User package com.system.mybatisplus.model;import com.baomidou.mybatisplus.annotation.IdType; import com.baomidou.mybatisplus.annotation.TableField; import com.baomidou.mybatisplus.annotation.…...

How Language Model Hallucinations Can Snowball
本文是LLM系列文章,针对《How Language Model Hallucinations Can Snowball》的翻译。 语言模型幻觉是如何产生雪球的 摘要1 引言2 为什么我们期待幻觉像滚雪球一样越滚越大?3 实验4 我们能防止雪球幻觉吗?5 相关工作6 结论局限性 摘要 在实…...
autojs修改顶部标题栏颜色
顶部标题栏的名字是statusBarColor 不是toolbar。难怪我搜索半天搜不到 修改之后变成这样了 代码如下: "ui"; importClass(android.view.View); importClass(android.graphics.Color); ui.statusBarColor(Color.parseColor("#ffffff")); ui.…...
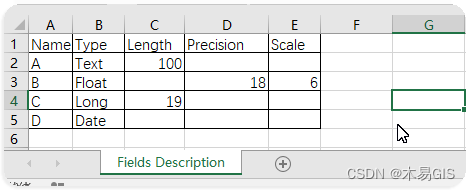
arppy gis 读取text 并批量添加字段 arcpy.AddField_management
arppy gis 读取text 并批量添加字段 arcpy.AddField_management 例:给“省级行政区域”添加“A、B、C、D” 4个字段。 (1)用Excel制作出字段及其描述表,定义字段结构; (2)复制除标题行以为的内…...

Pandas中at、iat函数详解
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 at 函数:通过行名和列名来取值(取行名为a, 列名为A的值) iat 函数:通过行号和列号来取值(取第1行,第1列的值) 本文给出at、iat常见的…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

el-amap-bezier-curve运用及线弧度设置
文章目录 简介示例线弧度属性主要弧度相关属性其他相关样式属性完整示例链接简介 el-amap-bezier-curve 是 Vue-Amap 组件库中的一个组件,用于在 高德地图 上绘制贝塞尔曲线。 基本用法属性path定义曲线的路径,可以是多个弧线段的组合。stroke-weight线条的宽度。stroke…...
