【Hello Algorithm】贪心算法
本篇博客介绍: 简单介绍下贪心算法
贪心算法
- 介绍贪心算法
- 最小字典序的字符串拼接
- 最多会议数
- 切棍子的最小成本
- IPO
- 灯塔问题
介绍贪心算法
贪心算法是一种极具有自然智慧的算法
它会使用以一种局部最功利的标准来做出一个当前看来最好的选择
如果说我们根据局部最优解算出了全局最优解 那么这就是一个有效的贪心
反之我们就可以说 这是一个无效的贪心
(也就是说 我们用贪心算法做题是可能出错的!)
贪心算法的难点在于 我们如何使用局部最功利的标准去得到全局最优解
所以说贪心算法并没有一套很固定的模板 对于贪心算法的学习我们只能是增加阅历和经验为主
下面是贪心算法的反例
现在A要从起点走到终点 再从终点走到起点 从起点到终点的过程中只能够向下或者向左 从终点到起点的过程中智能向上或者向右
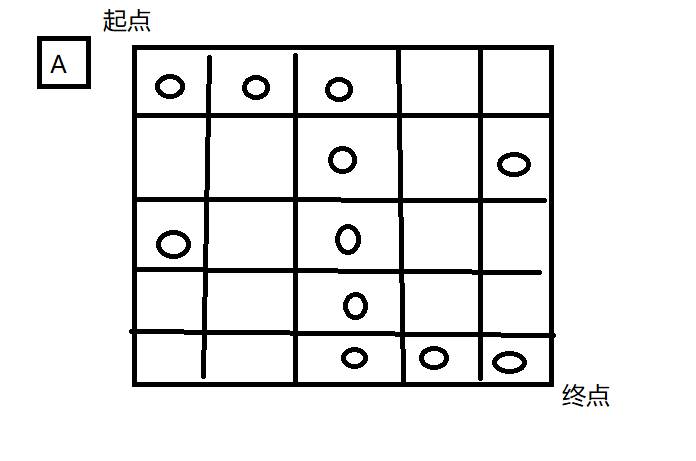
如果我们根据贪心算法来解决 我们的思路是
- 去的时候尽量拿到更多的节点
- 回来的时候尽量拿到更多的节点
我们的路线应该是这样子的

我们可以发现我们少拿了一个节点
但是最佳的路线其实应该是这样子
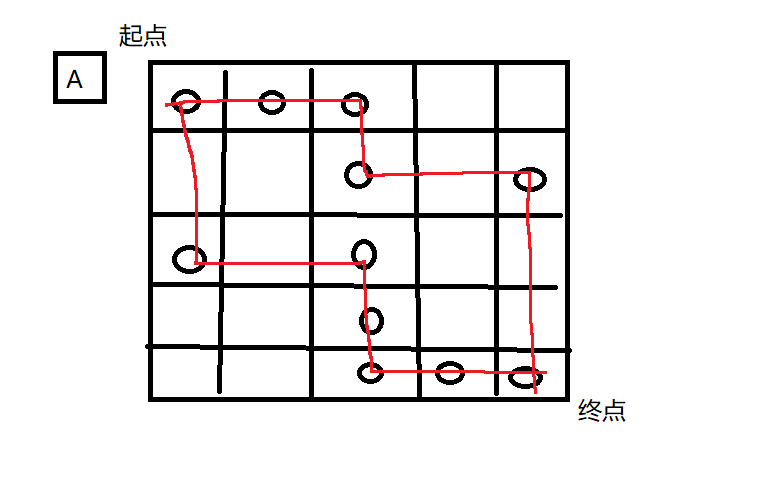
我们全部的节点都拿到了
上面的例子只是为了证明 贪心算法也会出错
最小字典序的字符串拼接
题目如下:
给定我们一个由字符串拼接而成的数组strs 我们必须要把所有的字符串拼接出来 要求我们返回一个字典序最小的拼接结果
首先我们能够确定的是 我们最后拼接出来的字符串长度肯定是一样的
这里同学们一般的贪心策略可能是我们将字符串按照字典序排个序 然后直接拼接起来即可
虽然大部分情况下这种策略是对的 但是也有反例
比如说两个字符串 “b” “ba”
我们明显可以看出 拼接出的最小字符串应该是bab
可以如果按照我们的算法 我们得到的就是字符串bba 明显不对
正确的贪心算法如下
我们按照以下结果排序 如果a拼接上b 小于 b拼接上a 则a在前 反之b在前
使用我们正确的贪心算法就能够得到正确的结果 "bab"了
关于上面贪心的证明过程有点复杂 而且就算知道了如何证明也没有什么意义 其他的题目并不通用 这也就是为什么说学习贪心算法只是为了增加阅历
如果对于这个证明过程有兴趣的同学可以去b站查看左神的算法课学习
这道题我们可以在牛客网上做
最小字典序
代码表示如下
#include <iostream>
using namespace std;
#include <string>
#include <vector>
#include <algorithm>bool Less(const string& s1 , const string& s2){return s1 + s2 < s2 + s1;}int main()
{int count = 0;cin >> count;vector<string> strs;strs.resize(count);int i = 0;string str;while (count--){cin >> str;strs[i] = str;i++;}sort(strs.begin() , strs.end() , Less);string ans;for (int j = 0; j < strs.size() ; j ++){ans += strs[j];}cout << ans << endl;
}
还有就是 一般来说面试的时候不会考查贪心算法
如果考查了 那么我们可以直接跟面试官说 我不确定我的思路对不对 但是我可以使用对数器 一个个来验证我的思路
最多会议数
给你一个数组 events,其中 events[i] = [startDayi, endDayi] ,表示会议 i 开始于 startDayi ,结束于 endDayi 。
你可以在满足 startDayi <= d <= endDayi 中的任意一天 d 参加会议 i 。注意,一天只能参加一个会议。
请你返回你可以参加的 最大 会议数目。
这道题我们贪心的想法可能会有很多 比如说:
- 我们每次排序之后选出时间最早的会议 之后继续排序
- 我们每次选择间隔时间短的会议
- 我们每次都选择结束时间最早的
显然 我们能够提出很多种贪心的方法 但是我们没有办法去一一证明 最快的方式就是直接写出一个暴力方式 然后将上面的几种方案全部写成代码 使用对数器一一对应
对数器能过 那就大概率是对的
我们这里直接给出结论 我们要选择每次开始时间最早的会议
因为我们要尽可能多的参加会议 所以说我们每天的时间最好都是能够用起来的
所以说 我尽量使用date日期来遍历
当然 题目中的隐藏条件就是可以使用的日期等于会议的最后一天 所以说我们也可以利用上这个隐藏条件
我们的整体思路如下
- 首先将所有的会议 按照日期的开始进行排序
- 我们创造一个小根堆 用来存放目前可以被使用的会议
- 如果说当前的日期大于等于会议的开始日期 我们就将所有的会议开始日期进入堆中
- 如果堆中存在可以开的会议我们就开会 如果不存在我们就data++ 直到堆中有数据为止
代码表示如下
class Solution {
public:static bool Less(vector<int>& v1 , vector<int>& v2){return v1[0] < v2[0];}int maxEvents(vector<vector<int>>& events) {sort(events.begin() , events.end() , Less);priority_queue<int , vector<int> , greater<int>> pq;int date = 1;int count = 0;int pointer = 0; while (pq.size() || pointer < events.size()){while (pointer < events.size() && events[pointer][0] <= date){pq.push(events[pointer][1]);pointer++;}if (pq.size()){count++;pq.pop();while(pq.size() && pq.top() == date){pq.pop();}}date++;}return count;}
};
切棍子的最小成本
有一根长度为 n 个单位的木棍,棍上从 0 到 n 标记了若干位置。例如,长度为 6 的棍子可以标记如下:
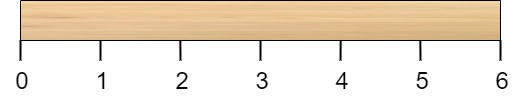
现在我们给定一个数组 数组格式如下 3 2 1 或者 2 2 2 2
总之 该数组的和一定为木棍的长度 现在告诉你 每次切割木棍要花费的代价为木棍的长度 要求怎么样切割花费的代价最小
这道题目的解题代码很简单 但是思路证明很难 还是一样 我们只给出代码思路 对于证明思路有兴趣的同学可以自己去研究
我们数组中所有的数加入到一个小根堆中 设置一个总代价sum
当小根堆的元素大于2的时候 我们每次取出两个元素相加 sum加上这两个元素后 将这两个元素相加后的值再次放进小根堆中
最后我们得到的结果sum就是答案了
IPO
假设 力扣(LeetCode)即将开始 IPO 。为了以更高的价格将股票卖给风险投资公司,力扣 希望在 IPO 之前开展一些项目以增加其资本。 由于资源有限,它只能在 IPO 之前完成最多 k 个不同的项目。帮助 力扣 设计完成最多 k 个不同项目后得到最大总资本的方式。
给你 n 个项目。对于每个项目 i ,它都有一个纯利润 profits[i] ,和启动该项目需要的最小资本 capital[i] 。
最初,你的资本为 w 。当你完成一个项目时,你将获得纯利润,且利润将被添加到你的总资本中。
总而言之,从给定项目中选择 最多 k 个不同项目的列表,以 最大化最终资本 ,并输出最终可获得的最多资本。
这个的贪心我相信大家能够很轻松的想出来 思路如下
- 我们首先找到我们能够参与的项目(需要资金小于等于我们的资金)
- 之后将这些项目按照利润排序 放到一个大堆中
- 之后我们做完一个项目之后更新我们的资金 之后找我们能够参与的项目
- 找到我们能够参与的项目之后 继续放入大堆中 重复上面的操作
这里有一个小细节是 如果我们的初始资金为0 并且没有可以做的项目的话 我们要直接return 0才行
代码表示如下
class Solution {
public:static bool less(const pair<int,int>& kv1 , const pair<int,int>& kv2){return kv1.first < kv2.first; }int findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {vector<pair<int , int>> v;int sum = w;int count = k;int pointer = 0;// 将项目的资金排序for (int i = 0; i < profits.size() ; i++){v.push_back({capital[i] , profits[i]});}sort(v.begin() , v.end() , less);priority_queue<int> pq;while(count--){while(pointer < v.size()){if (v[pointer].first <= sum){pq.push(v[pointer].second);pointer++;}else {break;}}if (pq.empty()){return sum;}sum += pq.top();pq.pop();}return sum;}
};
灯塔问题
有一排灯塔,每个灯塔都有一盏灯,每盏灯可以照亮相邻的两个范围(左边一个和右边一个),但是不能跨过其他灯塔。现在给你一个由字符’X’和’.'组成的字符串,‘X’表示灯塔,’.'表示空地。请你计算最少需要打开多少盏灯,才能让所有的灯塔都被照亮
这也是一个典型的贪心问题
我们的解题思路如下
- 从头开始遍历整个字符串
- 如果遇到了空地 我们不管他
- 如果遇到了灯塔 我们查看灯塔后面的一个元素是什么
- 如果是空地 则我们开灯并且跳跃到空地后一个元素
- 如果是灯塔 那么我们开启后面一个灯塔 并且跳跃着开启灯塔后面的两个位置
代码也很简单 这里就不给出了
总结下 贪心算法并没有一个固定的套路 只能多做 你做过了你就会 你不做你就不会
证明的思路我们不必去一步步验证 对数器能过就说明我们的思路是正确的
相关文章:

【Hello Algorithm】贪心算法
本篇博客介绍: 简单介绍下贪心算法 贪心算法 介绍贪心算法最小字典序的字符串拼接最多会议数切棍子的最小成本IPO灯塔问题 介绍贪心算法 贪心算法是一种极具有自然智慧的算法 它会使用以一种局部最功利的标准来做出一个当前看来最好的选择 如果说我们根据局部最优…...

TOP-K问题
目录 问题描述 解法及思想 第一种方式 算法思想 具体实现 第二种方式 算法思想 具体实现 问题描述 Top-K问题是一个十分经典的问题,一般有以下两种方式来描述问题: 在10亿的数字里,找出其中最大的100个数;在一个包含n个整…...
【保姆级从0到1】UE5 蓝图入门教程1:关卡、蓝图入门
20230113 1、新建项目 新建选择 UE 5.1 项目 选择蓝图,项目位置 改变编辑器布局,选择经典布局 2、关卡与蓝图 选择 File -> New Level 准备创建关卡 选择 Basic,点击 Create 进行创建 Ctrl S 保存新建的关卡 关卡蓝图的打开 鼠标右键&…...

【码银送书第六期】《ChatGPT原理与实战:大型语言模型的算法、技术和私有化》
写在前面 2022年11月30日,ChatGPT模型问世后,立刻在全球范围内掀起了轩然大波。无论AI从业者还是非从业者,都在热议ChatGPT极具冲击力的交互体验和惊人的生成内容。这使得广大群众重新认识到人工智能的潜力和价值。对于AI从业者来说…...

redis 报错 Redis protected-mode 配置文件没有真正启动
(error) DENIED Redis is running in protected mode because protected mode is enabled Redis protected-mode 是3.2 之后加入的新特性,在Redis.conf的注释中,我们可以了解到,他的具体作用和启用条件 链接redis 时只能通过本地localhost …...
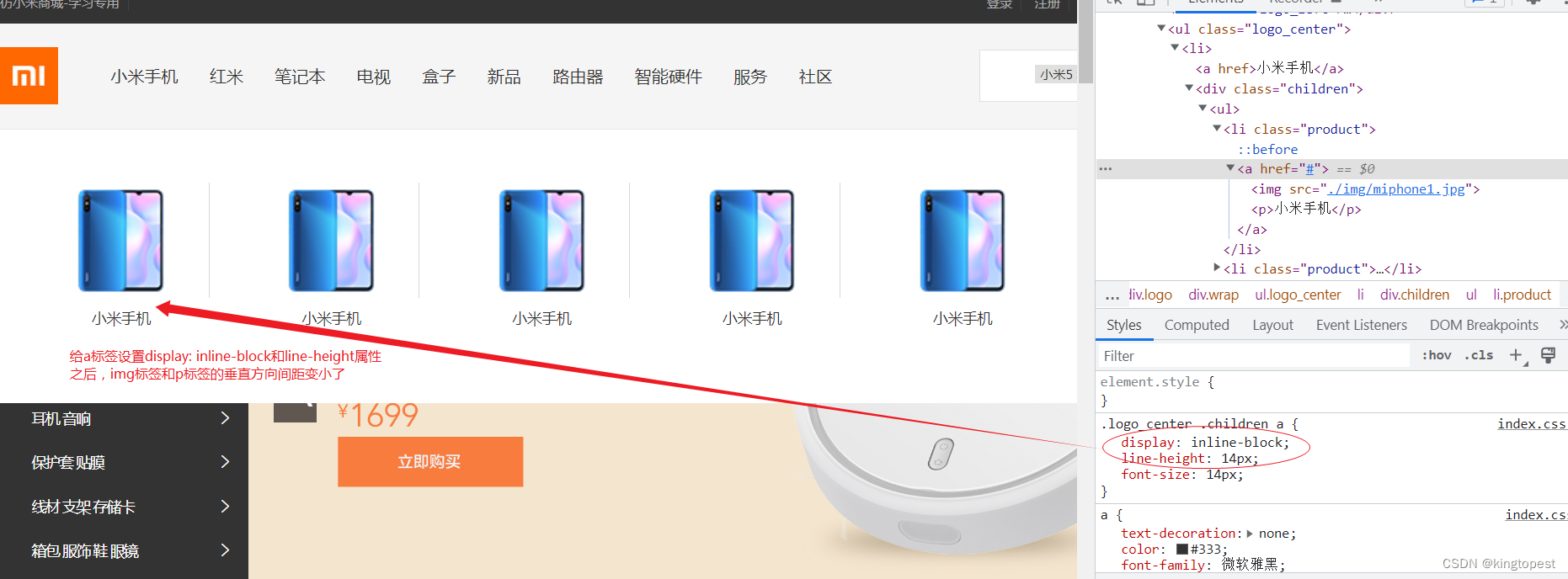
解决a标签内容中img标签和p标签垂直方向间隔太大的问题
现象如下: 对应的html结构: 解决办法:给a标签设置:display: inline-block和line-height属性。 然后问题解决: 具体原理如下(由chatgpt回答): display: inline-block 可以减少垂直方…...

如何选择靠谱的全景平台?VR全景加盟从哪方面对比?
VR全景行业经过近几年的发展,已经逐渐普及开来,线下各个行业都有实体商家开始引入VR全景去做营销宣传推广了。不少老板也意识到线上线下双渠道的重要性,而VR全景的存在就刚好满足各行各业的需求,从这一点不难看出,VR全…...
——CentOS7安装Docker20.10.12和docker compose v2)
CentOS系统环境搭建(十八)——CentOS7安装Docker20.10.12和docker compose v2
centos系统环境搭建专栏🔗点击跳转 CentOS7安装Docker20.10.12和docker compose v2 关于Docker旧版本和docker compose1.0版本的安装可以看这一篇CentOS系统环境搭建(三)——Centos7安装Docker&Docker Compose。 1.卸载旧版本 卸载do…...
NebulaGrap入门介绍和集群安装部署
长风破浪八千里,落日晚霞不回头。 ——大宁。 NebulaGrap——分布式图数据库 官方文档: NebulaGraph Database手册 官方文档 介绍 简介: NebulaGraph 一款开源、分布式图数据库,擅长处理超大规模数据集。 Nebula …...
thinkphp5.0 composer 安装oss提示php版本异常
场景复现: 本地 phpstudy 环境,安装的有7.0到7.3三个版本,首先确认composer已经安装 composer安装阿里云oss的命令为:composer require aliyuncs/oss-sdk-php 运行报错: Problem 1- Root composer.json requires php…...
AList dokcer安装及百度网盘挂载
AList是开源的网盘管理工具。本文介绍如何通过docker安装AList并挂载百度网盘 1、AList安装 1.1、系统安装 通过docker命令进行安装,命令如下: docker run -d --restartalways -v /etc/alist:/opt/alist/data -p 5244:5244 --name"alist" xhofe/alist:…...

whereIn 遇到了最大限制,临时表处理方式
当使用whereIn 遇到了限制,比如whereIn target ID 已经超过了10万级别,但是又没办法join其他库表时,可以使用临时表的方式解决,临时表是以一种会话的方式存在,意味着你断开了mysql 这个临时会话会自动销毁。 为了创建…...
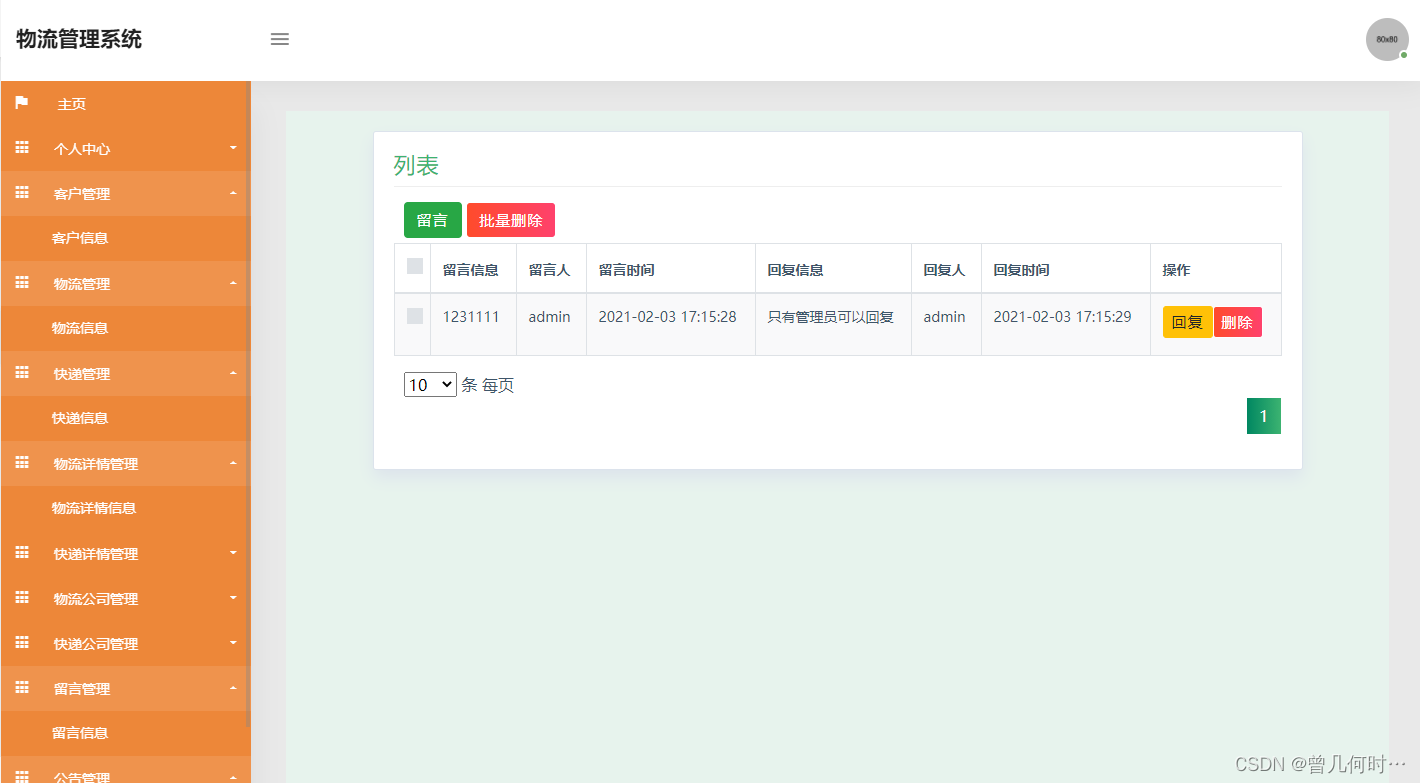
基于SSM的校园快递代取系统设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...
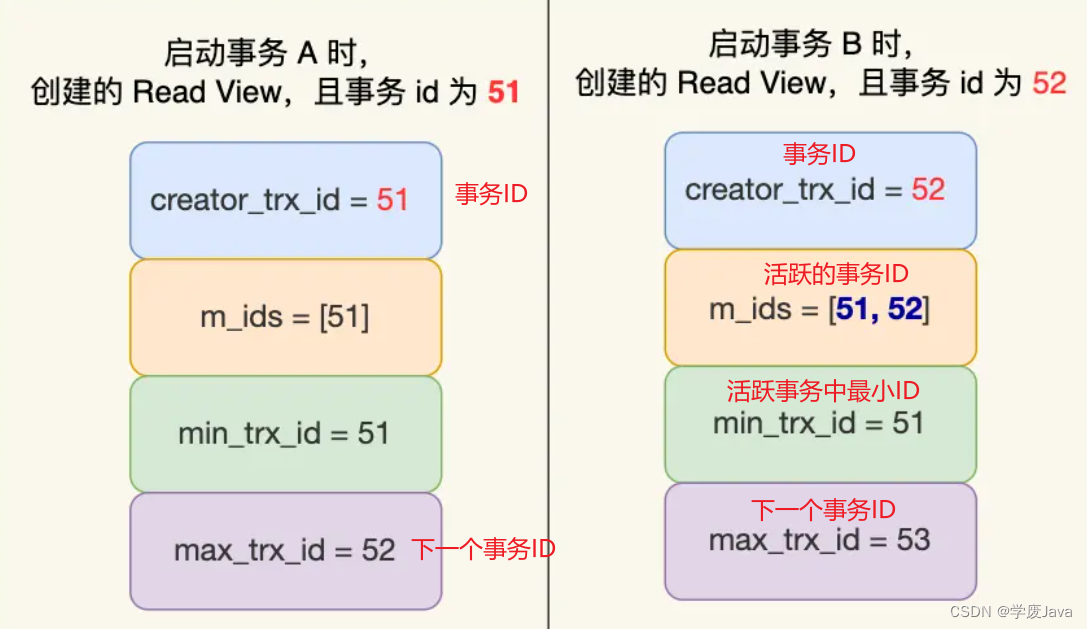
MySQL事务详细讲解
文章目录 什么是事务:1.事务有哪些特性2.并发事务会引起什么问题3.事务的隔离级别有哪些4.Read View在MVCC中如何工作Read View 有四个重要的字段使用 InnoDB 存储引擎的数据库表,它的聚簇索引记录中都包含下面两个隐藏列: 5.可重复读是怎么工作的6.读提…...

[linux] mmcv-full 安装的时候 Building wheel 卡住
(已解决)FileNotFoundError: [Errno 2] No such file or directory: ‘:/usr/local/cuda-11.8/bin/nvcc‘_鳗小鱼的博客-CSDN博客 安装mmcv一直卡在建车轮_梦想成为大佬的王老八的博客-CSDN博客 pip install -U openmim mim install mmcv...

Python怎么实现更高效的数据结构和算法? - 易智编译EaseEditing
要实现更高效的数据结构和算法,你可以考虑以下几个方面的优化: 选择合适的数据结构: 选择最适合你问题的数据结构至关重要。例如,如果需要频繁插入和删除操作,可能链表比数组更合适。如果需要高效查找操作࿰…...

03-zookeeper节点动态上下线案例
服务器动态上下线监听案例 需求 在分布式系统中,主节点可以有多台,可以动态上下线,任意一台客户端都能实时感知到主节点服务器的上下线。 需求分析 客户端能实时洞察到服务器上下线的变化 基本流程: 1.服务端启动时去注册…...

如何使用TensorFlow完成线性回归
线性回归是一种简单的预测模型,它试图通过线性关系来预测目标变量。在TensorFlow中,我们可以使用tf.GradientTape来跟踪我们的模型参数的梯度,然后用这个信息来优化我们的模型参数。 以下是一个简单的线性回归的例子: pythonimpo…...
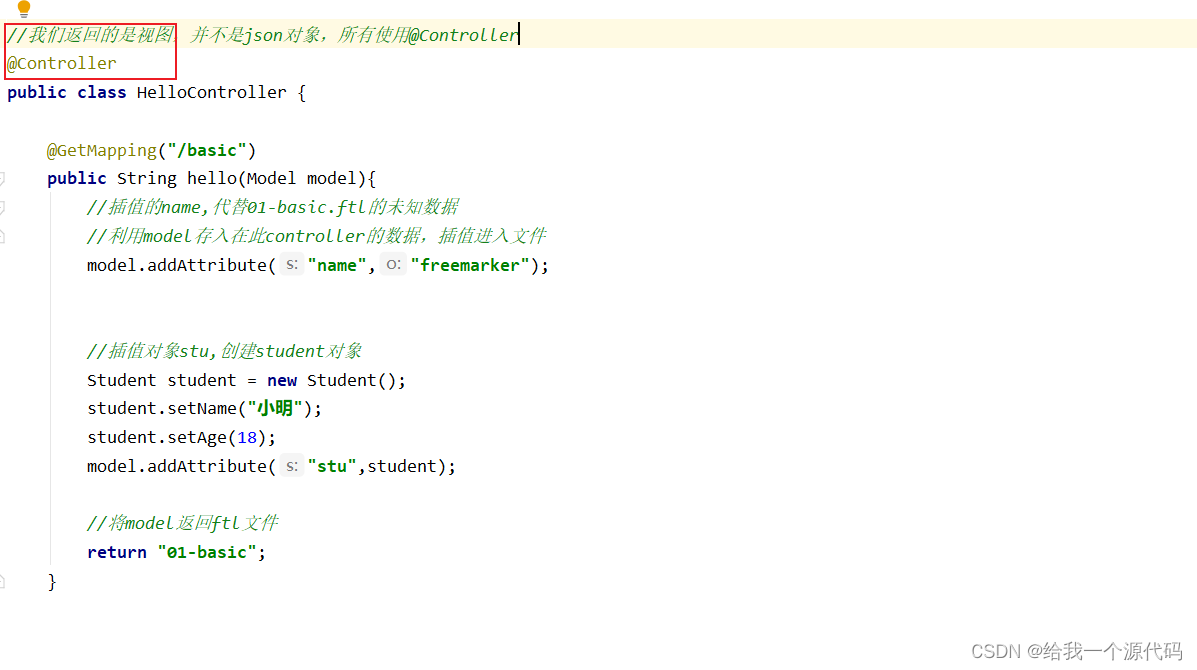
@controller和@RestController的区别
//controller和RestController的区别:RestController的返回值就是结果被输出在浏览器 //controller的返回值会到resources的templates下找 返回值".html" 页面 1.controller 简单的来说,当我们的返回值需要跳转大另一个页面时候,我们就会使…...
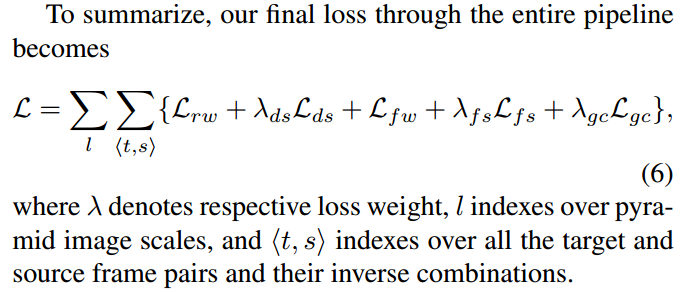
GeoNet: Unsupervised Learning of Dense Depth, Optical Flow and Camera Pose 论文阅读
论文信息 题目:GeoNet: Unsupervised Learning of Dense Depth, Optical Flow and Camera Pose 作者:Zhichao Yin and Jianping Shi 来源:CVPR 时间:2018 Abstract 我们提出了 GeoNet,这是一种联合无监督学习框架&a…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
