数据结构算法刷题(29)动态规划


思路一:回溯:按照选和不选的判断方式,使用回溯来解决这个问题。
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums) #数组的长度
def dfs(i):
if i<0: #到达边界条件后
return 0 #返回最大金额是0
res = max(dfs(i-1),dfs(i-2)+nums[i]) #如果选,下一次递归的就是i-2,并且要加上nums[i]的值,如果不选,下一次递归i-1。比较选或者不选的最大值并返回。
return res
res = dfs(n-1) #传入的是数组的最大下标
return res
问题:回溯使用递归,时间复杂度是指数级别的,会超时,那如何让时间降下来?
思路二:有两次相同的计算结果,那就把每个位置的计算结果保存下来,可以把时间缩短。


class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
cache = [-1]*n #因为每个位置一定不是负数
def dfs(i):
if i<0:
return 0
if cache[i] != -1: #当前的位置不是-1,那么这个位置被计算过,直接返回计算的结果
return cache[i]
res = max(dfs(i-1),dfs(i-2)+nums[i])
cache[i] = res #把当前位置的计算结果保存
return res
res = dfs(n-1)
return res
问题:这种方式的空间复杂度就是O(n),如何将空间复杂度降下来:递推
思路三:我们可以确定的知道每个节点是那几个数归的结果,那把递的过程省略,直接归,也就是从下往上计算结果。


循环对数组下标有要求,所以下标从2开始。
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
f = [0]*(n+2) #归的数组长度是n+2,每个数组的值是0
for i,x in enumerate(nums): #遍历nums
f[i+2] = max(f[i+1],f[i]+x) # 等同于res = max(dfs(i-1),dfs(i-2)+nums[i])
return f[n+1]
改进空间复杂度:

class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
f0 = f1 = 0
for i,x in enumerate(nums):
new_f = max(f1,f0+x)
f0 = f1
f1 = new_f
return f1

思路:

class Solution:
def climbStairs(self, n: int) -> int:
dp0 = 1
dp1 = 1
if n <= 1:
return 1
dp = 0
for i in range(2,n+1):
dp = dp0 + dp1
dp0 = dp1
dp1 = dp
return dp

思路:


class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
n = len(cost)
dp0 = 0 #第0级台阶的顶部最小花费是0
dp1 = min(cost[0],cost[1]) #第1级台阶的顶部台阶的最小花费是cost[0]或cost[1]的最小值
for i in range(2,n):
dp = min(dp1+cost[i],dp0+cost[i-1])
dp0 = dp1
dp1 = dp
return dp1
相关文章:

数据结构算法刷题(29)动态规划
思路一:回溯:按照选和不选的判断方式,使用回溯来解决这个问题。 class Solution: def rob(self, nums: List[int]) -> int: n len(nums) #数组的长度 def dfs(i): if i<0: #到达边界条件后 return 0 #返回最大金额是0 res max(dfs(i…...

W11下CMake MinGW配置OpenCV和Qt
💂 个人主页:风间琉璃🤟 版权: 本文由【风间琉璃】原创、在CSDN首发、需要转载请联系博主💬 如果文章对你有帮助、欢迎关注、点赞、收藏(一键三连)和订阅专栏哦 前言 前几天将cuda版本的opencv给编译成功了,当时用的VS的MSVC&…...

反转字符串 反转字符串 || 反转字符串 |||
思想总结:首先将字符串转变为字符数组,再进行遍历并反转字符。 1.反转字符串 代码: class Solution {public void reverseString(char[] s) {reverse(s,0,s.length); //左闭右开}public static void reverse(char[] ch,int i,int j) { 翻转函…...

XML解析 不允许有匹配 _[xX][mM][lL]_ 的处理指令目标
以上错误是在解析xml参数时候报出的。 我这里错误的原因在于,<?xml version\"1.0\" encoding\"UTF-8\"?>少了个空格,参考下图: 下面一行才是对的。...

【C++进阶(五)】STL大法--list模拟实现以及list和vector的对比
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 list模拟实现 1. 前言2. list类的大致框架与结构…...
Docker安装RabbitMQ集群_亲测成功
先安装Docker Centos7离线安装Docker 华为云arm架构安装Docker RabbitMQ集群模式介绍 RabbitMQ集群搭建和测试总结_亲测 RabbitMQ 有三种模式:单机模式,普通集群模式,镜像集群模式。单机模式即单独运行一个 rabbitmq 实例,而…...

50道基础数据结构面试题
程序员必备的50道数据结构和算法面试题 在本文中,将分享一些常见的编程面试问题,这些问题来自于不同经验水平的程序员,囊括从刚大学毕业的人到具有一到两年经验的程序员。 编码面试主要包括数据结构和基于算法的问题,以及一些诸…...
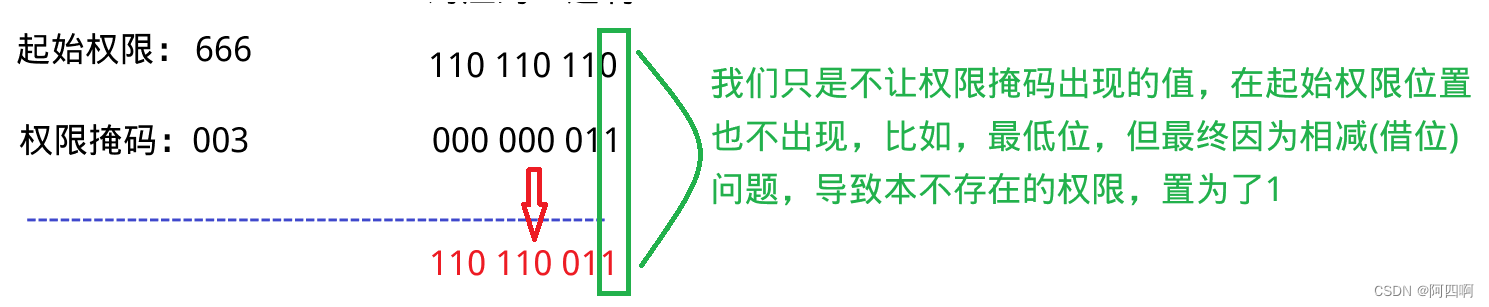
【Linux基础】权限管理
👻内容专栏: Linux操作系统基础 🐨本文概括: 用户之间的切换、sudo提权、Linux权限管理、文件访问权限的相关方法、目录权限、粘滞位等 🐼本文作者: 阿四啊 🐸发布时间:2023.9.11 …...

C++初阶--类和对象(中)
目录 类的6个默认成员函数构造函数使用方法 析构函数使用方法 拷贝构造函数使用方法 赋值运算符重载赋值运算符重载 const成员 上篇末尾我们讲到了关于c实现栈相较于c语言在传递参数时的一些优化,但实际上,c在 初始化 清理 赋值 拷贝等方面也做了很大程…...
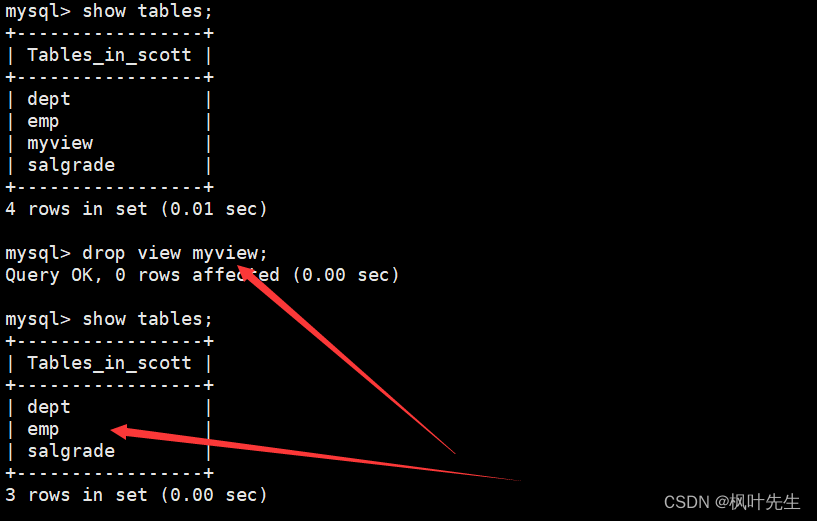
【MySQL系列】视图特性
「前言」文章内容大致是MySQL事务管理。 「归属专栏」MySQL 「主页链接」个人主页 「笔者」枫叶先生(fy) 目录 视图1.1 视图概念1.2 创建视图1.3 修改互相影响1.4 删除视图1.5 视图规则和限制 视图 1.1 视图概念 视图是一个虚拟表,其内容由查询定义同真实的表一样…...

管理类联考——数学——汇总篇——知识点突破——应用题——最值问题
⛲️ 一、考点讲解 最值问题是应用题中最难的题目,也是考生普遍丢分的题目。最值问题一般要结合函数来分析,一般结合二次函数和平均值定理求解。最值问题的求解步骤是:先设未知变量,然后根据题目建立函数表达式,最后利…...

学习SpringMvc第二战之【SpringMVC之综合案例】
目录 一. 参数传递 1.前期准备工作(替换pom.xml中的部分依赖) 1.1将log4j替换成为slf4j(将打印语句替换成为日志文件输出结果) 2.正式操作 1.基础传参 1.1创建方法,用于验证传参 1.2构建界面回显 1.3设置访问路径(localho…...
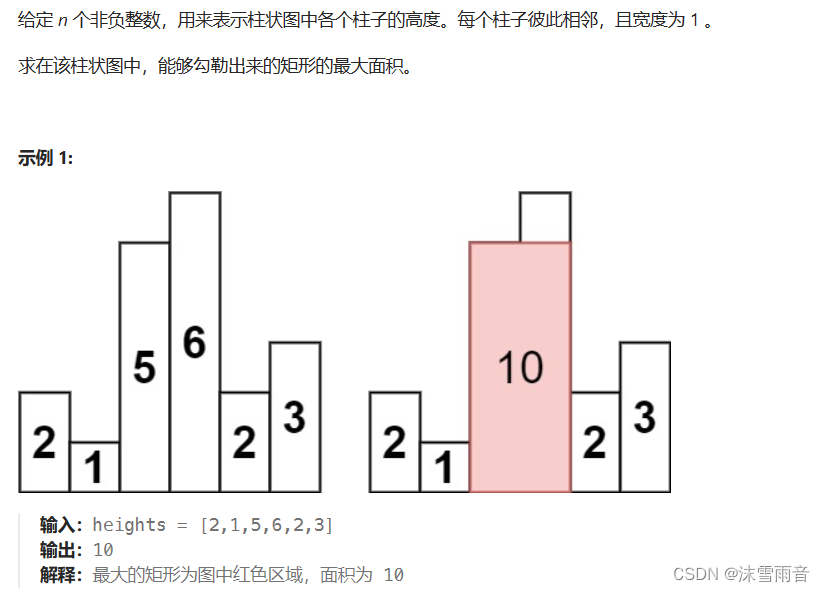
【算法日志】单调栈: 单调栈简介及其应用
代码随想录刷题60Day 目录 单调栈简介 单调栈的应用 下次更高温 下一个更大元素1 下一个更大元素2 接雨水 柱状图中最大矩形 单调栈简介 单调栈(Monotonic Stack)是一种特殊的栈数据结构,它满足元素的单调性,这种单调性需…...
VSCode自动分析代码的插件
今天来给大伙介绍一款非常好用的插件,它能够自动分析代码,并帮你完成代码的编写 效果如下图 首先我们用的是VSCode,(免费随便下) 找到扩展,搜索CodeGeeX,将它下载好,就可以实现了 到…...
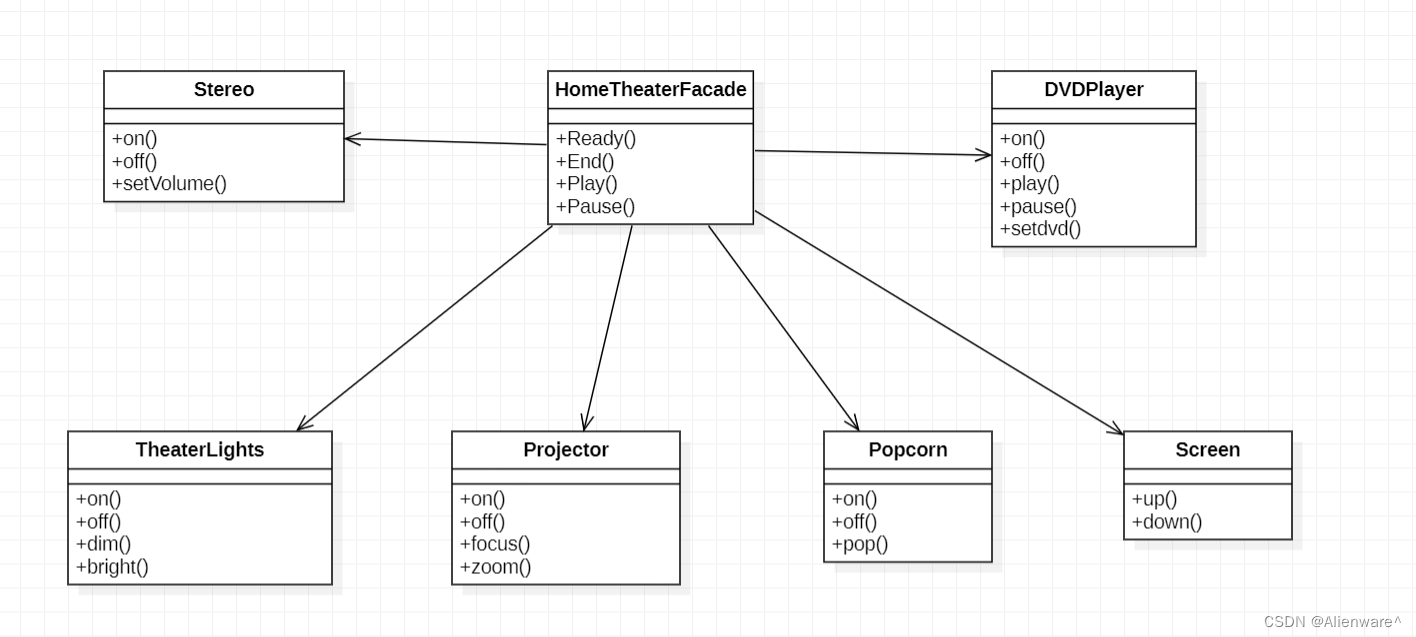
设计模式之外观模式
文章目录 影院管理项目传统方式解决影院管理传统方式解决影院管理问题分析外观模式基本介绍外观模式原理类图外观模式解决影院管理传统方式解决影院管理说明外观模式应用实例 外观模式的注意事项和细节 影院管理项目 组建一个家庭影院: DVD 播放器、投影仪、自动屏…...

Web端测试和 App端测试有何不同?
Web 端测试和 App 端测试是针对不同平台的上的应用进行测试,Web应用和App端的应用实现方式不同,测试时的侧重点也不一样。 今天这篇文章就来介绍下两者的不同之处以及测试时的侧重点。 同时,我也准备了一份软件测试面试视频教程(…...
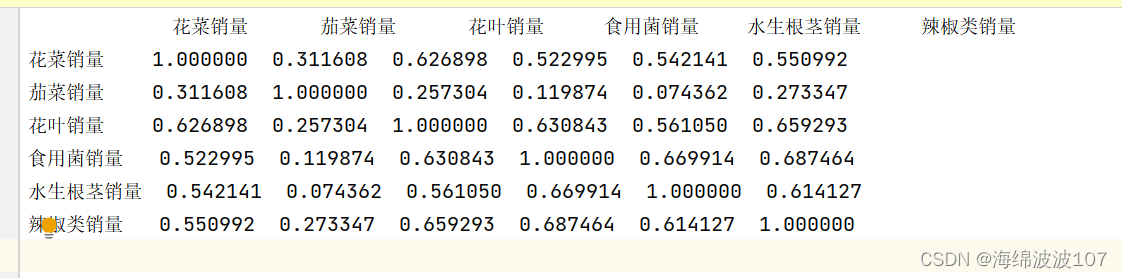
12.(Python数模)(相关性分析一)相关系数矩阵
相关系数矩阵 相关系数矩阵是用于衡量多个变量之间关系强度和方向的统计工具。它是一个对称矩阵,其中每个元素表示对应变量之间的相关系数。 要计算相关系数矩阵,首先需要计算每对变量之间的相关系数。常用的相关系数包括皮尔逊相关系数和斯皮尔曼相关…...

系统架构设计师(第二版)学习笔记----嵌入式系统及软件
【原文链接】系统架构设计师(第二版)学习笔记----嵌入式系统及软件 文章目录 一、嵌入式系统1.1 嵌入式系统的组成1.2 嵌入式系统的特点1.3 嵌入式系统的分类 二、嵌入式软件2.1 嵌入式系统软件分层2.2 嵌入式软件的主要特点 三、安全攸关软件的安全性设…...

Python列表操作指南:索引、切片、遍历与综合应用
文章目录 列表简介创建列表索引和切片列表的长度列表的拼接和重复检查元素是否存在列表的方法index() 方法count() 方法 列表的修改和删除修改元素删除元素列表的排序和反转添加元素 列表的拷贝列表的遍历列表的切片列表的嵌套列表推导式 python精品专栏推荐python基础知识&…...

第15章_锁: MySQL并发访问相同记录以及从数据操作的类型划分锁(读锁、写锁)
事务的 隔离性 由这章讲述的 锁 来实现。 1. 概述 锁是计算机协调多个进程或线程并发访问某一资源的机制. 在程序开发中会存在多线程同步的问题, 当多个线程并发访问某个数据的时候, 尤其是针对一些敏感数据(订单, 金额), 我们就需要保证这个数据在任何时刻最多只有一个线…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
