当前位置： 首页 > news >正文

无涯教程-JavaScript - ISPMT函数

news 2026/2/10 14:03:22

描述

ISPMT函数计算在特定投资期间支付的利息。提供此功能是为了与Lotus 1-2-3兼容。

语法

ISPMT (rate, per, nper, pv)

争论

Argument描述Required/Optional
RateThe interest rate for the investment.Required
PerThe period for which you want to find the interest, and must be between 1 and nper.Required
NperThe total number of payment periods for the investment.Required
Pv

投资的现值。

对于贷款,pv是贷款金额。

Required

Notes

  • 请确保您用于指定费率和nper的单位保持一致

    • 如果您以12％的年利率对四年期贷款进行每月还款,请使用12％/12的利率和4 * 12的nper。

    • 如果您使用同一笔贷款每年还款,则将利率设为12％,将nper设为4。

  • 对于所有参数-

    • 您支付的现金,如存款或其他提款,用负数表示。

    • 您收到的现金,如股息支票和其他存款,用正数表示。

适用性

Excel 2007,Excel 2010,Excel 2013,Excel 2016

Example

ISPMT Function

JavaScript 中的 ISPMT函数 - 无涯教程网无涯教程网提供描述ISPMT函数计算在特定投资期间支付的利息。提供此功能是为了与Lotus 1-2-3兼容。...https://www.learnfk.com/javascript/advanced-excel-financial-ispmt-function.html

相关文章：

无涯教程-JavaScript - ISPMT函数

描述 ISPMT函数计算在特定投资期间支付的利息。提供此功能是为了与Lotus 1-2-3兼容。 语法 ISPMT (rate, per, nper, pv)争论 Argument描述Required/OptionalRateThe interest rate for the investment.RequiredPerThe period for which you want to find the interest, an…...

编程日记 2023/9/11 22:28:53

LeetCode 面试题 03.05. 栈排序

文章目录 一、题目二、C# 题解 一、题目 栈排序。 编写程序，对栈进行排序使最小元素位于栈顶。最多只能使用一个其他的临时栈存放数据，但不得将元素复制到别的数据结构（如数组）中。该栈支持如下操作：push、pop、peek 和…...

编程日记 2023/9/11 22:27:52

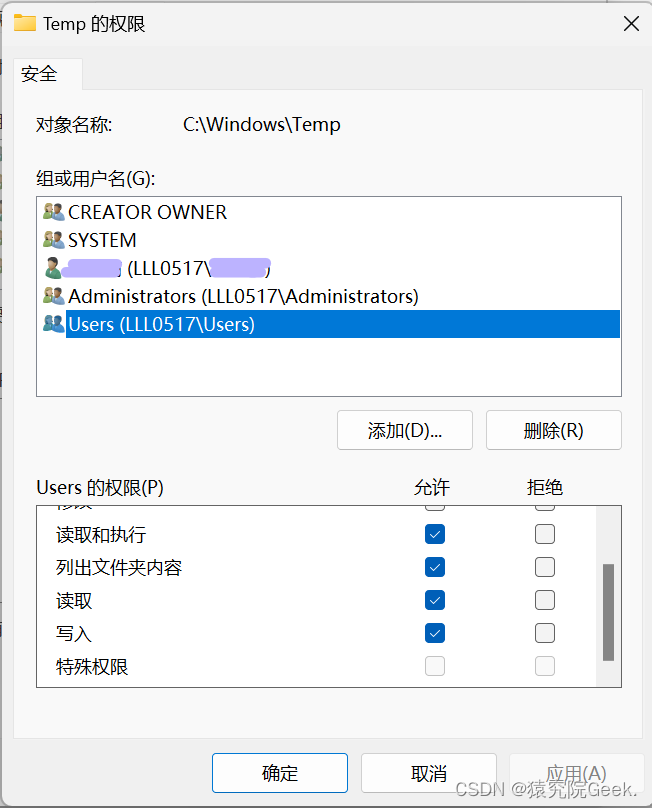
构建微服务项目时启动网关服务失败的解决方案

启动网关服务时报“Unable to create the temporary folder: C:\WINDOWS\TEMP\/nio-file-upload”错误。 代码与之前没有任何变化，但就是启动不了，观察错误意思大概是不能创建临时文件夹：C盘下的WINDOWS下的TEMP目录下的nio-file-upload这个东…...

编程日记 2023/9/11 22:26:50

零基础教程：使用yolov8训练无人机VisDrone数据集

1.准备数据集 1.先给出VisDrone2019数据集的下载地址： 链接：https://pan.baidu.com/s/1e2Q0NgNT-H-Acb2H0Cx8sg 提取码：31dl 2.将数据集VisDrone放在datasets目录下面 2.数据集转换程序 1.在根目录下面新建一个.py文件，取名叫…...

编程日记 2023/9/11 22:25:46

【Mysql专题】使用Mysql做排行榜，线上实例

背景 我们这里有个需求，对存量用户的余额做排行处理，这个实现方式很多，这边介绍的是，通过Mysql直接实现，将排名也直接返回出来。 我知道大家在网上能找到一大把这种实例，我在这里可不是【重复造轮子】。我…...

编程日记 2023/9/11 22:24:46

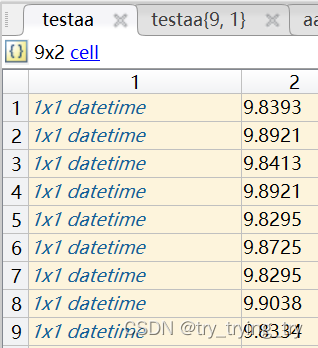
matlab数据处理: cell table array+datetime

原数据文件.csv matlab xlsread(filename{i},B2:T2881) 会同于Excel最多1048576行 舍弃 a{1,i} xlsread(filename{i},‘B2:T2881’);%读取excel文件,选定区域’B2:G2881’ readcell(filename{i},Range,E2:M2881) 会全部读取 优选 对于日期 yyyy-MM-dd HH:mm:ss.000 matlab cel…...

编程日记 2023/9/11 22:23:43

如何应用运营商大数据精准营销？

如何应用运营商大数据精准营销？ 越来越多的企业逐渐觉察到运营商大数据所带来的商业价值，精准营销也被他们用的越来越娴熟。那么，企业的大数据精准营销该如何应用呢？想必是很多资源有限的中小型公司最想了解的。 一 数据驱动运营…...

编程日记 2023/9/11 22:22:40

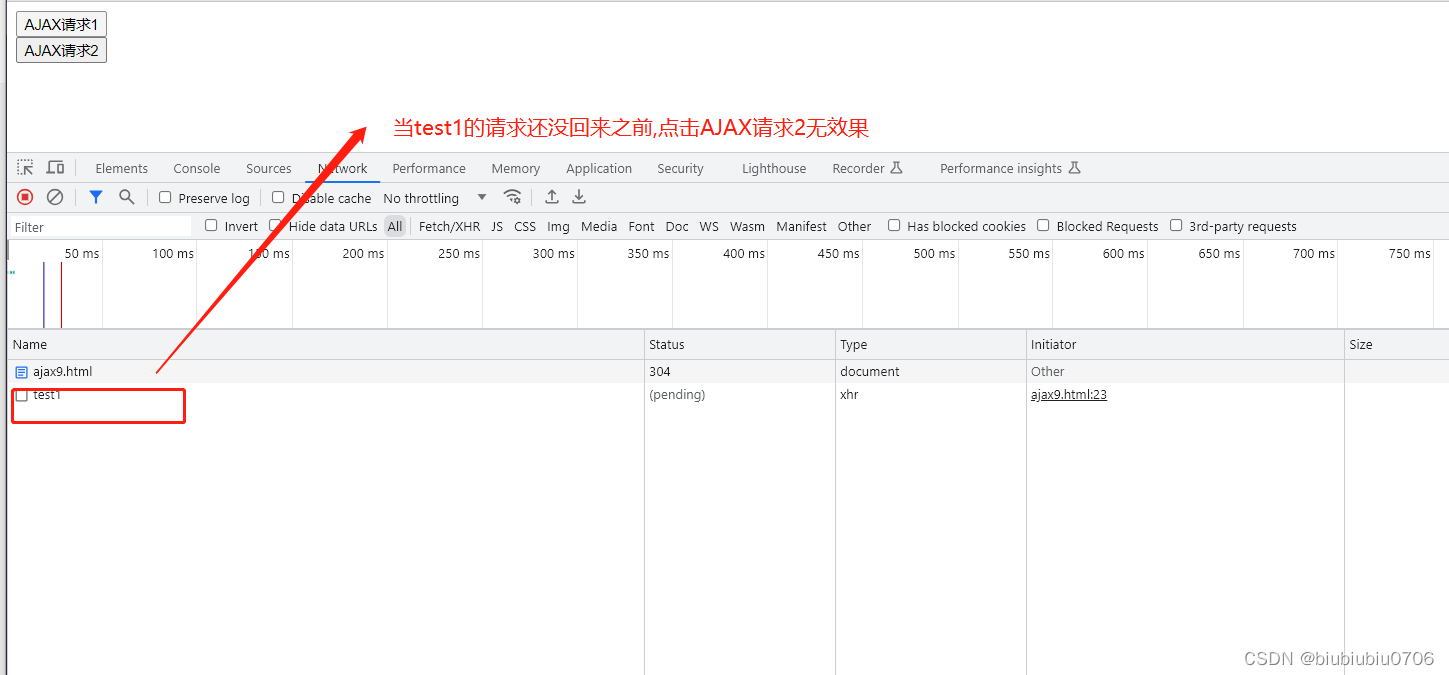
AJAX学习笔记5同步与异步理解

AJAX学习笔记4解决乱码问题_biubiubiu0706的博客-CSDN博客 示例 前端代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>演示AJAX同步和异步</title> </head> <body> <script…...

编程日记 2023/9/11 22:21:18

911面试

WebPack分包 webpack分包 ts泛型 ts泛型 优化if-else和switch 优化if-else 左侧固定&#xff0c;右侧自适应 左侧固定&#xff0c;右侧自适应...

编程日记 2023/9/11 22:20:17

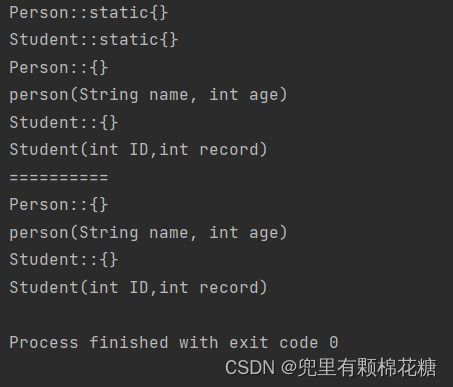
【Java基础篇 | 面向对象】—— 继承

个人主页&#xff1a;兜里有颗棉花糖 欢迎 点赞&#x1f44d; 收藏✨ 留言✉ 加关注&#x1f493;本文由 兜里有颗棉花糖 原创 收录于专栏【JavaSE_primary】 本专栏旨在分享学习JavaSE的一点学习心得&#xff0c;欢迎大家在评论区讨论&#x1f48c; 继承允许一个类继承另一个…...

编程日记 2023/9/11 22:19:15

DELL precision上安装nvidia A4000驱动 cuda cudnn

一、安装驱动 参考这篇文章进行安装Ubuntu安装Nvidia显卡驱动_Kevin__47的博客-CSDN博客 【出现问题】 禁用nouveau后出现黑屏&#xff0c;有几行代码&#xff0c;断线一直在闪 【解决方法】 1、参考这篇文章Ubuntu20.04安装nvidia显卡驱动并解决重启后黑屏问题_ubuntu安装…...

编程日记 2023/9/11 22:18:14

数据结构算法刷题（29）动态规划

思路一&#xff1a;回溯&#xff1a;按照选和不选的判断方式&#xff0c;使用回溯来解决这个问题。 class Solution: def rob(self, nums: List[int]) -> int: n len(nums) #数组的长度 def dfs(i): if i<0: #到达边界条件后 return 0 #返回最大金额是0 res max(dfs(i…...

编程日记 2023/9/11 22:17:12

W11下CMake MinGW配置OpenCV和Qt

&#x1f482; 个人主页:风间琉璃&#x1f91f; 版权: 本文由【风间琉璃】原创、在CSDN首发、需要转载请联系博主&#x1f4ac; 如果文章对你有帮助、欢迎关注、点赞、收藏(一键三连)和订阅专栏哦 前言 前几天将cuda版本的opencv给编译成功了&#xff0c;当时用的VS的MSVC&…...

编程日记 2023/9/11 22:16:10

反转字符串 反转字符串 || 反转字符串 |||

思想总结&#xff1a;首先将字符串转变为字符数组&#xff0c;再进行遍历并反转字符。 1.反转字符串 代码&#xff1a; class Solution {public void reverseString(char[] s) {reverse(s,0,s.length); //左闭右开}public static void reverse(char[] ch,int i,int j) { 翻转函…...

编程日记 2023/9/11 22:15:08

XML解析 不允许有匹配 _[xX][mM][lL]_ 的处理指令目标

以上错误是在解析xml参数时候报出的。 我这里错误的原因在于&#xff0c;<?xml version\"1.0\" encoding\"UTF-8\"?>少了个空格&#xff0c;参考下图&#xff1a; 下面一行才是对的。...

编程日记 2023/9/11 22:14:07

【C++进阶(五)】STL大法--list模拟实现以及list和vector的对比

&#x1f493;博主CSDN主页:杭电码农-NEO&#x1f493;   ⏩专栏分类:C从入门到精通⏪   &#x1f69a;代码仓库:NEO的学习日记&#x1f69a;   &#x1f339;关注我&#x1faf5;带你学习C   &#x1f51d;&#x1f51d; list模拟实现 1. 前言2. list类的大致框架与结构…...

编程日记 2023/9/11 22:13:05

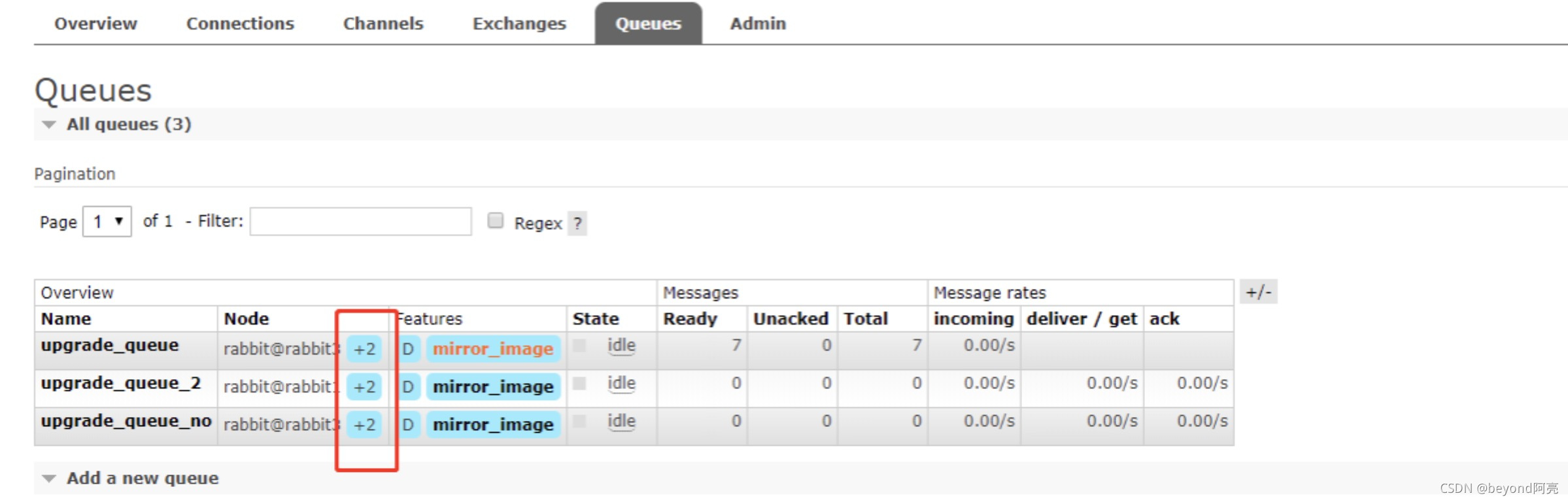
Docker安装RabbitMQ集群_亲测成功

先安装Docker Centos7离线安装Docker 华为云arm架构安装Docker RabbitMQ集群模式介绍 RabbitMQ集群搭建和测试总结_亲测 RabbitMQ 有三种模式&#xff1a;单机模式&#xff0c;普通集群模式&#xff0c;镜像集群模式。单机模式即单独运行一个 rabbitmq 实例&#xff0c;而…...

编程日记 2023/9/11 22:12:04

50道基础数据结构面试题

程序员必备的50道数据结构和算法面试题 在本文中&#xff0c;将分享一些常见的编程面试问题&#xff0c;这些问题来自于不同经验水平的程序员&#xff0c;囊括从刚大学毕业的人到具有一到两年经验的程序员。 编码面试主要包括数据结构和基于算法的问题&#xff0c;以及一些诸…...

编程日记 2023/9/11 22:11:03

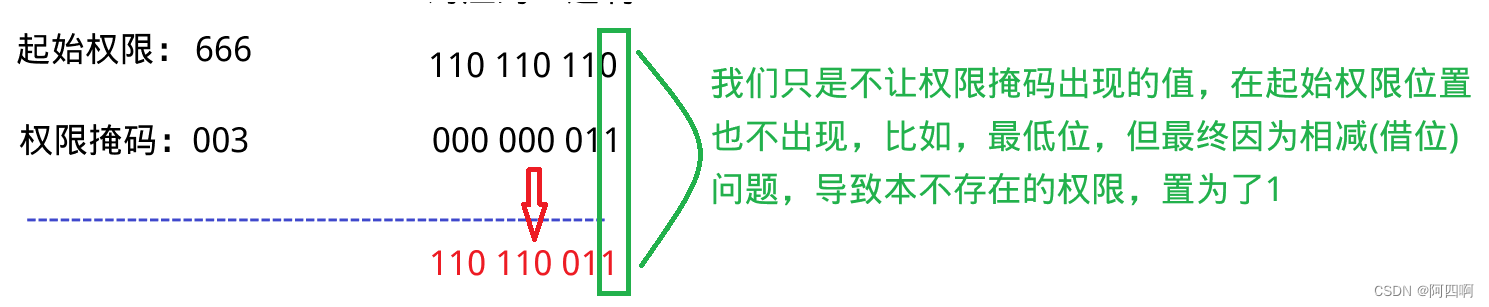
【Linux基础】权限管理

​&#x1f47b;内容专栏&#xff1a; Linux操作系统基础 &#x1f428;本文概括&#xff1a; 用户之间的切换、sudo提权、Linux权限管理、文件访问权限的相关方法、目录权限、粘滞位等 &#x1f43c;本文作者&#xff1a; 阿四啊 &#x1f438;发布时间&#xff1a;2023.9.11 …...

编程日记 2023/9/11 22:10:02

C++初阶--类和对象（中）

目录 类的6个默认成员函数构造函数使用方法 析构函数使用方法 拷贝构造函数使用方法 赋值运算符重载赋值运算符重载 const成员 上篇末尾我们讲到了关于c实现栈相较于c语言在传递参数时的一些优化&#xff0c;但实际上&#xff0c;c在 初始化 清理 赋值 拷贝等方面也做了很大程…...

编程日记 2023/9/11 22:09:00

IDEA运行Tomcat出现乱码问题解决汇总

最近正值期末周&#xff0c;有很多同学在写期末Java web作业时&#xff0c;运行tomcat出现乱码问题&#xff0c;经过多次解决与研究&#xff0c;我做了如下整理&#xff1a; 原因&#xff1a; IDEA本身编码与tomcat的编码与Windows编码不同导致&#xff0c;Windows 系统控制台…...

编程新知 2026/2/10 11:13:58

HTML 语义化

目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案&#xff1a; 语义化标签&#xff1a; <header>&#xff1a;页头<nav>&#xff1a;导航<main>&#xff1a;主要内容<article>&#x…...

编程新知 2026/1/15 21:24:41

设计模式和设计原则回顾

设计模式和设计原则回顾 23种设计模式是设计原则的完美体现，设计原则设计原则是设计模式的理论基石， 设计模式 在经典的设计模式分类中（如《设计模式：可复用面向对象软件的基础》一书中），总共有23种设计模式，分为三大类： 一、创建型模式（5种） 1. 单例模式（Sing…...

编程新知 2025/12/14 20:57:41

2025 后端自学UNIAPP【项目实战：旅游项目】6、我的收藏页面

代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口&#xff08;适配服务端返回 Token&#xff09; export const login async (code, avatar) > {const res await http…...

编程新知 2026/1/29 11:40:13

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码： prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

编程新知 2025/7/4 0:50:01

云原生玩法三问：构建自定义开发环境

云原生玩法三问&#xff1a;构建自定义开发环境 引言 临时运维一个古董项目&#xff0c;无文档&#xff0c;无环境&#xff0c;无交接人&#xff0c;俗称三无。 运行设备的环境老&#xff0c;本地环境版本高&#xff0c;ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

编程新知 2026/2/2 9:25:26

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

Spring Security 认证流程——补充

一、认证流程概述 Spring Security 的认证流程基于 过滤器链&#xff08;Filter Chain&#xff09;&#xff0c;核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤&#xff1a; 用户提交登录请求拦…...

编程新知 2026/2/4 17:50:55

链式法则中 复合函数的推导路径 多变量“信息传递路径”

非常好&#xff0c;我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题&#xff0c;统一使用 二重复合函数&#xff1a; z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y))​ 来全面说明。我们会展示其全微分形式&#xff08;偏导…...

编程新知 2026/2/8 12:07:50

MySQL体系架构解析（三）：MySQL目录与启动配置全解析

MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录&#xff0c;这个目录下存放着许多可执行文件。与其他系统的可执行文件类似&#xff0c;这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中&#xff0c;用…...

编程新知 2026/1/23 12:07:06