电池的健康状态 SOH 估计
电池的健康状态 SOH 估计
SOH(State of Health)估计通常用于描述电池的健康状态,即电池当前容量与初始容量的比值。
一种常见的SOH估计方法是基于经验的电池寿命预测方法,包括循环周期数法、安时法与加权安时法、面向事件的老化累积方法。这些方法都是利用电池使用过程中的一些经验知识,依据某些统计学规律给出电池寿命的一个粗略估计,只适用于电池使用的经验知识比较充分的情况下,用于特定场合的寿命预测。
另一种SOH估计方法是基于耐久性模型的开环方法,这种方法描述了固体电解质膜电阻和电池端子电压的增加,对电池内部的物理化学反应的特性进行分析,了解电化学反应特性和电池容量衰退的本质,从而直接预测容量衰减和内阻的变化。
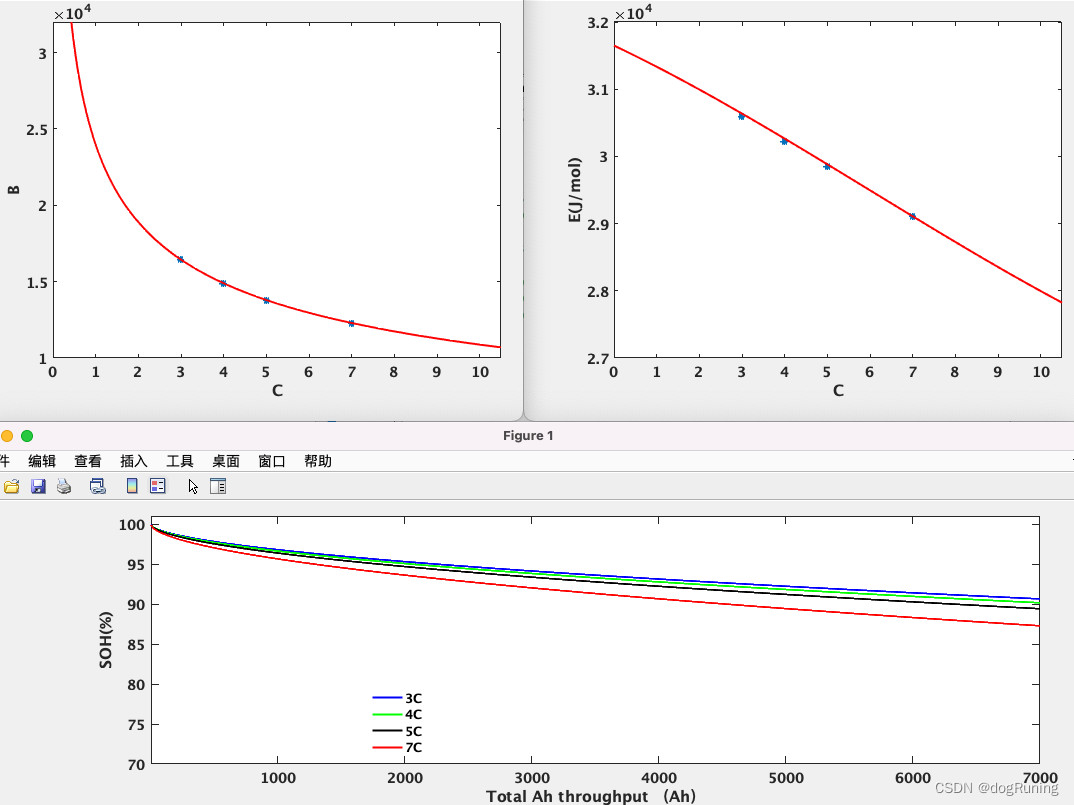
T=298.15%25度的绝对温度 for i=1:9000% Q(i)=30330*exp(-31500/(8.314*T))*i.^0.552;
Q1(i)=16437*exp((-31700+370.3*3)/(8.314*T))*i.^0.55; %0.5C
Q2(i)=14892*exp((-31700+370.3*4)/(8.314*T))*i.^0.55; %2C
Q3(i)=13795*exp((-31700+370.3*5)/(8.314*T))*i.^0.55; %6C
Q4(i)=12291*exp((-31700+370.3*7)/(8.314*T))*i.^0.55; %10Cend
figure
plot(100-Q1,'-b','linewidth',2')
hold onplot(100-Q2,'-G','linewidth',2)
hold on
plot(100-Q3,'-K','linewidth',2)
hold on
plot(100-Q4,'-r','linewidth',2)
legend('3C','4C','5C','7C','Location','best');
legend('boxoff')set(gca,'xtick',[0:1000:10000]);
set(gca,'ytick',[0:5:110]);
axis([1 7000 70 101]);set (gca,'position',[0.16,0.15,0.8,0.8] );
set(gca,'Fontsize',14);xlabel('Total Ah throughput (Ah)','FontName','Microsoft YaHei','FontWeight','Bold','FontSize',15)ylabel('SOH(%)','FontName','Times New Roman','FontWeight','Bold','FontSize',15)
set(gca,'FontName','Microsoft YaHei','FontWeight','Bold','FontSize',14)
B与倍率的关系
C=[3 4 5 7];%倍率B=[16437 14892 13795 12291];B1=@(i)2.396e+04*abs(i).^(-0.343);figureplot(C,B,'*','linewidth',2)hold onfplot(@(x)B1(x),[0 11],'r','linewidth',2)set(gca,'xtick',[0:1:11]);set(gca,'ytick',[0:5000:40000]);axis([0 10.5 10000 32001]);set (gca,'position',[0.16,0.15,0.8,0.8] );set(gca,'Fontsize',14);xlabel('C','FontName','Microsoft YaHei','FontWeight','Bold','FontSize',15)ylabel('B','FontName','Times New Roman','FontWeight','Bold','FontSize',15)set(gca,'FontName','Microsoft YaHei','FontWeight','Bold','FontSize',14)单纯倍率的模型参数
C=[3 4 5 7 ];
E=[30589 30218 29848 29107 ];p1 = 0.7974p2 = -14.35p3 = -301.6p4 = 3.165e+04 E1=@(x)p1*x^3+p2*x^2+p3*x+p4figure
plot(C,E,'*','linewidth',2)
hold on
fplot(@(x)E1(x),[0 11],'r','linewidth',2)
set(gca,'xtick',[0:1:11]);
set(gca,'ytick',[0:1000:50000]);
axis([0 10.5 27000 32001]);set (gca,'position',[0.16,0.15,0.8,0.8] );
set(gca,'Fontsize',14);xlabel('C','FontName','Microsoft YaHei','FontWeight','Bold','FontSize',15)ylabel('E(J/mol)','FontName','Times New Roman','FontWeight','Bold','FontSize',15)
set(gca,'FontName','Microsoft YaHei','FontWeight','Bold','FontSize',14)
相关文章:

电池的健康状态 SOH 估计
电池的健康状态 SOH 估计 SOH(State of Health)估计通常用于描述电池的健康状态,即电池当前容量与初始容量的比值。 一种常见的SOH估计方法是基于经验的电池寿命预测方法,包括循环周期数法、安时法与加权安时法、面向事件的老化…...
详解)
Web 安全之 Permissions Policy(权限策略)详解
什么是 Permissions Policy(权限策略)? Permissions Policy 为 web 开发人员提供了明确声明哪些功能可以在网站上使用,哪些功能不能在网站上使用的机制。可以设置一组策略,用于限制站点代码可以访问的 API 或者修改浏…...

【黄啊码】nginx如何设置php运行的
禁止访问 PHP 脚本可以通过 Nginx 服务器配置中的多种方式来实现。以下是其中的一些常见方法,您可以根据实际需求选择合适的方式: 1 禁用 PHP 解析: 在 Nginx 配置中,确保 PHP 脚本无法被解析,从而禁止 PHP 执行。 lo…...

无涯教程-JavaScript - ISPMT函数
描述 ISPMT函数计算在特定投资期间支付的利息。提供此功能是为了与Lotus 1-2-3兼容。 语法 ISPMT (rate, per, nper, pv)争论 Argument描述Required/OptionalRateThe interest rate for the investment.RequiredPerThe period for which you want to find the interest, an…...

LeetCode 面试题 03.05. 栈排序
文章目录 一、题目二、C# 题解 一、题目 栈排序。 编写程序,对栈进行排序使最小元素位于栈顶。最多只能使用一个其他的临时栈存放数据,但不得将元素复制到别的数据结构(如数组)中。该栈支持如下操作:push、pop、peek 和…...
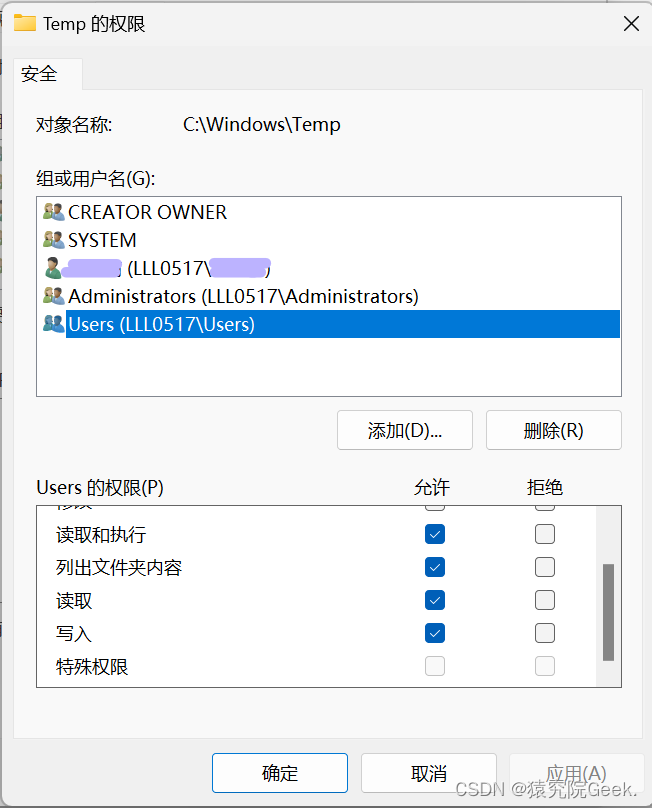
构建微服务项目时启动网关服务失败的解决方案
启动网关服务时报“Unable to create the temporary folder: C:\WINDOWS\TEMP\/nio-file-upload”错误。 代码与之前没有任何变化,但就是启动不了,观察错误意思大概是不能创建临时文件夹:C盘下的WINDOWS下的TEMP目录下的nio-file-upload这个东…...
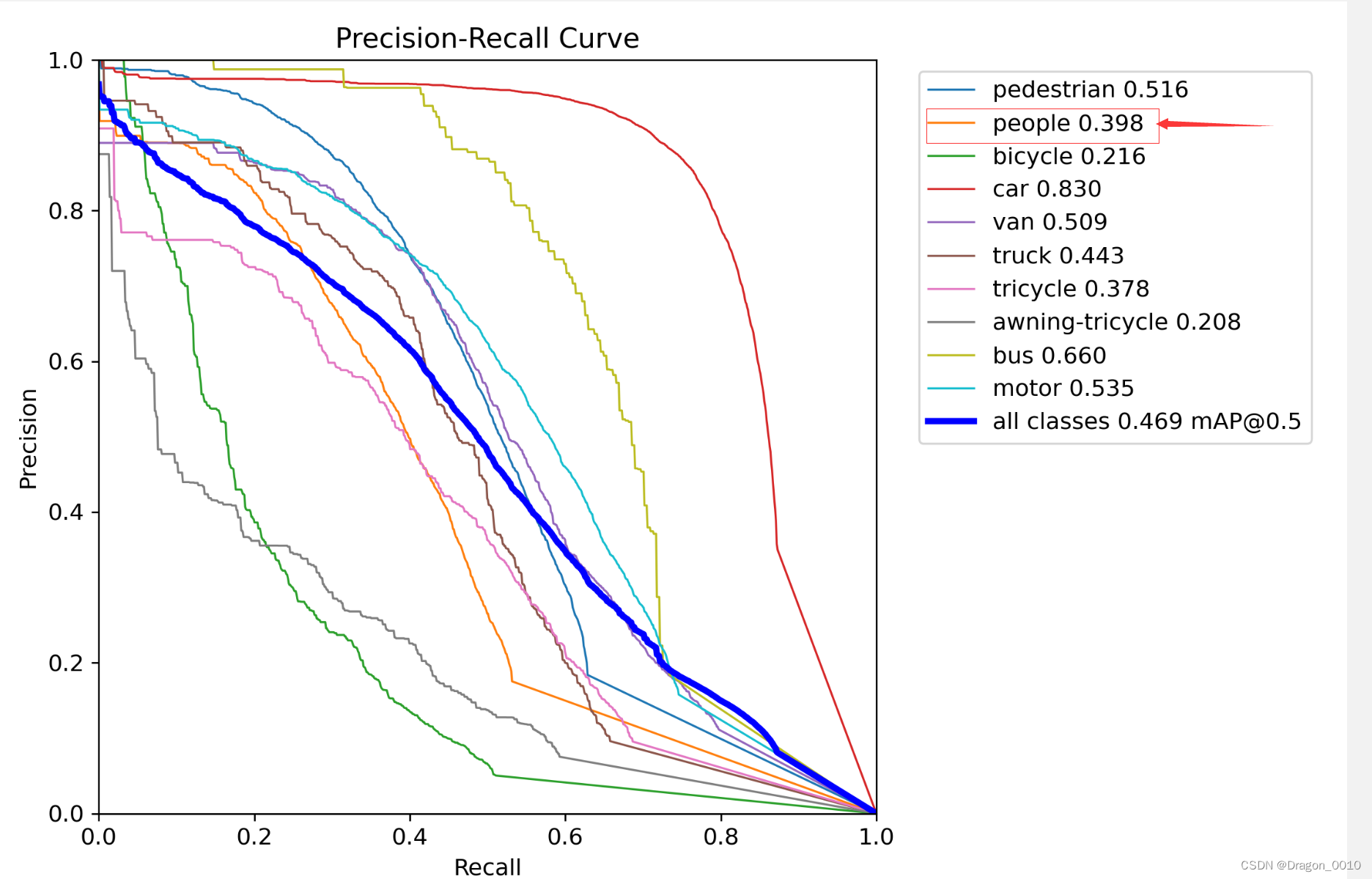
零基础教程:使用yolov8训练无人机VisDrone数据集
1.准备数据集 1.先给出VisDrone2019数据集的下载地址: 链接:https://pan.baidu.com/s/1e2Q0NgNT-H-Acb2H0Cx8sg 提取码:31dl 2.将数据集VisDrone放在datasets目录下面 2.数据集转换程序 1.在根目录下面新建一个.py文件,取名叫…...

【Mysql专题】使用Mysql做排行榜,线上实例
背景 我们这里有个需求,对存量用户的余额做排行处理,这个实现方式很多,这边介绍的是,通过Mysql直接实现,将排名也直接返回出来。 我知道大家在网上能找到一大把这种实例,我在这里可不是【重复造轮子】。我…...
matlab数据处理: cell table array+datetime
原数据文件.csv matlab xlsread(filename{i},B2:T2881) 会同于Excel最多1048576行 舍弃 a{1,i} xlsread(filename{i},‘B2:T2881’);%读取excel文件,选定区域’B2:G2881’ readcell(filename{i},Range,E2:M2881) 会全部读取 优选 对于日期 yyyy-MM-dd HH:mm:ss.000 matlab cel…...
如何应用运营商大数据精准营销?
如何应用运营商大数据精准营销? 越来越多的企业逐渐觉察到运营商大数据所带来的商业价值,精准营销也被他们用的越来越娴熟。那么,企业的大数据精准营销该如何应用呢?想必是很多资源有限的中小型公司最想了解的。 一 数据驱动运营…...
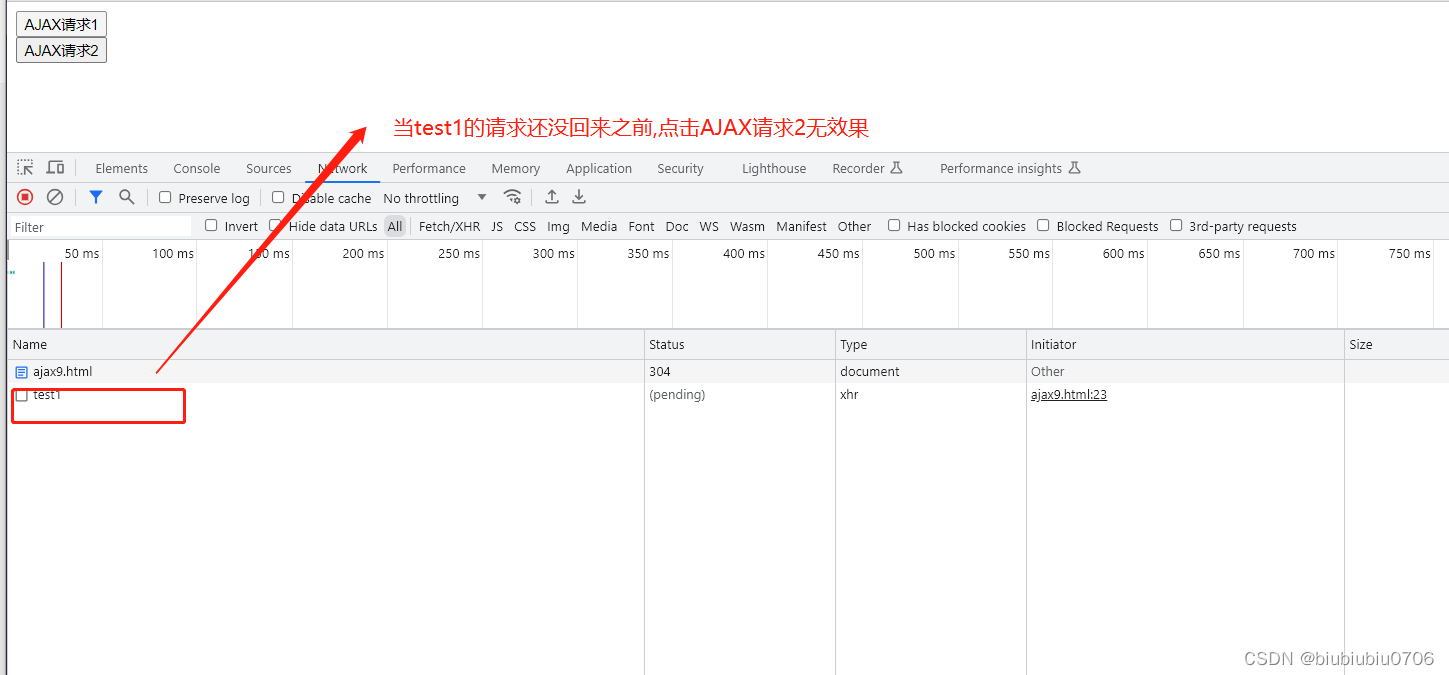
AJAX学习笔记5同步与异步理解
AJAX学习笔记4解决乱码问题_biubiubiu0706的博客-CSDN博客 示例 前端代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>演示AJAX同步和异步</title> </head> <body> <script…...

911面试
WebPack分包 webpack分包 ts泛型 ts泛型 优化if-else和switch 优化if-else 左侧固定,右侧自适应 左侧固定,右侧自适应...
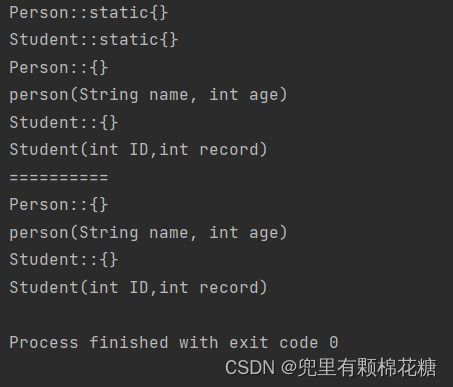
【Java基础篇 | 面向对象】—— 继承
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【JavaSE_primary】 本专栏旨在分享学习JavaSE的一点学习心得,欢迎大家在评论区讨论💌 继承允许一个类继承另一个…...

DELL precision上安装nvidia A4000驱动 cuda cudnn
一、安装驱动 参考这篇文章进行安装Ubuntu安装Nvidia显卡驱动_Kevin__47的博客-CSDN博客 【出现问题】 禁用nouveau后出现黑屏,有几行代码,断线一直在闪 【解决方法】 1、参考这篇文章Ubuntu20.04安装nvidia显卡驱动并解决重启后黑屏问题_ubuntu安装…...

数据结构算法刷题(29)动态规划
思路一:回溯:按照选和不选的判断方式,使用回溯来解决这个问题。 class Solution: def rob(self, nums: List[int]) -> int: n len(nums) #数组的长度 def dfs(i): if i<0: #到达边界条件后 return 0 #返回最大金额是0 res max(dfs(i…...

W11下CMake MinGW配置OpenCV和Qt
💂 个人主页:风间琉璃🤟 版权: 本文由【风间琉璃】原创、在CSDN首发、需要转载请联系博主💬 如果文章对你有帮助、欢迎关注、点赞、收藏(一键三连)和订阅专栏哦 前言 前几天将cuda版本的opencv给编译成功了,当时用的VS的MSVC&…...

反转字符串 反转字符串 || 反转字符串 |||
思想总结:首先将字符串转变为字符数组,再进行遍历并反转字符。 1.反转字符串 代码: class Solution {public void reverseString(char[] s) {reverse(s,0,s.length); //左闭右开}public static void reverse(char[] ch,int i,int j) { 翻转函…...

XML解析 不允许有匹配 _[xX][mM][lL]_ 的处理指令目标
以上错误是在解析xml参数时候报出的。 我这里错误的原因在于,<?xml version\"1.0\" encoding\"UTF-8\"?>少了个空格,参考下图: 下面一行才是对的。...

【C++进阶(五)】STL大法--list模拟实现以及list和vector的对比
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 list模拟实现 1. 前言2. list类的大致框架与结构…...
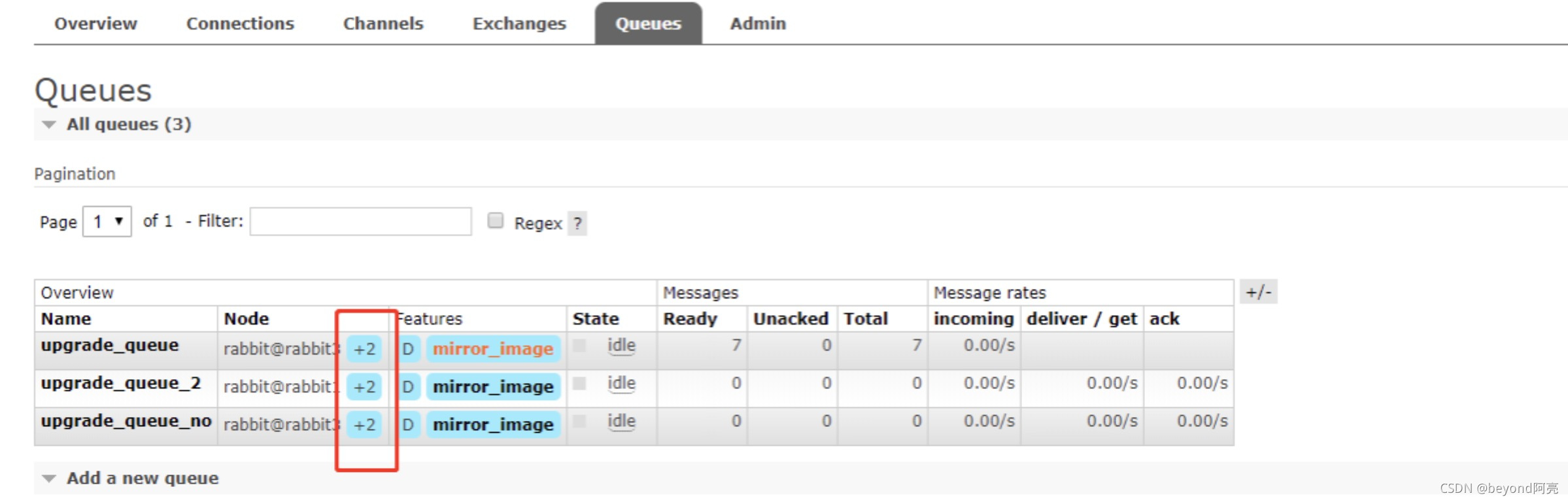
Docker安装RabbitMQ集群_亲测成功
先安装Docker Centos7离线安装Docker 华为云arm架构安装Docker RabbitMQ集群模式介绍 RabbitMQ集群搭建和测试总结_亲测 RabbitMQ 有三种模式:单机模式,普通集群模式,镜像集群模式。单机模式即单独运行一个 rabbitmq 实例,而…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
