2024届校招-Java开发笔试题-S4卷
有三种题型:单项选择题(10道)、不定项选择题(10道)、编程题(3道)
下面是一些回忆的题目:
1.哪种设计模式将对象的创建与使用分离,通过工厂类创建对象
答:工厂模式
工厂模式是一种创建型设计模式,它旨在将对象的创建与使用分离。通过引入一个工厂类,客户端代码可以委托工厂类来创建所需的对象,而不必直接实例化对象。这有助于降低耦合度并提高代码的可维护性。
2.运行中的线程,执行Thread.sleep(5000)方法后,,当时间过去5s后,线程状态为
答:可运行(Runnable)状态,等待系统调度来继续执行。
3.new java.math.Big Decimal(0.1)是否会丢失精度
答:不会,BigDecimal类是用来表示精确的任意精度的十进制数,不会引发浮点数的精度问题。然而,如果使用浮点数字面值(例如0.1)来初始化BigDecimal,那么在转换过程可能会引发精度问题,应使用字符串初始化BigDecimal,直接将字符串文本转换为BigDecimal。
4.关于@Import注解的选择题
答:@Import注解是Java Spring 框架中的一个注解,用于在配置类中引入其他配置类,从而将它们的配置合并到当前配置中。它允许开发者在一个配置类中引入其他配置,以便组织和管理Spring应用程序的配置。
@Import注解动态注入方式可通过使用ImportSelector接口的类来实现。但并不是唯一的方式,还可以通过条件化的@Import注解、编程方式的条件化注入、条件化的BeanDefinition注册。
5.创建型设计模式有哪些?
答:创建型设计模式是一种软件设计模式,它们关注如何创建对象,以便在应用程序中更灵活、更高效地管理对象的创建和初始化。以下是一些常见的创建型设计模式:单例模式(Singleton Pattern)、工厂模式(Factory Pattern)、抽象工厂模式(Abstract Factory Pattern)、建造者模式(Builder Pattern)、原型模式(Prototype Pattern)
6.快速排序最坏时间复杂度?
O(n^2),平均时间复杂度为O(n*log(n))
7.匹配“一”“二”“三”……“十”的中文正则表达式是
[一二三四五六七八九十]
8.哪些场景适合使用NIO模型?
Java NIO(New I/O)模型适合处理需要高并发、高吞吐量和低延迟的网络通信和文件I/O场景。以下是一些适合使用NIO模型的常见场景:网络编程、文件I/O、多路复用、实时数据处理、高性能代理和网关
9.哪些集合类是线程安全的?
答:集合类的线程安全意味着多个线程可以同时访问和修改这些集合而不会导致数据不一致或抛出并发异常。以下是一些线程安全的集合类:Vector、HashTable、ConcurrentHashMap、CopyOnWriteArrayList、CopyOnWriteArraySet、ConcurrentLinkedQueue、BlockingQueue。
10.哪些属于进程同步机制?
答:线程同步机制是用于协调和管理多个进程之间的执行顺序以及访问共享资源的一组技术。以下是一些常见的进程同步机制:互斥锁(Mutex)、信号量(Semaphore)、条件变量(Condition Variable)、屏障(Barrier)、读写锁(Read-Write Lock)、管程(Monitor)、自旋锁(Spin Lock)、消息传递
-
当浏览器缓存中有缓存版本时,哪个HTTP响应头字段可以用于验证缓存是否仍然有效
答:ETag(实体标签)、Last-Modified(最后修改时间) -
哪些可以增强Cookie的安全性
答:使用HTTPOnly标志;使用Secure标志、设置Cookie的SameSite属性;限制Cookie的有效期;对Cookie的内容进行加密;在服务器端验证Cookie;实施双重身份验证(2FA);定期更改Cookie值;监控和审计;
编程题:
- 有n个城市通过m个航班连接。每个航班都从城市u开始,以价格w抵达v。现在给定所有的城市和航班,以及出发城市src,你的任务是找到从src城市出发到其他所有城市最便宜的机票价格列表。
如果无法从src到达某个城市,则他们的价格-1表示。
输入n=3,edges=[[0,1,100],[1,2,100],[0,2,500],src=0
输出:[0,100,200]
/*** 有n个城市通过m个航班连接。每个航班都从城市u开始,以价格w抵达v。现在给定所有的城市和航班,以及出发城市src,* 你的任务是找到从src城市出发到其他所有城市最便宜的机票价格列表。* 如果无法从src到达某个城市,则他们的价格-1表示。** 输入n=3,edges=[[0,1,100],[1,2,100],[0,2,500],src=0* 输出:[0,100,200]***/import java.util.*;
public class CheapestPrices {public int[] findCheapestPrice(int n, int[][] flights, int src) {//n代表城市个数//flights 是一个包含多个一维数组的二维数组。每个一维数组都表示一条航班的信息,//flights[i][0] 是起始城市的编号,flights[i][1] 是目标城市的编号,flights[i][2] 是航班的价格。//src 代表出发城市,题目的意思就是要找出从src出发到其他所有城市出发最便宜的价格。// 创建一个邻接表来表示城市之间的航班价格List<int[]>[] graph = new List[n];//graph[i] 存储与城市 i 相关的航班信息。for (int i = 0; i < n; i++) {graph[i] = new ArrayList<>();//表示每个索引 i 处的元素都是一个空的整数数组列表。}for (int[] flight : flights) { //这段循环用于将航班信息从二维数组 flights 添加到图数据结构 graph 中int u = flight[0];int v = flight[1];int w = flight[2];graph[u].add(new int[]{v, w});//将一个新的整数数组 {v, w} 添加到列表中}// 初始化距离数组,初始距离为无穷大int[] distances = new int[n];//该数组用来存储从出发城市 src 到其他城市的距离信息Arrays.fill(distances, Integer.MAX_VALUE);distances[src] = 0;//将出发城市 src 到自身的距离设置为0// 使用最小堆来进行Dijkstra算法PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b) -> a[1] - b[1]);//minHeap用于存储待处理的节点minHeap.offer(new int[]{src, 0});//将出发城市 src 到自身的距离为0的节点添加到优先队列while (!minHeap.isEmpty()) {int[] current = minHeap.poll();//从优先队列 minHeap 中取出队首元素,即距离最短的节点int currentCity = current[0];//current[0] 表示当前节点的城市编号int currentCost = current[1];//current[1] 表示从起始城市到当前城市的距离。//用于检查当前节点的距离是否已经被更新过//如果 currentCost 大于 distances[currentCity],//则表示已经有更短的路径到达当前城市,因此可以忽略当前节点,继续处理下一个节点if (currentCost > distances[currentCity]) {continue;}for (int[] neighbor : graph[currentCity]) {int neighborCity = neighbor[0];//neighbor[0] 表示邻居城市的编号int neighborCost = neighbor[1];//neighbor[1] 表示从当前城市到邻居城市的距离(权重)。int newCost = currentCost + neighborCost;if (newCost < distances[neighborCity]) {distances[neighborCity] = newCost;minHeap.offer(new int[]{neighborCity, newCost});//将该数组添加到优先队列 minHeap 中,以便稍后继续处理该邻居节点。// 这确保了算法在接下来的迭代中考虑到了邻居节点。}}//通过这段循环,算法不断地探索从当前节点到其邻居节点的可能路径,并更新到达邻居节点的最短距离。// 如果找到更短的路径,就会将邻居节点添加到优先队列中,以便后续继续处理。这是Dijkstra算法的关键步骤,// 确保找到从出发城市到其他城市的最短路径。}// 将无法到达的城市的距离设为-1for (int i = 0; i < n; i++) {if (distances[i] == Integer.MAX_VALUE) {distances[i] = -1;}}return distances;}public static void main(String[] args) {CheapestPrices solution = new CheapestPrices();int n = 3;int[][] edges = {{0, 1, 100}, {1, 2, 100}, {0, 2, 500}};int src = 0;int[] output = solution.findCheapestPrice(n, edges, src);// 输出最便宜的机票价格列表for (int price : output) {System.out.print(price + " ");}// 输出: 0 100 200}
}2.给定一个任意矩阵(用二维数组表示),要求从左上角移动至右下角,每次只能向下或向右移动一格,矩阵中的数字为本次移动的收益,请算出移动值右下角时,所经过路径和的最大收益。
import java.util.*;public class maxPathSum {public static int maxPathSum(int[][] matrix){if(matrix==null||matrix.length==0||matrix[0].length == 0){return 0;}int m = matrix.length;int n = matrix[0].length;int dp[][] = new int[m][n];dp[0][0] = matrix[0][0];for(int j=1;j<n;j++){dp[0][j] = dp[0][j-1]+matrix[0][j];}for(int i=1;i<n;i++){dp[i][0] = dp[i-1][0] + matrix[i][0];}for(int i=1;i<m;i++){for(int j=1;j<n;j++){dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1])+matrix[i][j];}}return dp[m-1][n-1];}public static void main(String[] args) {int [][] matrix={{1,2,3},{4,7,6},{5,8,9},};int maxSum = maxPathSum(matrix);System.out.println("最大路径和为:"+maxSum);}
}3.在一个遥远的银河中,有N个星球(编号从1到N),这些星球之间通过星际门进行连接。每个星际门都连接两个星球,并旦可以双向通行。
每个星际门的开启需要消耗一定的能量,这个能量由星际门上的数字表示。每个星际门上的数字都是唯一的。
现在,由于某种原因,所有的星际门都处于 关闭状态。作为一个探索者,你的任务是找出一种方式,开启最少的星际门,使得所有的星球都至少通过一个开启的星际门与其他星球连接。
给你一些可连接的选项 connections,其中connections[i] = [Xi, Yi, Mi] 表示星球 Xi和星球Yi之间可以开启一个星际门工并消耗 Mi 能量。
计算联通所有星球所需的最小能量消耗。如果无法联通所有星球,则输出-1。
import java.util.*;
import java.util.Arrays;
public class Solution1 {public static int minimumEnergyRequired(int N,int[][] connections){Arrays.sort(connections,(a,b)->a[2]-b[2]);int[] parent = new int[N+1];//parent[i] 存储了元素i的父节点的编号,// 如果 parent[i] 的值为-1,表示元素i是自身所在集合的根节点。Arrays.fill(parent,-1);int minEnergy = 0;int numEdges = 0;for(int[] connection:connections){int front = connection[0];int to = connection[1];int energy = connection[2];int rootFrom = findRoot(parent,front);int rootTo = findRoot(parent, to);if(rootFrom!=rootTo){parent[rootFrom] = rootTo;minEnergy += energy;numEdges++;//已经合并的星际门数量if(numEdges==N-1){return minEnergy;}}}return -1;}//它的作用是查找某个节点在并查集中所属的集合的根节点,并在查找过程中进行路径压缩,private static int findRoot(int[] parent,int node){if(parent[node] == -1){return node;}parent[node] = findRoot(parent,parent[node]);//这一步是路径压缩的关键,它将节点 node 的父节点直接设置为根节点,// 从而优化后续的查找操作。return parent[node];}public static void main(String[] args) {int N=4;int[][] connections = {{1,2,5},{1,3,6},{2,3,1},{3,4,2},{2,4,3},};int result = minimumEnergyRequired(N,connections);System.out.println("最小能量消耗为:"+result);}
}相关文章:

2024届校招-Java开发笔试题-S4卷
有三种题型:单项选择题(10道)、不定项选择题(10道)、编程题(3道) 下面是一些回忆的题目: 1.哪种设计模式将对象的创建与使用分离,通过工厂类创建对象 答:工…...
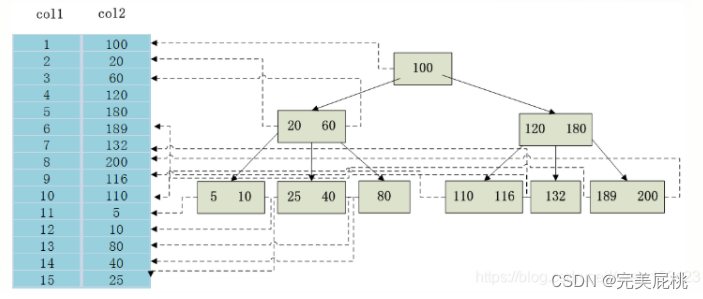
数据分析面试题(2023.09.08)
数据分析流程 总体分为四层:需求层、数据层、分析层和结论层 一、统计学问题 1、贝叶斯公式复述并解释应用场景 公式:P(A|B) P(B|A)*P(A) / P(B)应用场景:如搜索query纠错,设A为正确的词,B为输入的词,那…...

jenkins 报错fatal:could not read Username for ‘XXX‘:No such device or address
#原因:机器做迁移,或者断电,遇到突发情况 #解决: 一.排查HOME和USER环境变量 可以在项目执行shell脚本的时候echo $HOME和USER 也可以在构建记录位置点击compare environment 对比两次构建的环境变量 二.查看指定节点的git凭证 查…...
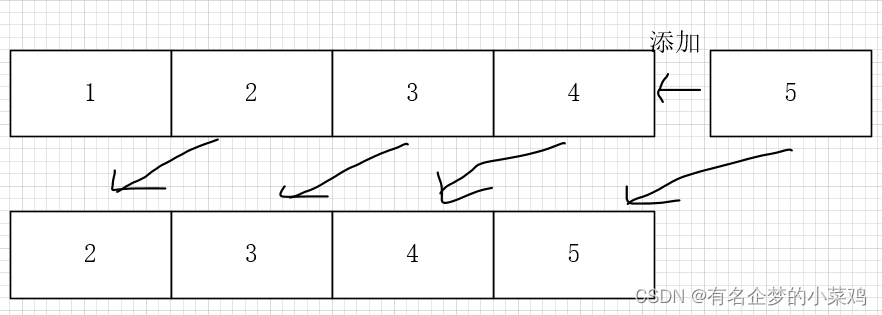
LRU算法之我见
文章目录 一、LRU算法是什么?二、使用原理三、代码实现总结 一、LRU算法是什么? LRU算法又称最近最少使用算法,它是是大部分操作系统为最大化页面命中率而广泛采用的一种页面置换算法。是一种缓存淘汰策略,根据使用频率来淘汰无用…...
)
【第20例】华为 IPD 体系 | IPD 的底层思考逻辑(限制版)
目录 简介 更新情况 IPD体系 CSDN学院 专栏目录 作者简介 简介 最近随着华为 Mate 60 系列的爆火发布。 这家差不多沉寂了 4 年的企业再次映入大众的眼帘。 其实,华为手机业务发展的元年最早可以追溯...
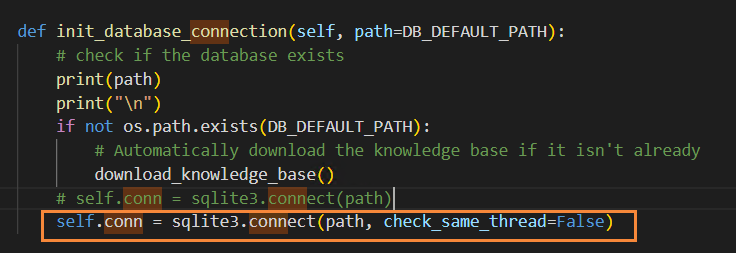
spaCy库的实体链接踩坑,以及spaCy-entity-linker的knowledge_base下载问题
问题1. spacy Can’t find factory for ‘entityLinker’ 1)问题 写了一个实体链接类,代码如下: nlp spacy.load("en_core_web_md")class entieyLink:def __init__(self, doc, nlp):self.nlp nlpself.doc self.nlp(doc)# Che…...
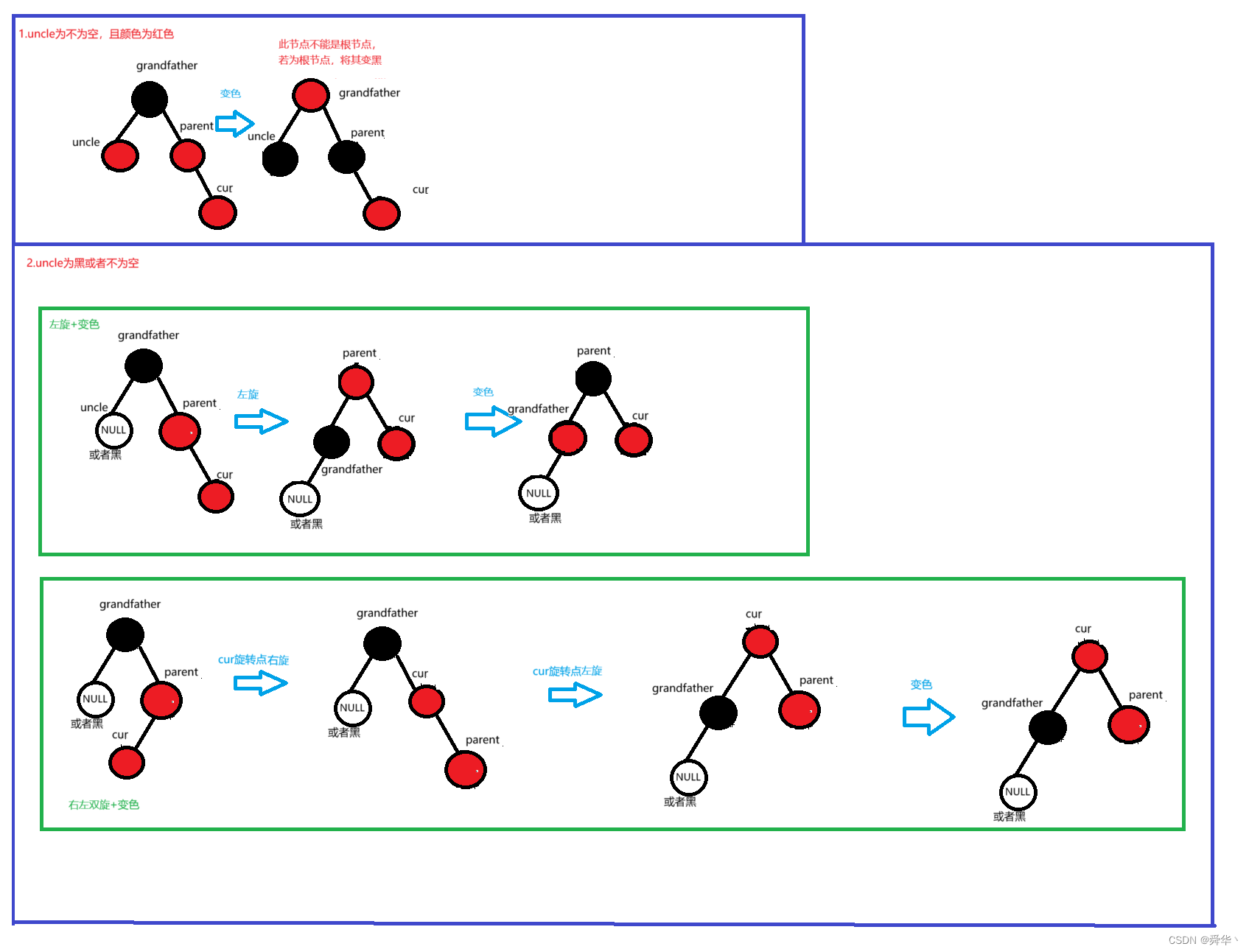
【数据结构】红黑树的插入与验证
文章目录 一、基本概念1.时代背景2. 基本概念3.基本性质 二、实现原理1. 插入1.1变色1.2旋转变色①左旋②右旋③右左双旋④左右双旋 2.验证 源码总结 一、基本概念 1.时代背景 1972年鲁道夫拜尔(Rudolf Bayer)发明了一种数据结构,这是一种特殊的B树4阶情况。这些树…...
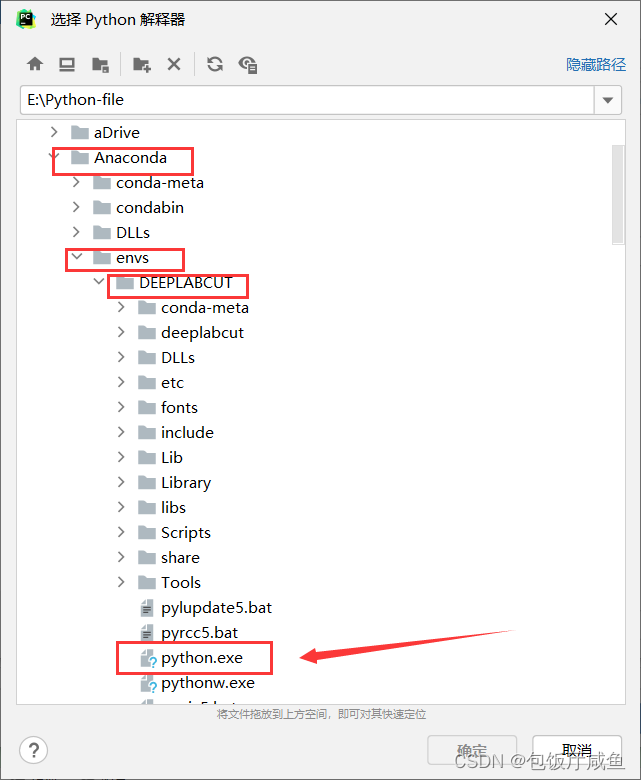
Pycharm----将Anaconda建立的环境导入
首先打开项目设置,点击添加 随后点击现有环境,点击三个。。。号进行添加 最后找到你Anaconda安装文件夹,envs找到你建立的环境名称,找到python.exe将它导入即可让现在的python环境为你建立的环境,同时还需要更改终端方…...

数字花园的指南针:微信小程序排名的提升之道
微信小程序,是一片数字花园,其中各种各样的小程序竞相绽放,散发出各自独特的芬芳。在这个花园中,排名优化就像是精心照料花朵的园丁,让我们一同走进这个数字花园,探寻如何提升微信小程序的排名优化…...

LRU与LFU的c++实现
LRU 是时间维度上最少使用 维持一个链表,最近使用的放在表头 淘汰表尾 LFU 是实际使用频率的最少使用 每一个对应的频率维持一个链表, 淘汰最低频率的最后一个 1. LRU LRU(Least Recently Used,最近最少使用)是一种常…...

什么是Docker和Docker-Compose?
Docker的构成 Docker仓库:https://hub.docker.com Docker自身组件 Docker Client:Docker的客户端 Docker Server:Docker daemon的主要组成部分,接受用户通过Docker Client发出的请求,并按照相应的路由规则实现路由分发…...
三.listview或tableviw显示
一.使用qt creator 转变类型 变形为listview或tableviw 二.导出ui文件为py文件 # from123.py 为导出 py文件 form.ui 为 qt creator创造的 ui 文件 pyuic5 -o x:\xxx\from123.py form.uifrom123.py listview # -*- coding: utf-8 -*-# Form implementation generated fro…...
【算法】一文带你从浅至深入门dp动态规划
文章目录 一、前言二、动态规划理论基础1、基本概念2、动态规划五部曲【✔】3、出错了如何排查? 三、实战演练🗡0x00 斐波那契数0x01 第N个泰波那契数0x02 爬楼梯0x03 三步问题0x04 使用最小花费爬楼梯⭐解法一解法二 0x05 解码方法* 四、总结与提炼 一、…...

超简单免费转换ape到flac
1. 安装最新版的ffmpeg 2. 安装cywin环境 3. 设置path到ffmpeg export PATH$PATH:"PATH/TO/FFMPEG/BIN" 4.到ape所在的目录,执行以下命令 find . -iname "*.ape" | while read line; do fb${line::-4}; fn"$fb.flac";echo ffm…...

JavaScript混淆加密
什么是JS混淆加密? JavaScript混淆加密是一种通过对源代码进行变换,使其变得难以理解和分析的技术。它的目标是增加攻击者破解代码的难度,同时保持代码的功能不受影响。混淆加密的目的是使代码难以逆向工程,从而防止攻击者窃取知…...
Java8特性-Lambda表达式
📕概述 在Java 8中引入了Lambda表达式作为一项重要的语言特性,可以堪称是一种语法糖。Lambda表达式使得以函数式编程的方式解决问题变得更加简洁和便捷。 Lambda表达式的语法如下: (parameters) -> expression (参数) -> {代码}其中&…...
通过Power Platform自定义D365CE业务需求 - 1. Microsoft Power Apps 简介
Microsoft Power Apps是一个趋势性的、无代码和无代码的商业应用程序开发平台,配有一套应用程序、服务和连接器。其数据平台为构建适合任何业务需求的自定义业务应用程序提供了快速开发环境。随着无代码、少代码应用程序开发的引入,任何人都可以快速构建低代码应用程序,并与…...
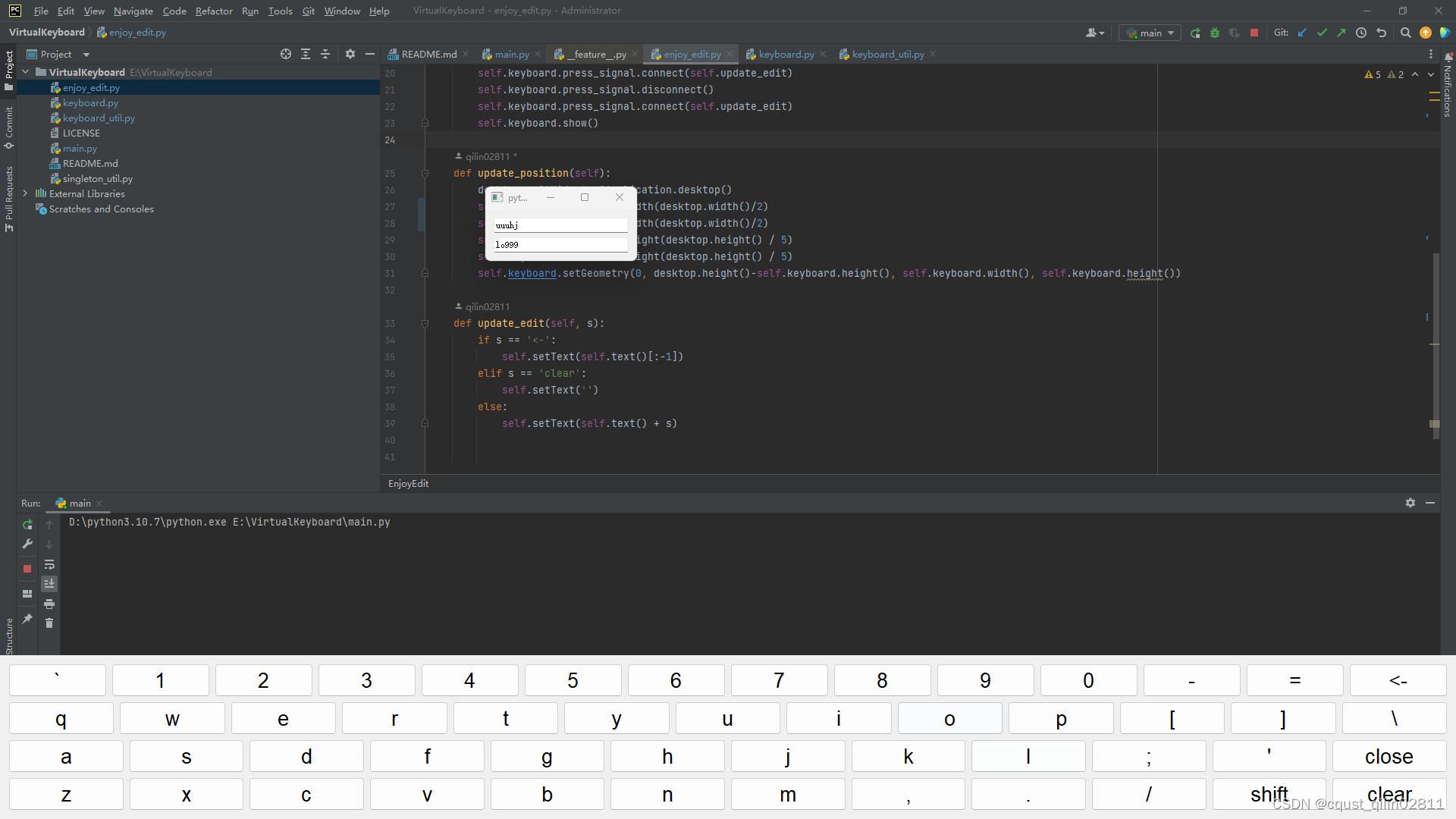
简易实现QT中的virtualkeyboard及问题总结
文章目录 前言:一、虚拟键盘的实现综合代码 二、为什么选用QWidget而不适用QDialog实现键盘三、从窗体a拉起窗体b后,窗体b闪退问题的探讨四、关闭主窗口时子窗口未关闭的问题 前言: 本文章主要包含四部分: 虚拟键盘的实现&#…...

景联文科技可为多模态语音翻译模型提供数据采集支持
8月22日Facebook的母公司Meta Platforms发布了一种能够翻译和转录数十种语言的人工智能模型——SeamlessM4T,可以在日常生活中或者商务交流中为用户提供更便捷的翻译和转录服务。 相较于传统的文本翻译,这项技术的最大区别在于它可以实现端到端的语音翻译…...

定时器分批请求数据
<!DOCTYPE html> <html><script>//需要分页的数组let arr [1,2,3,4,5,6,7,8,9,10]//分割数组,每页3条splitArr(arr,4)/*** 分割数组*/function splitArr(idList,size){//当前页数let num 1//共多少页let count Math.ceil(idList.length / siz…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
