【CS324】Large Language Models(持续更新)
note
文章目录
- note
- 一、引言
- 二、大模型的能力
- 三、大模型的有害性(上)
- 四、大模型的有害性(下)
- 五、大模型的数据
- Reference
一、引言
- 语言模型最初是在信息理论的背景下研究的,可以用来估计英语的熵。
- 熵用于度量概率分布: H ( p ) = ∑ x p ( x ) log 1 p ( x ) . H(p) = \sum_x p(x) \log \frac{1}{p(x)}. H(p)=x∑p(x)logp(x)1.
- 熵实际上是一个衡量将样本 x ∼ p x∼p x∼p 编码(即压缩)成比特串所需要的预期比特数的度量。举例来说,“the mouse ate the cheese” 可能会被编码成 “0001110101”。熵的值越小,表明序列的结构性越强,编码的长度就越短。直观地理解, log 1 p ( x ) \log \frac{1}{p(x)} logp(x)1 可以视为用于表示出现概率为 p ( x ) p(x) p(x)的元素 x x x的编码的长度。
- 交叉熵H(p,q)上界是熵H§: H ( p , q ) = ∑ x p ( x ) log 1 q ( x ) . H(p,q) = \sum_x p(x) \log \frac{1}{q(x)}. H(p,q)=x∑p(x)logq(x)1.,所以可以通过构建一个只有来自真实数据分布 p p p的样本的(语言)模型 q q q来估计 H ( p , q ) H(p,q) H(p,q)
- N-gram模型在计算上极其高效,但在统计上效率低下。
- 神经语言模型在统计上是高效的,但在计算上是低效的。
- 大模型的参数发展:随着深度学习在2010年代的兴起和主要硬件的进步(例如GPU),神经语言模型的规模已经大幅增加。以下表格显示,在过去4年中,模型的大小增加了5000倍。
| Model | Organization | Date | Size (# params) |
|---|---|---|---|
| ELMo | AI2 | Feb 2018 | 94,000,000 |
| GPT | OpenAI | Jun 2018 | 110,000,000 |
| BERT | Oct 2018 | 340,000,000 | |
| XLM | Jan 2019 | 655,000,000 | |
| GPT-2 | OpenAI | Mar 2019 | 1,500,000,000 |
| RoBERTa | Jul 2019 | 355,000,000 | |
| Megatron-LM | NVIDIA | Sep 2019 | 8,300,000,000 |
| T5 | Oct 2019 | 11,000,000,000 | |
| Turing-NLG | Microsoft | Feb 2020 | 17,000,000,000 |
| GPT-3 | OpenAI | May 2020 | 175,000,000,000 |
| Megatron-Turing NLG | Microsoft, NVIDIA | Oct 2021 | 530,000,000,000 |
| Gopher | DeepMind | Dec 2021 | 280,000,000,000 |
二、大模型的能力
三、大模型的有害性(上)
四、大模型的有害性(下)
五、大模型的数据
Reference
[1] 斯坦福大学CS324课程:https://stanford-cs324.github.io/winter2022/lectures/introduction/#a-brief-history
[2] CS224N lecture notes on language models
相关文章:
)
【CS324】Large Language Models(持续更新)
note 文章目录 note一、引言二、大模型的能力三、大模型的有害性(上)四、大模型的有害性(下)五、大模型的数据Reference 一、引言 语言模型最初是在信息理论的背景下研究的,可以用来估计英语的熵。 熵用于度量概率分布…...

【学习笔记】「2020-2021 集训队作业」Communication Network
有点难😅 发现容斥系数设计的非常巧妙🤔 设 f ( i ) f(i) f(i)表示恰好有 i i i条边相同的方案数, g ( i ) g(i) g(i)表示至少有 i i i条边相同的方案数 根据二项式反演, g ( i ) ∑ j ≥ i ( j i ) f ( j ) ⇒ f ( i ) ∑ j…...

文章参考链接
文章参考: 前端 echsrt横轴文字过长,…展示【link】js数组去重【link】js数据是String去重【link】js数据是对象去重【link】小程序使用wxml-to-canvas【link】vantui【link】微信小程序使用vantui组件【link】【link】微信小程序,选项卡页面…...
SQLI-labs-第七关
知识点:单引号()加括号闭合错误的布尔盲注 思路: 寻找注入点 我们首先看一下正常的回显,并没有显示出什么明显的信息 输入?id1 发现报错 输入?id1 -- 还是报错,说明SQL语句的语法错误可能不是单引号闭合…...

腾讯云轻量2核4G5M服务器_CPU内存_流量_带宽_系统盘
腾讯云轻量2核4G5M服务器:CPU内存流量带宽系统盘性能测评:轻量应用服务器2核4G5M带宽,免费500GB月流量,60GB系统盘SSD盘,5M带宽下载速度可达640KB/秒,流量超额按照0.8元每GB支付流量费,轻量2核4…...
从零开始搭建Apache服务器并使用内网穿透技术实现公网访问
Apache服务安装配置与结合内网穿透实现公网访问 文章目录 Apache服务安装配置与结合内网穿透实现公网访问前言1.Apache服务安装配置1.1 进入官网下载安装包1.2 Apache服务配置 2.安装cpolar内网穿透2.1 注册cpolar账号2.2 下载cpolar客户端 3. 获取远程桌面公网地址3.1 登录cpo…...

unordered_map和unordered_set的使用
前言 在C98中,STL提供了底层为红黑树的结构的一系列关联式容器,在查询时效率可以达到logN,即使最差的情况下需要比较红黑树的高度次,当树中的节点较多时,查询的效率也不是很理想,最好的查询是,进…...

javascript【格式化时间日期】
javascript【格式化时间日期】 操作: (1) 日期格式化代码 /*** 日期格式化函数<br/>* 调用格式:需要使用日期对象调用* <p> new Date().Format("yyyy/MM/dd HH:mm:ss"); </p>* param fmt 日期格式* returns {*} 返回格式化…...

CCC数字钥匙设计【NFC】--什么是AID?
1、NFC中的AID是什么? AID,英文全称为Application Identifier,这是NFC技术中的概念,AID用于唯一标识一个应用。 NFC应用的AID相关操作,包括注册和删除应用的AID、查询应用是否是指定AID的默认应用、获取应用的AID等 …...

变压器耐压试验电压及电源容量的计算
被试变压器的额定电压为(11081. 25%) /10. 5kV, 联接组标号为 YNd11。 试验时高压分接开关置于第 1 分接位置, 即高压侧电压为 126kV, 高、 低压电压比 K1126/(√310. 5) 6. 93。 现以 A 相试验…...

uniapp实现底部弹出菜单选择
其实uniapp有内置的组件,不用自己去实现,类似于这样: uni.showActionSheet({itemList: [菜单一, 菜单二, 菜单三],success: function (res) {console.log(选中了第${res.tapIndex 1}个菜单);},fail: function (res) {console.log(res.errMs…...

14. 线性代数 - 线性方程组
文章目录 线性方程组矩阵行列式全排列和逆序数N阶行列式(非)齐次线性方程Hi,大家好。我是茶桁。 结束了「微积分」部分的学习之后我们稍作休整,今天正式开始另外一部分:「线性代数」的学习。小伙伴们放松完回来要开始紧张起来了。 我们之前说过,不管是哪一个工程学科,根…...

C++QT day4
仿照string类,完成myString类 #include <iostream> #include <cstring> using namespace std; class myString {private:char *str; //记录c风格的字符串int size; //记录字符串的实际长度public://无参构造myString():size(10){s…...

Python中的 if __name__ ==‘main‘
你编写的程序迟早需要创建目录以便在其中存储数据。 os 和 pathlib 包含了创建目录的函数。我们将会考虑如下方法: | 方法 | 描述 | | -------------------- | -------------------------- | | os.mkdir() | 创建单个子目录 | | os.makedirs() | 创建多个目录&…...

github 创建自己的分支 并下载代码
github创建自己的分支 并下载代码 目录概述需求: 设计思路实现思路分析1.进入到master分支,git checkout master;2.master-slave的个人远程仓库3.爬虫调度器4.建立本地分支与个人远程分支之间的联系5.master 拓展实现 参考资料和推荐阅读 Survive by day…...

算法:贪心---跳一跳
1、题目: 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 2…...

机器学习入门教学——梯度下降、梯度上升
1、简介 梯度表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(梯度的方向)变化最快,变化率(梯度的模)最大,可理解为导数。梯度上升和梯度下降是优化算法中常用的…...
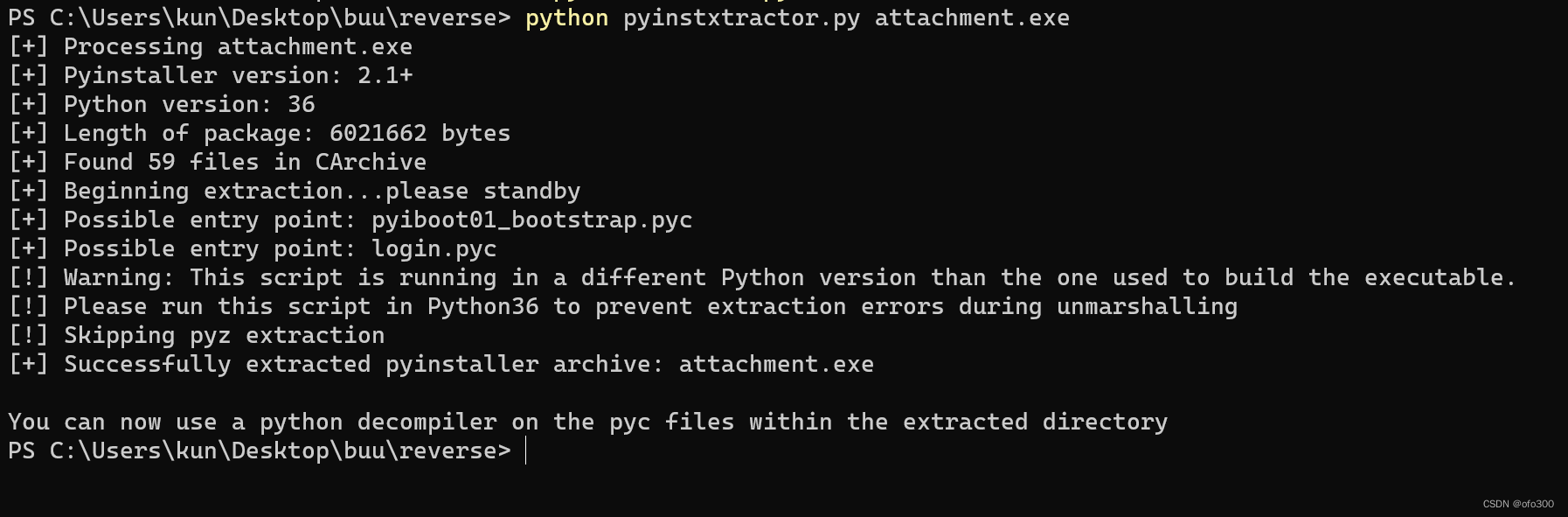
BUUCTF Reverse/[羊城杯 2020]login(python程序)
查看信息,python文件 动调了一下,该程序创建了一个线程来读入数据,而这个线程的代码应该是放在内存中直接执行的,本地看不到代码,很蛋疼 查了下可以用PyInstaller Extractor工具来解包,可以参考这个Python解包及反编译…...

indexDB localForage
一、前言 前端本地化存储算是一个老生常谈的话题了,我们对于 cookies、Web Storage(sessionStorage、localStorage)的使用已经非常熟悉,在面试与实际操作之中也会经常遇到相关的问题,但这些本地化存储的方式还存在一些…...

Spring Boot开发时Java对象和Json对象互转
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开兴好久好久😎 📚系列专栏:Java全栈,…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...

【Zephyr 系列 16】构建 BLE + LoRa 协同通信系统:网关转发与混合调度实战
🧠关键词:Zephyr、BLE、LoRa、混合通信、事件驱动、网关中继、低功耗调度 📌面向读者:希望将 BLE 和 LoRa 结合应用于资产追踪、环境监测、远程数据采集等场景的开发者 📊篇幅预计:5300+ 字 🧭 背景与需求 在许多 IoT 项目中,单一通信方式往往难以兼顾近场数据采集…...
