【学习笔记】「2020-2021 集训队作业」Communication Network
有点难😅
发现容斥系数设计的非常巧妙🤔
设 f ( i ) f(i) f(i)表示恰好有 i i i条边相同的方案数, g ( i ) g(i) g(i)表示至少有 i i i条边相同的方案数
根据二项式反演, g ( i ) = ∑ j ≥ i ( j i ) f ( j ) ⇒ f ( i ) = ∑ j ≥ i ( − 1 ) j − i ( j i ) g j g(i)=\sum_{j\ge i}\binom{j}{i}f(j)\Rightarrow f(i)=\sum_{j\ge i}(-1)^{j-i}\binom{j}{i}g_j g(i)=∑j≥i(ij)f(j)⇒f(i)=∑j≥i(−1)j−i(ij)gj
这个式子成立是因为 [ i = j ] = ∑ j ≤ k ≤ i ( − 1 ) k − j ( i k ) ( k j ) [i=j]=\sum_{j\le k\le i}(-1)^{k-j}\binom{i}{k}\binom{k}{j} [i=j]=∑j≤k≤i(−1)k−j(ki)(jk),点这里
用 g ( i ) g(i) g(i)进行替换,答案是 ∑ g ( j ) ⋅ ( ∑ i ≤ j i ⋅ 2 i ⋅ ( − 1 ) j − i ⋅ ( j i ) ) \sum g(j)\cdot (\sum_{i\le j}i\cdot 2^i\cdot (-1)^{j-i}\cdot \binom{j}{i}) ∑g(j)⋅(∑i≤ji⋅2i⋅(−1)j−i⋅(ij))
发现后面那一坨就等于 2 j 2j 2j。又根据 prufer \text{prufer} prufer序列,对于 k k k个连通块的生成树的方案数为 n k − 2 ∏ s i n^{k-2}\prod s_i nk−2∏si,可以转化为在每个连通块中钦定选一个点以及在选的边中钦定选一条边的方案数,这样就做完了。
类似的题目:CF1842G Tenzing and Random Operations
复杂度 O ( n ) O(n) O(n)。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define fi first
#define se second
#define db double
#define ull unsigned long long
#define inf 0x3f3f3f3f
using namespace std;
const int mod=998244353;
const int N=2e6+5;
int n;
ll dp[N][2][2];
vector<int>G[N];
ll fpow(ll x,ll y=mod-2){ll z(1);for(;y;y>>=1){if(y&1)z=z*x%mod;x=x*x%mod;}return z;
}
void add(ll &x,ll y){x=(x+y)%mod;
}
void dfs(int u,int topf){dp[u][0][0]=dp[u][1][0]=1;for(auto v:G[u]){if(v==topf)continue;dfs(v,u),memset(dp[0],0,sizeof dp[0]);for(int i=0;i<2;i++){for(int j=0;j<2;j++){for(int k=0;k<2;k++){for(int l=0;l<2;l++){if(j==1&&l==1)continue;if(i==0||k==0){add(dp[0][i+k][j+l],dp[u][i][j]*dp[v][k][l]);if(j==0&&l==0)add(dp[0][i+k][1],dp[u][i][j]*dp[v][k][l]);}if(k==1){add(dp[0][i][j+l],dp[u][i][j]*dp[v][k][l]%mod*n);}}}}}memcpy(dp[u],dp[0],sizeof dp[0]);}
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<n;i++){int x,y;cin>>x>>y;G[x].pb(y),G[y].pb(x);}dfs(1,0)ll res=dp[1][1][1]*fpow(n,mod-2)%mod*2%mod;cout<<(res+mod)%mod;
}
相关文章:

【学习笔记】「2020-2021 集训队作业」Communication Network
有点难😅 发现容斥系数设计的非常巧妙🤔 设 f ( i ) f(i) f(i)表示恰好有 i i i条边相同的方案数, g ( i ) g(i) g(i)表示至少有 i i i条边相同的方案数 根据二项式反演, g ( i ) ∑ j ≥ i ( j i ) f ( j ) ⇒ f ( i ) ∑ j…...

文章参考链接
文章参考: 前端 echsrt横轴文字过长,…展示【link】js数组去重【link】js数据是String去重【link】js数据是对象去重【link】小程序使用wxml-to-canvas【link】vantui【link】微信小程序使用vantui组件【link】【link】微信小程序,选项卡页面…...
SQLI-labs-第七关
知识点:单引号()加括号闭合错误的布尔盲注 思路: 寻找注入点 我们首先看一下正常的回显,并没有显示出什么明显的信息 输入?id1 发现报错 输入?id1 -- 还是报错,说明SQL语句的语法错误可能不是单引号闭合…...

腾讯云轻量2核4G5M服务器_CPU内存_流量_带宽_系统盘
腾讯云轻量2核4G5M服务器:CPU内存流量带宽系统盘性能测评:轻量应用服务器2核4G5M带宽,免费500GB月流量,60GB系统盘SSD盘,5M带宽下载速度可达640KB/秒,流量超额按照0.8元每GB支付流量费,轻量2核4…...
从零开始搭建Apache服务器并使用内网穿透技术实现公网访问
Apache服务安装配置与结合内网穿透实现公网访问 文章目录 Apache服务安装配置与结合内网穿透实现公网访问前言1.Apache服务安装配置1.1 进入官网下载安装包1.2 Apache服务配置 2.安装cpolar内网穿透2.1 注册cpolar账号2.2 下载cpolar客户端 3. 获取远程桌面公网地址3.1 登录cpo…...

unordered_map和unordered_set的使用
前言 在C98中,STL提供了底层为红黑树的结构的一系列关联式容器,在查询时效率可以达到logN,即使最差的情况下需要比较红黑树的高度次,当树中的节点较多时,查询的效率也不是很理想,最好的查询是,进…...

javascript【格式化时间日期】
javascript【格式化时间日期】 操作: (1) 日期格式化代码 /*** 日期格式化函数<br/>* 调用格式:需要使用日期对象调用* <p> new Date().Format("yyyy/MM/dd HH:mm:ss"); </p>* param fmt 日期格式* returns {*} 返回格式化…...

CCC数字钥匙设计【NFC】--什么是AID?
1、NFC中的AID是什么? AID,英文全称为Application Identifier,这是NFC技术中的概念,AID用于唯一标识一个应用。 NFC应用的AID相关操作,包括注册和删除应用的AID、查询应用是否是指定AID的默认应用、获取应用的AID等 …...

变压器耐压试验电压及电源容量的计算
被试变压器的额定电压为(11081. 25%) /10. 5kV, 联接组标号为 YNd11。 试验时高压分接开关置于第 1 分接位置, 即高压侧电压为 126kV, 高、 低压电压比 K1126/(√310. 5) 6. 93。 现以 A 相试验…...

uniapp实现底部弹出菜单选择
其实uniapp有内置的组件,不用自己去实现,类似于这样: uni.showActionSheet({itemList: [菜单一, 菜单二, 菜单三],success: function (res) {console.log(选中了第${res.tapIndex 1}个菜单);},fail: function (res) {console.log(res.errMs…...

14. 线性代数 - 线性方程组
文章目录 线性方程组矩阵行列式全排列和逆序数N阶行列式(非)齐次线性方程Hi,大家好。我是茶桁。 结束了「微积分」部分的学习之后我们稍作休整,今天正式开始另外一部分:「线性代数」的学习。小伙伴们放松完回来要开始紧张起来了。 我们之前说过,不管是哪一个工程学科,根…...

C++QT day4
仿照string类,完成myString类 #include <iostream> #include <cstring> using namespace std; class myString {private:char *str; //记录c风格的字符串int size; //记录字符串的实际长度public://无参构造myString():size(10){s…...

Python中的 if __name__ ==‘main‘
你编写的程序迟早需要创建目录以便在其中存储数据。 os 和 pathlib 包含了创建目录的函数。我们将会考虑如下方法: | 方法 | 描述 | | -------------------- | -------------------------- | | os.mkdir() | 创建单个子目录 | | os.makedirs() | 创建多个目录&…...

github 创建自己的分支 并下载代码
github创建自己的分支 并下载代码 目录概述需求: 设计思路实现思路分析1.进入到master分支,git checkout master;2.master-slave的个人远程仓库3.爬虫调度器4.建立本地分支与个人远程分支之间的联系5.master 拓展实现 参考资料和推荐阅读 Survive by day…...

算法:贪心---跳一跳
1、题目: 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 2…...

机器学习入门教学——梯度下降、梯度上升
1、简介 梯度表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(梯度的方向)变化最快,变化率(梯度的模)最大,可理解为导数。梯度上升和梯度下降是优化算法中常用的…...
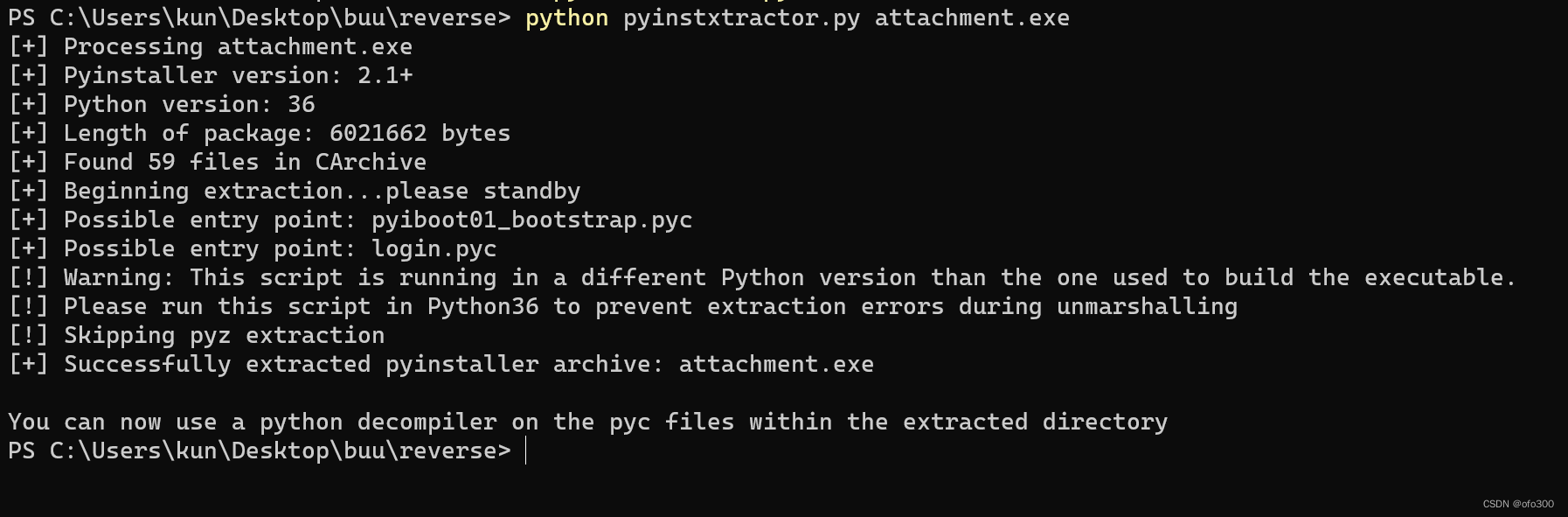
BUUCTF Reverse/[羊城杯 2020]login(python程序)
查看信息,python文件 动调了一下,该程序创建了一个线程来读入数据,而这个线程的代码应该是放在内存中直接执行的,本地看不到代码,很蛋疼 查了下可以用PyInstaller Extractor工具来解包,可以参考这个Python解包及反编译…...

indexDB localForage
一、前言 前端本地化存储算是一个老生常谈的话题了,我们对于 cookies、Web Storage(sessionStorage、localStorage)的使用已经非常熟悉,在面试与实际操作之中也会经常遇到相关的问题,但这些本地化存储的方式还存在一些…...

Spring Boot开发时Java对象和Json对象互转
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开兴好久好久😎 📚系列专栏:Java全栈,…...

C++ 多态
引例: #include<iostream> using namespace std; class Animal { public:void speak(){cout<<"动物在说话"<<endl;} }; class Cat:public Animal { public:void speak(){cout<<"小猫在说话"<<endl;} }; void Do…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...

多模态大语言模型arxiv论文略读(110)
CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文标题:CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文作者:Hidehisa Arai, Keita Miwa, Kento Sasaki, Yu Yamaguchi, …...
