当前位置： 首页 > news >正文

喜报丨迪捷软件入选浙江省2023年省级产业数字化服务商

news 2026/2/8 21:10:11

近日，根据《关于组织开展2023年度省级产业数字化服务商申报工作的通知》要求，省经信厅公布2023年省级产业数字化服务商名单，浙江迪捷软件科技有限公司榜上有名。

省级产业数字化服务商上榜名单的评选在企业申报、地方推荐、专家评审、综合评估等基础上进行，入围企业要求具有较强的经济实力、技术研发和融合创新能力，并已面向细分行业、工业企业提供服务且取得较好成效，在行业内具有一定的声誉和影响力,是为企业数字化转型提供专业工程技术服务的主要力量。

本次入选2023年省级产业数字化服务商名单，标志着迪捷软件在嵌入式DevOps、MBSE和数字装备产品及解决方案中领先的技术实力和服务能力获得了省经信厅的高度认可。

关于迪捷软件 

迪捷软件专注于安全关键领域数字化转型，遵循中立开放的商业理念，致力于核心工业软件国产化研究，攻关【卡脖子】技术，为我国安全关键领域提供嵌入式DevOps、MBSE和数字装备产品及解决方案，以构建全生命周期的数字孪生系统。

迪捷软件的创始团队和核心技术团队均来自清华大学计算机系的系统软件和软件工程研究所，在嵌入式虚拟化、形式化证明和符号执行等领域处于国内领先地位，发起的开源项目有SkyEye，L2C，Android_S2E等，俱在国内外有较高知名度。

经过近20年在研发和产品创新体系上的下沉和深耕，迪捷软件推出了自主创新、自主设计、自主可控、自主知识产权的一系列嵌入式DevOps与MBSE仿真建模产品：天目全数字实时仿真软件SkyEye、建模仿真与代码生成软件ModelCoder、多领域分布式协同仿真平台DigiThread，及嵌入式DevOps解决方案和数字样机解决方案，涉及了高端装备的需求、设计、开发直至仿真测试等环节，已成功应用于我国C919、飞机发动机、载人航天、火星探测器、核电站、汽车、轨交等领域，提供了基于计算机的高效设计开发环境，解决了高端装备软件开发和测试时硬件环境搭建成本高、资源调度难、研发周期长等问题，填补了国内嵌入式虚拟仿真领域空白。

▲迪捷软件三大产品和两大解决方案

相关文章：

喜报丨迪捷软件入选浙江省2023年省级产业数字化服务商

近日，根据《关于组织开展2023年度省级产业数字化服务商申报工作的通知》要求，省经信厅公布2023年省级产业数字化服务商名单，浙江迪捷软件科技有限公司榜上有名。 省级产业数字化服务商上榜名单的评选在企业申报、地方推荐、专家评审、综合评估…...

编程日记 2023/9/12 6:30:57

verilog写rom，采用端口排序顺序例化

verilog写rom，采用端口排序顺序例化 1，介绍rom，以及rom与ram的区别2，RTL设计模块、门级网表以及testbench测试模块2.1 RTL设计2.2 门级网表2.3 testbench3，波形输出1，介绍rom，以及rom与ram的区别 参考文献： 1, 转载-ROM、RAM存储器原理详解以及DRAM、SRAM、SDRAM 、FLA…...

编程日记 2023/9/12 6:29:56

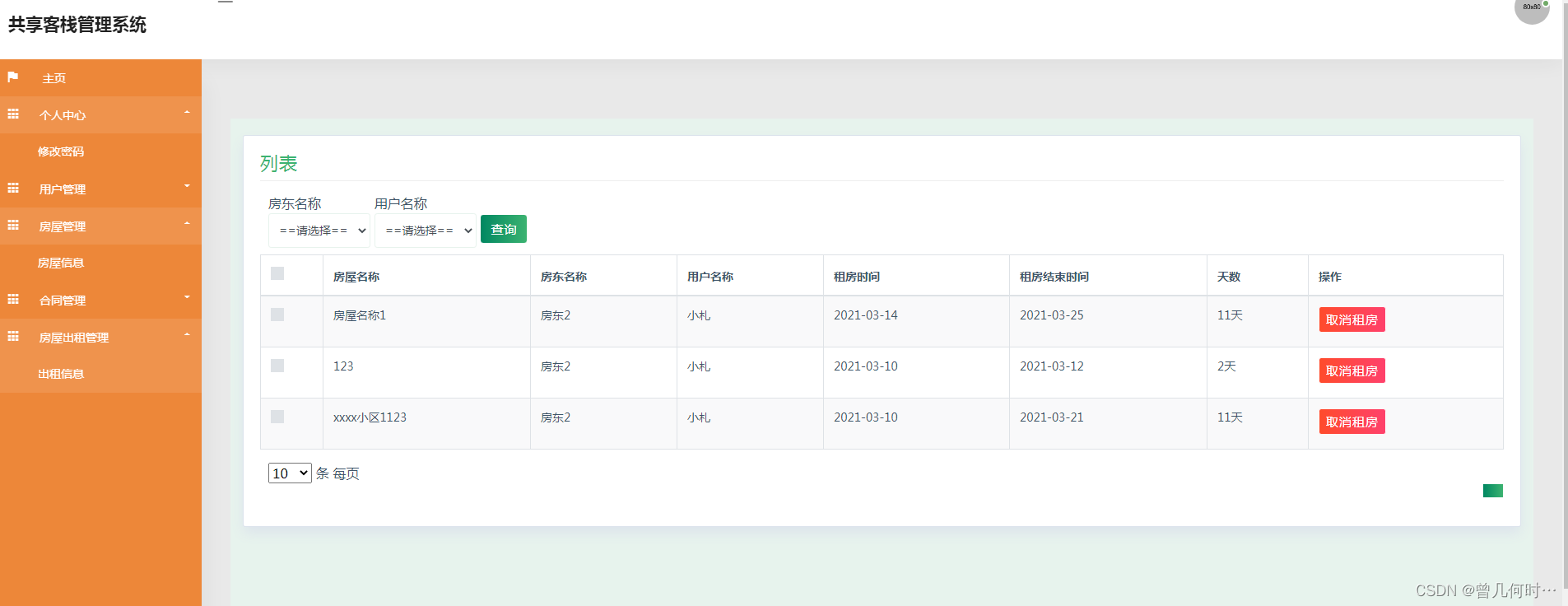
基于SSM的共享客栈管理系统的设计与实现

末尾获取源码 开发语言：Java Java开发工具：JDK1.8 后端框架：SSM 前端：采用JSP技术开发 数据库：MySQL5.7和Navicat管理工具结合 服务器：Tomcat8.5 开发软件：IDEA / Eclipse 是否Maven项目&#x…...

编程日记 2023/9/12 6:28:56

全屏Activity弹出键盘不顶起布局

最近遇到的一个问题是全屏Activity中要求弹出键盘不顶起布局，首先windowSoftInputMode的取值是有多个的，在全屏场景下adjustPan是没有用的，需要使用adjustResize首先确保键盘不顶起布局。 android:windowSoftInputMode"stateHidden|adju…...

编程日记 2023/9/12 6:27:54

JAVA设计模式详解 解构设计模式思想 详细代码对比

JAVA设计模式详解 1 简单工厂模式 1 简单工厂模式 设计模式-01简单工厂模式详解 详细代码对比...

编程日记 2023/9/12 6:26:54

lintcode 567 · 最大得分 【动态规划 中等 】

题目 https://www.lintcode.com/problem/567 给定一个矩阵matrix， matrix[i][j]表示你到达第i行第j列可以得到的分数，现在你要用第0行任意一点出发，从每行里找到一个点进行跳跃，每次从(i,j)到(i1,k)跳跃需要消耗∣j−k∣的分数&…...

编程日记 2023/9/12 6:25:52

qml嵌入到QWidget的两种方式介绍

本文介绍qml页面嵌入到QWidget的两种方式，以及这两种方式的区别。 方式1 在 Qt 中，可以使用 QQuickWidget 将 QML 内容嵌入到基于 QWidget 的应用程序中。这是在旧的 QWidget-based 应用程序中逐渐引入 QML UI 的一种常见方式。 以下是如何使用 QQuickWidget 将 QML 内容嵌…...

编程日记 2023/9/12 6:24:50

Mysql数据库之常用SQL语句及事务学习总结

数据库介绍 几个常见的缩写： DB：数据库。全称：DataBase。DBMS：数据库管理系统。全称：DataBase Management System。DBS：数据库系统。全称：DataBase System。DBA：数据库管理员。全称…...

编程日记 2023/9/12 6:23:49

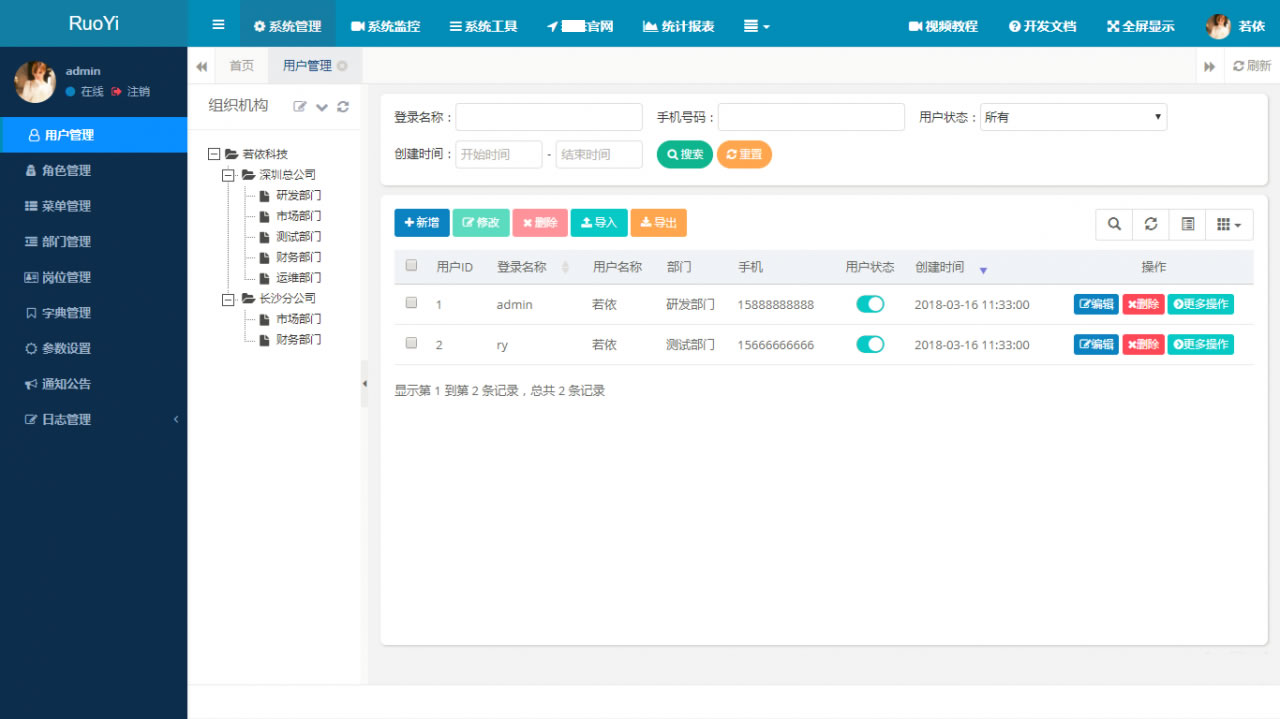
RuoYi若依管理系统最新版 基于SpringBoot的权限管理系统

RuoYi是一个后台管理系统，基于经典技术组合（Spring Boot、Apache Shiro、MyBatis、Thymeleaf）主要目的让开发者注重专注业务，降低技术难度，从而节省人力成本，缩短项目周期，提高软件安全质量。 本…...

编程日记 2023/9/12 6:22:48

html实现邮件模版布局-flex布局table布局-demo

邮件模版布局 flex - 布局简单方便 兼容性差 table - 优点 就是兼容性好&#xff0c;其他没有优点 注&#xff1a;使用图片需要png最好&#xff0c;使用svg图google邮箱会出现不能使用的情况 效果图 flex布局 <!DOCTYPE html> <html lang"en" xmlns:th&qu…...

编程日记 2023/9/12 6:21:47

CENTOS7安装redis在/home/pms/software路径下，并且将redis加入到systemctl中

要将/home/software/redis-stack-server-7.2.0-v0/service/redis.service添加到systemctl系统管理&#xff0c;你可以执行以下步骤&#xff1a; 创建软连接&#xff1a; sudo ln -s /home/software/redis-stack-server-7.2.0-v0/service/redis.service /etc/systemd/system/r…...

编程日记 2023/9/12 6:20:46

数据库笔记

数据库原理及应用 半期考&#xff1a;运筹学&#xff0c;概率论&#xff0c;数据库 文章目录 数据库原理及应用1.课程的考核2.数据库的运用3.数据库学什么&#xff1f; 第一章 绪论1.1数据库系统概述1.1.1基本概念1.1.2数据管理技术的生产和发展人工管理文件系统数据库系统 1.…...

编程日记 2023/9/12 6:19:45

AI是风口还是泡沫？

KlipC报道&#xff1a;狂热的人工智能追捧潮有所冷静&#xff0c;投资者在“上头”的追涨之后&#xff0c;开始回归到对基本面的关注。 KlipC的合伙人Andi D表示&#xff1a;“近日&#xff0c;有关英伟达二季度“破纪录”财报涉嫌造假的话题正在社交媒体和投资者论坛中甚嚣尘上…...

编程日记 2023/9/12 6:18:44

echarts环图配置

echarts环图配置 1、安装echarts npm install echarts4.9.02、页面引入echarts import echarts from echarts;3、应用 template片段 <div class"chart-wrap"><div id "treeChart" style "width: 180px; height:180px;" ><…...

编程日记 2023/9/12 6:17:43

Redis优化 RDB AOF持久化

---------------------- Redis 高可用 ---------------------------------------- 在web服务器中&#xff0c;高可用是指服务器可以正常访问的时间&#xff0c;衡量的标准是在多长时间内可以提供正常服务&#xff08;99.9%、99.99%、99.999%等等&#xff09;。 但是在Redis语境…...

编程日记 2023/9/12 6:16:42

三维模型3DTILE格式轻量化压缩主要技术方法浅析

三维模型3DTILE格式轻量化压缩主要技术方法浅析 三维模型3DTILE格式轻量化压缩主要技术方法浅析 随着三维地理空间数据的应用日益广泛&#xff0c;为了更快速地传输和存储这些大规模数据&#xff0c;3DTile格式的轻量化压缩显得尤为重要。本文将浅析关于三维模型3DTile格式轻量…...

编程日记 2023/9/12 6:15:41

c++day2---9.7

1> 思维导图 2> 封装一个结构体&#xff0c;结构体中包含一个私有数组&#xff0c;用来存放学生的成绩&#xff0c;包含一个私有变量&#xff0c;用来记录学生个数&#xff0c; 提供一个公有成员函数&#xff0c;void setNum(int num)用于设置学生个数 提供一个公有成员…...

编程日记 2023/9/12 6:14:39

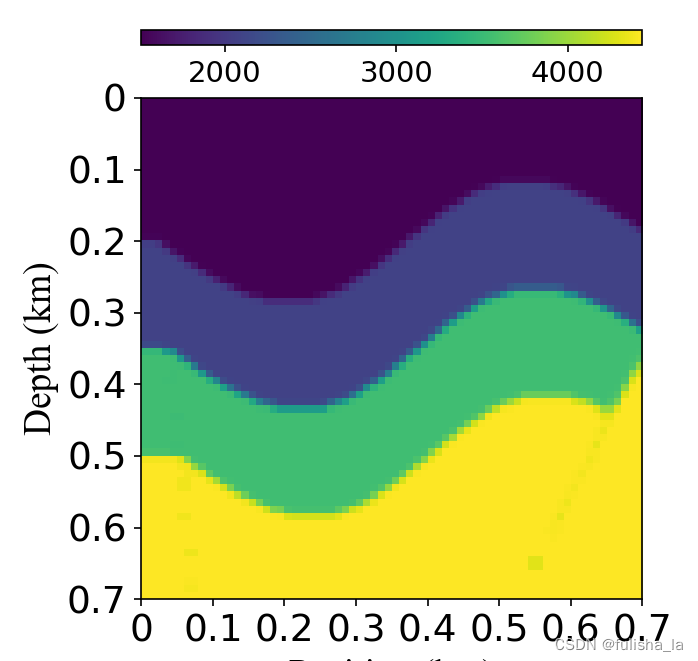
地震反演基础知识2(代码演示)

文章目录 数据集代码演示1. SEG盐真实数据2. SEG盐速度模型3. SEG盐模拟地震数据4. SEG盐模拟速度模型5. openfwi地震数据6. openfwi速度模型 数据集代码演示 1. SEG盐真实数据 # 绘制SEG盐层数据的地震图像 def pain_seg_seismic_data(para_seismic_data):Plotting seismic …...

编程日记 2023/9/12 6:13:37

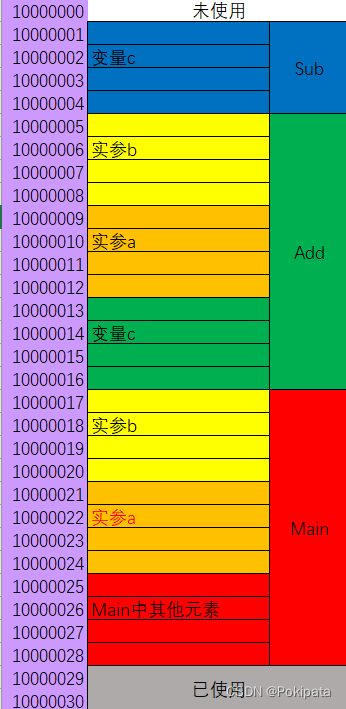
C#学习 - 方法的定义、调用、调试

方法 方法&#xff08;Method&#xff09;是由C/C中的函数&#xff08;Function&#xff09;发展而来的 //C语言 #include <stdio.h> int Add(int x, int y) {return x y; }//函数 int main(void) {int a 4;int b 2;int c Add(a, b);printf("%d %d %d\n&quo…...

编程日记 2023/9/12 6:12:36

『PyQt5-Qt Designer篇』｜ 09 Qt Designer中分割线和间隔如何使用？

09 Qt Designer中分割线和间隔如何使用？ 1 间隔1.1 水平间隔1.2 垂直间隔2 分割线2.1 水平线2.2 垂直线3 保存并执行1 间隔 间隔有水平间隔和垂直间隔： 1.1 水平间隔 拖动4个按钮，并设置为水平布局： 在第一个按钮的右边添加一个水平间隔： 设置其sizeType为Fixed，宽度为20…...

编程日记 2023/9/12 6:11:35

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密

在实际项目中，用户注册、登录、修改密码等操作，都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输，在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

编程新知 2025/11/28 6:00:25

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力

引言&#xff1a; 在人工智能快速发展的浪潮中&#xff0c;快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型&#xff08;LLM&#xff09;。该模型代表着该领域的重大突破&#xff0c;通过独特方式融合思考与非思考…...

编程新知 2026/2/6 19:29:20

IT供电系统绝缘监测及故障定位解决方案

随着新能源的快速发展&#xff0c;光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域&#xff0c;IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选&#xff0c;但在长期运行中&#xff0c;例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

编程新知 2026/2/1 6:36:36

Device Mapper 机制

Device Mapper 机制详解 Device Mapper&#xff08;简称 DM&#xff09;是 Linux 内核中的一套通用块设备映射框架&#xff0c;为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程&#xff0c;并配以详细的…...

编程新知 2025/12/14 13:11:33

现有的 Redis 分布式锁库（如 Redisson）提供了哪些便利？

现有的 Redis 分布式锁库&#xff08;如 Redisson&#xff09;相比于开发者自己基于 Redis 命令&#xff08;如 SETNX, EXPIRE, DEL&#xff09;手动实现分布式锁&#xff0c;提供了巨大的便利性和健壮性。主要体现在以下几个方面&#xff1a; 原子性保证 (Atomicity)&#xff…...

编程新知 2025/9/23 11:26:04

五子棋测试用例

一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏&#xff0c;有着深厚的文化底蕴。通过将五子棋制作成网页游戏&#xff0c;可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家&#xff0c;都可以通过网页五子棋感受到东方棋类…...

编程新知 2026/2/1 21:56:50

macOS 终端智能代理检测

&#x1f9e0; 终端智能代理检测&#xff1a;自动判断是否需要设置代理访问 GitHub 在开发中&#xff0c;使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新&#xff0c;例如&#xff1a; fatal: unable to access https://github.com/ohmyzsh/oh…...

编程新知 2026/1/22 15:34:33

WEB3全栈开发——面试专业技能点P4数据库

一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库&#xff0c;基于 mysql 库改进而来&#xff0c;具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点&#xff1a; 支持 Promise / async-await&#xf…...

编程新知 2025/8/17 13:47:50

STM32标准库-ADC数模转换器

文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”&#xff1a;输入模块&#xff08;GPIO、温度、V_REFINT&#xff09;1.4.2 信号 “调度站”&#xff1a;多路开关1.4.3 信号 “加工厂”&#xff1a;ADC 转换器&#xff08;规则组 注入…...

编程新知 2026/2/1 22:00:58

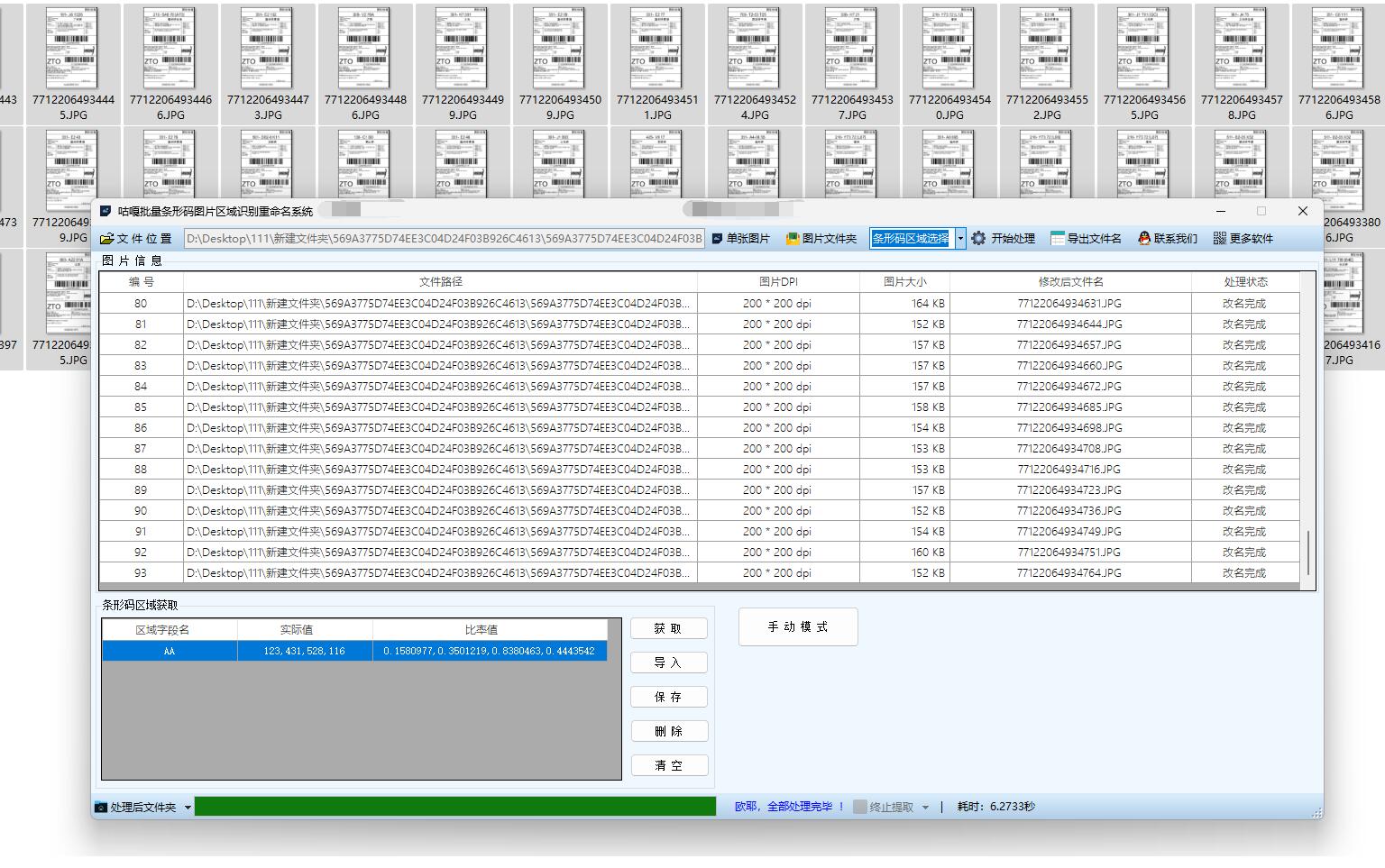
【工具教程】多个条形码识别用条码内容对图片重命名，批量PDF条形码识别后用条码内容批量改名，使用教程及注意事项

一、条形码识别改名使用教程 打开软件并选择处理模式&#xff1a;打开软件后&#xff0c;根据要处理的文件类型&#xff0c;选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件&#xff0c;就选择 “PDF 识别模式”&#xff1b;若是处理图片文件&…...

编程新知 2026/2/4 16:24:31