C++数据结构--红黑树
目录
- 一、红黑树的概念
- 二、红黑树的性质
- 三、红黑树的节点的定义
- 四、红黑树结构
- 五、红黑树的插入操作
- 参考代码
- 五、代码汇总
一、红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路
径会比其他路径长出俩倍,因而是接近平衡的。如图所示:

二、红黑树的性质
- 每个结点不是红色就是黑色。
- 根节点是黑色的。
- 如果一个节点是红色的,则它的两个孩子结点是黑色的。
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点。
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)。
问题:为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍?
因为根节点是黑色是固定的,并且不能有连续的红色节点,每条路径黑色节点的个数一样,也就是说最短路就是全黑,最长路径就是一黑一红相间,所以一条路径的红色节点要么和黑色节点一样多,要么少于黑色节点,即同一条路径黑色节点的占比是大于等于50%的,所以最长路径一定不超过最短路径的2倍。
三、红黑树的节点的定义
//通过枚举定义红色和黑色的常量enum Colour{RED,BLACK};template <class K,class V>struct RBTreeNode{public://红黑树存放的值pair<K, V> _kv;//节点的三叉链指针RBTreeNode<K,V>* _left;RBTreeNode<K,V>* _right;RBTreeNode<K,V>* _parent;//节点的颜色Colour _col;//构造函数RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}};
思考:在节点的定义中,为什么要将节点的默认颜色给成红色的?
这个问题就是关于插入节点的时候我们默认插入的是黑色的节点还是红色的节点了,根据红黑树的规则,每一条路径的黑色节点的个数是一样的,假如我们插入黑色节点,那么某条路径的黑色节点就多了一个,也就是说其它路径的黑色节点也要增加一个,但是我们只插入了一个节点,要令其它路径的黑色节点的数量都增加一个,这个操作的难度显然是很大的,但是如果我们默认插入一个红色节点,那么我们最多违反了根节点为黑色或者连续两个红色节点的规则,主要还是容易违反连续两个红色节点的规则,这个问题只会影响当前节点到祖先这条路径,不会影响其他路径的节点,所以处理起来会更简洁一些,所以我们默认插入的节点是红色的。
四、红黑树结构

五、红黑树的插入操作
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
- 按照二叉搜索树的规则插入新节点。
- 检测新节点插入后,红黑树的性质是否遭到破坏,如果是,就要通过变色加旋转操作维持红黑树的性质。
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点。
情况一: cur为红,p为红,g为黑,u存在且为红。
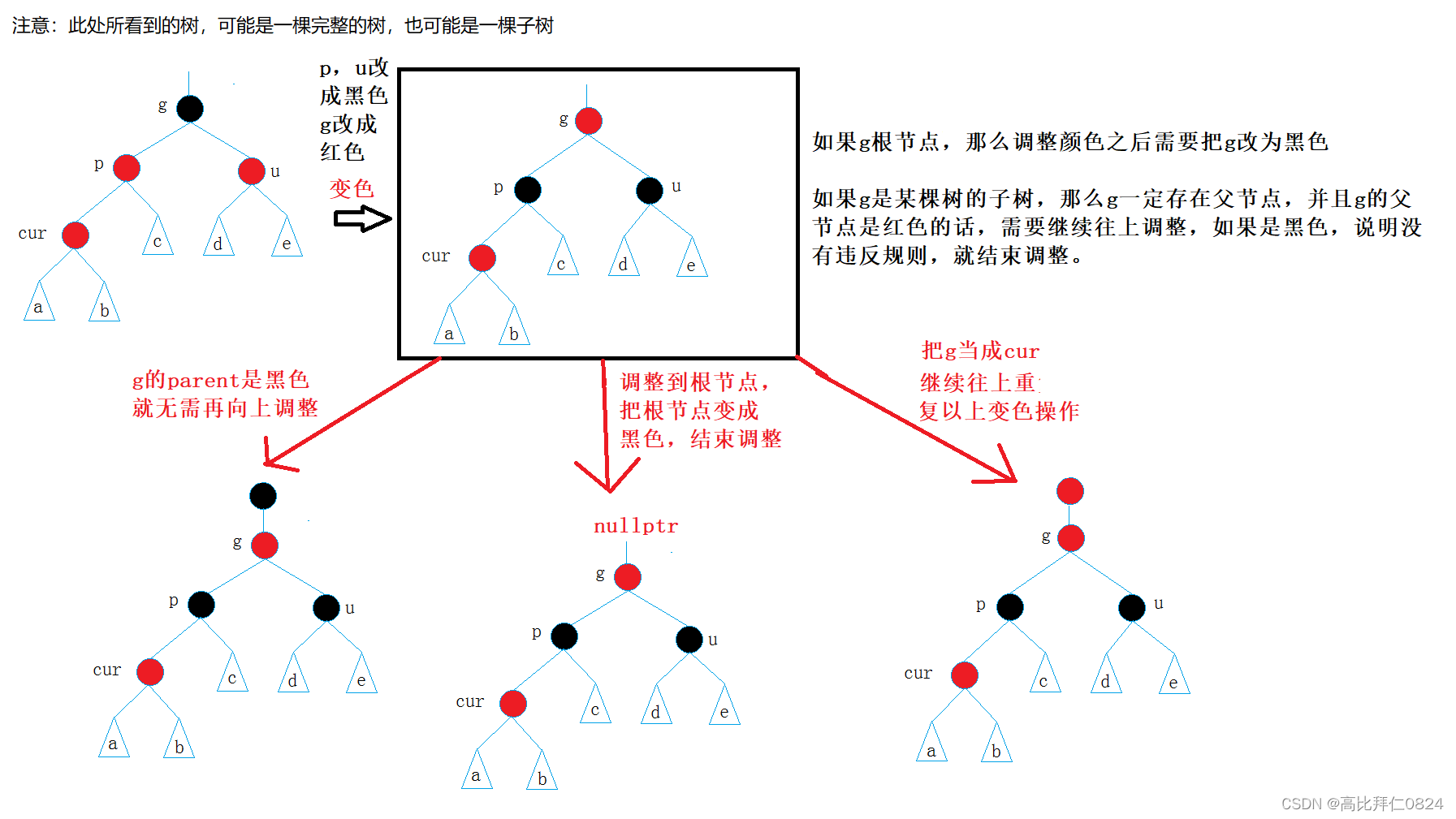
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑。
因为旋转后需要把p变成黑色,所以p节点和p的父节点不能再出现连续两个红色节点,所以旋转+变色后就不用再沿祖先路径更新了。

情况一:

情况二:

情况三:

情况四:

参考代码
bool Insert(const pair<K, V>& kv){//如果是空树,那么就直接插入一个黑色节点做根即可//注意要改颜色,因为节点的颜色默认是红色的if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//根据二叉搜索树的规则插入节点,同时记录父节点Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;cur->_parent = parent;}else if (kv.first > parent->_kv.first){parent->_right = cur;cur->_parent = parent;}//走到这里已经插入完成,后面是检查新插入的节点有没有破坏红黑树的规则的逻辑//检查新插入的节点是否满足红黑树的规则,如果不满足就要进行变色/变色+旋转//因为新插入的cur节点的颜色一定是红色的,当cur的父节点存在并且为红色//时说明出现了连续的两个红色节点,这时需要进行变色/变色+旋转,如果父节点// 不存在或者存在且为黑色时就无需再处理了。// 为什么父节点有可能不存在?因为这是一个循环,循环更新往祖先处理可能到达根节点,//到了根节点就无需再处理了while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (cur == parent->_left){// grandfather// parent//cur//画图//叔叔存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续沿祖先路径检查cur = grandfather;parent = cur->_parent;//这里曾经漏写了}//叔叔不存在或者存在且为黑else//(uncle==nullptr||uncle->_col==BLACK){//单纯的左边高,进行右单旋+变色RotateR(grandfather);grandfather->_col = RED;parent->_col = BLACK;//旋转完之后无需再沿祖先路径处理break;}}else//cur == parent->_right{// grandfather// parent// cur//画图//叔叔存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续往上调整cur = grandfather;parent = cur->_parent;//这里曾经忘记写}//叔叔不存在或者存在且为黑else//(uncle==nullptr || uncle->_col == BLACK){//左右双旋RotateL(parent);RotateR(grandfather);//变色grandfather->_col = RED;cur->_col = BLACK;//旋转后就无需再沿祖先路径检查了,具体原因画图理解break;}}}else//(parent == grandfather->_right){Node* uncle = grandfather->_left;if (cur == parent->_right){// grandfather// parent// cur//画图//叔叔存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续沿祖先路径检查cur = grandfather;parent = cur->_parent;}//叔叔不存在或者存在且为黑else//(uncle==nullptr || uncle->_col == BLACK){//单纯的右边高,进行左单旋+变色RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;//旋转+变色后就不需要再沿祖先路径检查了break;}}else//(cur == parent->_left){// grandfather// parent// cur//叔叔存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续沿祖先路径检查cur = grandfather;parent = cur->_parent;}//叔叔不存在或者存在且为黑else//(uncle==nullptr || uncle->_col == BLACK){//根据模型可知需要右左双旋+变色RotateR(parent);RotateL(grandfather);grandfather->_col = RED;cur->_col = BLACK;//旋转后就不需要再沿祖先路径检查了break;}}}}_num++;//最后记得把根节点的颜色改成黑色_root->_col = BLACK;return true;}//旋转的细节如果不清楚的话请看上一篇关于AVL树的旋转,红黑树的旋转和AVL树的旋转是一样的void RotateL(Node* parent){assert(parent);Node* cur = parent->_right;Node* curleft = cur->_left;Node* parentParent = parent->_parent;parent->_right = curleft;cur->_left = parent;if (curleft){curleft->_parent = parent;}parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = cur;}else{parentParent->_right = cur;}cur->_parent = parentParent;}}void RotateR(Node* parent){assert(parent);Node* cur = parent->_left;Node* curright = cur->_right;Node* parentParent = parent->_parent;parent->_left = curright;cur->_right = parent;if (curright){curright->_parent = parent;}parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = cur;}else{parentParent->_right = cur;}cur->_parent = parentParent;}}
五、代码汇总
#pragma once#include <iostream>
using namespace std;
#include <assert.h>namespace kb
{enum Colour{RED,BLACK};template <class K,class V>struct RBTreeNode{public://红黑树存放的值pair<K, V> _kv;//节点的三叉链指针RBTreeNode<K,V>* _left;RBTreeNode<K,V>* _right;RBTreeNode<K,V>* _parent;//节点的颜色Colour _col;//构造函数RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}};template <class K,class V>class RBTree{typedef RBTreeNode<K, V> Node;public:bool Insert(const pair<K, V>& kv){//如果是空树,那么就直接插入一个黑色节点做根即可//注意要改颜色,因为节点的颜色默认是红色的if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//根据二叉搜索树的规则插入节点,同时记录父节点Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;cur->_parent = parent;}else if (kv.first > parent->_kv.first){parent->_right = cur;cur->_parent = parent;}//走到这里已经插入完成,后面是检查新插入的节点有没有破坏红黑树的规则的逻辑//检查新插入的节点是否满足红黑树的规则,如果不满足就要进行变色/变色+旋转//因为新插入的cur节点的颜色一定是红色的,当cur的父节点存在并且为红色//时说明出现了连续的两个红色节点,这时需要进行变色/变色+旋转,如果父节点// 不存在或者存在且为黑色时就无需再处理了。// 为什么父节点有可能不存在?因为这是一个循环,循环更新往祖先处理可能到达根节点,//到了根节点就无需再处理了while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (cur == parent->_left){// grandfather// parent//cur//画图//叔叔存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续沿祖先路径检查cur = grandfather;parent = cur->_parent;//这里曾经漏写了}//叔叔不存在或者存在且为黑else//(uncle==nullptr||uncle->_col==BLACK){//单纯的左边高,进行右单旋+变色RotateR(grandfather);grandfather->_col = RED;parent->_col = BLACK;//旋转完之后无需再沿祖先路径处理break;}}else//cur == parent->_right{// grandfather// parent// cur//画图//叔叔存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续往上调整cur = grandfather;parent = cur->_parent;//这里曾经忘记写}//叔叔不存在或者存在且为黑else//(uncle==nullptr || uncle->_col == BLACK){//左右双旋RotateL(parent);RotateR(grandfather);//变色grandfather->_col = RED;cur->_col = BLACK;//旋转后就无需再沿祖先路径检查了,具体原因画图理解break;}}}else//(parent == grandfather->_right){Node* uncle = grandfather->_left;if (cur == parent->_right){// grandfather// parent// cur//画图//叔叔存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续沿祖先路径检查cur = grandfather;parent = cur->_parent;}//叔叔不存在或者存在且为黑else//(uncle==nullptr || uncle->_col == BLACK){//单纯的右边高,进行左单旋+变色RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;//旋转+变色后就不需要再沿祖先路径检查了break;}}else//(cur == parent->_left){// grandfather// parent// cur//叔叔存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//继续沿祖先路径检查cur = grandfather;parent = cur->_parent;}//叔叔不存在或者存在且为黑else//(uncle==nullptr || uncle->_col == BLACK){//根据模型可知需要右左双旋+变色RotateR(parent);RotateL(grandfather);grandfather->_col = RED;cur->_col = BLACK;//旋转后就不需要再沿祖先路径检查了break;}}}}_num++;//最后记得把根节点的颜色改成黑色_root->_col = BLACK;return true;}size_t Size(){return _num;}bool Isbalance(){return _Isbalance(_root);}void Inorder(){_Inorder(_root);}private:bool CheckColour(Node* root, int blackNum, int BenchMark){//走到空树说明这条路径已经走完了,需要检查黑色节点的个数和基准值相不相等if (root == nullptr){//如果不相等,证明不平衡,返回falseif (blackNum != BenchMark){return false;}//如果相等,则说明本条路径没有出事,还要检查其它路径return true;}//如果出现连续红色节点证明这棵树出问题了,返回falseif (root->_col == RED && root->_parent && root->_parent->_col == RED){return false;}if (root->_col == BLACK){blackNum++;}//递归检查所有路径的颜色return CheckColour(root->_left, blackNum, BenchMark)&& CheckColour(root->_right, blackNum, BenchMark);}bool _Isbalance(Node* root){//空树可以认为是平衡的if (root == nullptr){return true;}//根节点不是黑色说明这棵树出事了if (root->_col != BLACK){return false;}//先算出一条路径的黑色节点的个数作为基准值,检查其它路径的黑色节点数目是否跟这个标准值//是否一样,如果不一样就证明这棵树不平衡了,那么如果这个基准值本身就是错的呢,那也没有关系,//只要有路径的黑色节点和其它路径不相等,就说明肯定有其中一条路径出问题了,至于是哪条路径//出问题就不重要了int BenchMark = 0;Node* cur = root;while (cur){if (cur->_col == BLACK){BenchMark++;}cur = cur->_left;}//检查所有路径中是否有连续红色节点和各路径中黑色节点的数目是否相等return CheckColour(root, 0, BenchMark);}void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_kv.second << " ";_Inorder(root->_right);}//旋转的细节如果不清楚的话请看上一篇关于AVL树的旋转,红黑树的旋转和AVL树的旋转是一样的void RotateL(Node* parent){assert(parent);Node* cur = parent->_right;Node* curleft = cur->_left;Node* parentParent = parent->_parent;parent->_right = curleft;cur->_left = parent;if (curleft){curleft->_parent = parent;}parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = cur;}else{parentParent->_right = cur;}cur->_parent = parentParent;}}void RotateR(Node* parent){assert(parent);Node* cur = parent->_left;Node* curright = cur->_right;Node* parentParent = parent->_parent;parent->_left = curright;cur->_right = parent;if (curright){curright->_parent = parent;}parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = cur;}else{parentParent->_right = cur;}cur->_parent = parentParent;}}private:Node* _root = nullptr;int _num = 0;//统计树的节点个数};void testRBTree(void){RBTree<int, int> rbt;int arr[]= { 16, 3, 7, 11, 9, 26, 18, 14, 15 };for (const auto& e : arr){rbt.Insert(make_pair(e, e));}/*rbt.Inorder();*/cout << rbt.Size() << endl;bool ret = rbt.Isbalance();cout << ret << endl;cout << endl;}void testRBTree1(void){RBTree<int, int> rbt;int N = 10000;srand((unsigned int)time(nullptr));for (size_t i=0;i<N;i++){int e = rand();rbt.Insert(make_pair(e, e));}cout << rbt.Size() << endl;bool ret = rbt.Isbalance();cout << ret << endl;cout << "插入完成" << endl;}
}
以上就是红黑树的相关内容了,最重要的是要理解当红黑树插入元素后违反了红黑树的规则时该如何对节点进行旋转加变色来使这棵红黑树重新回到平衡的。至于删除节点的操作就不实现了,有兴趣的可以去看看《算法导论》这本书,里面有讲红黑树删除操作的。
好啦,以上就是今天想要跟大家谈的关于红黑树的最重要的内容了,你学会了吗?如果你感觉到有所帮助,那么点点小心心,点点关注呗,后期还会持续更新C++的相关知识哦,我们下期见啦!!!
相关文章:

C++数据结构--红黑树
目录 一、红黑树的概念二、红黑树的性质三、红黑树的节点的定义四、红黑树结构五、红黑树的插入操作参考代码 五、代码汇总 一、红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过…...

Linux perf使用思考
目录 一、参考资料(建议阅读)二、值得思考的几个问题1、perf使用不同的性能事件进行统计有什么区别呢?2、那使用不同的性能事件统计出来的数据?排序是如何决定的,其中的百分比数值在不同的性能事件进行统计时各自的意义…...

自定义路由断言工厂
我们来设定一个场景: 假设我们的应用仅仅让age在(min,max)之间的人来访问。 第1步:在配置文件中,添加一个Age的断言配置 spring: application:name: api-gateway cloud:nacos:discovery:server-addr: 127.0.0.1:8848gateway:discovery:locator:enabled: trueroute…...
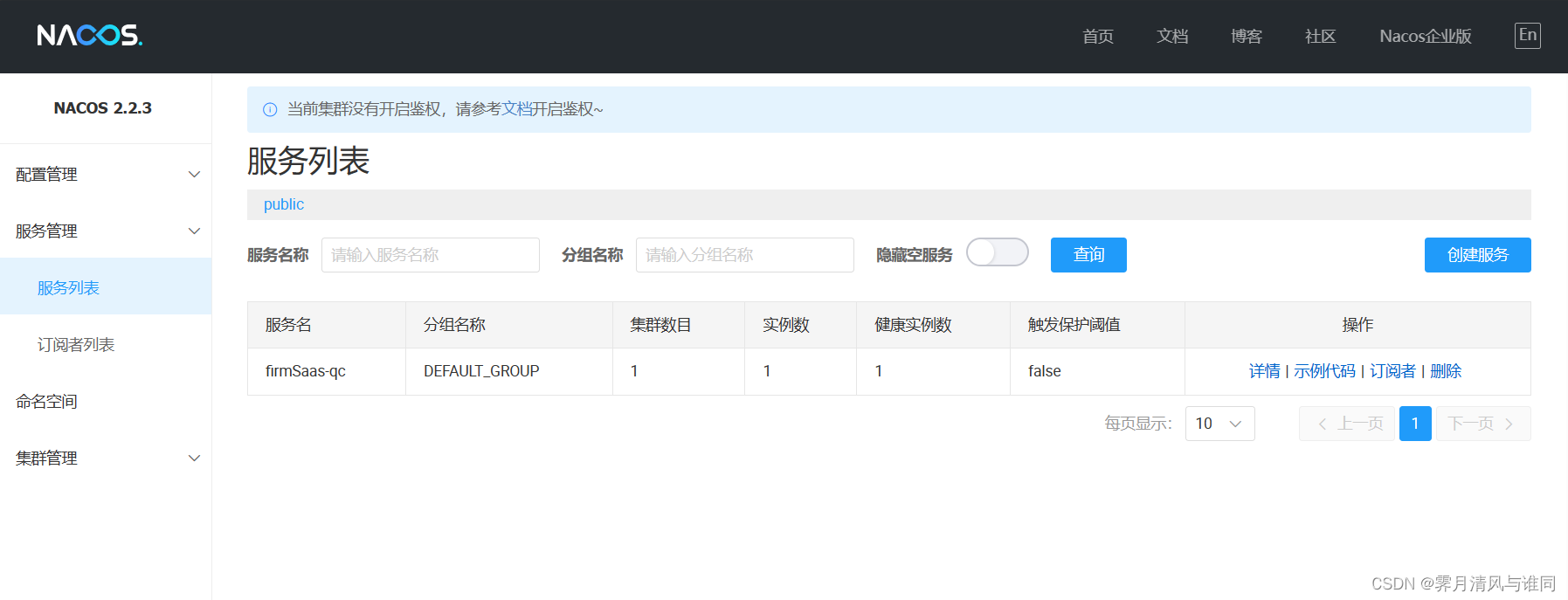
Nacos安装及在项目中的使用
目录 概要一、安装 Nacos1、下载 Nacos2、解压3、启动 Nacos 服务器4、自定义Nacos启动脚本5、访问Nacos Web控制台 二、Nacos----服务注册与发现1、添加 Nacos 依赖2、配置 Nacos 服务器地址3、使用 Nacos 注册服务4、启动服务 三、Nacos----配置管理1、创建配置数据2、从 Nac…...

overleaf中latex语法总结
α和bata $\alpha$ $\beta$上标和下标同时使用 $A_{IJ}^{IJ}$\\ %上标^下标_多个使用{}行内公式 \noindent $abc$\\ %行内公式\documentclass{article} \usepackage[utf8]{inputenc} \usepackage[namelimits]{amsmath} %数学公式 \usepackage{amssymb} %数学公式…...
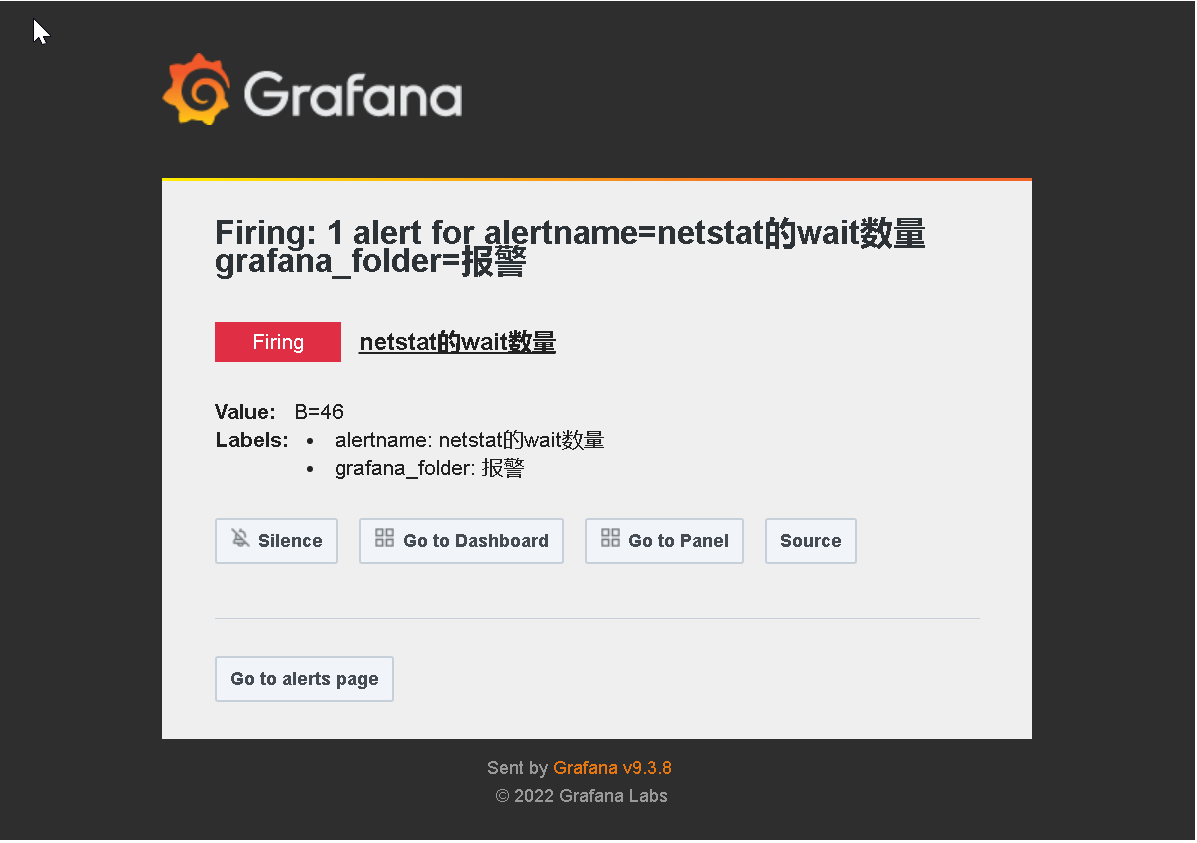
Grafana配置邮件告警
1、创建一个监控图 2、grafana邮件配置 vim /etc/grafana/grafana.ini [smtp] enabled true host smtp.163.com:465 user qinziteng05163.com password xxxxx # 授权码 from_address qinziteng05163.com from_name Grafanasystemctl restart grafana-serv…...

setup中的nextTick函数
await nextTick() 是 Vue 3 的一个异步函数,用于等待 DOM 更新完成后执行回调函数, 它在 setup 函数中非常有用,可以确保在对 DOM 进行操作之前,先等待 Vue 完成相关的 DOM 更新。 下面是一个示例,演示了 await nextT…...
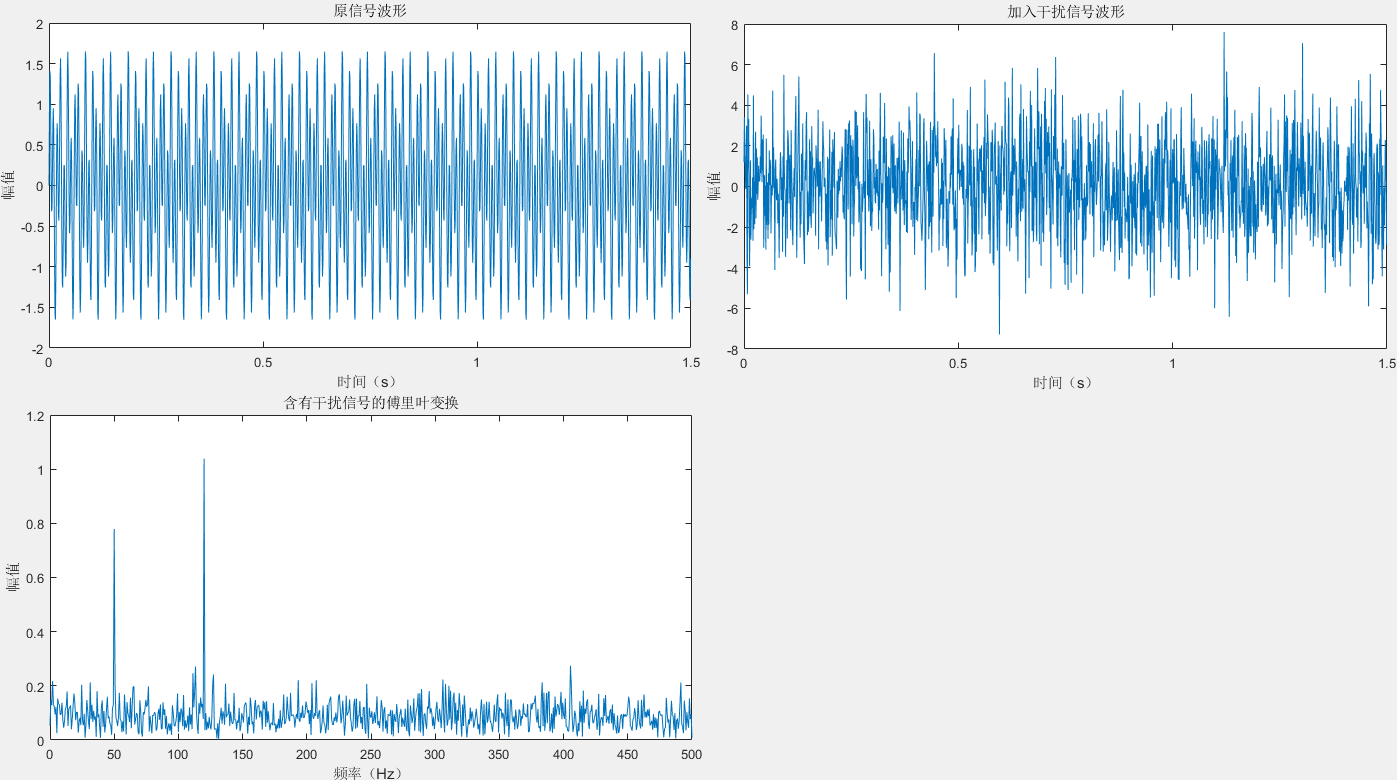
Matlab信号处理3:fft(快速傅里叶变换)标准使用方式
Fs 1000; % 采样频率 T 1/Fs; % 采样周期:0.001s L 1500; % 信号长度 t (0:L-1)*T; % 时间向量. 时间向量从0开始递增,0s~1.499sS 0.7*sin(2*pi*50*t) sin(2*pi*120*t); % 模拟原信号 X S 2*randn(size(t)); …...

Python|合并两个字典的几种方法
在Python中,有多种方法可以通过使用各种函数和构造函数来合并字典。在本文中,我们将讨论一些合并字典的方法。 1. 使用方法update() 通过使用Python中的update()方法,可以将一个列表合并到另一个列表中。但是在这种情况下,第二个…...

ElementUI浅尝辄止24:Message 消息提示
常用于主动操作后的反馈提示。与 Notification 的区别是后者更多用于系统级通知的被动提醒。 1.如何使用? Message 在配置上与 Notification 非常类似,所以部分 options 在此不做详尽解释,可以结合 Notification 的文档理解它们。Element 注…...

让照片动起来的软件,轻松制作照片动效
随着社交媒体的日益普及,我们对于照片的要求也越来越高。普通的照片已经不能满足我们的需求,我们希望照片更加生动有趣。照片动效便应运而生,它可以让照片动起来,吸引更多的注意力,让照片更加生动有趣。 照片动效制作起…...

【图解RabbitMQ-7】图解RabbitMQ五种队列模型(简单模型、工作模型、发布订阅模型、路由模型、主题模型)及代码实现
🧑💻作者名称:DaenCode 🎤作者简介:CSDN实力新星,后端开发两年经验,曾担任甲方技术代表,业余独自创办智源恩创网络科技工作室。会点点Java相关技术栈、帆软报表、低代码平台快速开…...

Linux命令200例:write用于向特定用户或特定终端发送信息
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌。CSDN专家博主,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师࿰…...
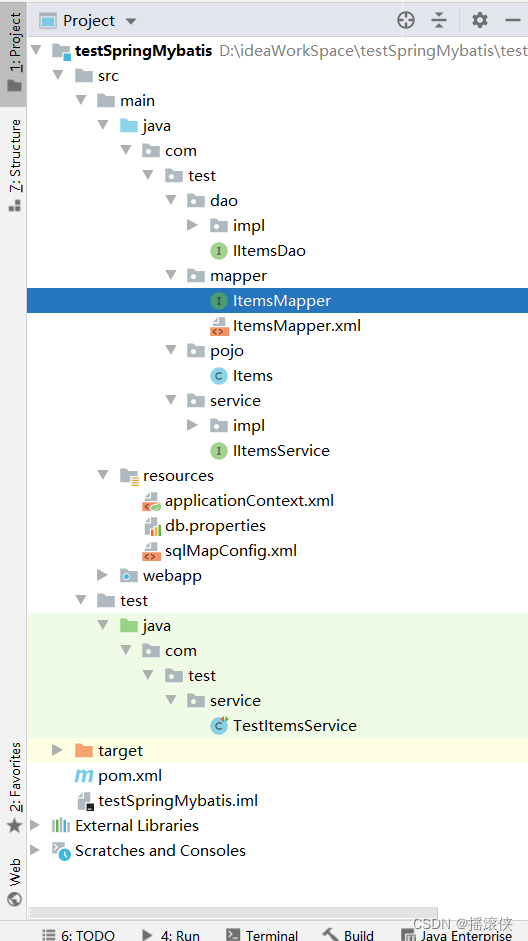
javaee spring整合mybatis spring帮我们创建dao层
项目结构 pom依赖 <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/P…...
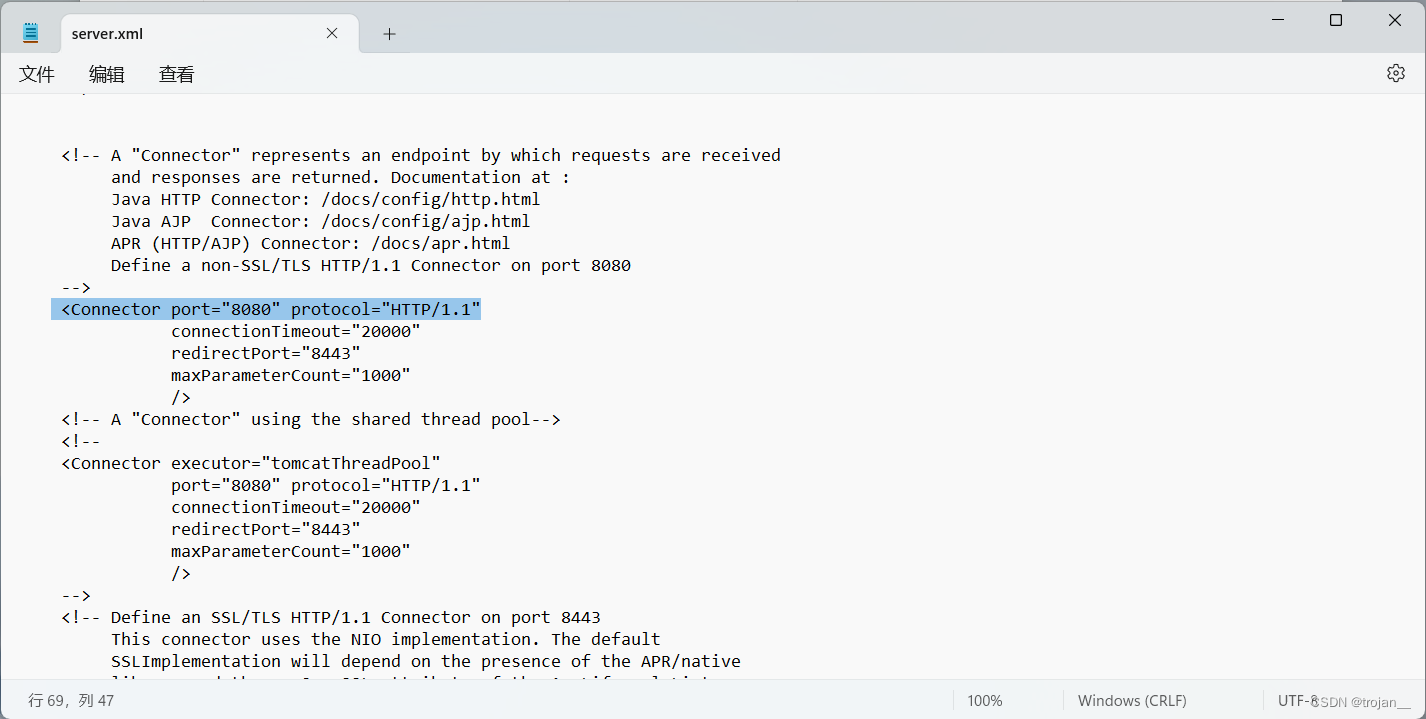
修改Tomcat的默认端口号
1、找到Tomcat的安装路径。 2、打开conf文件夹。 3、用记事本打开server.xml文件 4、找到 <Connector port"8080" protocol"HTTP/1.1",其中的8080就是tomcat的默认端口,将其修改为你需要的端口即可。...

Open3D Ransac拟合空间直线(python详细过程版)
RANSAC拟合直线 一、算法原理1、算法简介2、参考文献二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、算法原理 1、算法简介 见:Open3D——RANSAC 三维点云空间直线拟合 2、参考文献...

题目:2729.判断一个数是否迷人
题目来源: leetcode题目,网址:2729. 判断一个数是否迷人 - 力扣(LeetCode) 解题思路: 对 n,2*n,3*n 中的数字出现次数计数,若数字 0 出现 0 次,数字 1~9…...
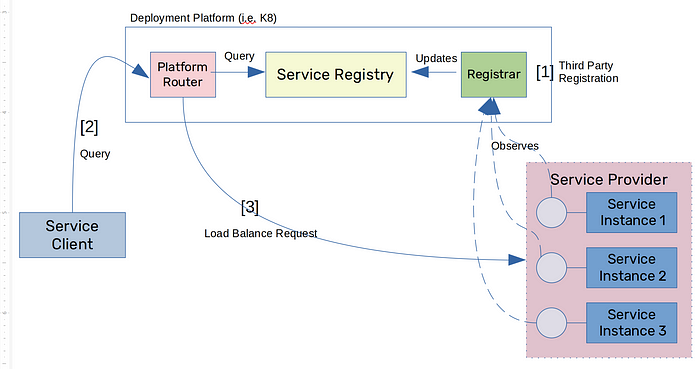
微服务模式:服务发现模式
由于微服务应用的动态性,很难调用具有固定 IP 地址的服务。这就是服务发现的概念出现的背景。服务发现有助于客户端了解服务实例的位置。在这种情况下,服务发现组件将充当服务注册表。 服务注册表是一个包含服务实例位置的集中式服务器/数据库。在微服务…...
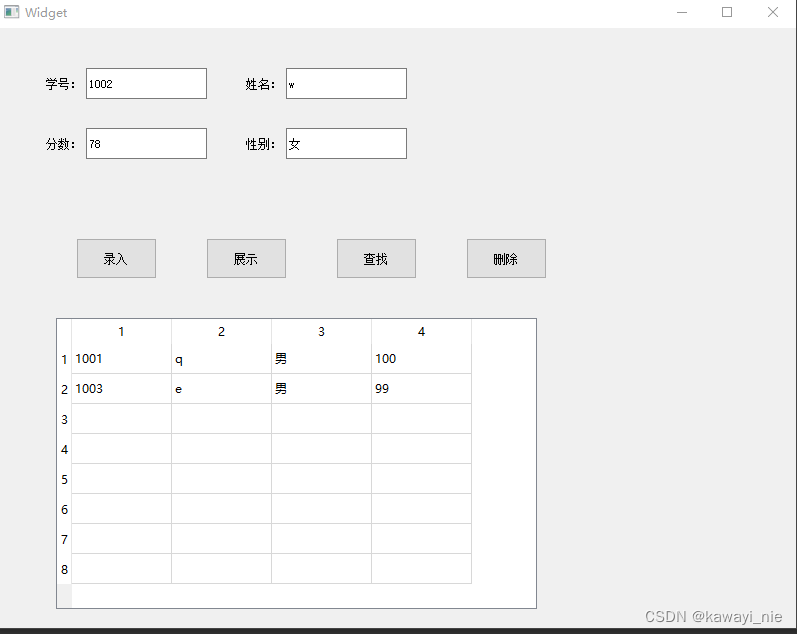
9.4 数据库 TCP
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//判断数据库对象是否包含了自己使用的数据库if(!db.contains("Stu.db")){//不存在数据库࿰…...
普通用户使用spark的client无法更新Ranger策略
普通用户使用spark的client无法更新Ranger策略 报错图片: WARN org.apache.ranger.admin.client.RangerAdminRESTClient: Error getting Roles. secureModetrue, usercaojianxiangUCDIPA.VIATRIS.CC (auth:KERBEROS),responsef"httpStatusCode&quo…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...
