LeetCode 88. 合并两个有序数组
文章目录
- 一、题目
- 二、C# 题解
一、题目
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
点击此处跳转题目。
示例 1:
输入: nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出: [1,2,2,3,5,6]
解释: 需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入: nums1 = [1], m = 1, nums2 = [], n = 0
输出: [1]
解释: 需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入: nums1 = [0], m = 0, nums2 = [1], n = 1
输出: [1]
解释: 需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
二、C# 题解
非常优雅的几行代码hh,很简单的题目了:
public class Solution {public void Merge(int[] nums1, int m, int[] nums2, int n) {int i = m - 1, j = n - 1, k = m + n - 1;while (i >= 0 && j >= 0) nums1[k--] = nums1[i] > nums2[j] ? nums1[i--] : nums2[j--];while (j >= 0) nums1[k--] = nums2[j--];return;}
}
- 时间复杂度: O ( m + n ) O(m+n) O(m+n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
相关文章:

LeetCode 88. 合并两个有序数组
文章目录 一、题目二、C# 题解 一、题目 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意&a…...
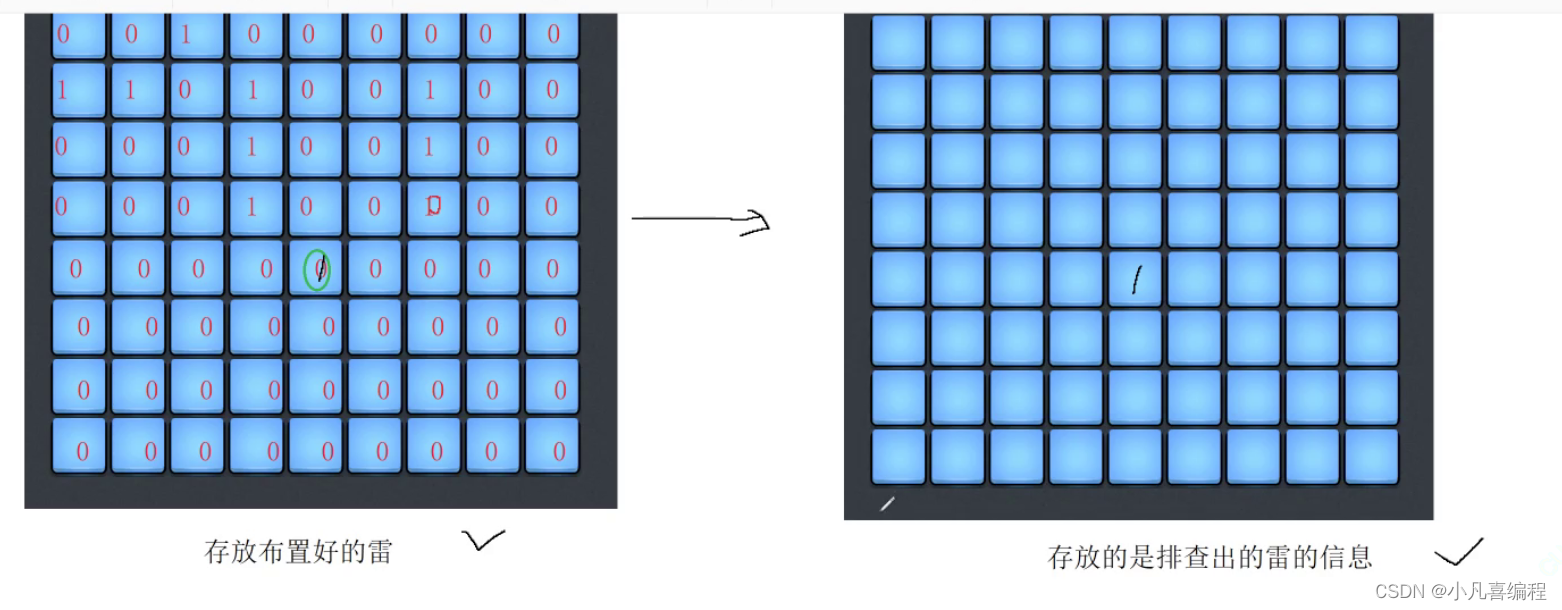
C语言实现扫雷小游戏
1.首先扫雷游戏要存储布置好的雷信息,需要一个二维数组 不是雷放* 雷:# 不是雷:0 雷:1 2. 给2个二维数组 9*9 一个存放雷的信息,一个存放布置好雷的信息 3.为了防止在统计坐标周围的…...
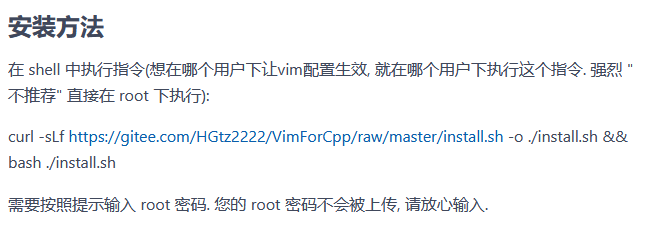
【linux基础(五)】Linux中的开发工具(上)---yum和vim
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:Linux从入门到开通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学更多操作系统知识 🔝🔝 Linux中的开发工具 1. 前言2.…...

C++学习之list的实现
在了解学习list实现之前我们首先了解一下关于迭代器的分类: 按功能分类: 正向迭代器 反向迭代器 const正向迭代器 const反向迭代器 按性质分类: 单向迭代器 只能 例如单链表 双向迭代器 可,也可-- 例如双…...

一种高效且节约内存的聚合数据结构的实现
一种高效且节约内存的聚合数据结构的实现 在特定的场景中,特殊定制数据结构能够得到更加好的性能且更节约内存。 聚合函数GroupArray的问题 GroupArray聚合函数是将分组内容组成一个个数组,例如下面的例子: SELECT groupArray(concat(ABC…...

机器学习(10)---特征选择
文章目录 一、概述二、Filter过滤法2.1 过滤法说明2.2 方差过滤2.3 方差过滤对模型影响 三、相关性过滤3.1 卡方过滤3.2 F检验3.3 互信息法3.4 过滤法总结 四、Embedded嵌入法4.1 嵌入法说明4.2 以随机森林为例的嵌入法 五、Wrapper包装法5.1 包装法说明5.2 以随机森林为例的包…...

Python之数据库(MYSQL)连接
一)数据库SQL语言基础 MySQL是一个关系型数据库管理系统,由瑞典MySQL AB 公司开发,目前属于 Oracle 旗下产品。MySQL 是最流行的关系型数据库管理系统之一,在 WEB 应用方面,MySQL是最好的 RDBMS (Relational Database…...
【建站教程】使用阿里云服务器怎么搭建网站?
使用阿里云服务器快速搭建网站教程,先为云服务器安装宝塔面板,然后在宝塔面板上新建站点,阿里云服务器网以搭建WordPress网站博客为例,阿小云来详细说下从阿里云服务器CPU内存配置选择、Web环境、域名解析到网站上线全流程&#x…...

【自然语言处理】关系抽取 —— MPDD 讲解
MPDD 论文信息 标题:MPDD: A Multi-Party Dialogue Dataset for Analysis of Emotions and Interpersonal Relationships 作者:Yi-Ting Chen, Hen-Hsen Huang, Hsin-Hsi Chen 期刊:LREC 2020 发布时间与更新时间:2020 主题:自然语言处理、关系抽取、对话场景、情感预测 数…...

深入理解JVM虚拟机第三篇:JVM的指令集架构模型和JVM的生命周期
文章目录 一:JVM的指令集架构模型 1:基于栈式架构的特点...

[小尾巴 UI 组件库] 组件库配置与使用
文章归档于:https://www.yuque.com/u27599042/row3c6 组件库地址 npm:https://www.npmjs.com/package/xwb-ui?activeTabreadme小尾巴 UI 组件库源码 gitee:https://gitee.com/tongchaowei/xwb-ui小尾巴 UI 组件库测试代码 gitee:…...
函数的理解)
Linux系统中fork()函数的理解
fork() 函数是一个在Unix和类Unix操作系统中常见的系统调用,用于创建一个新的进程,该进程是调用进程(父进程)的副本。fork() 函数的工作原理如下: 1. 当父进程调用 fork() 时,操作系统会创建一个新的进程&a…...
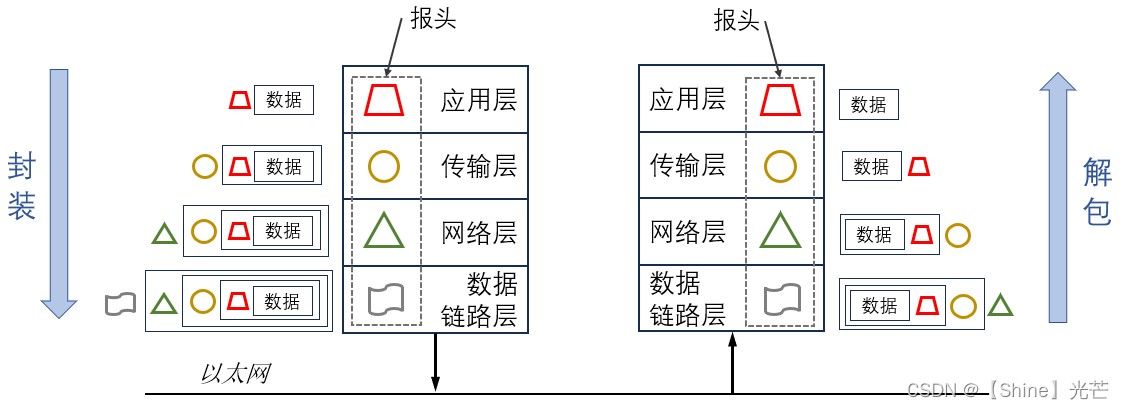
Linux网络编程:网络协议及网络传输的基本流程
目录 一. 计算机网络的发展 二. 网络协议的认识 2.1 对于协议分层的理解 2.2 TCP/IP五层协议模型 2.3 OSI七层模型 三. 网络传输的流程 3.1 同一网段中计算机通信的流程 3.2 不同网段中计算机设备的通信 3.3 对于IP地址和MAC地址的理解 3.4 数据的封装和解包 四. 总结…...

【大数据之Kafka】十、Kafka消费者工作流程
1 Kafka消费方式 (1)pull(拉)模式:消费者从broker中主动拉取数据。(Kafka中使用) 不足:如果Kafka中没有数据,消费者可能会陷入循环,一直返回空数据。 &#…...

如何确保ChatGPT的文本生成对特定行业术语的正确使用?
确保ChatGPT在特定行业术语的正确使用是一个重要而复杂的任务。这涉及到许多方面,包括数据预处理、模型训练、微调、评估和监控。下面我将详细介绍如何确保ChatGPT的文本生成对特定行业术语的正确使用,并探讨这一过程中的关键考虑因素。 ### 1. 数据预处…...
行业追踪,2023-09-11
自动复盘 2023-09-11 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...
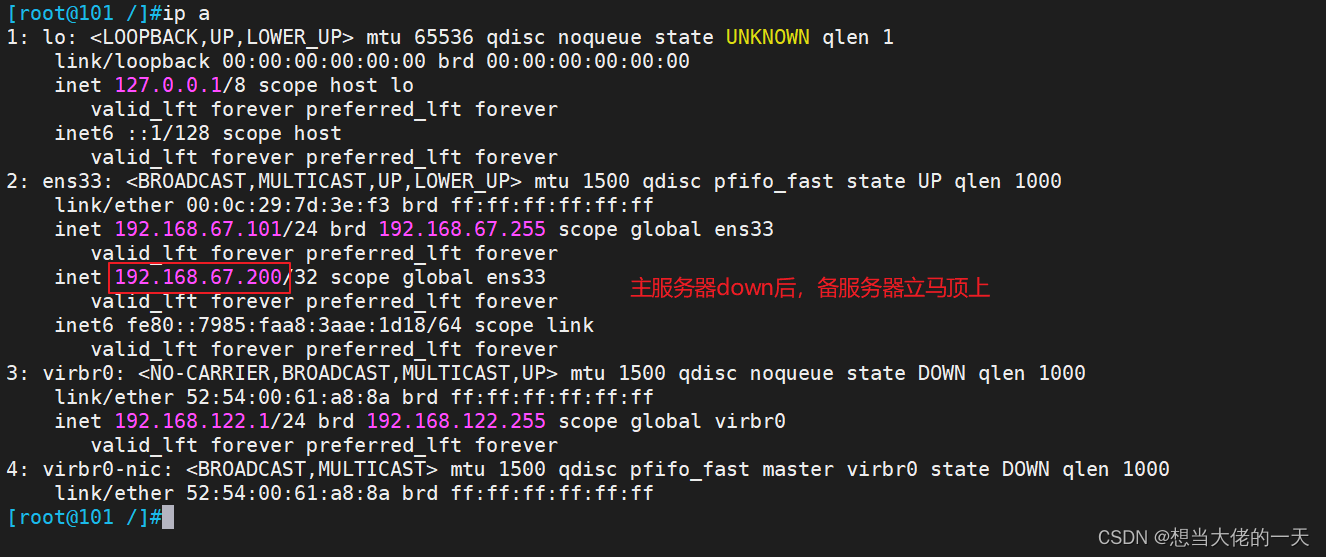
LVS + Keepalived群集
文章目录 1. Keepalived工具概述1.1 什么是Keepalived1.2 工作原理1.3 Keepailved实现原理1.4 Keepalived体系主要模块及其作用1.5 keepalived的抢占与非抢占模式 2. 脑裂现象 (拓展)2.1 什么是脑裂2.2 脑裂的产生原因2.3 如何解决脑裂2.4 如何预防脑裂 …...

springboot将jar改成war
一、maven项目 1、修改pom文件 <packaging>war</packaging>2、添加Servlet API依赖,Spring Boot的Starter依赖通常会包含这个依赖,所以你可能已经有了,没有就需要添加 <dependency><groupId>javax.servlet</gr…...

从9.10拼多多笔试第四题产生的01背包感悟
文章目录 题面基本的01背包问题本题变式 本文参考: 9.10拼多多笔试ak_牛客网 (nowcoder.com) 拼多多 秋招 2023.09.10 编程题目与题解 (xiaohongshu.com) 题面 拼多多9.10笔试的最后一题,是一道比较好的01背包变式问题,可以学习其解法加深对…...
搭建自己的OCR服务,第一步:选择合适的开源OCR项目
一、OCR是什么? 光学字符识别(Optical Character Recognition, OCR)是指对文本资料的图像文件进行分析识别处理,获取文字及版面信息的过程。 亦即将图像中的文字进行识别,并以文本的形式返回。 二、OCR的基本流程 1…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
