OpenCV(三十六):霍夫直线检测
1.检测直线的霍夫变换原理
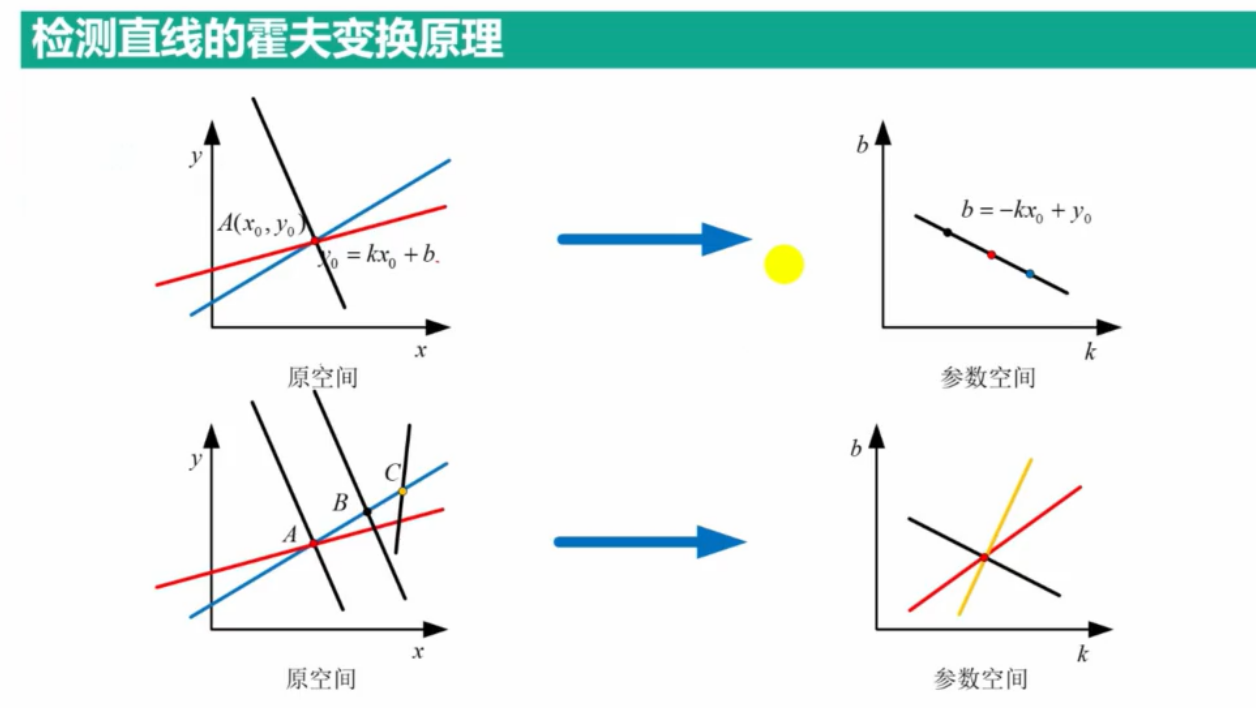
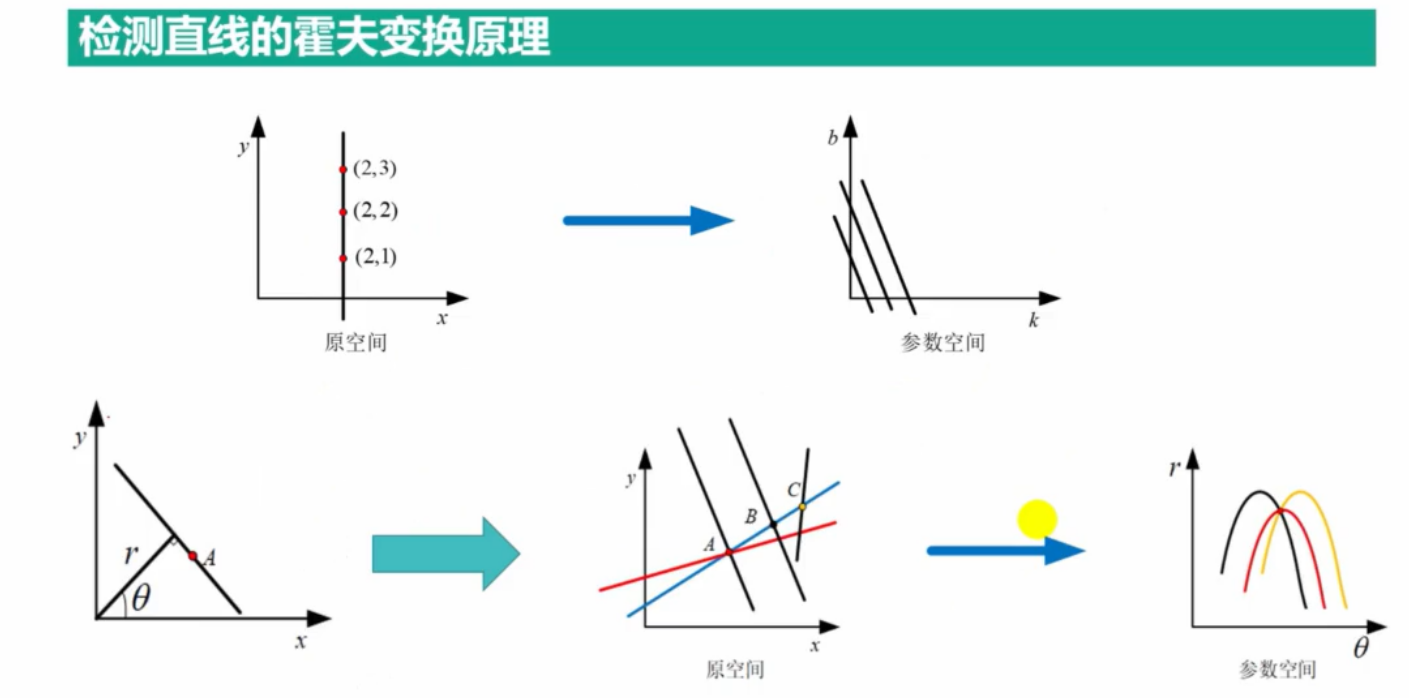
2.检测直线函数HoughLines()
检测直线流程:
Step1:将参数空间的坐标轴离散化。
Step2:将图像中每个非0像素通过映射关系求取在参数空间通过的方格
Step3:统计参数空间内每个方格出现的次数,选取次数大于某一值的方格作为表示直线的方格
Step4:将参数空间中表示直线的方格的参数作为图像中直线的参数
void cv::HoughLines ( InputArray image
OutputArray lines,
double rho,
double theta,
int threshold.
double srn = 0,
double stn =0,
double min_theta = 0,
double max_theta = CV_PI
)
参数说明:
- image:输入的二值图像,通常是经过边缘检测后的图像。
- lines:输出参数,包含检测到的直线的向量。
- rho:极径参数ρ的精确度,以像素为单位。
- theta:角度参数θ的精确度,以弧度为单位。
- threshold:参数空间中投票阈值,用于确定检测到的直线。
- srn、stn、min_theta、max_theta:这些参数是可选的,用于进一步细化直线检测的精度和范围。
示例代码:
void drawLine(Mat &img,//要标记直线的图像vector<Vec2f> lines,//检测的直线数据double rows,//原图像的行数(高)double cols,//原图像的列数(宽)Scalar scalar,//绘制直线的颜色int n//绘制直线的线宽){Point pt1,pt2;for(size_t i=0;i<lines.size();i++){float rho=lines[i][0];//直线距离坐标原点的距离float theta=lines[i][1];//直线过坐标原点垂线double a=cos(theta);//夹角的余弦值double b=sin(theta);//夹角的正弦值double x0=a*rho,y0=b*rho;//直线与坐标原点的垂线的交点double length=max(rows,cols);//图像高宽的最大值//计算直线上的一点pt1.x= cvRound(x0+length*(-b));pt1.y= cvRound(y0+length*(a));//计算直线上的另一点pt2.x= cvRound(x0-length*(-b));pt2.y= cvRound(y0-length*(a));//两点绘制一条直线line(img,pt1,pt2,scalar,n);}
}
//霍夫直线检测
void Hough_linear_detection(Mat image){Mat gray;cvtColor(image,gray,COLOR_BGR2GRAY);Mat edge;//检测边缘图像,并二值化Canny(gray,edge,80,180,3, false);//用不同的累加器进行检测直线vector<Vec2f> lines1,lines2;HoughLines(edge, lines1,1,CV_PI/180,50,0,0);HoughLines(edge, lines2,1,CV_PI/180,150,0,0);//在原图像中绘制直线Mat img1,img2;image.copyTo(img1);image.copyTo(img2);drawLine(img1,lines1,edge.rows,edge.cols,Scalar(255),2);drawLine(img2,lines2,edge.rows,edge.cols,Scalar(255),2);//显示图像imwrite("/sdcard/DCIM/edge.png",edge);imwrite("/sdcard/DCIM/img1.png",img1);imwrite("/sdcard/DCIM/img2.png",img2);
}
Canny算子边缘检测后图片 :

用累加器为50进行检测直线:

用累加器为150进行检测直线:

3.检测直线函数 HoughLinesP()
void cv::HoughLinesP ( InputArray image,
OutputArray lines,
double rho,
double theta,
int threshold,
double minLineLength =0,
double maxLineGap = 0
)
- image:待检测直线的原图像,必须是CV_8C的单通道二值图像
- lines:霍夫变换检测到的直线输出量,每一条直线都由4个参数进行描述,分别是直线两个端点的坐标
- rho:以像素为单位的距离分辨率。
- theta: 以弧度为单位的角度分辨率
- threshold:累加器的阈值
- minLineLength: 直线的最小长度,当检测直线的长度小于该数值时将会被剔除
- maxLineGap:允许将同一行两个点连接起来的最大距离。
示例代码:
//霍夫直线检测
void Hough_linearP_detection(Mat image){Mat gray;cvtColor(image,gray,COLOR_BGR2GRAY);Mat edge;//检测边缘图像,并二值化Canny(gray,edge,80,180,3, false);//利用渐进概率式霍夫变换提取直线vector<Vec4i> linesP1,linesP2;HoughLinesP(edge, linesP1,1,CV_PI/180,150,30,10);//两个点连接最大距离10HoughLinesP(edge, linesP2,1,CV_PI/180,150,30,30);//两个点连接最大距离30//绘制两个点连接最大距离10直线检测结果Mat img1;image.copyTo(img1);for(size_t i=0;i<linesP1.size();i++){line(img1,Point(linesP1[i][0],linesP1[i][1]),Point(linesP1[i][2],linesP1[i][3]),Scalar(255),3);}//绘制两个点连接最大距离30直线检测结果Mat img2;image.copyTo(img2);for(size_t i=0;i<linesP2.size();i++){line(img2,Point(linesP2[i][0],linesP2[i][1]),Point(linesP2[i][2],linesP2[i][3]),Scalar(255),3);}//显示图像imwrite("/sdcard/DCIM/img10.png",img1);imwrite("/sdcard/DCIM/img20.png",img2);
}
绘制两个点连接最大距离10直线检测结果:

绘制两个点连接最大距离30直线检测结果:
相关文章:

OpenCV(三十六):霍夫直线检测
1.检测直线的霍夫变换原理 2.检测直线函数HoughLines() 检测直线流程: Step1:将参数空间的坐标轴离散化。 Step2:将图像中每个非0像素通过映射关系求取在参数空间通过的方格 Step3:统计参数空间内每个方格出现的次数,选取次数大于某一值的方格作为表示直线的方格…...

文心一言 VS 讯飞星火 VS chatgpt (91)-- 算法导论8.3 4题
四、用go语言,说明如何在 O(n) 时间内,对 0 到 n 3 − 1 n^3-1 n3−1 区间内的n个整数进行排序。 文心一言: 在 O(n) 时间内对 0 到 n^3-1 区间内的 n 个整数进行排序,可以使用基数排序(Radix Sort)算法…...
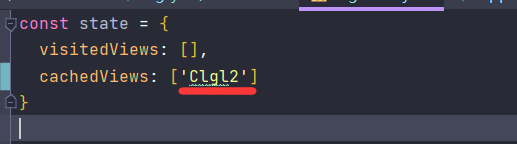
keep-alive缓存三级及三级以上路由
需求需要缓存这个出入记录,当tab切换时不重新加载,当刷新页面时,或把这个关闭在重新打开时重新加载如图: (我这里用的是芋道源码的前端框架) keep-alive 1、include 包含页面组件name的这些组件页面,会被…...
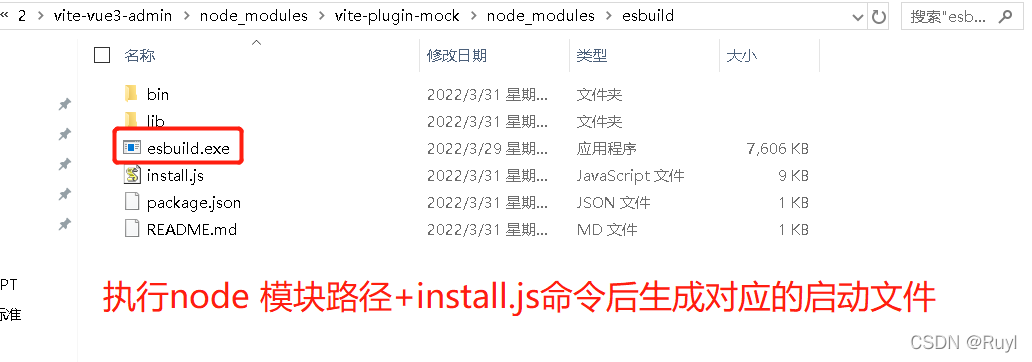
vite vue项目 运行时 \esbuild\esbuild.exe 缺失 错误码 errno: -4058, code: ‘ENOENT‘,
vite vue项目运行 npm run dev 报错某个模块启动文件丢失信息 D:\PengYe_code\2\vite-vue3-admin>npm run dev> vite-vue3-admin1.0.2 dev > vitenode:events:504throw er; // Unhandled error event^Error: spawn D:\PengYe_code\2\vite-vue3-admin\node_modules\vi…...
favicon.ico网站图标不显示问题 Failed to load resource: net::ERR_FILE_NOT_FOU
上述问题主要由于网站的小图标无法显示导致的:可以检查如下部分: 1、是否存在一个favicon.ico文件在根目录下 2、如果存在,看是否写的相对路径:改为绝对路径 <link rel"shortcut icon" href"../favicon.ico&quo…...
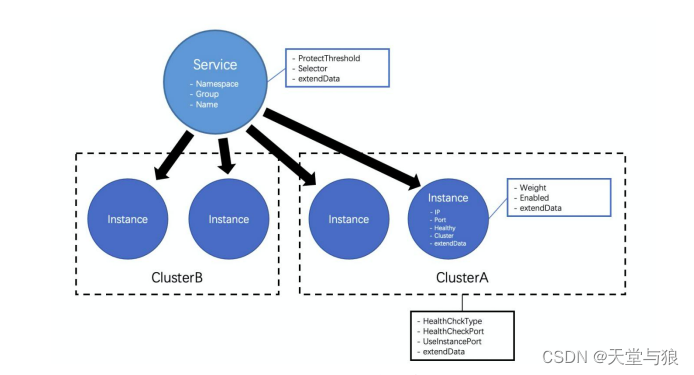
微服务·架构组件之服务注册与发现-Nacos
微服务组件架构之服务注册与发现之Nacos Nacos服务注册与发现流程 服务注册:Nacos 客户端会通过发送REST请求的方式向Nacos Server注册自己的服务,提供自身的元数据,比如ip地址、端口等信息。 Nacos Server接收到注册请求后,就会…...
Linux驱动【day2】
mychrdev.c: #include <linux/init.h> #include <linux/module.h> #include <linux/fs.h> #include<linux/uaccess.h> #include<linux/io.h> #include"head.h" unsigned int major; // 保存主设备号 char kbuf[128]{0}; unsigned int…...
4、Nginx 配置实例-反向代理
文章目录 4、nginx 配置实例-反向代理4.1 反向代理实例一4.1.1 实验代码 4.3 反向代理实例二4.3.1 实验代码 【尚硅谷】尚硅谷Nginx教程由浅入深 志不强者智不达;言不信者行不果。 4、nginx 配置实例-反向代理 4.1 反向代理实例一 实现效果:使用 nginx…...

2023年世界机器人大会回顾
1、前记: 本次记录是我自己去世界机器人博览会参观的一些感受,所有回顾为个人感兴趣部分的机器人产品分享。整个参观下来最大的感受就是科学技术、特别是机器人技术和人工智能毫无疑问地、广泛的应用在我们日常生活的方方面面,在安全巡检、特…...
Mac系统 AndroidStudio Missing essential plugin:org.jetbrains.android报错
打开Android Studio,提示 Missing essential plugin:org.jetbrains.android错误,产生的原因是Kotlin被禁用。 解决的方法是删除disabled_plugins.txt,Mac OS对应的路径为: /Users/xzh/Library/Application Support/Google/AndroidStudio202…...

读书笔记:多Transformer的双向编码器表示法(Bert)-1
多Transformer的双向编码器表示法 Bidirectional Encoder Representations from Transformers,即Bert; 本笔记主要是对谷歌Bert架构的入门学习: 介绍Transformer架构,理解编码器和解码器的工作原理;掌握Bert模型架构…...
第二证券:股利支付率和留存收益率的关系?
股利付出率和留存收益率是股票出资中非常重要的目标,它们可以反映公司的盈余才能和未来开展的潜力。那么,二者之间究竟有什么联系呢? 一、股利付出率和留存收益率的定义 股利付出率是指公司向股东分配的股息占当期净利润的比例,通…...

煤矿虚拟仿真 | 采煤工人VR虚拟现实培训系统
随着科技的发展,虚拟现实(VR)技术已经逐渐渗透到各个行业,其中包括煤矿行业。VR技术可以为煤矿工人提供一个安全、真实的环境,让他们在虚拟环境中进行实际操作和培训,从而提高他们的技能水平和安全意识。 由广州华锐互动开发的采煤…...
buuctf crypto 【[GXYCTF2019]CheckIn】解题记录
1.打开文件,发现密文 2.一眼base64,解密一下 3.解密后的字符串没有什么规律,看了看大佬的wp,是rot47加密,解密一下(ROT5、ROT13、ROT18、ROT47位移编码)...

微服务05-Docker基本操作
Docker的定义 1.什么是Docker Docker是一个快速交付应用、运行应用的技术: 可以将程序及其依赖、运行环境一起打包为一个镜像,可以迁移到任意Linux操作系统运行时利用沙箱机制形成隔离容器,各个应用互不干扰启动、移除都可以通过一行命令完…...

OpenHarmony创新赛|赋能直播第三期
开放原子开源大赛OpenHarmony创新赛赋能直播间持续邀请众多技术专家一起分享应用开发技术知识,本期推出OpenHarmony应用开发之音视频播放器和三方库的使用和方法,助力开发者掌握多媒体应用技术的开发能力和使用三方库提升应用开发的效率和质量࿰…...
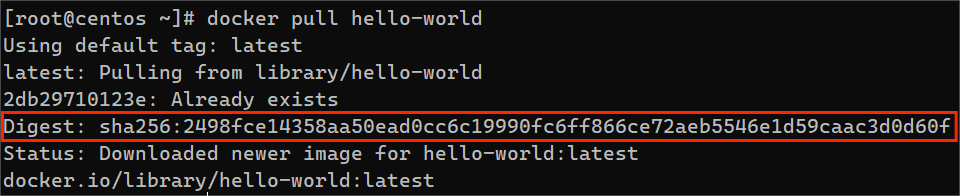
docker镜像详解
目录 什么是docker镜像镜像相关命令docker pulldocker imagesdocker searchdocker rmi导出 / 导入镜像 镜像分层镜像摘要镜像摘要的作用分发散列值 什么是docker镜像 Docker镜像是Docker容器的基础组件,它包含了运行一个应用程序所需的一切,包括代码、运…...
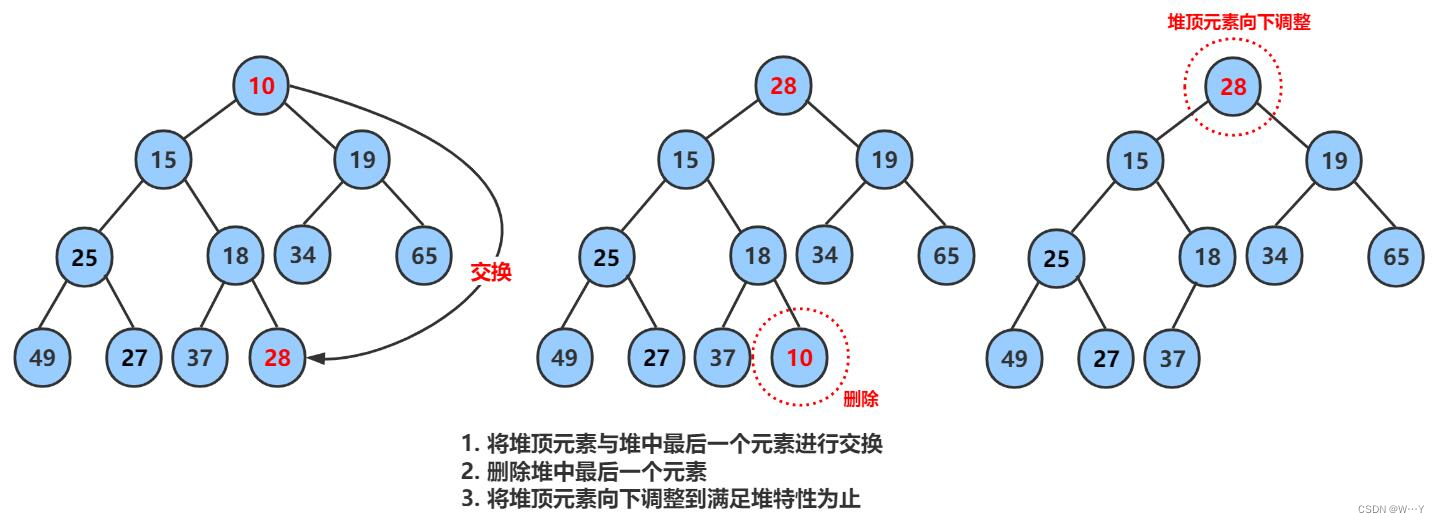
二叉树的顺序结构以及堆的实现——【数据结构】
W...Y的主页 😊 代码仓库分享 💕 上篇文章,我们认识了什么是树以及二叉树的基本内容、表示方法……接下来我们继续来深入二叉树,感受其中的魅力。 目录 二叉树的顺序结构 堆的概念及结构 堆的实现 堆的创建 堆的初始化与…...

手写一个摸鱼神器:使用python手写一个看小说的脚本,在ide中输出小说内容,同事直呼“还得是你”
文章目录 一、准备python环境二、分析小说网的章节目录三、分析小说网的章节内容四、编写python脚本五、验证一下吧 一、准备python环境 windows从0搭建python3开发环境与开发工具 Python爬虫基础(一):urllib库的使用详解 Python爬虫基础&a…...
【Python 实战】---- 实现批量图片的切割
1. 需求场景 在实际开发中,我们会遇到一种很无聊,但是又必须实现的需求,就是比如协议、大量的宣传页面、大量的静态介绍页面、或者大量静态页面,但是页面高度很高,甚至高度可能会达到50000px,但是为了渲染…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
