【基础算法】差分的应用(一维差分和二维差分)
🌹作者:云小逸
📝个人主页:云小逸的主页
📝Github:云小逸的Github
🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前,其次就是现在!学会自己和解,与过去和解,努力爱自己。==希望春天来之前,我们一起面朝大海,春暖花开!==🤟
👏专栏:C++👏 👏专栏:Java语言👏
👏专栏:C语言初阶👏👏专栏:数据结构👏
文章目录
- 前言
-
- 改变数组元素【一维差分】
- 题目:
- 输入格式
- 输出格式
- 数据范围
- 输入样例:
- 输出样例:
- 题目分析:
- 代码:
- 代码讲解:
- 1.memset函数
- 2.边界的代换
- 3.一维差分的模版:
- 差分矩阵【二维差分】
- 题目:
- 输入格式
- 输出格式
- 数据范围
- 输入样例:
- 输出样例:
- 题目分析:
- 核心思想:【二维差分】
- 代码:
-
- 最后
-
-
前言
今天这篇文章是接着上一篇文章【差分】展开说差分在题目中的妙用。如有错误,请私信告知,望见谅!
——————————————————————————————
首先先写上几句话:献给坚持创作的我和点开这篇文章希望进步的你
| 1.人一旦堕落,上帝就会以更快的速度收走你的天赋和力量。 |
| 2.这些年我一直提醒自己一件事情,千万不要自己感动自己。大部分人看似的努力,不过是愚蠢导致的。什么熬夜看书到天亮,连续几天只睡几小时,多久没放假了,如果这些东西也值得夸耀,那么富士康流水线上任何一个人都比你努力多了。 人难免天生有自怜的情绪,唯有时刻保持清醒,才能看清真正的价值在哪里。 ———于宙《我们这一代人的困惑》 |
| 3.改变自己,不要用力过猛,最好从小事开始。 比如说:点个赞,打败你的拖延症。 |
| 4、我始终认为一个人可以很天真简单的活下去,必是身边无数人用大的代价守护而来的。 ——《小王子》 |
| 5、如果你真的想做一件事情,那么就算障碍重重,你也会想尽一切办法去办到它。但若是你不是真心的想要去完成一件事情,那么纵使前方道路平坦,你也会想尽一切理由阻止自己向前。 |
改变数组元素【一维差分】
题目:
给定一个空数组 V 和一个整数数组 a1,a2,…,an。现在要对数组 V 进行 n 次操作。
第 i 次操作的具体流程如下:
从数组 V 尾部插入整数 0。
将位于数组 V 末尾的 ai 个元素都变为 1(已经是 1 的不予理会)。
注意:
ai 可能为 0,即不做任何改变。
ai 可能大于目前数组 V 所包含的元素个数,此时视为将数组内所有元素变为 1。
请你输出所有操作完成后的数组 V。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。每组数据第一行包含整数 n。
第二行包含 n 个整数 a1,a2,…,an。
输出格式
每组数据输出一行结果,表示所有操作完成后的数组 V,数组内元素之间用空格隔开。
数据范围
1≤T≤20000,
1≤n≤2×105,
0≤ai≤n,
保证一个测试点内所有 n 的和不超过 2×105。
输入样例:
3
6
0 3 0 0 1 3
10
0 0 0 1 0 5 0 0 0 2
3
0 0 0
输出样例:
1 1 0 1 1 1
0 1 1 1 1 1 0 0 1 1
0 0 0
题目分析:
可能你读完题,一下子没有理解是什么意思,没事,接下来这张动图便于你的理解:

希望看完这个动图你能理解这个题目

其实我们可以从题目这句话入手进行解题:
在这个数组内看这个数是0还是1:可以看这个数被操作的次数,如果操作0次,则是0,操作不是0次,则是1.
代码:
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;
const int N=200010;int n;
int b[N];int main()
{int T;scanf("%d",&T);while(T--){scanf("%d",&n);memset(b,0,(n+1)*4);for(int i=1;i<=n;i++){int a;scanf("%d",&a);int l=max(1,i-a+1),r=i;b[l]++;b[r+1]--;}for(int i=1;i<=n;i++){b[i]+=b[i-1];cout<<!!b[i]<<" ";}puts(" ");}return 0;
}
代码讲解:
1.memset函数


上面是memset函数的官方解释。
这里使用memset要注意,因为这里的测试数据比较大,如果直接初始化,代码可能过不了,因此要么使用for循环要么使用memset只初始化前n+1的数据也是可以的。
2.边界的代换

3.一维差分的模版:

差分矩阵【二维差分】
题目:
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n ,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例:
2 3 4 1
4 3 4 1
2 2 2 2
题目分析:
这道题目的意思是:给定原矩阵a[][],构造差分矩阵b[][],使得a[][]是b[][]的二维前缀和。
即a[i][j]是b[1][1]到b[i][j]的矩阵,就是下图的意思。

核心思想:【二维差分】
以(x1,x2)为左上角,(x2,y2)为右上角的子矩阵中的所有数a[i][j],加上C(常数)
如:
b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
代码:
#include <iostream>using namespace std;const int N = 1010;int n, m, q;
int a[N][N], b[N][N];void insert(int x1, int y1, int x2, int y2, int c)
{b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}int main()
{scanf("%d%d%d", &n, &m, &q);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )scanf("%d", &a[i][j]);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )insert(i, j, i, j, a[i][j]);while (q -- ){int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);}for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];for (int i = 1; i <= n; i ++ ){for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);puts("");}return 0;
}

最后
十分感谢你可以耐着性子把它读完和我可以坚持写到这里,送几句话,对你,也对我:
| 1.任何寻求安慰的行为都不会让你成长:宿醉、旅行、痛哭流涕、甚至和朋友的促膝长谈,都只是让你感觉安全、良好; 成长其实是特别艰难的自省,你必须抛弃所有说给别人和自己听的漂亮话,正视你的无能与不可得,甚至一遍一遍被怨恨愤怒及嫉妒撂倒,然后你才懂得:成长无关改变,只是学会选择你能承受的。 |
| 2.以前我觉得成绩不重要。清华 、北大、复旦、交大 ,只能代表学生时代的成就。后来我发现,努力是种习惯,它会贯穿终生。 |
| 3.除了自身的病患或亲友离去的痛苦是真实的,其他的痛苦都是你自己的价值观带给你的。 |
| 4、当你觉得自己想要死去时,你真的不是真想死,你只是不想这样活着。 |
| 5、你无所依靠,事必靠己。很多很多的钱以及很多很多的爱,你都可以自己给自己。自己给自己的安全感才最踏实,你的努力永远不会背叛你。 |
最后如果觉得我写的还不错,请不要忘记点赞✌,收藏✌,加关注✌哦(。・ω・。)
愿我们一起加油,奔向更美好的未来,愿我们从懵懵懂懂的一枚菜鸟逐渐成为大佬。加油,为自己点赞!
相关文章:

【基础算法】差分的应用(一维差分和二维差分)
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

第49章 API统一集中管理
1 关于统一集中管理API的一些思考 1、统一集中管理是保证工程性项目得保质、保量、成功实施,并对后期维护提供数据支撑的最有效,最节省资源和时间的技能和做法,软件做为一种特殊的工程性项目,也符合上述特性。 2、由于在前台实现中…...

carla0.9.13-UE4添加4轮车模型(Linux系统)
前期准备建模工具:blender:v3.4.1;可以在Ubuntu Software商店直接下载虚拟引擎:carla-UE4 (carla v0.9.13),无需额外安装UE4,carla中自带插件编译carla参照官方文档:https://carla.readthedocs.io/en/0.9.1…...
对比yolov4和yolov3
目录 1. 网络结构的不同 1.1 Backbone 1.1.1 Darknet53 1.1.2 CSPDarknet53 1.2 Neck 1.2.1 FPN 1.2.2 PAN 1.2.3 SPP 1.3 Head 2. 数据增强 2.1 CutMix 2.2 Mosaic 3. 激活函数 4. 损失函数 5. 正则化方法 知识点 记录备忘。 总体而言&…...

Android ServiceManager
1.ServiceManager ServiceManager在init进程启动后启动,用来管理系统中的Service。 一般开机过程分为三个阶段: ①OS级别,由bootloader载入linux内核后,内核开始初始化,并载入built-in的驱动程序,内核完成开机后,载入init process,切换至user-space后,结束内核的循…...
数据挖掘,计算机网络、操作系统刷题笔记53
数据挖掘,计算机网络、操作系统刷题笔记53 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,orac…...

地球板块运动vr交互模拟体验教学提高学生的学习兴趣
海陆变迁是地球演化史上非常重要的一个过程,它不仅影响着地球的气候、地貌、生物多样性等方面,还对人类文明的演化产生了深远的影响。为了帮助学生更加深入地了解海陆变迁的过程和机制,很多高校教育机构开始采用虚拟现实技术进行教学探究。 V…...

【Android玩机】跟大家聊聊面具Magisk的使用(安装、隐藏)
目录:1、Magisk中文网2、隐藏面具和Root(一共3种方法)1、Magisk中文网 (1)首先Magisk有一个中文网,对新手非常友好 (2)这网站里面主要包含:6 部分 (3)按照他给…...

DACS: Domain Adaptation via Cross-domain Mixed Sampling 学习笔记
DACS介绍方法Naive MixingDACSClassMix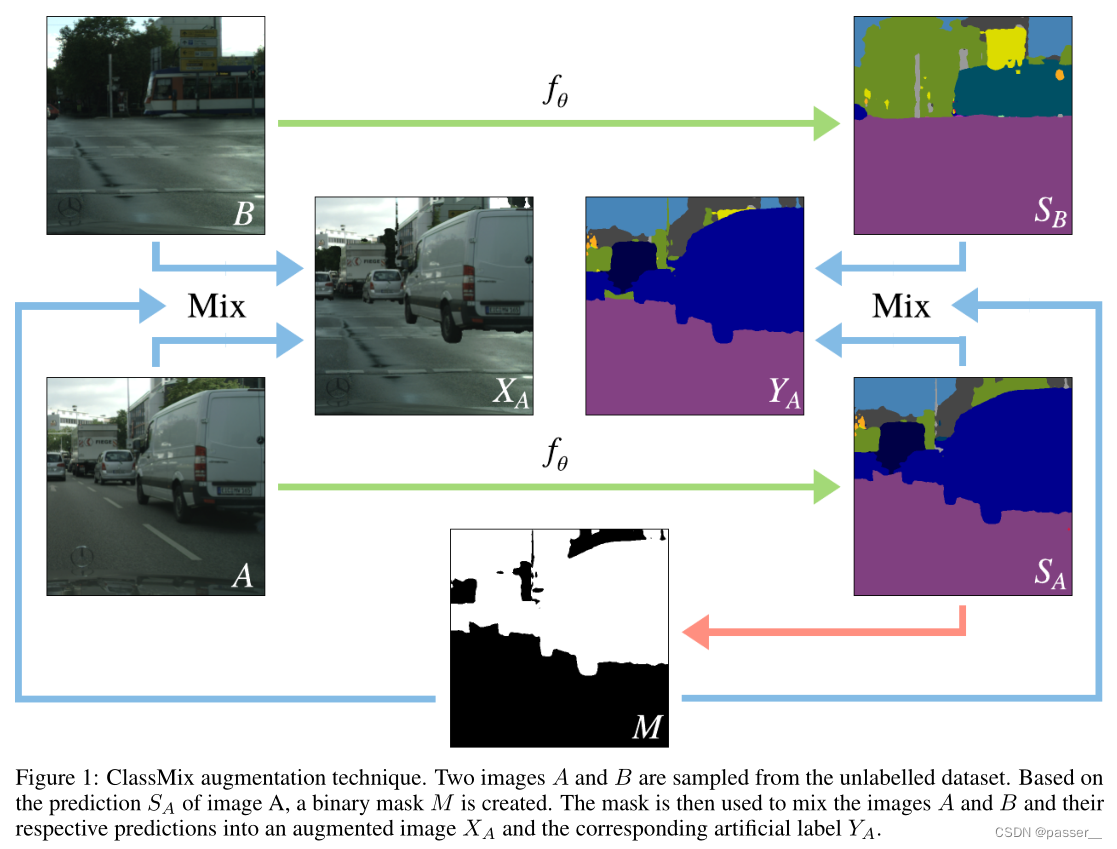算法流程实验结果反思介绍 近年来,基于卷积神经网络的语义分割模型在众多应用中表现出了显著的性能。然而当应用于新的领域时&…...

python并发编程(并发与并行,同步和异步,阻塞与非阻塞)
最近在学python的网络编程,学了socket通信,并利用socket实现了一个具有用户验证功能,可以上传下载文件、可以实现命令行功能,创建和删除文件夹,可以实现的断点续传等功能的FTP服务器。但在这当中,发现一些概…...
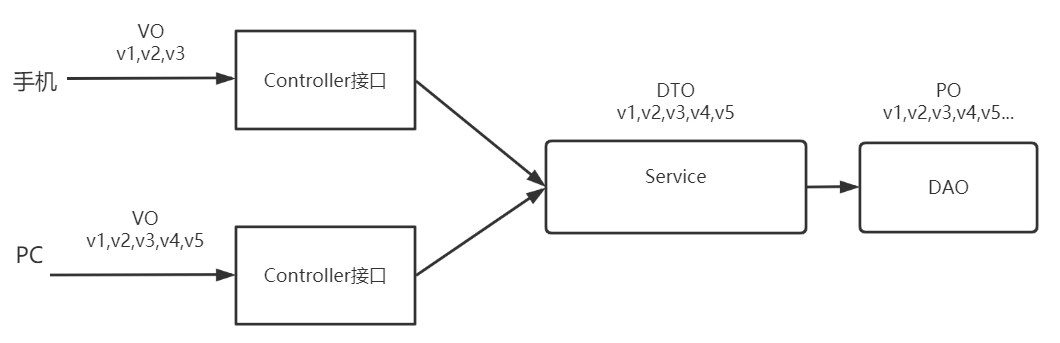
【项目】DTO、VO以及PO之间的关系和区别
【项目】DTO、VO以及PO之间的关系和区别 文章目录【项目】DTO、VO以及PO之间的关系和区别1.概念2. 作用1.概念 DTO:DTO是 Data Transfer Object 的缩写,也叫数据传输对象。 PO:PO是 Persistent Object 的缩写,也叫持久化对象。 …...

Nginx介绍
什么是Nginx? Nginx 是一款高性能的 http 服务器/反向代理服务器及电子邮件(IMAP/POP3)代理服务器。由俄罗斯的程序设计师伊戈尔西索夫(Igor Sysoev)所开发,官方测试 nginx 能够支支撑 5 万并发链接&#x…...

你什么档次?敢和我用一样的即时通讯平台WorkPlus?
现今,很多企业越来越青睐私有化部署,尤其是在选择组织内部即时通讯平台的时候,更是会提出私有化部署的需求。究其原因,企业选择私有化部署即时通讯软件完全是出于安全方面考虑。因此,越来越多的企业将眼光望向了本地化…...

学习资源 - 深度学习
文章目录PyTorchNLP语音CV深度学习其它在我过往博客笔记中,每个专项技术,前面我会贴上官网、官方文档、书籍教程等。 但有些topic,资源比较分散;一个博主/up主,也有可能有多个topic的分享,这里分享我遇到的…...
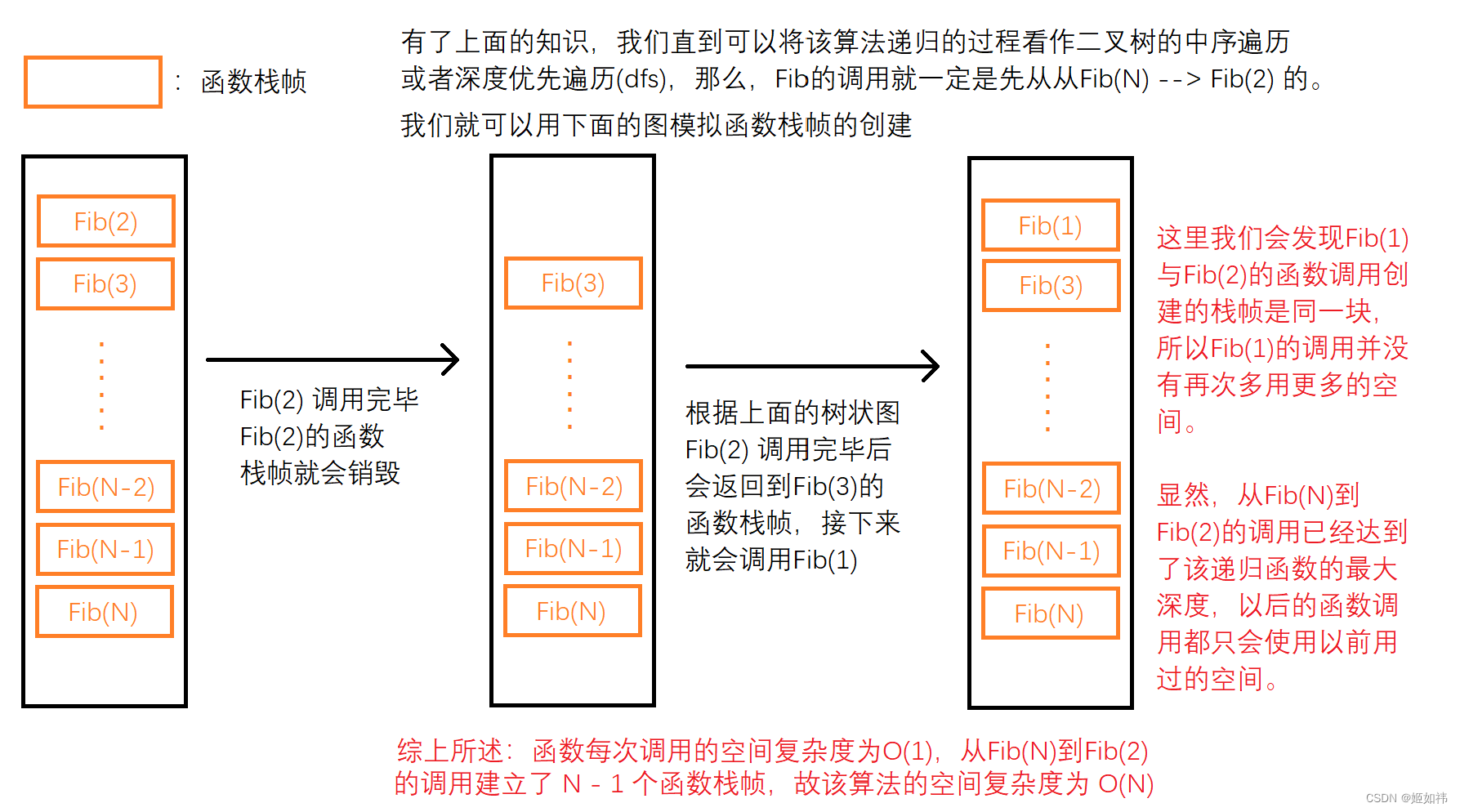
C语言数据结构初阶(1)----时空复杂度
目录 1. 数据结构,算法的概念 2. 算法的效率 2.1 算法复杂度 3. 时间复杂度 3.1 时间复杂度的概念 3.2 大O的渐进表示法 3.3 小试牛刀 4. 算法的空间复杂度 4.1 小试牛刀 1. 数据结构,算法的概念 数据结构(Data Structure)是计算机存储、组织数据…...
vscode SSH 保存密码自动登录服务器
先在win local上拿到秘钥,然后再把这秘钥copy 进服务器 1. 创建 RSA 密钥对 第一步是在客户端机器(通常是您的计算机 win 10)上创建密钥对:打开powershell, 输入 ssh-keygen默认情况下ssh-keygen将创建一个 2048 位 RSA 密钥对…...

VR全景多种玩法打破传统宣传,打造全新云端视界
传统的展示方式只是在进行单方面的表达,不论是图片、视频,都无法让浏览者有参与感,这样的展示宣传效果自然比不上VR全景展示,VR全景基于真实场景来形成三维图像,其沉浸式和无视野盲区的特点让用户更有真实感和沉浸感&a…...

Git 教程
目录1.简介:2.安装Git3.Git 如何工作状态区域4.使用Git5.Git配置5.1 创建仓库 - repository5.2 配置5.2.1 --global5.2.2 检查配置6. 查看工作区的文件状态6.1什么是工作区6.2 如果显示乱码的解决方式7.在工作区添加单个文件8. 添加工作区文件到暂存区9. 创建版本10…...

一种全新的图像滤波理论的实验(二)
一、前言 2021年12月31日,我发布了基于加权概率模型的图像滤波算法的第一个实验,当时有两个关键问题没有解决: 1、出现了大面积的黑色区域,最近考虑把这个算法实际应用在图像和视频的压缩领域,于是通过对程序的分析&a…...
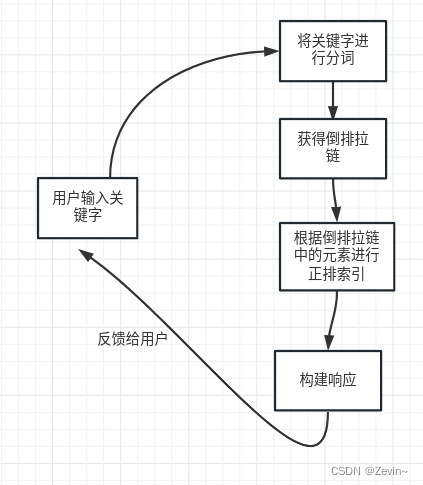
Boost库文档搜索引擎
文章目录综述效果展示去标签化,清理数据构建索引用户查询综述 该项目使用了BS架构,实现了用户对Boost库进行站内搜索的功能, 用户输入关键字使用http协议通过ajax将数据发送给后端服务器,后端进行分词, 通过倒排索引…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...
