基于大规模MIMO通信系统的半盲信道估计算法matlab性能仿真
目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
5.算法完整程序工程
1.算法运行效果图预览
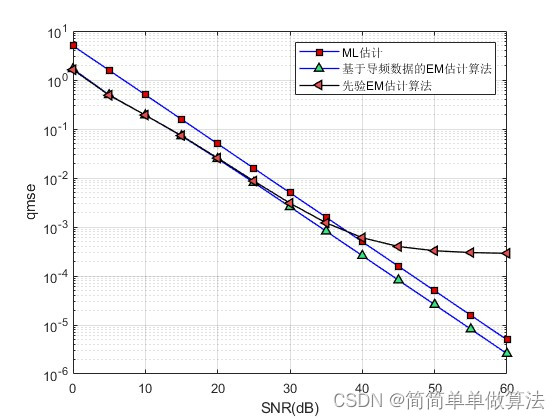
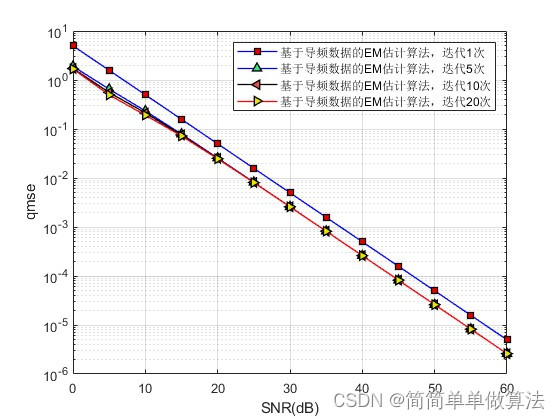
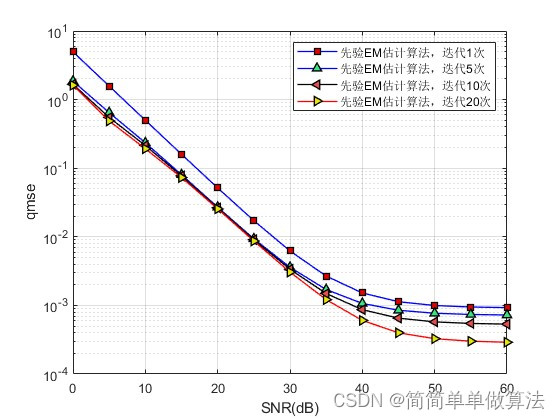
2.算法运行软件版本
matlab2022a
3.部分核心程序
%EM算法收敛所需的迭代
nIter = 1;
Yp = Y(:,1:L_polit,:); %与导频序列相对应的部分
qmse1 = zeros(1,len); %EM算法的MSE
for k=1:len %计算所有SNR的EM算法的MSEG0 = zeros(Nant,Nuser); %初始状态mIu0 = zeros(Nuser,N); sgm0 = zeros(Nuser,Nuser); for i=1:nIterG0 = (Yp(:,:,k)*Polits' + Y(:,L_polit:N-1,k)*mIu0(:,L_polit:N-1)')/ (Polits*Polits' + mIu0(:,L_polit:N-1)*mIu0(:,L_polit:N-1)' + (N-L_polit)*sgm0);for j=1:NmIu0(:,j) = (G0'*G0 + sigmaNu(k)*eye(Nuser))\(G0'*Y(:,j,k));endsgm0 = sigmaNu(k)*eye(Nuser)/(G0'*G0 + sigmaNu(k)*eye(Nuser));endqmse1(k) = trace(abs((G-G0)'*(G-G0)))/mean(beta2);
endnIter = 5;
Yp = Y(:,1:L_polit,:); %与导频序列相对应的部分
qmse2 = zeros(1,len); %EM算法的MSE
for k=1:len %计算所有SNR的EM算法的MSEG0 = zeros(Nant,Nuser); %初始状态mIu0 = zeros(Nuser,N); sgm0 = zeros(Nuser,Nuser); for i=1:nIterG0 = (Yp(:,:,k)*Polits' + Y(:,L_polit:N-1,k)*mIu0(:,L_polit:N-1)')/ (Polits*Polits' + mIu0(:,L_polit:N-1)*mIu0(:,L_polit:N-1)' + (N-L_polit)*sgm0);for j=1:NmIu0(:,j) = (G0'*G0 + sigmaNu(k)*eye(Nuser))\(G0'*Y(:,j,k));endsgm0 = sigmaNu(k)*eye(Nuser)/(G0'*G0 + sigmaNu(k)*eye(Nuser));endqmse2(k) = trace(abs((G-G0)'*(G-G0)))/mean(beta2);
end
614.算法理论概述
基于大规模MIMO通信系统的半盲信道估计算法涉及多个步骤,其原理和数学公式概括如下:
首先,MIMO系统需要发送已知的训练序列,在接收端进行初始的信道估计。当发送有用的信息数据时,接收端会利用初始的信道估计结果进行判决更新,以完成实时的信道估计。
在此基础上,半盲信道估计算法结合了盲估计和基于训练序列估计这两种方法的特点。一般来讲,通过设计训练序列或在数据中周期性地插入导频符号来进行估计是一种常见的方式。
半盲信道估计的数学公式可以表示为:
H^S = (1/T) * Σ_t=1^T [y_t * conj(H_t) / (1 + Σ_i=1^L * conj(H_i) * y_t * conj(H_i)^*)] (5)
其中,H^S是大规模MIMO信道的估计结果,y_t是接收信号向量,conj(H_t)是H_t的共轭转置,L是导频符号的数量,conj(H_i)^*是H_i的共轭转置的复数共轭。
这个公式基于盲估计的思想,利用了调制信号本身固有的、与具体承载信息比特无关的一些特征,或是采用了判决反馈的方法来进行信道估计。同时,通过在发送的有用数据中插入已知的导频符号,可以得到导频位置的信道估计结果,进而利用导频位置的信道估计结果,通过内插得到有用数据位置的信道估计结果。
因此,半盲信道估计算法不仅利用了基于训练序列的初始估计和实时判决更新,也结合了盲估计的方法特点,可以更加准确地估计大规模MIMO信道。
需要注意的是,半盲信道估计算法在实际应用中还需要考虑其他因素,如训练序列设计、导频符号的选择和插入、判决反馈机制的实现等。这些因素都可能对算法的性能和实际应用产生影响。因此,在实际应用中需要根据具体情况进行算法优化和调整。
5.算法完整程序工程
OOOOO
OOO
O
相关文章:

基于大规模MIMO通信系统的半盲信道估计算法matlab性能仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 %EM算法收敛所需的迭代 nIter 1; Yp Y(:,1:L_polit,:); %与导频序列相对应的部分 q…...
———— OVV Recall Rate与 IV Recall Rate)
自然语言处理学习笔记(九)———— OVV Recall Rate与 IV Recall Rate
目录 1.OVV Recall Rate 2. IV Recall Rate 1.OVV Recall Rate OOV指的是“未登录词”(Out Of Vocabulary),或者俗称的“新词”,也即词典未收录的词汇。如何准确切分00V,乃至识别其语义,是整个NLP领域的核…...

区块链正在开启一场回归商业,融合商业的新发展
对于区块链来讲,它其实同样在延续着这样一种发展路径。 正如上文所说,区块链正在开启一场回归商业,融合商业的新发展。 而欲要实现这一点,区块链就是要从底层算法,底层数据传输,底层体系的打造着手…...

【软考】系统集成项目管理工程师(三)信息系统集成专业技术知识③
一、云计算 1、定义 通过互联网来提供大型计算能力和动态易扩展的虚拟化资源;云是网络、互联网的一种比喻说法。是一种大集中的服务模式。 2、特点 (1)超大规模(2)虚拟化(3)高可扩展性&…...

js中如何判断一个对象是否为空对象?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 使用 Object.keys()⭐ 使用 for...in 循环⭐ 使用 JSON.stringify()⭐ 使用 ES6 的 Object.getOwnPropertyNames()⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带…...

Linux SysRq 简介
文章目录 1. 前言2. 背景3. Linux SysRq3.1 SysRq 简介3.1.1 SysRq 初始化 3.2 通过 procfs 发起 SysRq 请求3.2.1 修改内核日志等级3.2.1.1 触发3.2.1.2 实现简析 3.2.2 手动触发内核 panic3.2.2.1 触发3.2.2.2 实现简析3.2.2.3 应用场景 3.2.3 其它 SysRq 请求 3.3 通过 特殊…...
Mac版本破解Typora,解决Mac安装软件的“已损坏,无法打开。 您应该将它移到废纸篓”问题
一、修改配置文件 首先去官网选择mac版本下载安装 typora下载 然后打开typora包内容找到 /Applications/Typora.app/Contents/Resources/TypeMark/ 编辑器打开上面文件夹,这里我拉到vscode 找到page-dist/static/js/Licen..如下图 输入 hasActivated"…...
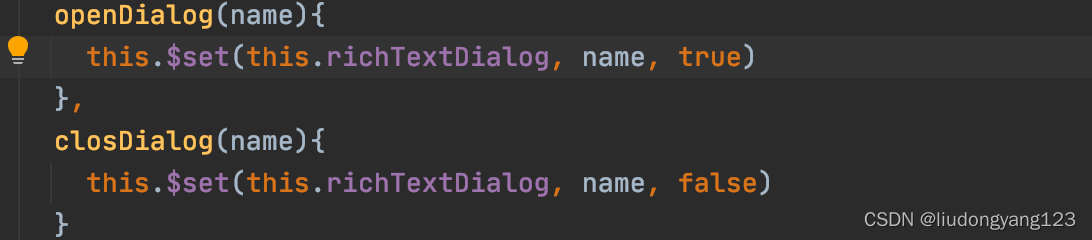
elementui el-dialog 动态生成多个,点击按钮打开对应的 dialog
业务场景: 根据后端返回的数据,动态生成表单,返回的数据中会有表单字段的类型,如果单选、多选、富文本,其它的属性还好说,重点说在富文本,因为我想通过 dialog 弹窗的方式,进行富文…...
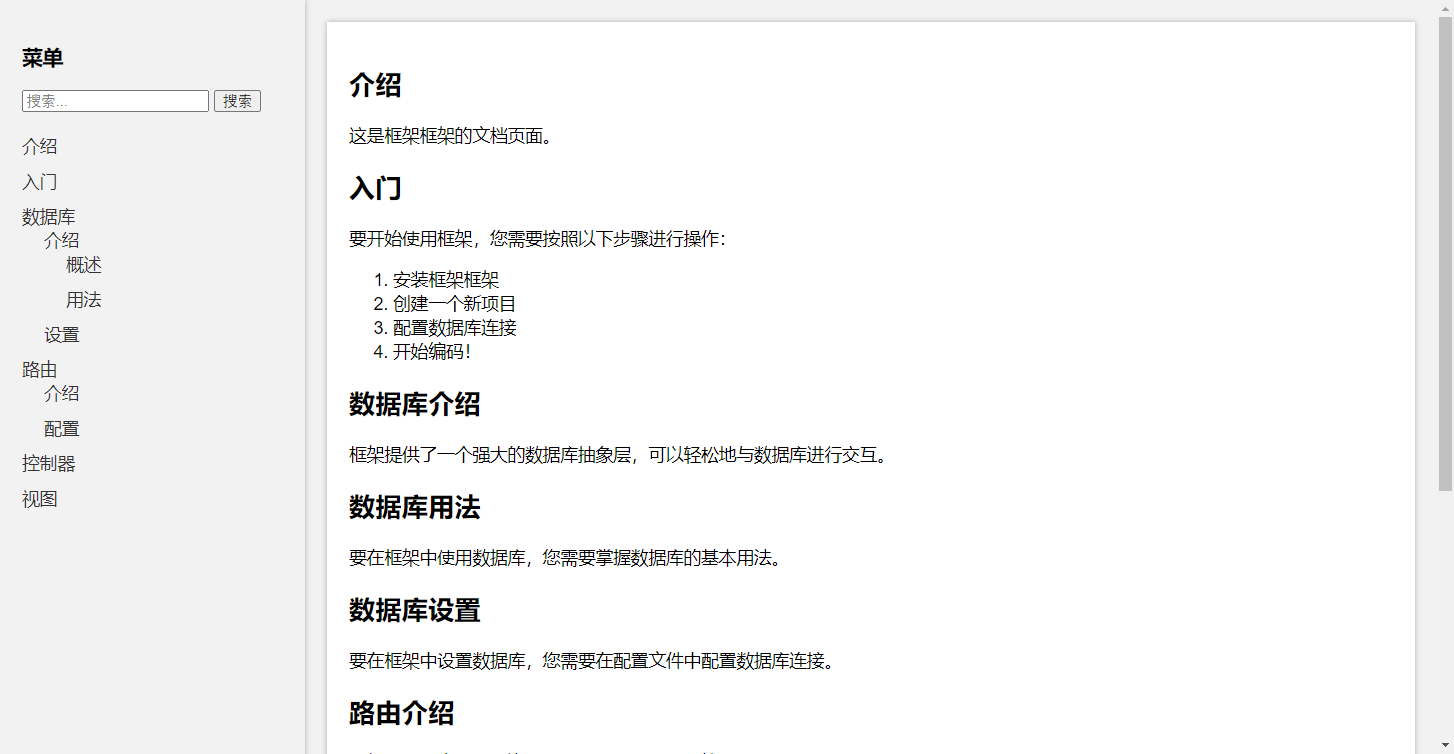
自己开发一个接口文档页面html
演示效果 具体代码如下 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>框架框架文档页面</…...

信息化发展28
区块链概述 区块链技术具有多中心化存储、隐私保护、防篡改等特点, 提供了开放、分散和容错的事务机制, 成为新一代匿名在线支付、汇款和数字资产交易的核心, 被广泛应用于各大交易平台, 为金融、监管机构、科技创新、农业以及政…...

React 入门实例教程
目录 一、HTML 模板 二、ReactDOM.render() 三、JSX 语法 四、组件 五、this.props.children 六、PropTypes 七、获取真实的DOM节点 八、this.state 九、表单 十、组件的生命周期 constructor() componentWillMount() render() componentDidMount() 组件生命周期…...
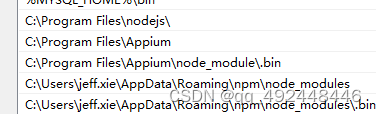
Window安装Node.js npm appium Appium Desktop
Window安装Node.js npm appium appium Desktop 1.安装nodejs 参考链接: https://blog.csdn.net/weixin_42064877/article/details/131610918 1)打开浏览器,并前往 Node.js 官网 https://nodejs.org/ ↗。 2)在首页中,您可以看到当前 Node.…...
 RNN分类)
Pytorch intermediate(三) RNN分类
使用RNN对MNIST手写数字进行分类。RNN和LSTM模型结构 pytorch中的LSTM的使用让人有点头晕,这里讲述的是LSTM的模型参数的意义。 1、加载数据集 import torch import torchvision import torch.nn as nn import torchvision.transforms as transforms import torc…...

vue2+webpack升级vue3+vite,修改插件兼容性bug
同学们可以私信我加入学习群! 前言 在前面使用electronvue3的过程中,已经验证了历史vue2代码vue3混合开发的模式。 本次旧项目vue框架整体升级中,同事已经完成了vue3、pinia、router等基础框架工具的升级。所以我此次记录的主要是vite打包工…...
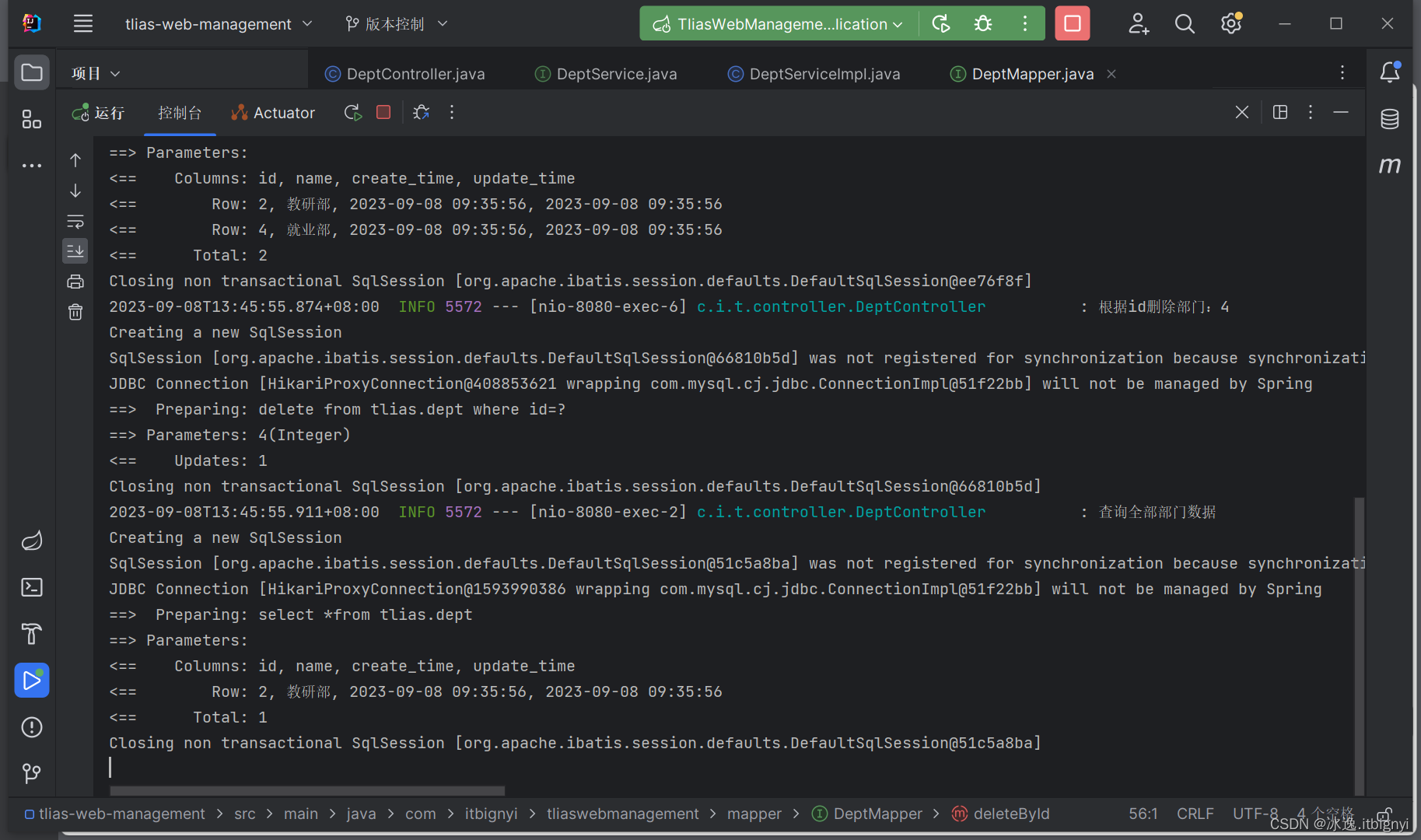
案例实战-Spring boot Web
准备工作 需求&环境搭建 需求: 部门管理: 查询部门列表 删除部门 新增部门 修改部门 员工管理 查询员工列表(分页、条件) 删除员工 新增员工 修改员工 环境搭建 准备数据库表(dept、emp) -- 部门管理…...

Spring6.1之RestClient分析
文章目录 1 RestClient1.1 介绍1.2 准备项目1.2.1 pom.xml1.2.2 创建全局 RestClient1.2.3 Get接收数据 retrieve1.2.4 结果转换 Bean1.2.5 Post发布数据1.2.6 Delete删除数据1.2.7 处理错误1.2.8 Exchange 方法 1 RestClient 1.1 介绍 Spring 框架一直提供了两种不同的客户端…...

冒泡排序、选择排序、插入排序、希尔排序
冒泡排序 基本思想 代码实现 # 冒泡排序 def bubble_sort(arr):length len(arr) - 1for i in range(length):flag Truefor j in range(length - i):if arr[j] > arr[j 1]:temp arr[j]arr[j] arr[j 1]arr[j 1] tempflag Falseprint(f第{i 1}趟的排序结果为&#…...

OpenCV(二十三):中值滤波
1.中值滤波的原理 中值滤波(Median Filter)是一种常用的非线性图像滤波方法,用于去除图像中的椒盐噪声等离群点。它的原理是基于邻域像素值的排序,并将中间值作为当前像素的新值。 2.中值滤波函数 medianBlur() void cv::medianBl…...

Prompt Tuning训练过程
目录 0. 入门 0.1. NLP发展的四个阶段: Prompt工程如此强大,我们还需要模型训练吗? - 知乎 Prompt learning系列之prompt engineering(二) 离散型prompt自动构建 Prompt learning系列之训练策略篇 - 知乎 ptuning v2 的 chatglm垂直领域训练记…...

装备制造企业是否要转型智能装备后服务型公司?
一、从制造到服务:装备制造企业的转型之路 装备制造企业作为国家经济发展的重要支柱,面临着日益激烈的市场竞争。在这样的背景下,越来越多的装备制造企业开始意识到,通过转型为智能装备后服务型公司,可以更好地满足客…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
