【LeetCode刷题笔记】动态规划 — 70.爬楼梯
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!!
主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步!
更多算法知识专栏:算法分析🔥
给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ

LeetCode题解专栏:【LeetCode刷题笔记】
目录
- 题目链接
- 一、题目描述
- 二、示例
- 三、题目分析
- dp数组的定义
- 基础情况
- 递推公式
- 四、代码实现(C++)
- 优化
题目链接
70. 爬楼梯- 力扣(LeetCode)
一、题目描述
假设你正在爬楼梯。需要n阶你才能到达楼顶。
每次你可以爬1或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
二、示例
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
三、题目分析
根据题目一次1个或2个台阶,先考虑极端情况:只有一个台阶的情况和只有两个台阶的情况
-
只有一个台阶:1种方法:爬1个台阶
-
只有两个台阶:2种方法:爬两次1个台阶、爬一次2个台阶
在两个台阶的问题中,第一种方法包含了只有一个台阶的情况(爬两次1个台阶:即爬了一个台阶,此时只剩下一个台阶,转化为了只有一个台阶的问题)
三个台阶时,如果爬1个台阶,还剩2个台阶,转化为了2个台阶的问题;如果爬两个台阶,还剩1个台阶,转化为了1个台阶的问题
因此,三个台阶的方法等于一个台阶的方法 + 两个台阶的方法,为动态规划问题
dp数组的定义
dp[i] 爬到第i层楼梯,有dp[i]种⽅法
基础情况
第1个台阶和第2个台阶为最基础的情况,分别是1种、2种方法
dp[1] = 1;
dp[2] = 2;
递推公式
由题目分析可得:dp[i] = dp[i-1] + dp[i-2]
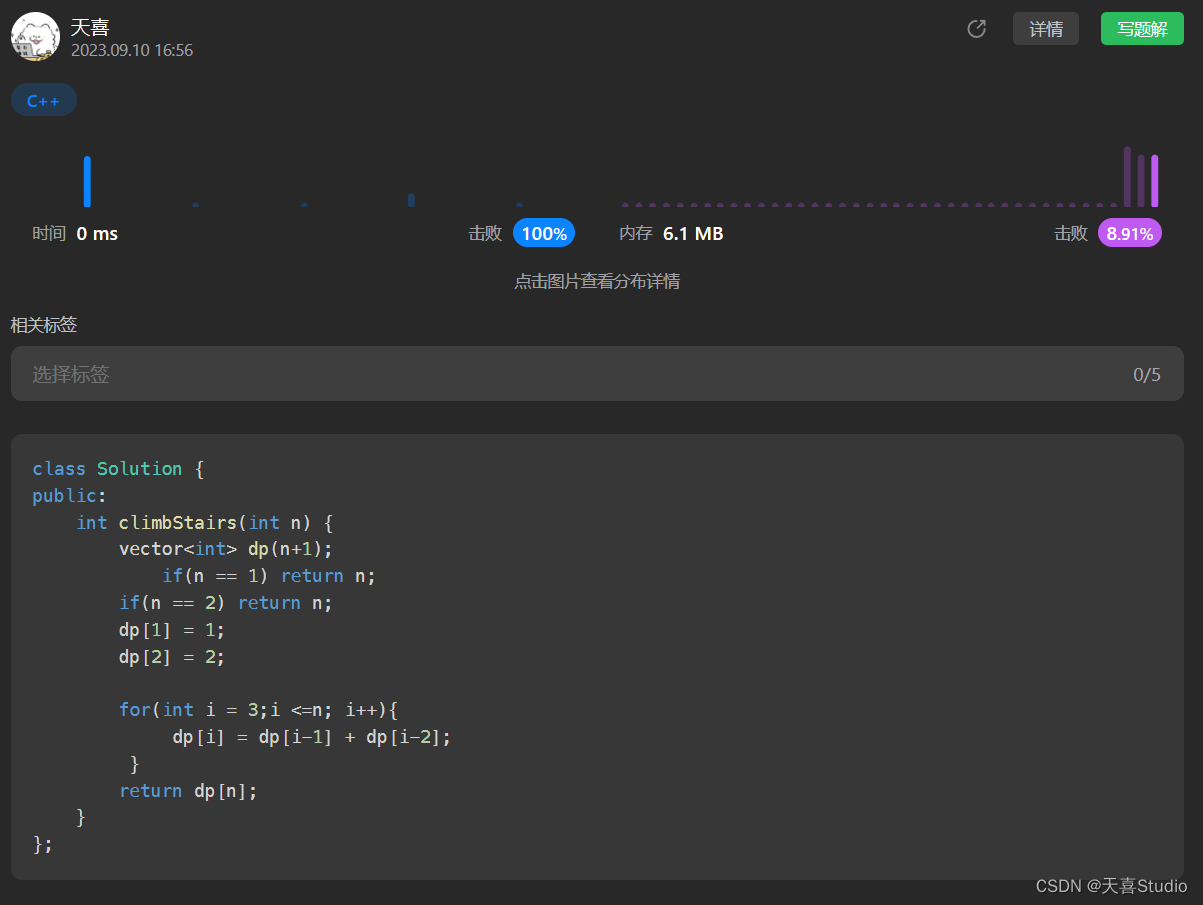
四、代码实现(C++)
class Solution {
public:int climbStairs(int n) {vector<int> dp(n+1);if(n == 1) return n;if(n == 2) return n;dp[1] = 1;dp[2] = 2;for(int i = 3;i <=n; i++){dp[i] = dp[i-1] + dp[i-2];}return dp[n];}
};
优化
以三个台阶为例,第三个台阶只依赖于前两个台阶的方法和,第i个台阶只依赖于i - 1 和i - 2的和
只需关注前两个的值,其余的可以不去考虑, vector<int> dp(n+1) 缩小为 dp[3],优化空间复杂度(在数据n较大的情况下)
class Solution {
public:int climbStairs(int n) {int dp[3]; //dp[0]占1个if(n == 1) return n;if(n == 2) return n;dp[1] = 1;dp[2] = 2;int sum = 0;for(int i = 3;i <=n; i++){sum = dp[1] + dp[2];dp[1] = dp[2];dp[2] = sum;}return dp[2];}
};
** **

| 大家的点赞、收藏、关注将是我更新的最大动力! 欢迎留言或私信建议或问题。 |
| 大家的支持和反馈对我来说意义重大,我会继续不断努力提供有价值的内容! |
| 如果本文哪里有错误的地方还请大家多多指出(●'◡'●) |
相关文章:

【LeetCode刷题笔记】动态规划 — 70.爬楼梯
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 更多算法知识专栏:算法分析🔥 给大家跳段街舞感谢…...
2024腾讯校招后端面试真题汇总及其解答(三)
21【算法题】反转链表 题目: 给定单链表的头节点 head ,请反转链表,并返回反转后的链表的头节点。 示例 1: 输入:head = [1,2,3,4,5] 输出:[5,4,3,2,1]示例 2: 输入:head = [1,2] 输出:[2,1]示例 3: 输入:head = [] 输出:[]提示: 链表中节点的数目范围是 [0, 5…...

mysql的分组group by
文章目录 一、介绍1、分组查询的内容2、多字段分组3、将查询内容连接group_concat4、有条件的分组查询having 一、介绍 将某个字段的相同值分为一组,分组查询的结果强调的是一个整体,每组内容只显示一行分组查询的内容一般要查询分组字段,因…...

Swoole 介绍以及 编译安装
Swoole是什么? Swoole是一个PHP语言的开源异步网络通信引擎,它是以PHP语言为基础,以C语言编写的扩展。它可以让PHP语言程序拥有异步网络通信能力,并且能够支持高并发、高性能的TCP/UDP/Unix Socket/HTTP服务器。 Swoole的优势 …...
Ubuntu终端指令
目录 目录 一、基本指令 1.命令行提示符 2.切换用户 3.修改密码 4.查看当前目录下的文件 5.修改文件权限---chmod 6.cd 切换路径 7.touch 8.cat 9.echo 10.mkdir 11. rm/rmdir 二、在线下载软件 1.更新软件源 2.更新软件列表 3.下载软件 三、离线安装软件 1. …...

python给json 转实体类加注释的代码实现
1 通过 GsonFormatPlus 生成的实体类 package com.zcl;import java.util.List;public class Test{/*** org_code*/private String org_code;/*** code*/private String code;/*** name*/private NameDTO name;/*** vendorextends*/private VendorextendsDTO vendorextends;/**…...
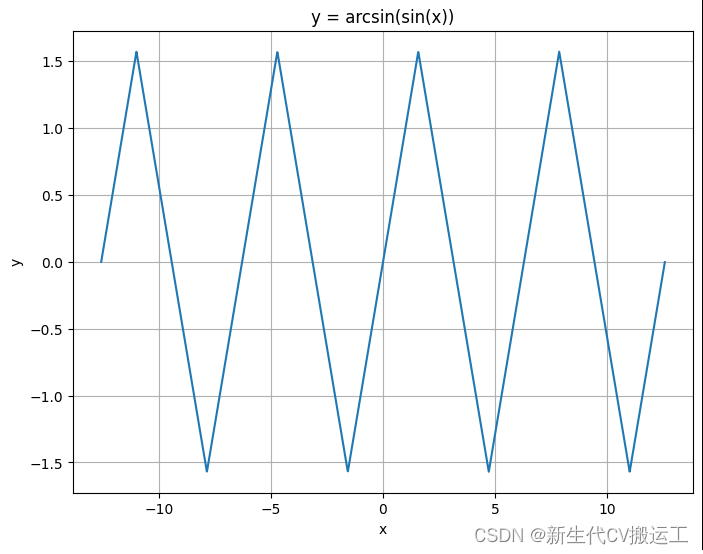
绘制三角波与梯形波
函数 使用三角函数及反三角函数 在线编辑运行工具 JupyterLite Retro - Notebook 三角波 import numpy as np import matplotlib.pyplot as plt # 创建一个从-2π到2π(包含2π)的等差数列,步长为0.01 x = np.arange(-4*np.pi, 4*np.pi, 0.01) # 计算y值 y = np.…...

【Git】 git push 提示Not possible to fast-forward,无法提交也无法提交程序
目录 一、执行rebase操作 二、取消rebase操作 错误内容 # git push To gitlab.aipark.com:aits/data-intergration.git! [rejected] zjk-prod-20230823 -> zjk-prod-20230823 (fetch first) error: failed to push some refs to gitlab.aipark.com:aits/data-in…...

优思学院|为什么质量工程师在别人看是“救火“的呢?
为什么质量工程师在别人看是‘救火’的呢?现今的质量管理体系已经很成熟,一家公司质量部门会有IQC、IPQC、OQC负责来料、过程质量、成品质量等等,而质量工程师(QE)的工作是要确保这些活动合理和有效,不产生…...

VMware Explore | 联想与VMware扩大合作带来生成式AI和多云解决方案
*带有 VMware Cloud 的全新联想 ThinkSystem 生成式 AI 解决方案,采用 NVIDIA 加速计算和软件,提供专为实现下一代 AI 工作负载而打造的 GPU 密集型平台。 联合创新实验室为商业中端市场和企业提供即用型混合多云解决方案。 全新 Lenovo TruScale Hybr…...
8月份徒弟企业面试后反馈的软件测试面试题(含金量高请收藏)
hello,我是清风。最近很多粉丝私信我要软件测试学习和面试资料,今天来安排一下面试题。我这里从来不缺永远不缺的就是面试提。我个人有几年软件测试面试官经验先不谈,我的徒弟每个月出去面试,我会叫他们录音。面试题都会反馈给我 …...

私有云不是真正的云计算!
大数据产业创新服务媒体 ——聚焦数据 改变商业 中国云计算遇到困境,IaaS层面,阿里云、腾讯云等增长乏力;SaaS没有发展起来。反观美国,整个云计算蓬勃发展,AWS、微软云、谷歌云体量更大,增速却不低&#x…...
netperf 测试时延和吞吐
一、Netperf是一种网络性能测试工具,主要基于TCP或UDP的传输。可以测量TCP和UDP传输的吞吐量、时延、CPU 占用率等性能参数。Netperf测试结果所反映的是一个系统能够以多块的速度向另一个系统发送数据,以及另一个系统能够以多块的速度接收数据。 二、打…...
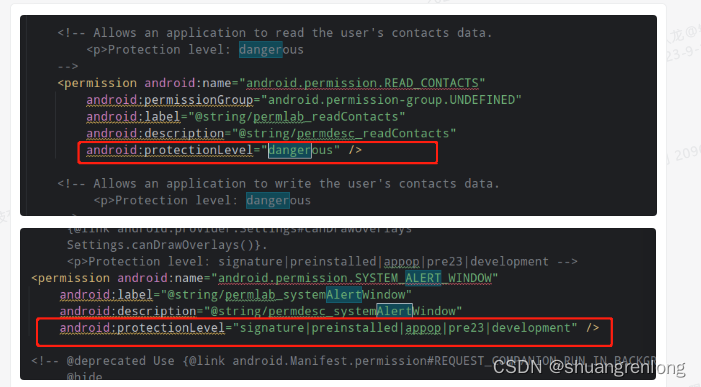
安卓预制权限添加规则
android:protectionLevel 可以在 android/frameworks/base/core/res/AndroidManifest.xml查询 signature|preinstalled 加在 这个文件里 privapp-permissions-xx.xml dangerous 加在 default-permissions/default-mega-permissions.xml normal 不需要加 不存在两个文件都加…...
D3JS简介
D3JS 什么是D3js D3.js是一个流行的JavaScript数据可视化库,它提供了一系列的API和工具,用于创建交互式的数据图表、地图等可视化效果。以下是一些D3.js的特点和用途: 数据驱动:D3.js基于数据驱动的思想,将数据和视觉…...
学习笔记----系统工程)
系统架构设计师(第二版)学习笔记----系统工程
【原文链接】系统架构设计师(第二版)学习笔记----系统工程 文章目录 一、系统工程方法1.1 系统工程方法的特点1.2 系统工程方法种类1.3 霍尔三维结构的7个阶段1.4 霍尔三维结构的7个步骤1.5 切克兰德方法的7个步骤1.6 并行工程的目标1.7 并行工程强调以下…...
java spring cloud 企业工程管理系统源码+二次开发+定制化服务
鸿鹄工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离构建工程项目管理系统 1. 项目背景 一、随着公司的快速发展,企业人员和经营规模不断壮大。为了提高工程管理效率、减轻劳动强度、提高信息处理速度和准确性,公司对内部工程管…...

IMX6ULL移植篇-boot 命令的学习
一. boot 命令简介 uboot 的作用是启动 Linux系统。所以 uboot 肯定有相关的 boot(引导)命令来启动 Linux。 常用的与 boot 有关的命令有:bootz、bootm 和 boot。 本文主要学习 boot 命令的使用。 本文接上一篇文章,如下: IMX6ULL移植篇…...

Python字典和集合操作指南:创建、获取值、修改和删除键值对,复制和遍历方法全解析
文章目录 字典(dict)创建字典获取字典中的值修改字典删除字典中的键值对复制字典字典推导式遍历字典使用keys()方法使用values()方法使用items()方法 小结 集合(set)创建集合集合操作集合运算小结 python精品专栏推荐python基础知…...

unity 接收拼接数据进行纹理替换且保存相机纹理到rtsp server(一)
1 rtsp 协议后编码解码 rtsp协议的问题就是,拼接完成后,还需要编码,而unity里面再需要解码,需要的过程多了一步编码再解码,大大加重了 2 rtsp 协议后轻量编码 rtsp协议使用mjpeg进行图片传输。why?这样做…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...

初级程序员入门指南
初级程序员入门指南 在数字化浪潮中,编程已然成为极具价值的技能。对于渴望踏入程序员行列的新手而言,明晰入门路径与必备知识是开启征程的关键。本文将为初级程序员提供全面的入门指引。 一、明确学习方向 (一)编程语言抉择 编…...

从数据报表到决策大脑:AI重构电商决策链条
在传统电商运营中,决策链条往往止步于“数据报表层”:BI工具整合历史数据,生成滞后一周甚至更久的销售分析,运营团队凭经验预判需求。当爆款突然断货、促销库存积压时,企业才惊觉标准化BI的决策时差正成为增长瓶颈。 一…...
