当前位置： 首页 > news >正文

【DevOps核心理念基础】3. 敏捷开发最佳实践

news 2026/2/9 19:13:50

一、敏捷开发最佳实践

1.1 项目管理

1.2 需求管理

1.3 技术架构

1.4 技术开发

1.5 测试

二、敏捷开发最佳实践

2.1 敏捷开发的执行细节

三、全面的DevOps工具链

四、版本控制和协作开发工具

4.1 集中式版本控制工具

4.2 分布式版本控制工具 

一、敏捷开发最佳实践

1.1 项目管理

  • 迭代开发

  • 技术团队的人员素质，人员配备完整

  • 及时有效的沟通方式，比如 每日会议、广告墙、任务板 等

  • 公开透明和项目技术和项目文档


1.2 需求管理

  • 需求订单 inbox，类似redmine，jira的订单显示方式

  • 业务流程简图

  • 用例驱动开发

  • 良好的处理通知机制

 

1.3 技术架构

  • 演进可行的基础资源、网络架构，每一步都是可用的

  • 演进可用的人机交互设计

  • 基于组件、插件、扩展的架构设计

 

1.4 技术开发

  • 结对编程（两个或多个员工沟通顺畅或者对某个业务属性分一个队完成任务）（只是建议）

  • 测试驱动开发（根据测试用例进行开发）（只是建议，需要看团队风格）

  • 代码重构（经常优化代码）

  • 代码安全和规范（后章节有专门工具）

 

1.5 ​​​​​​​测试

  • 单元编程

  • 并行测试（边开发边测试，模块或者类测试）

  • 完善的测试报告

 

二、敏捷开发最佳实践

2.1 敏捷开发的执行细节

  • 重要的目标是通过持续地及早交付有价值的软件使客户满意

  • 拥抱需求的变化，乐观面对需求，敏捷掌控软件生命周期

  • 经常地交付可工作的软件，倾向于采取较短的周期

  • 业务人员、开发人员、测试人员必须相互合作，高效沟通

  • 不论团队内外，传递信息效果最好效率也最高的方式是面对面的交谈

  • 可工作的软件是进度的首要度量标准

  • 不断地坚持针对软件开发，架构的优化，敏捷能力由此增强

  • 以简洁为本，它是极力减少不必要工作量的有效手段

  • 团队定期总结经验，反思自身，不断提高团队的专业水平

 

三、全面的DevOps工具链

  • 版本控制 & 协作开发 : GitHub、GitLab、SubVersion、 BitBucket

  • 自动化构建 和 测试: Maven 、Selenium、PyUnit、JUnit、PHPUnit

  • 持续集成&交付: Jenkins

  • 容器平台: Docker、Rocket、 Ubuntu ( LXC)、第三方厂商如(AWS/阿里云)

  • 配置管理: Saltstack、Ansible

  • 容器调度平台(常用于微服务): OpenShift、Cloud Foundry、Kubernetes.Mesosphere、 Docker Swarm

  • 日志管理: Logstash、CollectD、StatsD

  • 监控，警告&分析:Nagios、Ganglia、Sensu、zabbix、ICINGA、Graphite、 Kibana

四、版本控制和协作开发工具

4.1 集中式版本控制工具

  • 代表工具 SVN

  • 由一个中央服务器控制所有的文件版本，集中式管理

  • 所有客户端都可以对中央库进行操作，由中央服务器保证版本的统一

  • 特点是安全性不够好，针对中央服务器的通信比较频繁，如果版本库文件过多，服务器压力较

 

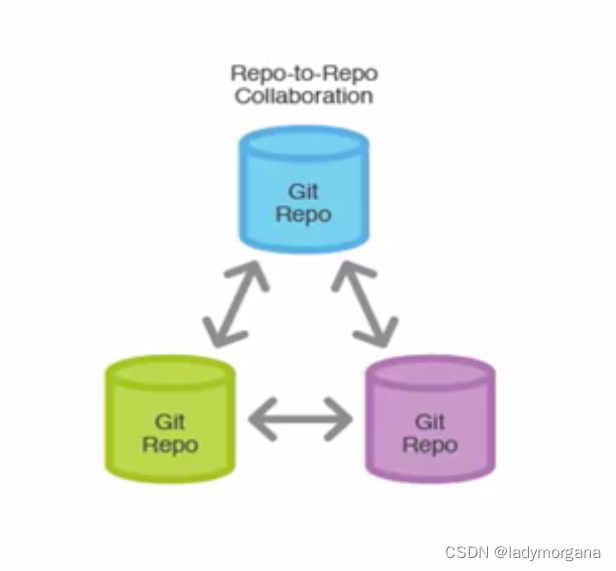
4.2 分布式版本控制工具 

  • 代表工具 GIT（推荐）

  • 本地就是一个中央服务器的完整镜像，直接提交到本地的镜像

  • 不依赖中央服务器的服务，不依赖网络，中央服务器负载压力小特点是 安全性好，每个开发者本地就是一个副本，储存也可以得到分布式架构的优化

 

相关文章：

【DevOps核心理念基础】3. 敏捷开发最佳实践

一、敏捷开发最佳实践 1.1 项目管理 1.2 需求管理 1.3 技术架构 1.4 技术开发 1.5 测试 二、敏捷开发最佳实践 2.1 敏捷开发的执行细节 三、全面的DevOps工具链 四、版本控制和协作开发工具 4.1 集中式版本控制工具 4.2 分布式版本控制工具 一、敏捷开发最佳实践 …...

编程日记 2023/9/12 21:40:03

二进制、数位dp：0912T3

考虑题目转化，二进制下满足 i ⊆ j , ( i x ) ⊆ ( j y ) i\subseteq j,(ix)\subseteq (jy) i⊆j,(ix)⊆(jy) 这显然是个数位dp形式 考虑枚举每一位与进位， d p k , p 1 , p 2 dp_{k,p_1,p_2} dpk,p1​,p2​​ 表示第 k − 1 k-1 k−1 位向第 k k…...

编程日记 2023/9/12 21:35:57

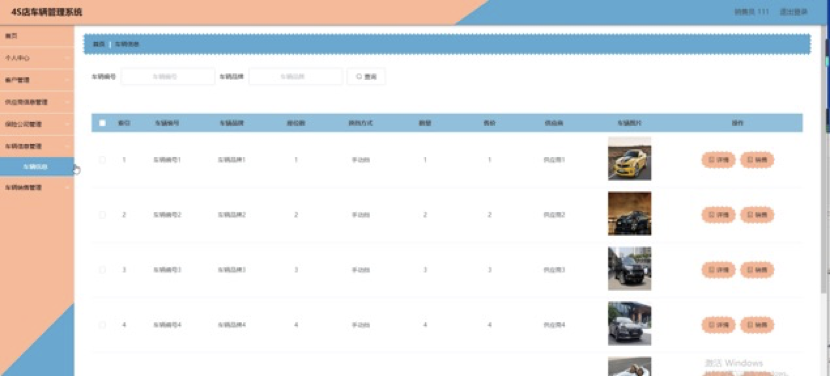
Java基于SpringBoot+Vue的 4S店车辆管理系统

博主介绍：✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 文章目录 1 简介2 技术栈3 功能总览4 系统设计4.1 系统设计主要功能4.2 数据库设计4.2.1 数据库设计规范4.2…...

编程日记 2023/9/12 21:33:55

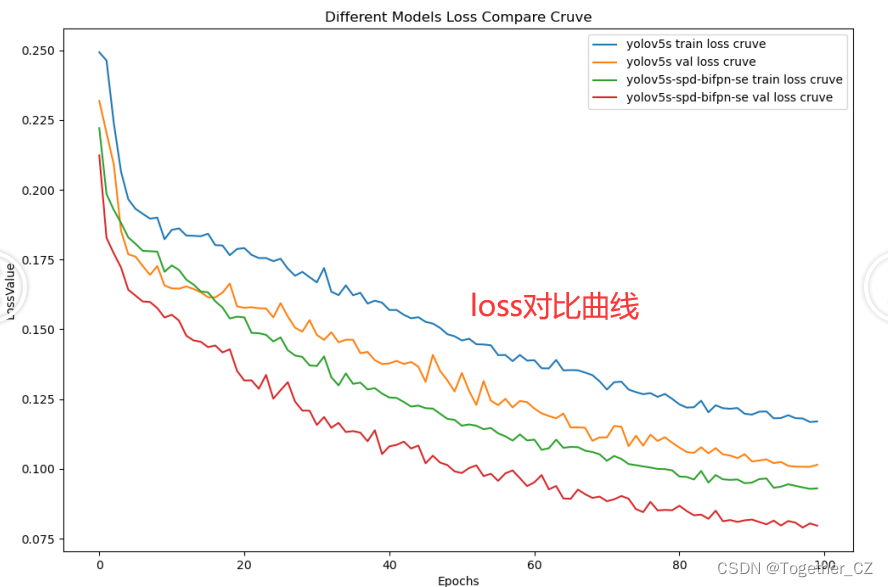
助力智能化公路养护，基于YOLOv5s集成SPD-BIFPN-SE开发构建公路开裂检测识别系统

在前文中我们尝试构建了在隧道、涵洞尝尽下的自动智能化养护巡查相关的模型，进行了实地测试评估，感兴趣的话可以自行移步阅读即可： 《基于轻量级YOLOv5s开发构建隧道基建裂痕、脱落等缺陷问题检测系统》 本文的想法是相近的，核心…...

编程日记 2023/9/12 21:31:53

C++--day5

实现一个图形类（Shape），包含受保护成员属性：周长、面积， 公共成员函数：特殊成员函数书写 定义一个圆形类（Circle），继承自图形类，包含私有属性：半…...

编程日记 2023/9/12 21:30:52

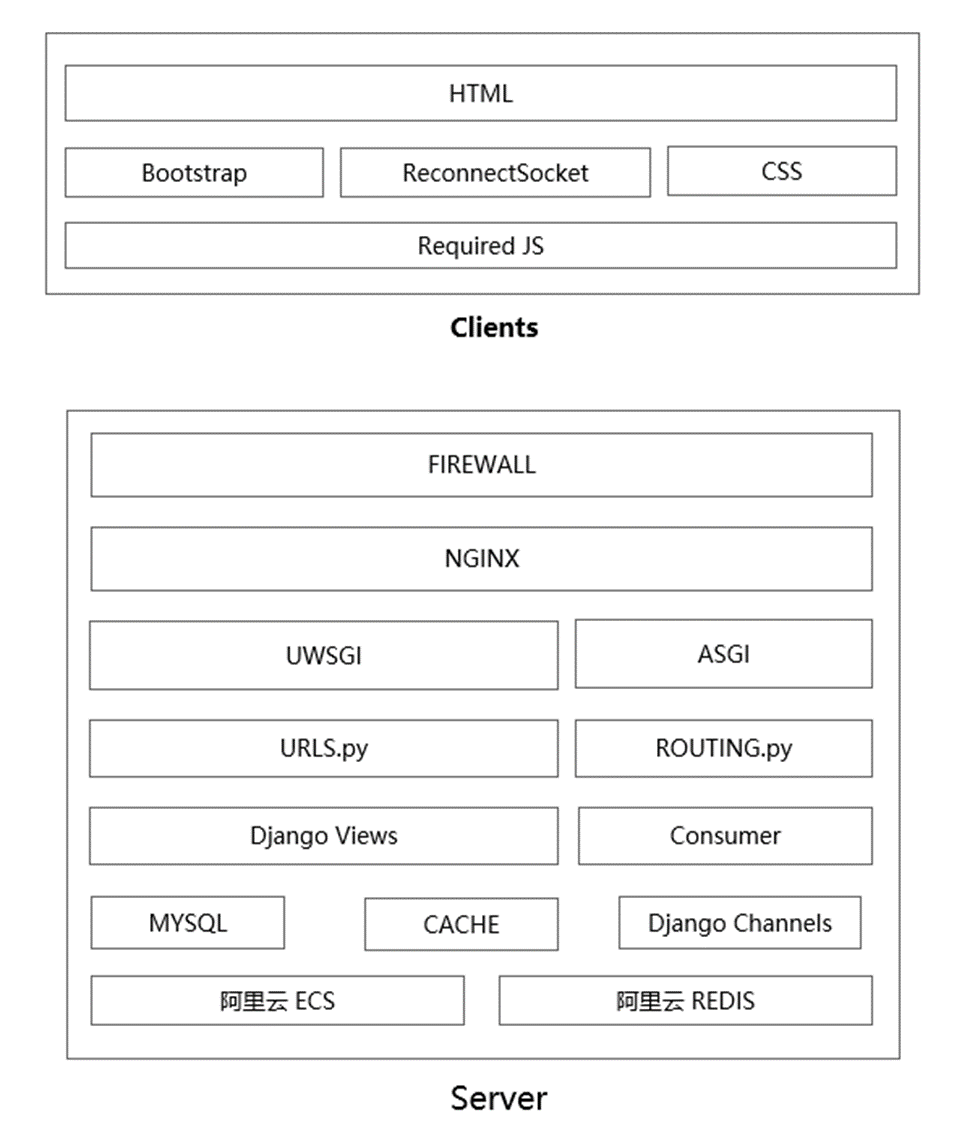
Django应用部署实战：从开发到生产，全程解析

部署架构图 版本说明 Centos 7.4 Python 3.6.4 Django 2.0.2 Channels 2.0.0 MySql 5.7 uWSGI Nginx 1.12.2 部署前 1、更新系统环境 yum install epel-release 2、安装所有的开发工具包 yum groupinstall -y “Development tools” 一、安装python 3.6.4 1、下载 cd /usr/…...

编程日记 2023/9/12 21:28:50

群晖NAS如何在内网部署HTTPS服务让浏览器信任证书

前言 最近在折腾内部部署Web服务。通过Vue实现一个H5的内部的管理服务。但在实际部署过程中由于种种原因，必须部署成Https服务。但在部署成Https服务后，由于没有HTTPS证书，每次进入页面都会被浏览器拦截。使用起来非常不便。于是开始各种Goo…...

编程日记 2023/9/12 21:26:47

crAPI靶场学习记录

靶场搭建 [靶场下载地址](我fork了一份) docker安装，笔者是用的wsldocker. [lab0:**初始账户 **] 注册一个账户，邮箱为[APIqq.com]，密码为Admin123 登陆后访问对应IP的8025端口，接收邮件获取车辆信息。 [lab1:**访问其它用户车…...

编程日记 2023/9/12 21:25:46

知识图谱实战应用28-基于py2neo的ICD-11疾病分类的知识图谱的查询与问答实战应用

大家好，我是微学AI，今天给大家介绍一下知识图谱实战应用28-基于py2neo的ICD-11疾病分类的知识图谱的查询与问答实战应用。使用基于py2neo的ICD-11疾病分类知识图谱，我们能够像探索一座生物医学宇宙般，穿梭在各种疾病之间。这个神奇的图谱可以帮助我们揭示各种疾病之间复杂而…...

编程日记 2023/9/12 21:23:45

20.Xaml GroupBox控件 ----＞带标题的内容控件

1.运行效果 2.运行源码 a.Xaml源码 <Window x:Class="testView.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d="http://schemas.mic…...

编程日记 2023/9/12 21:22:44

基于CycleGAN的山水风格画迁移

基于CycleGAN的山水风格画迁移 1、简介 1.1 研究背景及意义 绘画是人类重要的一种艺术形式&#xff0c;其中中国的山水画源远流长&#xff0c;具有丰富的美学内涵&#xff0c;沉淀着中国人的情思。游山玩水的大陆文化意识&#xff0c;以山为德、水为性的内在修为意识&#x…...

编程日记 2023/9/12 21:21:43

​@Cacheable 注解​

1. 功能说明 Cacheable 注解在方法上&#xff0c;表示该方法的返回结果是可以缓存的。也就是说&#xff0c;该方法的返回结果会放在缓存中&#xff0c;以便于以后使用相同的参数调用该方法时&#xff0c;会返回缓存中的值&#xff0c;而不会实际执行该方法。 注意&#xff0c;这…...

编程日记 2023/9/12 21:13:34

vue3+ts项目打包后的本地访问

注意&#xff1a;打包之后不可直接点击html访问&#xff0c;需要给项目安装本地服务&#xff01; 1、安装servenpm i -g serve 2、打包项目npm run build 生成dist文件夹 3、本地访问serve dist 运行service dist之后的控制台 可复制下方的地址运行打包后的项目&#xff0c;运行…...

编程日记 2023/9/12 21:10:30

探索程序员需要掌握的算法？

文章目录 一&#xff1a;引言二&#xff1a;常见算法介绍三&#xff1a;重点算法总结 &#x1f389;欢迎来到数据结构学习专栏~探索程序员需要掌握的算法&#xff1f; ☆* o(≧▽≦)o *☆嗨~我是IT陈寒&#x1f379;✨博客主页&#xff1a;IT陈寒的博客&#x1f388;该系列文章…...

编程日记 2023/9/12 21:09:29

性能测试 —— Jmeter定时器

固定定时器 如果你需要让每个线程在请求之前按相同的指定时间停顿&#xff0c;那么可以使用这个定时器&#xff1b;需要注意的是&#xff0c;固定定时器的延时不会计入单个sampler的响应时间&#xff0c;但会计入事务控制器的时间 1、使用固定定时器位置在http请求中&#xf…...

编程日记 2023/9/12 21:08:28

mp4视频太大怎么压缩？几种常见压缩方法

mp4视频太大怎么压缩&#xff1f;科技的飞速发展使得视频成为人们生活中不可或缺的一部分。然而&#xff0c;随着视频质量的不断提高&#xff0c;视频文件的大小也与日俱增&#xff0c;给我们的存储和传输带来了巨大的挑战和困扰。特别是MP4格式的视频&#xff0c;由于其出色的…...

编程日记 2023/9/12 21:07:27

论文复制ChatGPT按钮被发表，撤回后再曝多个类似案例；Midjourney 生成大师级的人像

&#x1f989; AI新闻 &#x1f680; 论文复制ChatGPT按钮被发表&#xff0c;撤回后再曝多个类似案例 摘要&#xff1a;一篇物理论文复制了ChatGPT按钮内容&#xff0c;经过两个月同行评审并在杂志上发表。这一现象被知名打假人发现后&#xff0c;发表商决定撤回该论文。此外…...

编程日记 2023/9/12 21:03:22

Python自动化测试 史上最全的进阶教程

Python自动化测试就是把以前人为测试转化为机器测试的一种过程。自动化测试是一种比手工测试更快获得故障反馈的方法。 随着时代的变革&#xff0c;也许在未来测试这个职位的需求会越来越少甚至消失&#xff0c;但是每一个组织&#xff0c;每一个客户对软件质量的要求是永远不…...

编程日记 2023/9/12 21:02:21

centos pip失效

在 CentOS 上安装和配置 pip3 可能需要以下步骤&#xff1a; 确保 Python 3 已正确安装&#xff1a;请确保您已经正确地安装了 Python 3。在 CentOS 上&#xff0c;Python 3 可能默认安装在 /usr/bin/python3 路径下。您可以通过运行以下命令来验证 Python 3 是否正确安装&…...

编程日记 2023/9/12 21:01:19

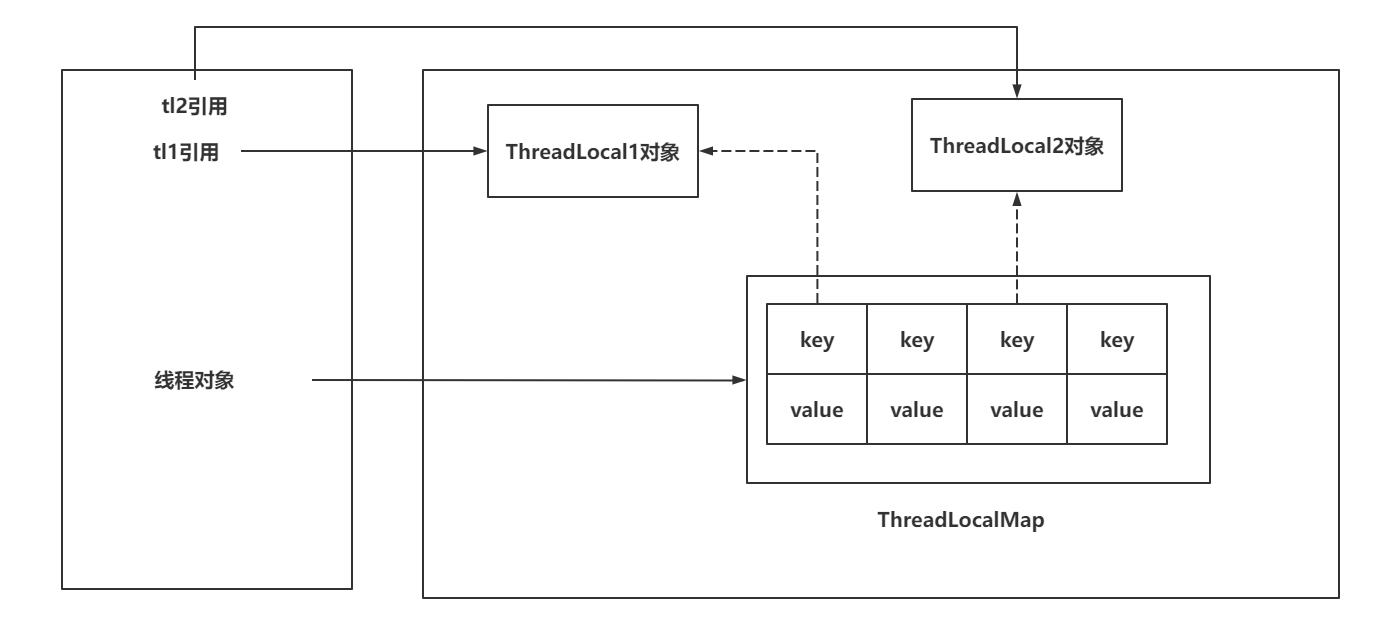
Java——》ThreadLocal

推荐链接&#xff1a; 总结——》【Java】 总结——》【Mysql】 总结——》【Redis】 总结——》【Kafka】 总结——》【Spring】 总结——》【SpringBoot】 总结——》【MyBatis、MyBatis-Plus】 总结——》【Linux】 总结——》【MongoD…...

编程日记 2023/9/12 20:59:17

iOS 26 携众系统重磅更新，但“苹果智能”仍与国行无缘

美国西海岸的夏天&#xff0c;再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至&#xff0c;这不仅是开发者的盛宴&#xff0c;更是全球数亿苹果用户翘首以盼的科技春晚。今年&#xff0c;苹果依旧为我们带来了全家桶式的系统更新&#xff0c;包括 iOS 26、iPadOS 26…...

编程新知 2026/2/8 20:41:56

应用升级/灾备测试时使用guarantee 闪回点迅速回退

1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间&#xff0c; 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点&#xff0c;不需要开启数据库闪回。…...

编程新知 2026/1/14 22:12:47

以下是对华为 HarmonyOS NETX 5属性动画（ArkTS）文档的结构化整理，通过层级标题、表格和代码块提升可读性：

一、属性动画概述NETX 作用&#xff1a;实现组件通用属性的渐变过渡效果&#xff0c;提升用户体验。支持属性&#xff1a;width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项&#xff1a; 布局类属性&#xff08;如宽高&#xff09;变化时&#…...

编程新知 2026/1/28 21:15:38

Redis数据倾斜问题解决

Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中&#xff0c;部分节点存储的数据量或访问量远高于其他节点&#xff0c;导致这些节点负载过高&#xff0c;影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

编程新知 2026/1/27 19:28:11

DeepSeek 技术赋能无人农场协同作业：用 AI 重构农田管理 “神经网”

目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

编程新知 2025/9/24 13:35:36

rnn判断string中第一次出现a的下标

# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

编程新知 2025/9/24 16:25:00

华硕a豆14 Air香氛版，美学与科技的馨香融合

在快节奏的现代生活中&#xff0c;我们渴望一个能激发创想、愉悦感官的工作与生活伙伴&#xff0c;它不仅是冰冷的科技工具&#xff0c;更能触动我们内心深处的细腻情感。正是在这样的期许下&#xff0c;华硕a豆14 Air香氛版翩然而至&#xff0c;它以一种前所未有的方式&#x…...

编程新知 2026/1/29 14:27:00

Go 语言并发编程基础：无缓冲与有缓冲通道

在上一章节中&#xff0c;我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道&#xff0c;它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好&#xff0…...

编程新知 2026/1/29 3:25:02

现有的 Redis 分布式锁库（如 Redisson）提供了哪些便利？

现有的 Redis 分布式锁库&#xff08;如 Redisson&#xff09;相比于开发者自己基于 Redis 命令&#xff08;如 SETNX, EXPIRE, DEL&#xff09;手动实现分布式锁&#xff0c;提供了巨大的便利性和健壮性。主要体现在以下几个方面&#xff1a; 原子性保证 (Atomicity)&#xff…...

编程新知 2025/9/23 11:26:04

【C++特殊工具与技术】优化内存分配(一)：C++中的内存分配

目录 一、C 内存的基本概念​ 1.1 内存的物理与逻辑结构​ 1.2 C 程序的内存区域划分​ 二、栈内存分配​ 2.1 栈内存的特点​ 2.2 栈内存分配示例​ 三、堆内存分配​ 3.1 new和delete操作符​ 4.2 内存泄漏与悬空指针问题​ 4.3 new和delete的重载​ 四、智能指针…...

编程新知 2026/1/31 6:12:22