【算法基础】时间复杂度和空间复杂度
目录
1 算法的评价
2 算法复杂度
2.1 时间复杂度(Time Complexity)
2.1.1 如何计算时间复杂度:
2.1.2 常见的时间复杂度类别与示例
2.2 空间复杂度
2.2.1 如何计算空间复杂度
2.2.2 常见的空间复杂度与示例
3 时间复杂度和空间复杂度计算示例
例子1:计算数组中所有元素的和。
例子2:快速排序算法。
例子3:递归实现斐波那契数列。
例子4:非递归实现的斐波那契数列。
例子5:二分查找算法。
例子6:冒泡排序算法。
1 算法的评价
评价算法的性能和效果是计算机科学和数据科学中的关键任务之一。如何评价算法的优劣可以从以下几方面展开:

时间复杂度和空间复杂度是算法性能分析的关键指标,它们用于衡量算法在处理不同规模输入时的时间和空间资源消耗。
2 算法复杂度
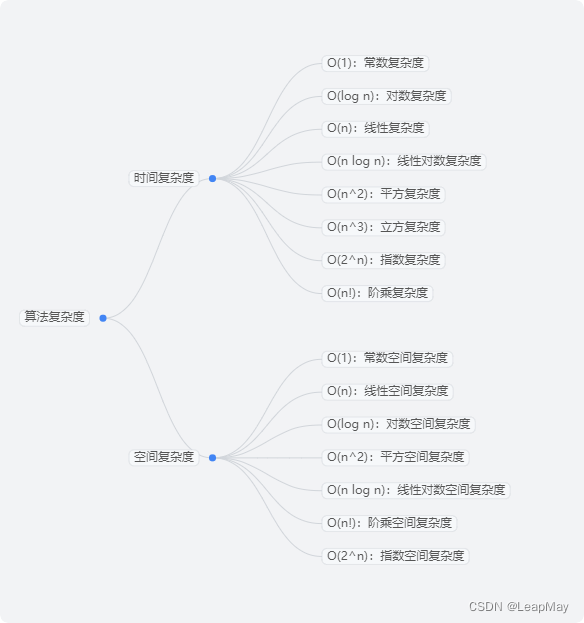
2.1 时间复杂度(Time Complexity)
时间复杂度是指在算法执行过程中,所需的时间资源与问题规模之间的关系。它主要衡量的是算法的执行效率,用于评估算法在不同规模数据下的操作时间。
时间复杂度通常使用大O符号表示,表示算法运行时间的增长率。
需要注意的是,时间复杂度只考虑算法的主要操作数量级,忽略了常数因子和低阶项。因此,两个时间复杂度相同的算法在实际执行中可能有着不同的执行效率。
2.1.1 如何计算时间复杂度:
- 分析每个操作的时间复杂度,包括循环、条件语句和函数调用。
- 计算每个操作的执行次数,通常是输入规模的函数。
- 合并所有操作的复杂度,通常选择最大的那个作为算法的时间复杂度。
时间复杂度的计算涉及以下几个方面:
基本操作次数: 时间复杂度的计算通常关注算法中执行的基本操作次数,例如赋值操作、比较操作、算术运算等。通常将这些操作的数量与输入规模相关联。
循环结构: 如果算法包含循环结构(例如for循环、while循环),需要考虑循环的迭代次数以及每次迭代中的基本操作数量。
递归调用: 对于递归算法,需要考虑递归的深度以及每次递归调用的时间复杂度。通常使用递归方程(递归关系式)来表示递归算法的时间复杂度。
分支结构: 如果算法包含分支结构(例如if语句),需要考虑每个分支的执行次数以及分支中的基本操作数量。
输入规模: 时间复杂度的计算通常与输入规模有关。输入规模表示算法操作的数据量或问题的大小,通常用符号n表示。
2.1.2 常见的时间复杂度类别与示例
常数时间复杂度(O(1)):无论问题规模多大,算法的执行时间都保持不变。例如,直接访问数组中的一个元素。
线性时间复杂度(O(n)):随着问题规模的增大,算法的执行时间也按线性比例增长。例如,遍历一个数组或链表中的所有元素。
对数时间复杂度(O(logn)):算法执行时间随着问题规模的增大而增长,但不是线性关系,而是以对数速率增长。例如,二分查找算法。
平方时间复杂度(O(n^2)):算法的执行时间与问题规模的平方成正比。例如,双重循环嵌套的算法。
指数时间复杂度(O(2^n)):算法的执行时间呈指数级增长,非常低效。例如,穷举法解决NP完全问题。
O(1) - 常数时间复杂度: 算法的执行时间是固定的,与输入规模无关。示例:
def constant_time_algorithm(arr):return arr[0]
O(log n) - 对数时间复杂度: 算法的执行时间随着输入规模的增加以对数方式增加。示例:
def binary_search(arr, target):low, high = 0, len(arr) - 1while low <= high:mid = (low + high) // 2if arr[mid] == target:return midelif arr[mid] < target:low = mid + 1else:high = mid - 1return -1
O(n) - 线性时间复杂度: 算法的执行时间与输入规模成正比。示例
def linear_search(arr, target):for i in range(len(arr)):if arr[i] == target:return ireturn -1
O(n^2) - 平方时间复杂度: 算法的执行时间与输入规模的平方成正比。示例:
def bubble_sort(arr):n = len(arr)for i in range(n):for j in range(0, n-i-1):if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]
2.2 空间复杂度(Space Complexity)
空间复杂度是指算法在执行过程中所需的额外内存空间,它与问题规模之间的关系。空间复杂度用于评估算法的内存占用情况和资源消耗。
通常使用大O符号表示空间复杂度,表示算法所需的额外内存空间与问题规模之间的增长关系。
2.2.1 如何计算空间复杂度
- 分析算法的每个数据结构、变量和递归调用,以确定它们的空间占用。
- 计算每个数据结构和变量的空间占用,通常是常数项和与输入规模相关的项的和。
- 合并所有空间占用,通常选择最大的那个作为算法的空间复杂度。
空间复杂度的计算包括以下几个方面:
固定内存消耗: 指算法在运行过程中需要固定数量的内存空间,与输入规模无关。常见的固定内存消耗包括函数参数、常量变量、全局变量等。
额外数据结构: 如果算法使用了额外的数据结构来存储信息,如数组、列表、树、堆栈、队列等,需要考虑这些数据结构所占用的内存空间。通常需要考虑数据结构的大小和数量。
递归调用: 递归算法会使用栈空间来存储每一次递归调用的状态。递归的深度和每次递归调用的内存消耗会影响空间复杂度。
临时变量: 算法中使用的临时变量和计算过程中的中间结果也会占用内存空间。需要考虑这些变量的数量和大小。
输入数据的存储: 输入数据的存储也需要考虑在内。如果算法需要将整个输入数据存储在内存中,则空间复杂度与输入数据的大小成正比。
2.2.2 常见的空间复杂度与示例
常数空间复杂度(O(1)):算法所需的额外内存空间是一个常量值,不随问题规模的增大而改变。例如,只使用固定数量的变量或常量大小的数组。
线性空间复杂度(O(n)):算法所需的额外内存空间随问题规模的增大而线性增长。例如,需要根据输入构建一个同等大小的新数据结构。
平方空间复杂度(O(n^2)):算法所需的额外内存空间随问题规模的增大而平方级增长。例如,需要构建一个二维数组来存储所有可能的组合。
指数空间复杂度(O(2^n)):算法所需的额外内存空间随问题规模的增大而以指数级增长。例如,需要存储所有可能的子集或排列。
需要注意的是,空间复杂度只考虑算法本身所需的额外内存空间,不包括输入数据所占用的存储空间。另外,空间复杂度也可以根据最坏情况或平均情况来进行分析。
O(1) - 常数空间复杂度: 算法的内存使用与输入规模无关,占用固定的内存空间。示例:
def constant_space_algorithm(arr):result = 0for num in arr:result += numreturn result
O(n) - 线性空间复杂度: 算法的内存使用与输入规模成正比。示例:
def linear_space_algorithm(n):arr = [0] * nreturn arr
O(n^2) - 平方空间复杂度: 算法的内存使用与输入规模的平方成正比。示例:
def quadratic_space_algorithm(n):arr = [[0] * n for _ in range(n)]return arr
3 时间复杂度和空间复杂度计算示例
例子1:计算数组中所有元素的和。
def sum_array(arr):sum = 0for num in arr:sum += numreturn sum时间复杂度:O(n),其中n是数组中的元素数量。遍历数组需要依次访问每个元素一次,因此时间复杂度与数组的大小成线性关系。
空间复杂度:O(1)。算法只使用了一个额外的变量存储累加和,并没有占用随问题规模变化的额外内存。
例子2:快速排序算法。
def quicksort(arr, left, right):if left < right:pivot = partition(arr, left, right)quicksort(arr, left, pivot - 1)quicksort(arr, pivot + 1, right)def partition(arr, left, right):pivot = arr[right]i = left - 1for j in range(left, right):if arr[j] <= pivot:i += 1arr[i], arr[j] = arr[j], arr[i]arr[i + 1], arr[right] = arr[right], arr[i + 1]return i + 1时间复杂度:最好情况下为O(nlogn),最坏情况下为O(n^2)。快速排序平均情况下的划分操作需要O(n)的时间复杂度,且需要递归n次,因此总体复杂度为O(nlogn)。但在最坏情况下,划分不平衡导致某一边的规模接近n,此时的时间复杂度变为O(n^2)。
空间复杂度:最好情况下为O(logn),最坏情况下为O(n)。快速排序使用递归调用,每次递归调用都需要保存当前函数的堆栈信息,而在最坏情况下,可能需要递归n次,所以空间复杂度为O(n)。而在最好情况下,递归调用树的高度为logn,因此空间复杂度为O(logn)。
例子3:递归实现斐波那契数列。
def fibonacci(n):if n <= 0:return 0if n == 1:return 1return fibonacci(n - 1) + fibonacci(n - 2)时间复杂度:指数级别,为O(2^n)。由于递归调用会重复计算相同的斐波那契数,时间复杂度呈指数级增长。
空间复杂度:最好和最坏情况下均为O(n),取决于递归调用的最大深度n。每次递归调用都需要在堆栈中保存函数的局部变量和参数,因此空间复杂度为O(n)。
该代码实现了递归方式计算斐波那契数列的函数。
时间复杂度:指数级别,为 O(2^n)。每次递归调用都会产生两个新的递归调用,因此递归树的总节点数是指数级别的,递归树的深度是 n。所以,总体的时间复杂度是 O(2^n)。
空间复杂度:指数级别,为 O(n)。在递归调用过程中,需要使用栈来保存每次递归调用的参数和局部变量。由于递归树的深度是 n,所以空间复杂度是 O(n)。
需要注意的是,由于斐波那契数列的计算可以通过动态规划或迭代的方式进行优化,以降低时间复杂度和空间复杂度。递归方式计算斐波那契数列在面对较大的 n 值时,会导致非常高的时间和空间消耗。
例子4:非递归实现的斐波那契数列。
def fibonacci(n):if n <= 0:return 0a = 0b = 1for _ in range(2, n+1):c = a + ba = bb = creturn b这段代码实现了求解斐波那契数列的函数。
该代码的时间复杂度是 O(n),其中 n 是要计算的斐波那契数的索引。在 for 循环中,需要执行 n-1 次加法操作。因此,时间复杂度是线性级别的。
该代码的空间复杂度是 O(1),因为除了输入参数外,只使用了常数空间来存储变量 a、b 和 c。无论输入的 n 多大,空间占用都是固定的。
例子5:二分查找算法。
def binary_search(arr, target):low = 0 # 常数时间复杂度high = len(arr) - 1 # 常数时间复杂度while low <= high:mid = (low + high) // 2 # 常数时间复杂度if arr[mid] == target:return midelif arr[mid] < target:low = mid + 1else:high = mid - 1return -1
该算法的时间复杂度为O(logn),在二分查找算法中,每次迭代会将问题规模缩小一半,因此时间复杂度为对数级别。具体而言,时间复杂度是由二分查找的迭代次数决定的。
空间复杂度是 O(1),因为除了输入参数外,没有使用额外的数据结构或变量来存储数据。无论输入规模如何变化,空间占用都是固定的。
例子6:冒泡排序算法。
def bubble_sort(arr):n = len(arr)for i in range(n): # 线性时间复杂度for j in range(0, n-i-1): # 线性时间复杂度if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]时间复杂度是 O(n^2),其中 n 是数组 arr 的长度。冒泡排序算法的时间复杂度由两层嵌套循环决定。外层循环执行 n 次,内层循环从 0 到 n-i-1 遍历,其中 i 是外层循环的迭代次数。因此,总的比较次数是 n + (n-1) + (n-2) + ... + 2 + 1,即等差数列求和公式,可以简化为 (n^2 - n) / 2,近似为 n^2。因此,该代码的时间复杂度是 O(n^2)。
该代码的空间复杂度是 O(1),因为除了输入参数外,没有使用额外的数据结构或变量来存储数据。无论输入规模如何变化,空间占用都是固定的。
计算时间复杂度和空间复杂度通常需要分析算法的每个操作以及它们的频率和内存占用。最终,选择合适的数据结构和算法以及考虑性能优化策略都有助于确保算法在不同规模的问题上都能高效运行。
相关文章:

【算法基础】时间复杂度和空间复杂度
目录 1 算法的评价 2 算法复杂度 2.1 时间复杂度(Time Complexity) 2.1.1 如何计算时间复杂度: 2.1.2 常见的时间复杂度类别与示例 2.2 空间复杂度 2.2.1 如何计算空间复杂度 2.2.2 常见的空间复杂度与示例 3 时间复杂度和空间复杂度…...

解决微信小程序不支持TextEncoder/TextDecoder对象
问题描述:在使用小程序开发者工具开发小程序中使用到了CRC算法,其中有一行代码使用到了TextEncoder对象,在开发工具中一切正常,到手机上会报出错误错误如下: MiniProgramError TextEncoder is not defined ReferenceEr…...

Qt下SVG格式图片应用
SVG格式图片介绍 svg格式图片又称矢量图,该种格式的图片不同于png等格式的图片,采用的并不是位图的形式来组织图片,而是采用线条等组织图片,svg格式是图片的文件格式是xml,可以通过文件编译器打开查看svg格式内容。 …...
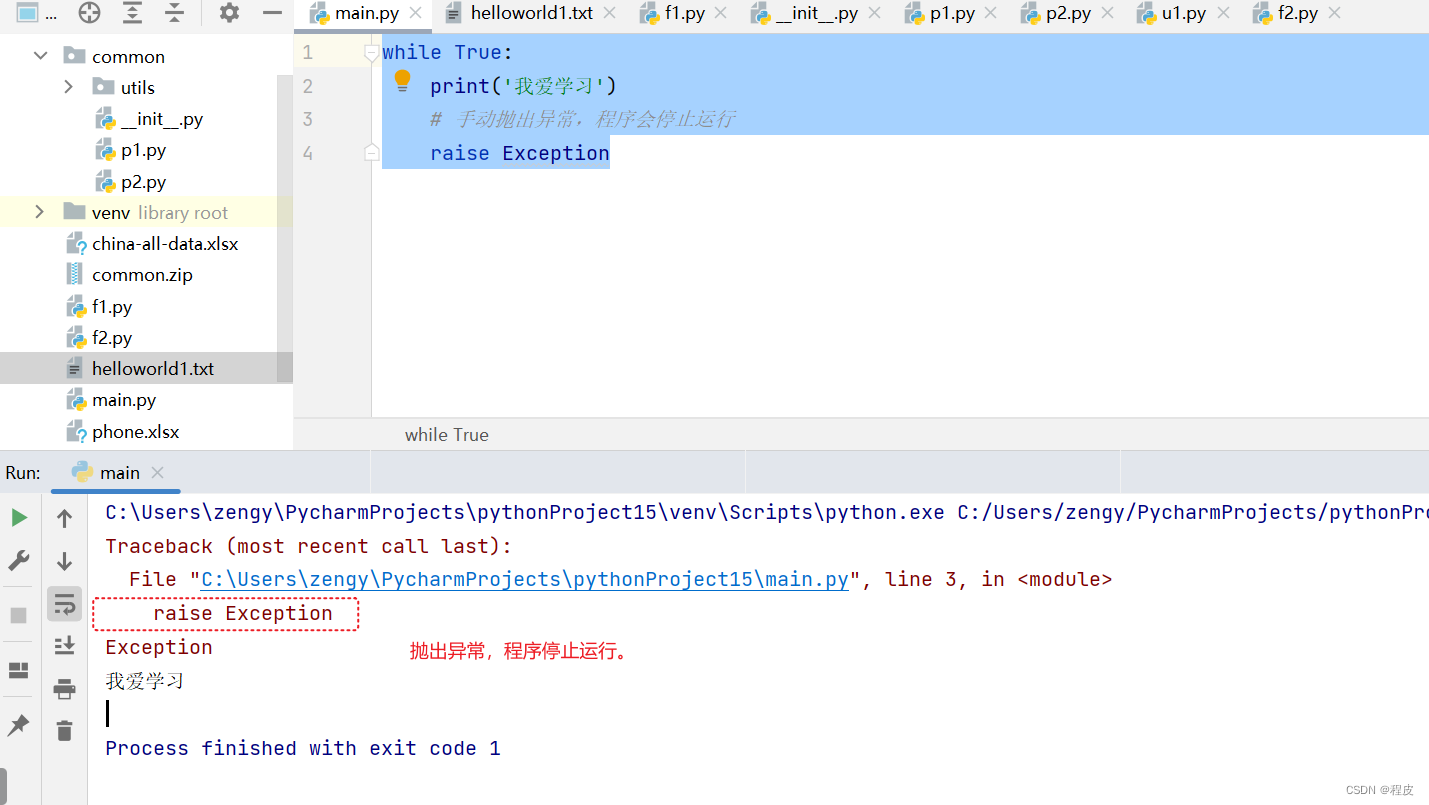
python异常处理
参考语法:https://docs.python.org/zh-cn/3/tutorial/errors.html 在编写代码的时候,如果你写的程序出现报错,程序就会停止运行,后面的代码就不再执行。 如果程序发生错误,可以在代码中添加异常处理,保证程…...

go get命令不再具有安装功能
go get功能呢 一直以来,我们知道go get命令可以借助代码管理工具通过远程拉取或更新代码包及其依赖包,并自动完成编译和安装。整个过程就像安装一个App一样简单。 go get命令可以动态获取远程代码包,命令在内部实际上分成了两步操作&#x…...
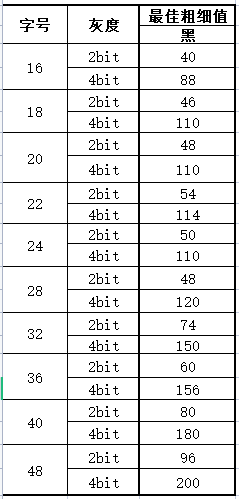
合宙Air724UG LuatOS-Air lvgl7-lvgl(矢量字体)
如何用开发板实现lvgl加载外部矢量字体功能 目录名称 如何用开发板实现lvgl加载外部矢量字体功能 简介材料准备API 说明步骤 1. 将字库芯片接在模块spi上2. 版本定制3. 初始化spi4. 设置字体5.字体使用测试固件和脚本显示效果字号灰度最佳粗细值对应表常见问题 1. 设置68号字体…...

LRU的实现
题目内容 实现一个 LRUCache 类,三个接口: LRUCache(int capacity) 创建一个大小为 capacity 的缓存get(int key) 从缓存中获取键为 key 的键值对的 valueput(int key, int value) 向缓存中添加键值对 (key, value) 要求 get 和 put 的均摊时间复杂度…...

consul 备份还原导入导出
正文 工作中要保证生产环境部署的consul的集群能够安全稳定地对外提供服务,即使出现系统故障也能快速恢复,这里将讲述部分的备份还原操作及KV的导入导出操作。 备份与还原 配置文件、服务器状态 需要备份的主要有两类数据:consul相关的配置文…...
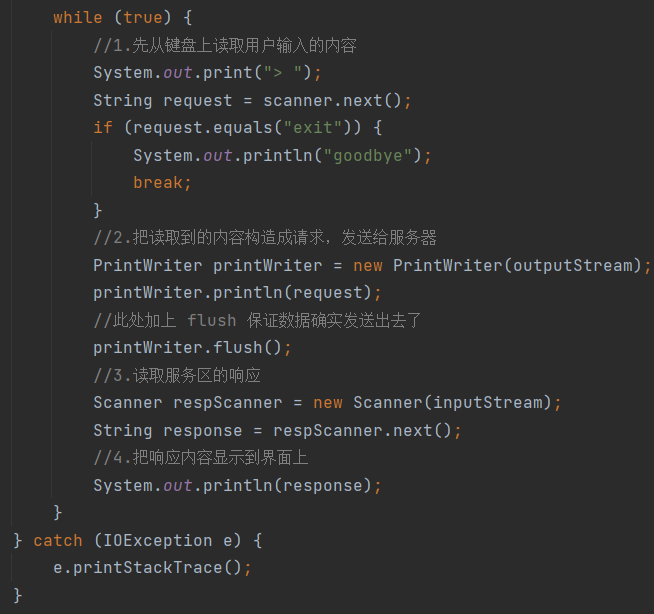
6.网络编程套接字(下)
文章目录 4.TCP流套接字编程4.1ServerSocket API4.2Socket API4.3TCP中的长短连接4.4示例一:一发一收(长连接)4.4.1TCP服务端4.4.2TCP客户端 4.5示例二:请求响应(短连接)4.5.1TCP服务端4.5.2TCP客户端 4.6再…...
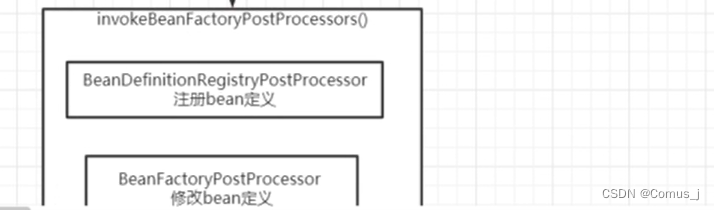
4.3-内置后置PostProcess处理器深度讲解
在reader里面注册了很多Bean定义 reader会调取register()来注册配置类 调用上句,就会把配置类注册到BeanDefinitionMap中去 配置类有了、解析配置类的处理器有了 然后, 在第三步refresh() 进行IOC容器刷新中的invokeBeanPostProcessors(beanFactory…...

LeetCode(力扣)45. 跳跃游戏 IIPython
LeetCode45. 跳跃游戏 II 题目链接代码 题目链接 https://leetcode.cn/problems/jump-game-ii/description/ 代码 class Solution:def jump(self, nums: List[int]) -> int:if len(nums) 1:return 0curdis 0nextdis 0step 0for i in range(len(nums)):nextdis max(…...

mysql5.8 免安装版(压缩包)win10 安装
目录 1、下载MySQL5.82、如何安装、配置my.ini配置注意 3初始化mysql3.1. 初始化mysql3.2. 安装mysql服务3.3. 启动mysql3.4. 登录mysql3.5. 修改root密码3.6. 配置远程连接 Mysql5.8安装踩坑记录,推荐使用Docker安装,我是电脑虚拟化可能会蓝屏没用这个功…...
STM32-HAL库06-硬件IIC驱动FM24CL16B非易失存储器
STM32-HAL库06-IIC驱动FM24CL16B非易失存储器 一、所用材料: STM32VGT6自制控制板 STM32CUBEMX(HAL库软件) MDK5 二、所学内容: 通过HAL库的硬件IIC对FM24CL16B存储器进行写与读取操作。 三、CUBEMX配置: 第一步…...

python-wordcloud词云
导入模块 from wordcloud import WordCloud import jieba import imageio import matplotlib.pyplot as plt from PIL import ImageGrab import numpy as npwordcloud以空格为分隔符号,来将文本分隔成单词 PIL pillow模块 img imageio.imread(image.png)这行代码…...
单元测试与自测
单元测试在百度百科的定义: 自测在百度百科的定义: 单元测试是测一个类或一个函数,自立门第main函数,不依赖于项目,预期的是这个类或函数是没有问题的。程序编码完成之后至各种测试再到用户使用出现的任何bug都是单元测…...

2023-09-12 LeetCode每日一题(课程表 IV)
2023-03-29每日一题 一、题目编号 1462. 课程表 IV二、题目链接 点击跳转到题目位置 三、题目描述 你总共需要上 numCourses 门课,课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ,其中 prerequisites[i] [ai, bi] 表示如果你…...
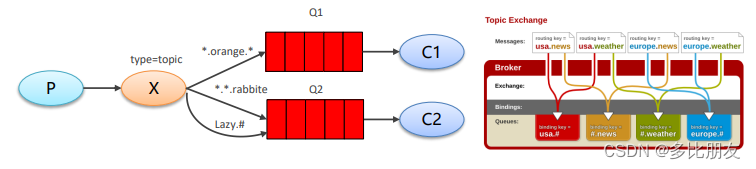
RabbitMQ基础
目录 MQ MQ概述 MQ 的优势 1.应用解耦 2.异步提速 3.削峰填谷 MQ 的劣势 1.系统可用性降低 2.系统复杂度提高 3.一致性问题 使用 MQ 需要满足什么条件呢? RabbitMQ 简介 编辑RabbitMQ 中的相关概念 RabbitMQ 提供了 6 种工作模式 JMS java实现Ra…...
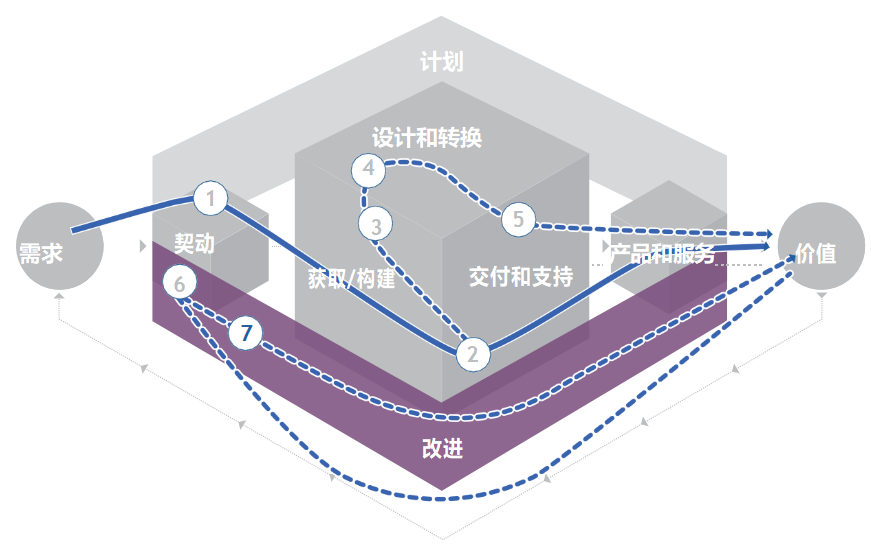
ITIL 4—创建、交付和支持—创建、交付和支持服务的价值流
4. 创建、交付和支持服务的价值流 本章节提供了有关如何: 记录一个价值流以理解工作流程如何贯穿该组织了解创建一个新服务的原型价值流了解支持一个现场服务的原型价值流 本章将帮助从业者理解: 价值流在 服务价值系统(SVS) 中的作用价值流的分类如…...
微信怎么给自己发消息
前段时间看到一份数据调查,说是到目前为止,全球使用微信的用户已达到10亿多人次,天啊,多么强大的用户群体! 这么多人喜欢使用微信,相信大家都知道,微信里面有一个特俗功能,可以自己…...

正交试验设计法
正交实验设计 一、什么是正交试验设计法? 是一种成对测试交互的系统的统计方法。它提供了一种能对所有变量对的组合进行典型覆盖(均匀分布)的方法。 可以从大量的试验点中挑出适量的、有代表性的点,利用“正交表”,…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
