电路电子技术1--关联参考方向及功率的计算
1.判断
电流由元件的低点位端流向高电位端的参考方向称为关联参考方向。(×)
考点:电流、电压的参考方向
解释:在一些复杂的电路中,往往不能预先确定某段电路上的电流、电压的实际方向,所以引进了 “关联参考方向”。为了能够解决问题,可以预先假设一个方向作为分析电路的参考方向,这些假设的电压、电流的方向称为“参考方向”。即,电压、电流的“参考方向”是人为假设的,与实际方向不一定吻合。
而该题中,却以确定的一个电流方向,称为是关联参考方向,所以是错误的。
2.判断
实际电感线圈在任何情况下的电路模型都可以用电感元件来抽象表征。(×)
考点:理想电路元件&电感元件
解释:一个实际电路器件通电后表现出来的电磁性能和能量转换过程往往比较复杂。因此,直接分析不容易入手。我们采用模型化的方法,将实际的电路器件抽象为所谓的理想电路器件。理想电路器件只显示一种主要的电磁现象或物理现象。
之后,我们引进了电路模型,将实际的理想电路器件抽象化为理想电路元件。所谓理想电路元件就是,只反映某一种能量转换过程的元件,其他过程都可以忽略。
而实际的电感线圈并不是在任何情况下都可以当作是理想电路元件。只有当忽略线圈导线中的电阻以及寄生电容时,它才可以成为一个理想的电感元件。
3.填空
电流所经过的路径叫做______,通常由____、____和_____三部分组成。
考点:电路组成的概念
来自课本:简单来说,电路,就是电流流通的路径,其组成部分必须有电源、负载和中间环节。
故依次填写:电路 电源 负载 中间环节
4.填空
考点:在同一个支路中,电流的大小相同,方向相反。
解题:关键是注意到已知的左边的1A,这个1A不仅仅告诉了这个电路中电流的大小为1A,更直接说明了此电路中中电流的方向。 因此:
故以此填空为 -10 -1.
5.选择
考点:一个电路必定处于功率平衡状态,故有元件吸收功率,有元件发出功率。吸收=放出。
解题思路:根据关联参考方向计算功率,若p>0,则元件吸收功率,是耗能的,在电路中的作用为负载。当p<0时,则表示元件发出功率,消耗的电能为负,说明元件产能,在电路中的作用为电源。
对于这个题目,我们可以先假设,假设电压源发出功率,电流源吸收功率,充当负载。 此时:
若电压源发出功率,则电路中电流流向如图所示,电流源的两端的电位如图所示,对于电流源,I、U同方向,P>0,吸收功率。符合。
若我们假设电流源充当电源,发出功率,电压源充当负载,放出功率,则分析如下:
对于电压源,I、U方向相反,P<0(注意题目已给条件I、S均大于0),电压源发出功率,而在一个电路中不可能所有元件都发出功率,所以排除此情况。
故选择A电压源发出功率。6.选择
考点:理解电压源和电流源 来自知乎:可以将电压源、电流源视为控制电压、电流的元件而非提供的元件。 也就是说,电流源只控制自己所在的支路电流,电势差随其他支路变化。电压源只控制自己两端的节点的电势差,电流随其他支路变化。
突破口:因此,我认为这个题开始入手,在于两个节点处的电势差是和电压源两端电势差是相等的。 因此:
因此,该题选择C电阻与电压源各吸收1w功率,电流源提供出2w功率。
相关文章:

电路电子技术1--关联参考方向及功率的计算
1.判断 电流由元件的低点位端流向高电位端的参考方向称为关联参考方向。() 考点:电流、电压的参考方向 解释:在一些复杂的电路中,往往不能预先确定某段电路上的电流、电压的实际方向,所以引进了 “关联参考方向”。为了能够解决问…...
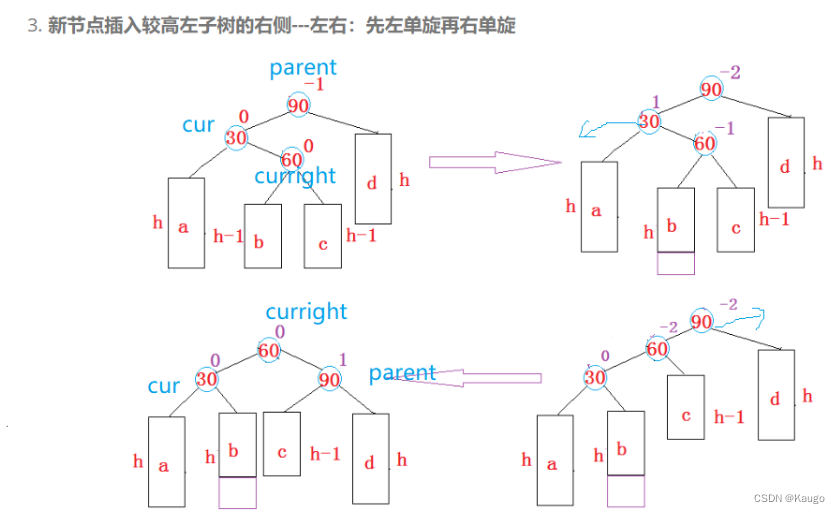
【C++】AVL树的插入操作实现以及验证是否正确(带平衡因子)
文章目录 前言一、AVL树结点的定义二、AVL树的插入(Insert)插入完整代码:1.左单旋(RotateL)2.右单旋(RotateR)3.先右单旋再左单旋(RotateRL)1.保存的bf为02.保存的bf为13…...
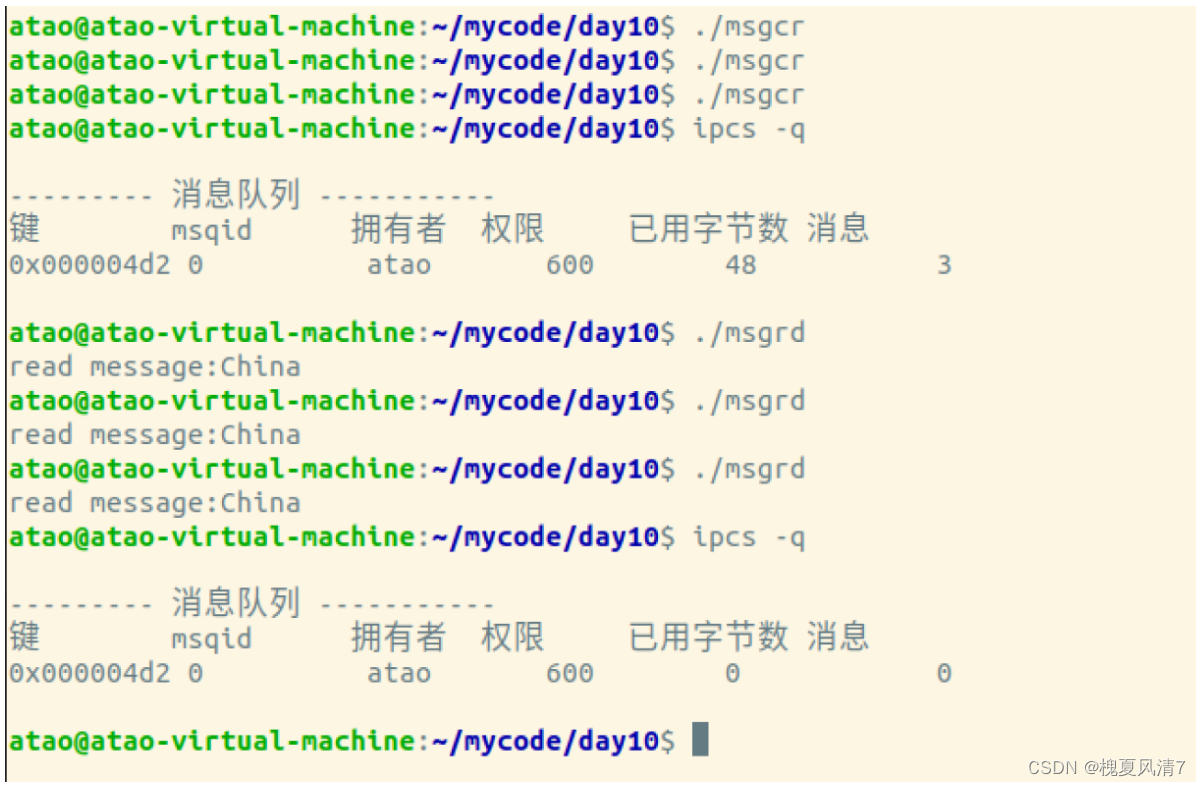
【Linux-Day10-信号量,共享内存,消息队列】
信号量 信号量描述 信号量是一个特殊的变量,一般取正数值。它的值代表允许访问的资源数目,获取资源 时,需要对信号量的值进行原子减一,该操作被称为 P 操作。 当信号量值为 0 时,代表没有资源可用,P 操作…...
使用IntelliJ IDEA本地启动调试Flink流计算工程的2个异常解决
记录:471 场景:使用IntelliJ IDEA本地启动调试Flink流计算时,报错一:加载DataStream报错java.lang.ClassNotFoundException。报错二:No ExecutorFactory found to execute the application。 版本:JDK 1.…...
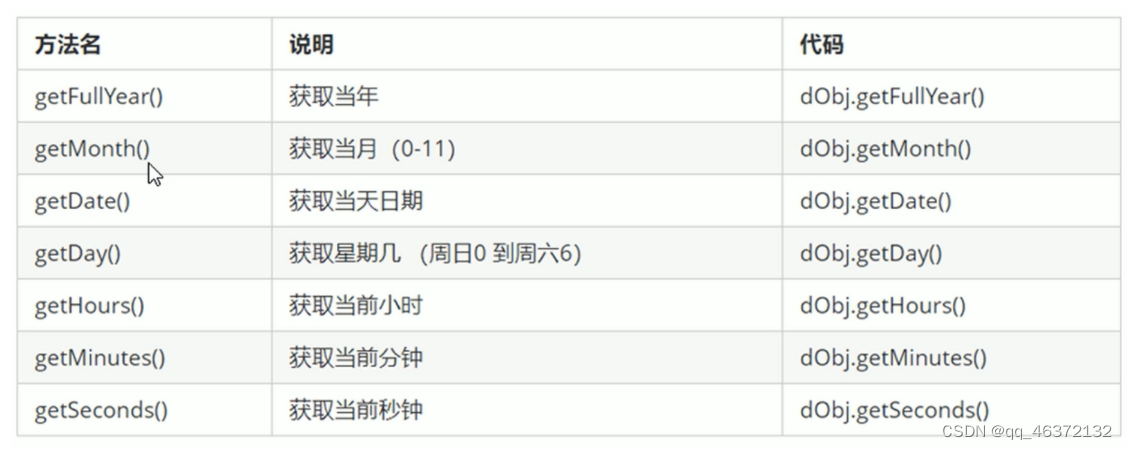
对象及日期对象
对象 1.什么是对象 类是对象的抽象,对象是类的实例 程序算法数据结构 万物皆对象,对象是一个具体的事物,看到见摸得着,对象是一组无序相关属性和方法的集合(无序,所以对象没有length属性),所有事物都是对象,列如字符串,数值,数组,函数等. 属性:事物的特征,在对象中用属性表…...

鼠标滚轮编码器解析
文章目录 前言一、鼠标滚轮编码器逻辑?二、使用步骤 1.引入库2.读入数据总结 前言 鼠标滚轮编码器为三脚接入,一个COM脚C(一般是接地),两个脉冲波形输入脚A、B,转动滚轮编码器会在两个脉冲输入脚上产生脉冲…...
【PTA】攀拓(PAT)- 程序设计(甲级)2023年春季考试
个人学习记录,代码难免不尽人意。 今天又斥资买了今年春季的真题一试,呃,感觉尽力了,89分,在当年排名23,感觉还不错,没有出现读不懂的题目和没有思路的情况,扣的11分分别是第二题两个…...

Spring Cloud Gateway 实现原理
Spring Cloud Gateway是Spring Cloud生态系统中的一个组件,用于构建基于Spring Boot的微服务架构中的网关服务。它的主要目的是提供一种灵活的方式来路由、过滤和转换HTTP请求,从而允许您构建强大、高性能的微服务应用程序。 以下是Spring Cloud Gatewa…...

嘉泰实业:真实低门槛,安全有保障
在互联网金融大行其道的当下,无论用户是多么的青睐、喜爱这种便捷的理财方式,也一定得把资金安全放在心上。要投就投那些实力背景雄厚,诚信经营的平台,可以选择投资用户基数庞大的理财老品牌,也可以选择发展势头迅猛的…...

spring boot 2.7 -> 3.0升级指南
spring boot提供一个版本迁移指南 2.7 -> 3.0...

MQTT 连接优化指南
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

算法和数据结构学习中的一些小的工具函数
算法和数据结构学习中的一些小的工具函数 作者:Grey 原文地址: 博客园:算法和数据结构学习中的一些小的工具函数 CSDN:算法和数据结构学习中的一些小的工具函数 提取一个数二进制最右侧的 1 比如二进制为:0100 0…...

解决2K/4K高分屏下Vmware等虚拟机下Kail Linux界面显示问题
问题现象 在我们日常使用VirtualBox、Vmware workstation、Hyper-V等虚拟机安装使用Kali系统,在2K/4K高分辨率电脑下Kali系统界面显示太小,包括各种软件及命令终端字体均无法很直观的看出,影响我们的正常测试及使用。 常规处理思路 很多人…...

【校招VIP】java语言考点之双亲委派模型
考点介绍: 双亲委派是校招面试中的高频考点之一。双亲委派机制定义: 当一个类加载器收到了类加载的请求的时候,他不会直接去加载指定的类,而是把这个请求委托给自己的父加载器去加载,只有父加载器无法加载这个类的时候࿰…...

2023年阿里云新用户云服务器价格表
阿里云,作为国内领先的云计算服务提供商,一直致力于为全球用户提供安全、稳定、高效的云计算服务。对于新用户来说,阿里云服务器是一个非常不错的选择。那么,阿里云新用户云服务器的价格是怎样的呢?本文将为大家详细介…...

信号相关名词概念汇总-采样周期、泄露、窗函数等
信号相关名词概念汇总-采样周期、泄露、窗函数等 以下为信号相关名词概念的汇总 1 名词解释 采样周期/间隔:采样频率的倒数,两次相邻采样之间的时间间隔采样时间:采样的总时长,即采样点数N和采样周期的乘积采样频率: …...
数字化新零售营销模式如何落地?数字化新零售营销功能推荐
通过科技手段,针对对线下零售店面的客户进行消费行为、频次等的分析,并进一步整合线上线下资源,实现实体零售的效率充分化,便是目前很火的新零售营销模式,能够将实体门店与数字化技术进行有机结合,通过为…...

712. 两个字符串的最小ASCII删除和 -- 动规
712. 两个字符串的最小ASCII删除和 class MinimumDeleteSum:"""712. 两个字符串的最小ASCII删除和https://leetcode.cn/problems/minimum-ascii-delete-sum-for-two-strings/"""def solution(self, s1: str, s2: str) -> int:""&qu…...

python中的小tips
1、注释 1、注释快捷键: Ctrl/ 可以注释掉光标所在的这一行,或者是选中的区域。 对于注释掉的这一行或者这一区域,按下ctrl/则会去掉注释。 2、多行注释 在写多行注释时,英文状态下写三个",会自动变成六个"&…...

高精度(加减乘除)
高精度算法出现的原因 当参与运算的数的范围大大的超出了标准数据类型,如int(-2147483648 ~ 2147483647)或者long long的范围,就需要使用高精度算法来进行数的运算。高精度运算的特点是代码长度比较长,本质是对数学运算…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...






