一阶差分和二阶差分概念及其举例
一阶差分和二阶差分概念及其举例
目录
- 一阶差分和二阶差分概念及其举例
- 1、一阶差分
- 1.1 概念
- 1.2 举例
- 2、二阶差分
- 2.1 概念
- 2.2 举例
1、一阶差分
1.1 概念
一阶差分是指对一个数列中的每个元素,计算其与其前一个元素之差的操作。
1.2 举例
举例来说,对于数列[1, 3, 6, 10, 15,33],它的一阶差分数列可以通过计算每个元素与其前一个元素之差得到。具体计算如下:
差分数列 = [3-1, 6-3, 10-6, 15-10, 33-15] = [2, 3, 4, 5,16]
因此,原数列[1, 3, 6, 10, 15, 33]的一阶差分数列为[2, 3, 4, 5,16]。
2、二阶差分
2.1 概念
二阶差分是指对一个数列进行两次差分操作得到的新数列。在数学中,差分操作是指将数列中的每个元素与它前面的元素之差计算出来,得到一个新的数列。
对于一个数列{ a 1 , a 2 , a 3 , . . . , a n a_1, a_2, a_3, ..., a_n a1,a2,a3,...,an},它的一阶差分可以表示为 { b 1 , b 2 , b 3 , . . . , b n − 1 b_1, b_2, b_3, ..., b_{n-1} b1,b2,b3,...,bn−1},其中 b i = a i + 1 − a i b_i = a_{i+1} - a_i bi=ai+1−ai。再对一阶差分数列进行一次差分操作,得到的就是二阶差分数列 { c 1 , c 2 , c 3 , . . . , c n − 2 c_1, c_2, c_3, ..., c_{n-2} c1,c2,c3,...,cn−2},其中 c i = b i + 1 − b i c_i = b_{i+1} - b_i ci=bi+1−bi。
2.2 举例
假设我们有一个数列 {1, 4, 9, 16, 25,36,49,64},我们可以计算其一阶差分和二阶差分。
一阶差分:
b 1 = a 2 − a 1 = 4 − 1 = 3 b_1 = a_2 - a_1 = 4 - 1 = 3 b1=a2−a1=4−1=3
b 2 = a 3 − a 2 = 9 − 4 = 5 b_2 = a_3 - a_2 = 9 - 4 = 5 b2=a3−a2=9−4=5
b 3 = a 4 − a 3 = 16 − 9 = 7 b_3 = a_4 - a_3 = 16 - 9 = 7 b3=a4−a3=16−9=7
b 4 = a 5 − a 4 = 25 − 16 = 9 b_4 = a_5 - a_4 = 25 - 16 = 9 b4=a5−a4=25−16=9
b 5 = a 6 − a 5 = 36 − 25 = 11 b_5 = a_6 - a_5 = 36 - 25= 11 b5=a6−a5=36−25=11
b 6 = a 7 − a 6 = 49 − 36 = 13 b_6 = a_7 - a_6 = 49 - 36 = 13 b6=a7−a6=49−36=13
b 7 = a 8 − a 7 = 64 − 49 = 15 b_7 = a_8 - a_7 = 64 - 49 = 15 b7=a8−a7=64−49=15
一阶差分数列为 {3, 5, 7, 9,11,13,15}。
二阶差分:
c 1 = b 2 − b 1 = 5 − 3 = 2 c_1 = b_2 - b_1 = 5 - 3 = 2 c1=b2−b1=5−3=2
c 2 = b 3 − b 2 = 7 − 5 = 2 c_2 = b_3 - b_2 = 7 - 5 = 2 c2=b3−b2=7−5=2
c 3 = b 4 − b 3 = 9 − 7 = 2 c_3 = b_4 - b_3 = 9 - 7 = 2 c3=b4−b3=9−7=2
c 4 = b 5 − b 4 = 11 − 9 = 2 c_4= b_5 - b_4 = 11 - 9 = 2 c4=b5−b4=11−9=2
c 5 = b 6 − b 5 = 13 − 11 = 2 c_5 = b_6 - b_5 = 13 - 11 = 2 c5=b6−b5=13−11=2
c 6 = b 7 − b 6 = 15 − 13 = 2 c_6 = b_7 - b_6 = 15 - 13 = 2 c6=b7−b6=15−13=2
二阶差分数列为 {2, 2, 2, 2, 2, 2}。
可以看到,通过两次差分操作,原始数列 {1, 4, 9, 16, 25,36,49,64} 变为二阶差分数列 {2, 2, 2, 2, 2, 2}。
二阶差分常常用于时间序列分析和平滑预测中,可以用来消除原始数列的趋势和季节性变化,从而更好地分析和预测数列的周期性变化。
相关文章:

一阶差分和二阶差分概念及其举例
一阶差分和二阶差分概念及其举例 目录 一阶差分和二阶差分概念及其举例1、一阶差分1.1 概念1.2 举例 2、二阶差分2.1 概念2.2 举例 1、一阶差分 1.1 概念 一阶差分是指对一个数列中的每个元素,计算其与其前一个元素之差的操作。 1.2 举例 举例来说,对…...
使用自定义注解和SpringAOP捕获Service层异常,并处理自定义异常
目录 一 自定义异常二 自定义注解三 注解切面处理类四 使用 一 自定义异常 /*** 自定义参数为null异常*/ public class NoParamsException extends Exception {//用详细信息指定一个异常public NoParamsException(String message){super(message);}//用指定的详细信息和原因构…...
Kotlin(六) 类
目录 创建类 调用类 类的继承------open 构造函数 创建类 创建类和创建java文件一样,选择需要创建的目录New→Kotlin File/Class Kotlin中也是使用class关键字来声明一个类的,这一点和Java一致。现在我们可以在这个类中加入字段和函数来丰富它的功…...
)
蓝桥杯官网练习题(灌溉)
题目描述 小蓝负责花园的灌溉工作。 花园可以看成一个 n 行 m 列的方格图形。中间有一部分位置上安装有出水管。 小蓝可以控制一个按钮同时打开所有的出水管,打开时,有出水管的位置可以被认为已经灌溉好。 每经过一分钟,水就会向四面扩展…...
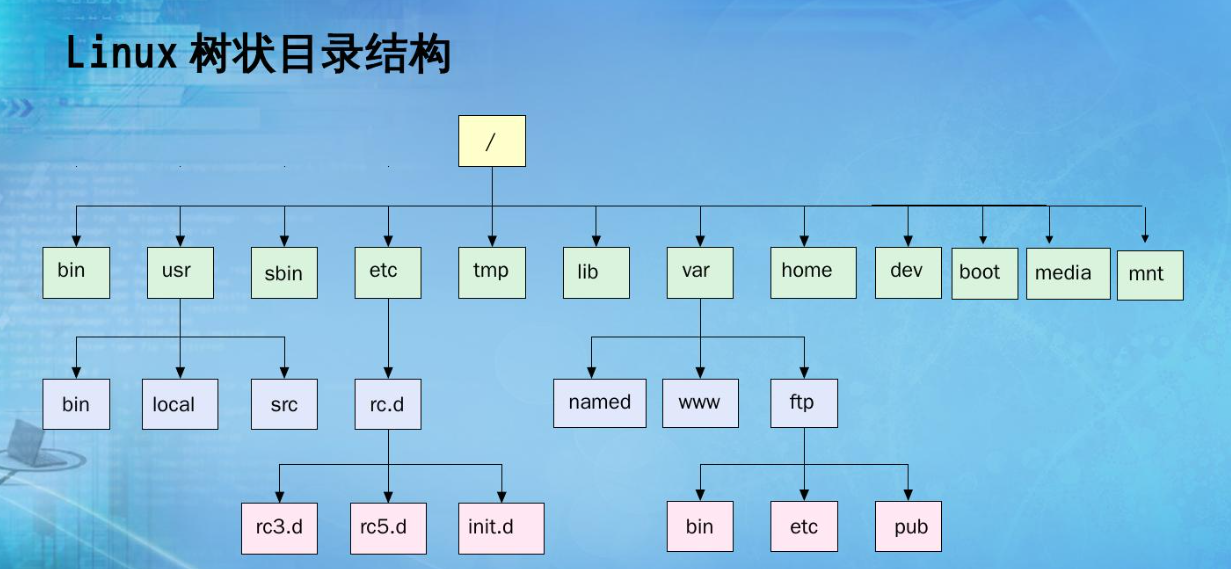
数据结构:树的概念和结构
文章目录 1. 树的概念2. 树的结构3. 树的相关概念4. 树的表示孩子表示法双亲表示法孩子兄弟表示法 5. 树在实际中的应用5. 树在实际中的应用 1. 树的概念 树是一种非线性的数据结构,它是由 n (n > 0)个有限结点组成一个具有层次关系的. 把它叫做树是因为它看起来像一棵倒挂的…...

【GIS】栅格转面报错:ERROR 000864输入栅格: 输入不在定义的属性域内。 ERROR 000863: 无效的 GP 数据类型
问题: 栅格转面(矢量)时,ArcGIS窗口显示:ERROR 000864输入栅格: 输入不在定义的属性域内。 ERROR 000863: 无效的 GP 数据类型. 原因: 栅格转面时输入的栅格数据集的字段必须是整型. 解决办法: 使用Spatial Analyst中的转为整型工具,将栅格数据转为整型后再进行栅格转面的操作…...

32 WEB漏洞-文件操作之文件下载读取全解
目录 介绍利用获取数据库配置文件文件名,参数值,目录符号 涉及案例:Pikachu-文件下载测试-参数Zdns-文件下载真实测试-功能点小米路由器-文件读取真实测试-漏洞RoarCTF2019-文件读取真题复现-比赛百度杯2017二月-Zone真题复现-比赛拓展 下载和读取都差不…...

Linux之history、tab、alias、命令执行顺序、管道符以及exit
目录 Linux之history、tab、alias、命令执行顺序、管道符以及exit history历史命令 格式 参数 修改默认记录历史命令条数 案例 案例1 --- 显示history历史记录中出现次数最高的top10 案例2 --- 增加history显示的时间信息 命令与文件名补全 --- tab 命令别名 格式 案…...

vcomp100.dll丢失怎样修复?5个靠谱的修复方法分享
VCOMP100.DLL 是由微软打造的动态链接库,它对于一些图形密集型应用,例如Photoshop,以及多款知名游戏如巫师3的运行至关重要。 如果操作系统在启动应用程序时无法找到此vcomp100.dll,则会出现vcomp100.dll丢失或未找到错误。 如果D…...
)
Vue3自定义指令(directive)
文章目录 前言一、Vue3指令钩子函数二、自定义指令的两种方式1.局部使用例子1:鉴权例子2:拖拽 2.全局使用例子1:监听宽高指令例子2:监听是否出现在视口 总结 前言 此文章主要讲了vue3中自定义指令的使用,以及一些WebA…...

大数据课程L9——网站流量项目的实时业务处理代码
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握网站流量项目的SparkStreaming代码; ⚪ 掌握网站流量项目的HBaseUtil代码; ⚪ 掌握网站流量项目的MysqlUtil代码; ⚪ 掌握网站流量项目的LogBean代码; ⚪ 掌握网站流量项目的To…...
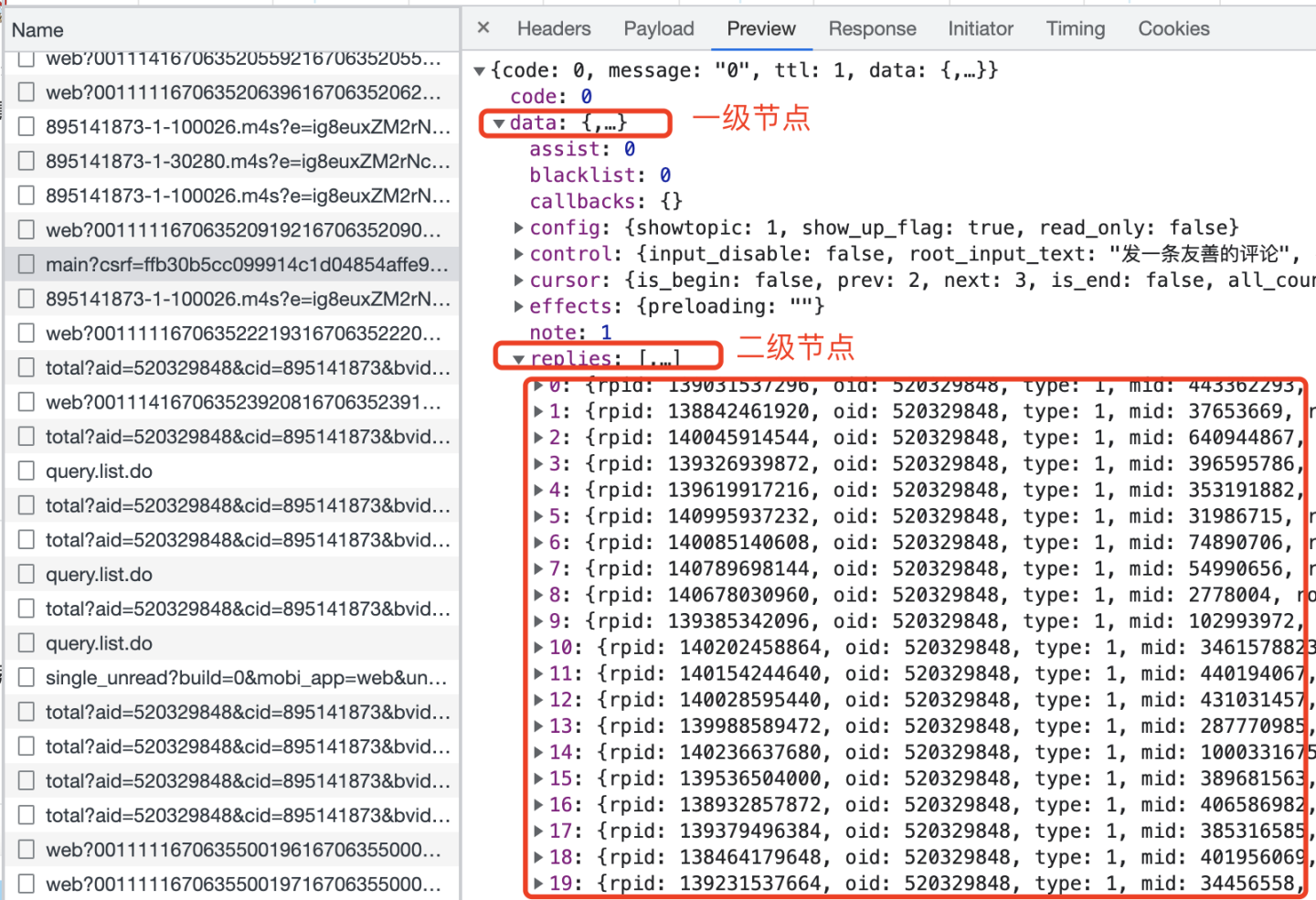
【2023最新B站评论爬虫】用python爬取上千条哔哩哔哩评论
文章目录 一、爬取目标二、展示爬取结果三、爬虫代码四、同步视频五、附完整源码 您好,我是 马哥python说,一枚10年程序猿。 一、爬取目标 之前,我分享过一些B站的爬虫: 【Python爬虫案例】用Python爬取李子柒B站视频数据 【Pyt…...

mysql设置max_sp_recursion_depth,sql_mode
mysql 中设置 @@max_sp_recursion_depth select @@max_sp_recursion_depth; 今天在mysql 写存储过程递归调用时,发现老是报错(recovery limit 0(as set by the max_sp_recursion_depth));后来百度下发现 max_sp_recursion_depth设置不对; 这个修改涉及到全局和session级修…...
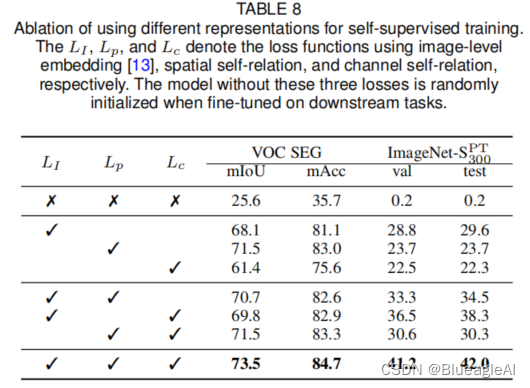
论文阅读:SERE: Exploring Feature Self-relation for Self-supervised Transformer
Related Work Self-supervised 学习目的是在无人工标注的情况下通过自定制的任务(hand-crafted pretext tasks)学习丰富的表示。 Abstract 使用自监督学习为卷积网络(CNN)学习表示已经被验证对视觉任务有效。作为CNN的一种替代…...

遥感数据与作物模型同化应用:PROSAIL模型、DSSAT模型、参数敏感性分析、数据同化算法、模型耦合、精度验证等主要环节
查看原文>>>遥感数据与作物模型同化实践技术应用 基于过程的作物生长模拟模型DSSAT是现代农业系统研究的有力工具,可以定量描述作物生长发育和产量形成过程及其与气候因子、土壤环境、品种类型和技术措施之间的关系,为不同条件下作物生长发育及…...
Navicat15工具连接PostgreSQL15失败
1.错误现象及原因 错误现象: 错误原因: postgresql 15版本中 pg_database 系统表把 datlastsysoid 列删除了,所以造成了此错误。 2.解决方法 (1)将Navicat工具更新到官网最新版本。 (2)更换…...

开源AI家庭自动化助手-手机控制家庭智能家居服务
产品简介 将本地控制和隐私放在首位的开源家庭自动化。由全球开发者和 DIY 爱好者社区提供支持。非常适合在 Raspberry Pi 或本地服务器上运行。 功能介绍 1. 控制面板在控制面板,你可以查看家庭的灯光,温度,门铃,音响…...

解决CSS定位错乱/疑难杂症的终极绝招==》从样式污染开始排查
我们接手他人或者第三方项目的时候,有时候会遇到一些莫名其妙的问题: 明明自己的样式写的没有问题,但是网页上却显示的乱七八糟的,或者效果完全出不来。 案例如下: 这里只用了很典型的flex弹性布局,并没有…...

【笔记】《C++性能优化指南》Ch3 测量性能
【笔记】《C性能优化指南》Ch3 测量性能 1. 优化思想1.1 专业的性能测试流程1.2 优化准则1.2.1 90/10规则1.2.2 Amdahl定律 2. 进行实验2.1 记实验笔记2.2 测量基准性能并设定目标2.3 你只能改善你能够测量的 3. 分析程序执行3.1 实现分析器的方式3.2 分析器的优缺点 4. 测量长…...
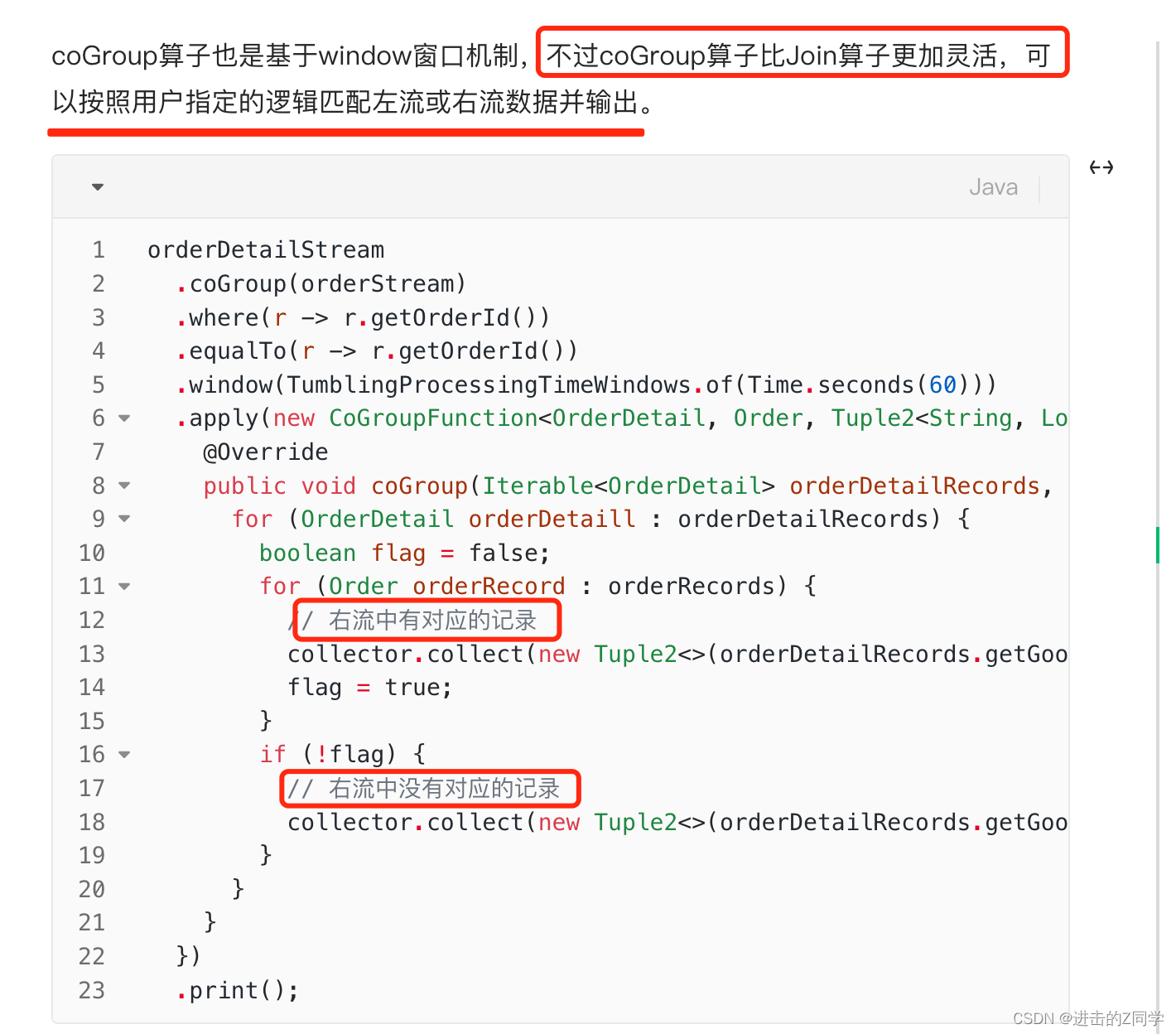
2023大数据面试总结
文章目录 Flink(SQL相关后面专题补充)1. 把状态后端从FileSystem改为RocksDB后,Flink任务状态存储会发生哪些变化?2. Flink SQL API State TTL 的过期机制是 onCreateAndUpdate 还是 onReadAndWrite?3. watermark 到底…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
