6.2.3 【MySQL】InnoDB的B+树索引的注意事项
6.2.3.1 根页面万年不动窝
B+ 树的形成过程是这样的:
- 每当为某个表创建一个 B+ 树索引(聚簇索引不是人为创建的,默认就有)的时候,都会为这个索引创建一个 根节点 页面。最开始表中没有数据的时候,每个 B+ 树索引对应的 根节点 中既没有用户记录,也没有目录项记录。
- 随后向表中插入用户记录时,先把用户记录存储到这个 根节点 中。
- 当 根节点 中的可用空间用完时继续插入记录,此时会将 根节点 中的所有记录复制到一个新分配的页,比如 页a 中,然后对这个新页进行 页分裂 的操作,得到另一个新页,比如 页b 。这时新插入的记录根据键值(也就是聚簇索引中的主键值,二级索引中对应的索引列的值)的大小就会被分配到 页a 或者 页b 中,而根节点 便升级为存储目录项记录的页。
要注意的是:一个B+树索引的根节点自诞生之日起,便不会再移动。这样只要我们对某个表建立一个索引,那么它的 根节点 的页号便会被记录到某个地方,然后凡是 InnoDB 存储引擎需要用到这个索引的时候,都会从那个固定的地方取出 根节点 的页号,从而来访问这个索引。
6.2.3.2 内节点中目录项记录的唯一性
我们知道 B+ 树索引的内节点中目录项记录的内容是 索引列 + 页号 的搭配,但是这个搭配对于二级索引来说有点儿不严谨。还拿 index_demo 表为例,假设这个表中的数据是这样的:
| c1 | c2 | c3 |
| 1 | 1 | 'u' |
| 3 | 1 | 'd' |
| 5 | 1 | 'y' |
| 7 | 1 | 'a' |
如果二级索引中目录项记录的内容只是 索引列 + 页号 的搭配的话,那么为 c2 列建立索引后的 B+ 树应该长这样:
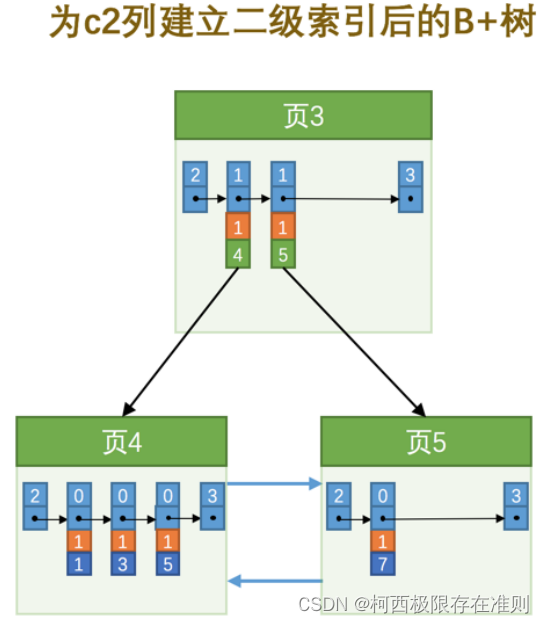
为了让新插入记录能找到自己在那个页里,我们需要保证在B+树的同一层内节点的目录项记录除 页号 这个字段以外是唯一的。所以对于二级索引的内节点的目录项记录的内容实际上是由三个部分构成的:
- 索引列的值
- 主键值
- 页号
也就是我们把 主键值 也添加到二级索引内节点中的目录项记录了,这样就能保证 B+ 树每一层节点中各条目录项记录除 页号 这个字段外是唯一的。
6.2.3.3 一个页面最少存储2条记录
B+树本质上就是一个大的多层级目录,每经过一个目录时都会过滤掉许多无效的子目录,直到最后访问到存储真实数据的目录。InnoDB 的一个数据页至少可以存放两条记录。
6.2.4 MyISAM中的索引方案简单介绍
InnoDB 中索引即数据,也就是聚簇索引的那棵 B+ 树的叶子节点中已经把所有完整的用户记录都包含了,而 MyISAM 的索引方案虽然也使用树形结构,但是却将索引和数据分开存储:
- 将表中的记录按照记录的插入顺序单独存储在一个文件中,称之为 数据文件 。这个文件并不划分为若干个数据页,有多少记录就往这个文件中塞多少记录就成了。我们可以通过行号而快速访问到一条记录。但是在插入数据的时候并没有刻意按照主键大小排序,所以我们并不能在这些数据上使用二分法进行查找。
- 使用 MyISAM 存储引擎的表会把索引信息另外存储到一个称为 索引文件 的另一个文件中。 MyISAM 会单独为表的主键创建一个索引,只不过在索引的叶子节点中存储的不是完整的用户记录,而是 主键值 + 行号 的组合。也就是先通过索引找到对应的行号,再通过行号去找对应的记录!
- 这一点和 InnoDB 是完全不相同的,在 InnoDB 存储引擎中,我们只需要根据主键值对 聚簇索引 进行一次查找就能找到对应的记录,而在 MyISAM 中却需要进行一次 回表 操作,意味着 MyISAM 中建立的索引相当于全部都是 二级索引 !
- 如果有需要的话,我们也可以对其它的列分别建立索引或者建立联合索引,原理和 InnoDB 中的索引差不多,不过在叶子节点处存储的是 相应的列 + 行号 。这些索引也全部都是 二级索引 。
相关文章:

6.2.3 【MySQL】InnoDB的B+树索引的注意事项
6.2.3.1 根页面万年不动窝 B 树的形成过程是这样的: 每当为某个表创建一个 B 树索引(聚簇索引不是人为创建的,默认就有)的时候,都会为这个索引创建一个 根节点 页面。最开始表中没有数据的时候,每个 B 树…...
)
前端面试话术集锦第 12 篇:高频考点(Vue常考基础知识点)
这是记录前端面试的话术集锦第十二篇博文——高频考点(Vue常考基础知识点),我会不断更新该博文。❗❗❗ 这一章节我们将来学习Vue的一些经常考到的基础知识点。 1. 生命周期钩子函数 在beforeCreate钩子函数调用的时候,是获取不到props或者data中的数据的,因为这些数据的…...

骨传导耳机危害有哪些?值得入手吗?
事实上,只要是正常使用,骨传导耳机并不会对身体造成伤害,并且在众多耳机种类中,骨传导耳机可以说是相对健康的一种耳机,这种耳机最独特的地方便是声波不经过外耳道和鼓膜, 而是直接将人体骨骼结构作为传声介…...

网络爬虫-----初识爬虫
目录 1. 什么是爬虫? 1.1 初识网络爬虫 1.1.1 百度新闻案例说明 1.1.2 网站排名(访问权重pv) 2. 爬虫的领域(为什么学习爬虫 ?) 2.1 数据的来源 2.2 爬虫等于黑客吗? 2.3 大数据和爬虫又有啥关系&…...

vue 功能:点击增加一项,点击减少一项
功能介绍: 默认为一列,当点击右侧"" 号,增加一列;点击 “-” 号,将当前列删除; 功能截图: 功能代码: //HTML <el-col :span"24"><el-form-item lab…...

我的编程学习笔记
1. 引言: 在开始编写任何代码之前,都需要理解编程的基本概念。编程是人与计算机进行交流的方式,它让计算机可以理解和执行特定的任务。编程语言是这种交流的工具,而学习编程就是学习如何用特定的语言表达出我们想要的计算机行为。…...

页面静态化、Freemarker入门
页面静态化介绍 页面的访问量比较大时,就会对数据库造成了很大的访问压力,并且数据库中的数据变化频率并不高。 那需要通过什么方法为数据库减压并提高系统运行性能呢?答案就是页面静态化。页面静态化其实就是将原来的动态网页(例如通过ajax…...

PCL (再探)点云配准精度评价指标——均方根误差
目录 一、算法原理二、代码实现三、代码解析四、备注本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、算法原理 见: 点云配准精度评价指标——均方根误差PCL 点云配准精度评价——点到面的均方根误差Open3D(C++) 点…...

【Redis速通】基础知识1 - 虚拟机配置与踩坑
Ubuntu 配置 Redis 下载 redis 找到 redis 官网界面,下载 redis6.2LTS 点击前往 用 mobax 连接到 ubuntu 虚拟机,把下载好的 tar.gz 文件丢到任意一个文件夹下面 进入该文件夹,于此处打开终端,进行解压操作:tar -z…...
我的创作纪念日---从考研调剂到研一的旅程
文章目录 一、前言二、机缘三、收获四、日常五、憧憬 一、前言 大家好,我是小馒头学Python,小馒头学Python就是我,今天是我第一次收到创作纪念日的私信,去年的今天我还在考研,那个时候整天浑浑噩噩的,迷茫…...

Python-实现邮件发送:flask框架或django框架可以直接使用
在项目中,会使用到发送邮件的功能。不同框架的配置可能有所不同,直接写一个不依赖框架配置的邮件发送模块。 使用的功能: 1、可以发送给多个邮箱 2、可以实现抄送多个邮箱 3、可以添加多个文件附件 一、不使用多线程 import smtplib from…...

使用亚马逊云科技Amazon SageMaker,为营销活动制作广告素材
广告公司可以使用生成式人工智能和文字转图像根基模型,制作创新的广告素材和内容。在本篇文案中,将演示如何使用亚马逊云科技Amazon SageMaker从现有的基本图像生成新图像,这是一项完全托管式服务,用于大规模构建、训练和部署机器…...

conda环境安装opencv带cuda版本
主要是cmake编译选项需要修改 以下两个选项按照自己情况修改 -D OPENCV_EXTRA_MODULES_PATH../opencv_contrib/modules \ -D CUDA_TOOLKIT_ROOT_DIR/usr/local/cuda-12.2 \ 其中/home/lixin/anaconda3/envs/stereo 改成你自己的conda环境 cmake -D CMAKE_BUILD_TYPER…...

R语言中的数据结构----矩阵
目录 (1)创建矩阵 (2) 线性代数运算 (3)矩阵索引 (4)矩阵元素的筛选 (5)增加或删除矩阵的行或列 (6)apply()函数 (…...
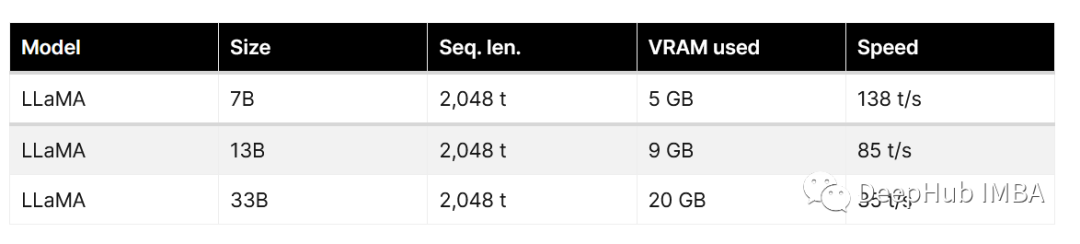
Llama-2 推理和微调的硬件要求总结:RTX 3080 就可以微调最小模型
大语言模型微调是指对已经预训练的大型语言模型(例如Llama-2,Falcon等)进行额外的训练,以使其适应特定任务或领域的需求。微调通常需要大量的计算资源,但是通过量化和Lora等方法,我们也可以在消费级的GPU上…...

C++多线程的用法(包含线程池小项目)
一些小tips: 编译命令如下: g 7.thread_pool.cpp -lpthread 查看运行时间: time ./a.out 获得本进程的进程id: this_thread::get_id() 需要引入的库函数有: #include<thread> // 引入线程库 #include<mutex> //…...
react ant ice3 实现点击一级菜单自动打开它下面最深的第一个子菜单
1.问题 默认的如果没有你的菜单结构是这样的: [{children: [{name: "通用配置"parentId: "1744857774620672"path: "basic"}],name: "系统管理"parentId: "-1"path: "system"} ]可以看到每层菜单的p…...

关于 Qt串口不同电脑出现不同串口号打开失败 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/132842297 红胖子(红模仿)的博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软…...
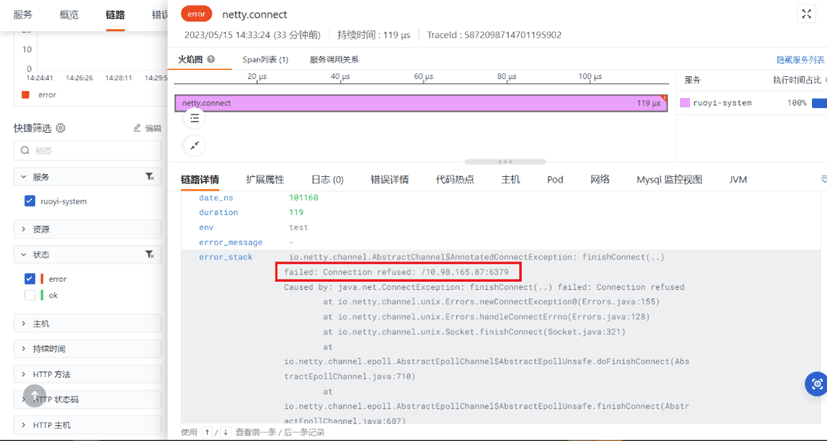
可观测性在灰度发布中的应用
前言 随着云计算的发展、云原生时代的来临,企业数字化转型进程不断深入,应用开发也越来越多地基于微服务化模式,快速迭代的能力使得应用开发更高效、更灵活。同时,也不得不面临应用版本快速升级所带来的的巨大挑战。 传统的发布方…...
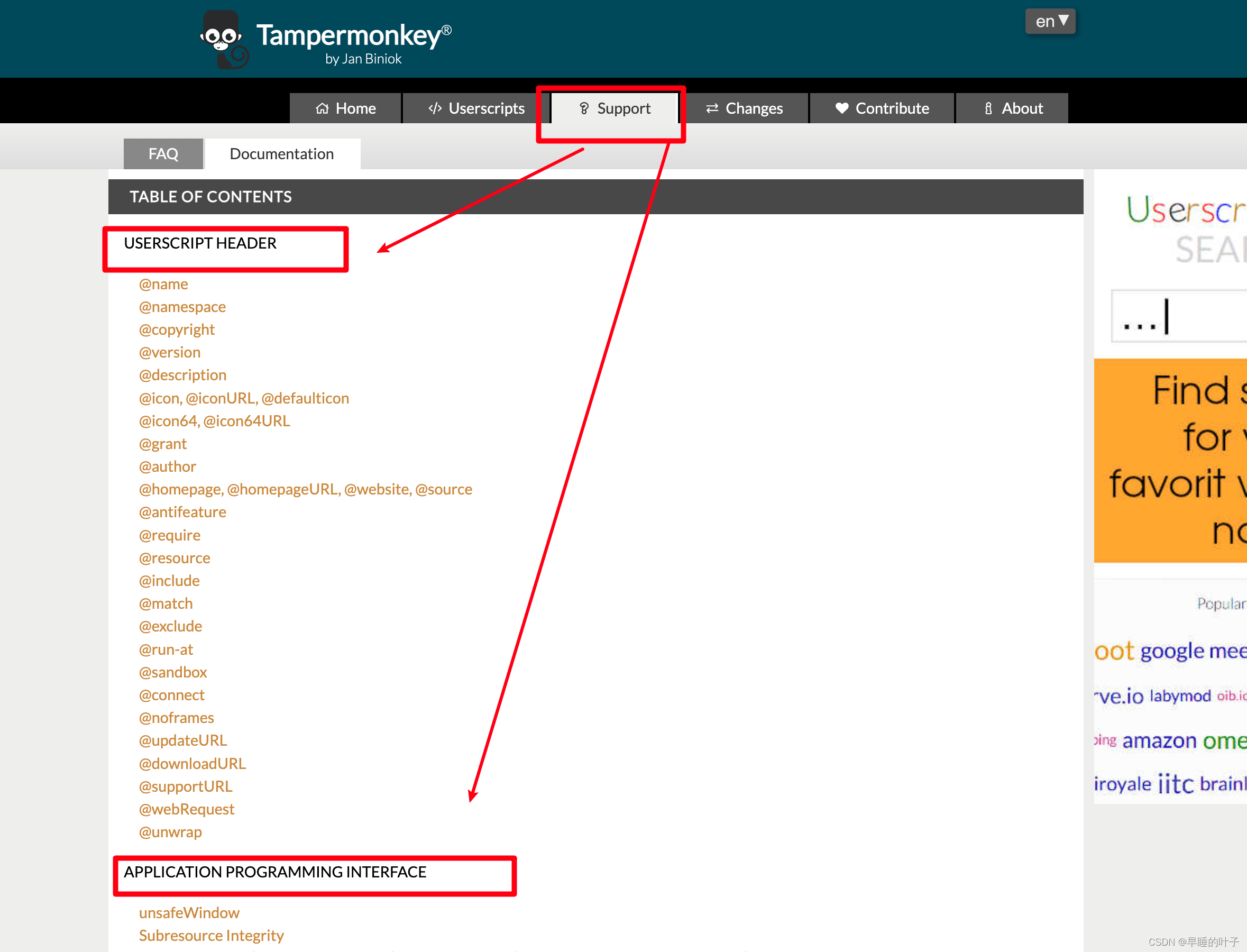
vscode开发油猴插件环境配置指南
文章目录 一、环境配置1.1油猴插件开始编写代码1.2油猴插件配置1.2.1浏览器插件权限1.2.2插件自身权限 2. 油猴脚本API学习2.1 头文件2.2 油猴API 一、环境配置 1.1油猴插件开始编写代码 在vscode 中写入如下代码‘ // UserScript // name cds_test // namespace …...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
