算法前缀和—Java版
前缀和概念
-
假设有数组
A=[1,2,3,4,5,6,7]为原数组,有数组 B作为A的前缀和数组,那么B=[1,3,6,10,15,21,28];可以发现B[i] = A[0]+....+A[i],即B[i]是数组A的前面i个数的总和。可以前缀和表示如下公式:B[i]=∑j=0iA[j]B[i]=\sum_{j=0}^{i}{A[j]} B[i]=j=0∑iA[j]
-
因此有了前缀和数组可以简化我们算法就子区间和,假设没有前缀和要求数组A区间
[2,4]的总和,我们需要从 i=2 遍历 到 i=4 ,时间复杂度为O(n),通过前缀和只需要计算B[4]-B[1]即可,因此可以将子区间和表示如下公式:B[i,j]=B[j]-B[i-1],j>=i 。但是上述子区间表示法在实际应用中会有问题,即当求区间B[0,j]的时候,会出现下标等于-1的情况,因此一般在程序中写成如下:B[i,j]=B[j]−B[i]+A[i]B[i,j]=B[j]-B[i]+A[i] B[i,j]=B[j]−B[i]+A[i]
递推构造前缀和
-
可以使用递推式构造前缀和,递推公式如下:
B[i]=B[i−1]+A[i],B[0]=A[0]B[i]=B[i-1]+A[i],B[0]=A[0] B[i]=B[i−1]+A[i],B[0]=A[0]
不仅仅是这些
- 这些直接求前缀数字和的题目是前缀和最简单的题型,变换题型一般是记录前i个字符或者数组的状态,当遍历后续的i+k时求得前i+k的状态,然后比较两者之间的变化,推出中间长度k子串的状态看看是否满足题目要求。这才是前缀和的灵魂,前缀和一般和数组、子串、连续等关键字有关!!尤其是数组和字符串的问题,求最长子串,求数组满足条件的连续的最长长度!!!通过题目练习总结,尤其是最后两题!
LeetCode
-
560. 和为 K 的子数组
public int subarraySum(int[] nums, int k) {int[] B = new int[nums.length];B[0] = nums[0];int count = 0;for (int i = 1; i < nums.length; i++) {B[i] = B[i-1]+nums[i];}for (int i = 0; i < nums.length; i++) {for (int j = i; j < nums.length; j++) {// 求i到j的前缀和,包括i和jint sum = B[j]-B[i]+nums[i];if(sum==k){count++;}}}return count;} -
525. 连续数组
一般而言,只用前缀和判断区间的复杂度为O(n2),因为遍历区间复杂度就是O(n2),因此,往往使用哈希表来优化问题。前缀和+哈希表!
如下,直接使用前缀和会导致超时!这道题需要把0变成-1,如果前i个数的和为-2,前i+7的和也是-2,那么巧了,那就意味着从i+1到i+7的和为0,即1和-1的数量一样多。这就是前缀的灵魂。public int findMaxLength(int[] nums) {int[] B = new int[nums.length];B[0] = nums[0];for (int i = 1; i < nums.length; i++) {B[i] = B[i-1]+nums[i];}int res = 0;for (int i = 0; i < nums.length; i++) {for (int j = i; j < nums.length; j++) {int sum = B[j]-B[i]+nums[i];if((j-i+1)==sum*2 && sum>res){res = sum;}}}return res;} -
public int findMaxLength(int[] nums) {HashMap<Integer, Integer> map = new HashMap<>();for (int i = 0; i < nums.length; i++) {if(nums[i]==0){nums[i] = -1;}}int[] B = new int[nums.length];B[0] = nums[0];map.put(B[0],0);int maxx = 0;for (int i = 1; i < nums.length; i++) {B[i] = B[i - 1] + nums[i];if(!map.containsKey(B[i])){//只需要存第一个出现的值即可,因为求最长的,所以一定是第一个map.put(B[i],i);}else {//如果前面出现过int value = (i-map.get(B[i]));maxx = Math.max(value,maxx);}if(B[i]==0){maxx = Math.max(i+1,maxx);}}return maxx;}
1685. 有序数组中差绝对值之和
public int[] getSumAbsoluteDifferences(int[] nums) {//使用一个规律,即数组是递增的,即后一个数的和与前一个数的和之间的关系//关系是,假设第i+1个数比第i个数大k,则i+1之后的数会在sum(i)的基础上少// (n-i+1)*k , 而i之前的数会在sum(i)的基础上多 (i-1)*kint n = nums.length;int[] res = new int[n];int sum = 0;for (int i = 0; i < n; i++) {sum+=(Math.abs(nums[i]-nums[0]))}res[0] = sum;for (int i = 1; i < n; i++) {int k = nums[i]-nums[i-1];int a = (i-1)*k;int b = (n-i-1)*k;res[i] = res[i-1]+a-b;}return res;}
1423. 可获得的最大点数
- 一开始秒想到动态规划,但是超时,正确思路是反过来找最小的剩下的连续序列。使用滑动窗口!
public int maxscore(int[] cardPoints,int left,int right,int k){if(k==1 && left<right){int value = Math.max(cardPoints[right],cardPoints[left]);map.put(""+left+right+k,value);return value;}int a = 0;int b = 0;if(map.containsKey(""+(left+1)+right+(k-1))){a = map.get(""+(left+1)+right+(k-1))+cardPoints[left];}else {a = maxscore(cardPoints,left+1,right,k-1)+cardPoints[left];}if(map.containsKey(""+left+(right-1)+(k-1))){b = map.get(""+(left)+(right-1)+(k-1))+cardPoints[right];}else {b = maxscore(cardPoints,left,(right-1),k-1)+cardPoints[right];}return Math.max(a,b);}public int maxScore(int[] cardPoints, int k) {//动态规划map = new HashMap<>();return maxscore(cardPoints,0,cardPoints.length-1,k);}
正确解法:
public int maxScore(int[] cardPoints, int k) {int n = cardPoints.length-k;int[] B = new int[cardPoints.length];B[0] = cardPoints[0];for (int i = 1; i < cardPoints.length; i++) {B[i] = B[i-1]+cardPoints[i];}if(cardPoints.length==k){return B[cardPoints.length-1];}int minn = Integer.MAX_VALUE;for (int i = 0; i <= k; i++) {int sum = B[i+n-1]-B[i]+cardPoints[i];if(sum<minn){minn = sum;}}return B[cardPoints.length-1]-minn;}
1371. 每个元音包含偶数次的最长子字符串
525. 连续数组
-
为什么挂这两道题,因为如果想到了这两道题的前缀和才是真的入门了,首先说525题。这道题前面已经提过,这道题需要把0变成-1,如果前i个数的和为-2,前i+7的和也是-2,那么巧了,那就意味着从i+1到i+7的和为0,即1和-1的数量一样多。这就是前缀的灵魂。那么换成1371,要求五个字母出现都是偶数的最长子字符串的长度,那么5个字符的奇偶状态就有32种,因此,同理在前i个字符如果是 ‘a’,‘e’,‘i’, ‘o’,都是偶数,'u’是奇数,而前i+9个字符前三个是偶数,后两个是奇数,那么意味着什么?意味着从i+1到i+9的子串中有奇数个 ‘o’ 。这只是一个例子,所以需要使用前i+k的状态与前i的状态对比,才知道中间这k个字符是什么状态。因此,前缀和并一定是前面数字之和,也可以是状态的变化。通过后面i+k的状态与i的状态推出中间的状态。这就是前缀和的灵魂。
-
class Solution {public int findTheLongestSubstring(String s) {int n = s.length();int[] pos = new int[1 << 5];Arrays.fill(pos, -1);int ans = 0, status = 0;pos[0] = 0;for (int i = 0; i < n; i++) {char ch = s.charAt(i);if (ch == 'a') {status ^= (1 << 0);} else if (ch == 'e') {status ^= (1 << 1);} else if (ch == 'i') {status ^= (1 << 2);} else if (ch == 'o') {status ^= (1 << 3);} else if (ch == 'u') {status ^= (1 << 4);}if (pos[status] >= 0) {ans = Math.max(ans, i + 1 - pos[status]);} else {pos[status] = i + 1;}}return ans;} }
相关文章:

算法前缀和—Java版
前缀和概念 假设有数组 A[1,2,3,4,5,6,7] 为原数组,有数组 B作为A的前缀和数组,那么B[1,3,6,10,15,21,28];可以发现B[i] A[0]....A[i],即B[i]是数组A的前面i个数的总和。可以前缀和表示如下公式: B[i]∑j0iA[j]B[i]\s…...

拨开迷雾 看见vivo穿越周期的秘密
文|智能相对论作者|佘凯文任何一个行业都有周期性,就好像我们在做股票投资的时候,提到最多的就是周期规律,因为只有掌握规律才可以让我们赚到钱。所以不论是哪家公司都逃脱不了行业周期的宿命。行业寒冬方显强者本色就拿手机行业来说吧&#…...
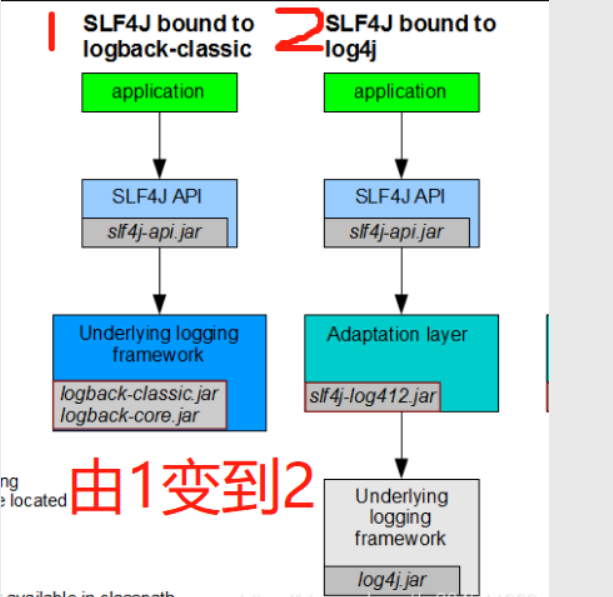
浅谈常用的日志框架
文章目录1.为什么需要日志框架2.常见日志框架2.1.日志框架介绍2.2.市面上的日志框架3.Slf4j使用3.1.如何在系统中使用SLF4j3.2.可能存在的问题4.SpringBoot日志的默认配置5.SpringBoot指定日志文件6.切换日志框架1.为什么需要日志框架 通过日志的方式记录系统运行的过程或错误以…...

字节是真的难进,测开4面终上岸,压抑5个月,终于可以放声呐喊
这次字节的面试,给我的感触很深,意识到基础的重要性。一共经历了五轮面试:技术4面+HR面。 下面看正文 本人自动专业毕业,压抑了五个多月,终于鼓起勇气,去字节面试,下面是我的面试过…...

Bash初识
Bash初识 1.简介: 一.什么是shell? 用过计算机的人知道,我只要点点鼠标计算机就能按照我们的要求来进行相应的操作,那么,你有没有想过计算机为什么能够识别我们的操作呢?俗话说,人有人语,机有机…...
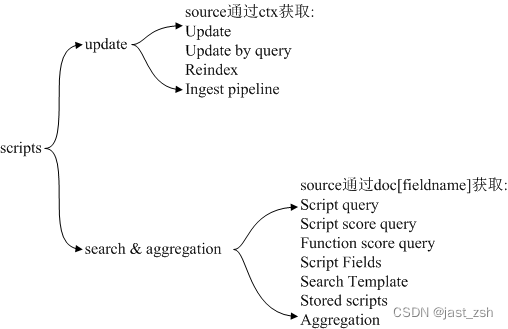
ElasticSearch Script 操作数据最详细介绍
文章目录ElasticSearch Script基础介绍基础用法List类型数据新增、删除nested数据新增、删除根据指定条件修改数据根据指定条件修改多个字段数据-查询条件也使用脚本根据指定条件删除nested中子数据数据根据条件删除数据删除之后结果创建脚本,通过脚本调用根据条件查…...

【黑盒模糊测试】路由器固件漏洞挖掘实战--AFL++ qemu_mode
前言 很久之前就想写AFL++的qemu_mode了,只是模糊测试专题的文章有些过于耗费时间,加上工作原因导致一直搁置。最近需要出差会用到黑盒模糊测试,所以就当做复习一遍,我记得Fuzzing 101也有一个qemu_mode的练习,有空的话下一篇文章更新吧~ 编写不易,如果能够帮助到你,希望…...

【java实现Word模板导出】Xdocreport和Freemaker
如果只是生成简单的word文件的话可以使用 Hutool 上手简单使用方便。 但如果需要导出内容比较复杂的word文件的话用那个就不合适了,这时候就需要Xdocreport这玩意了。 制作模板 新建一个word文档在需要插入变量的地方使用快捷键 Crtl F9 来生成一个域 然后右键单…...

Stable-Baselines 3 部分源代码解读 3 ppo.py
Stable-Baselines 3 部分源代码解读 ./ppo/ppo.py 前言 阅读PPO相关的源码,了解一下标准库是如何建立PPO算法以及各种tricks的,以便于自己的复现。 在Pycharm里面一直跳转,可以看到PPO类是最终继承于基类,也就是这个py文件的内…...
[业务逻辑] 订单超时怎么处理
文章目录1.订单的过程分析2.JDK自带的延时队列 (单机)3.RabbitMQ的延时消息 (消息队列方案)4.RocketMQ的定时消息 (消息队列方案)5.Redis过期监听 (Redis方案)6.定时任务分布式批处理 (扫表轮训方案)7.总结1.订单的过程分析 一个订单流程中有许多环节要用到超时处理 买家超时未…...
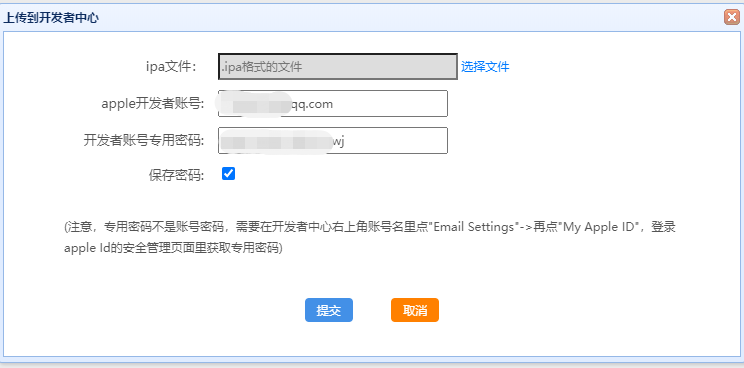
iOS上架及证书最新创建流程
目前使用uniapp框架开发app,大大节省了我们兼容多端应用的工作量和人手,所以目前非常缺乏ios上架和证书创建流程流程的文档假如你没有任何的打包或上架经验,参考本文有很大的收益。通常申请ios证书和上架ipa应用,是需要MAC电脑的&…...

python入门
Python是一种高级编程语言,由荷兰计算机科学家Guido van Rossum于1991年发明。Python语言具有简洁、清晰和易于阅读的语法,同时也拥有广泛的应用领域,包括Web开发、数据分析、人工智能、科学计算等。Python的特点是能够快速开发原型和简单易读…...
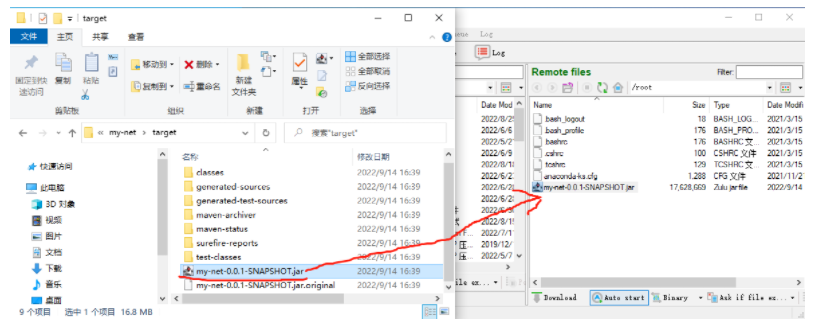
Linux部署java项目
Linux部署java项目启动虚拟机这部分的操作之前学习虚拟机时已经做过,可以参照之前的笔记即可推荐大家重新解压纯净版的RockyLinux来实现启动后登录rockylinuxsudo su -修改root用户密码passwd下面就切换到客户端软件连接虚拟机ifconfigifconfig | more查看ip地址使用Bvssh软件连…...

elisp 从简单实例开始.
elisp 从简单实例开始. 我们怎样用elisp 与电脑交互,先从简单实例开始, 逐渐掌握它的几个对象. 与电脑交互,总要有输入,输出,先看两个简单例子. 输入从minibuffer,输出可以是minibuffer 或者缓冲区. 一: 从minibuffer 中输入, 在指定缓冲中插入文字(insert)x ;;;;;;;;;;;;;;;;…...

ThreeJS加载geojson数据实现3D地图
ThreeJS加载geojson数据实现3D地图,主要通过借助geojson地理信息数据转摩托尔坐标实现,中间借助了d3.js的地图处理方法,最后通过threejs渲染到页面上: 通过平台获取GeoJson格式的行政区域借助d3的方法,将坐标系转摩托尔坐标利用ThreeJS中的自定义Shape,绘制地图利用Three…...
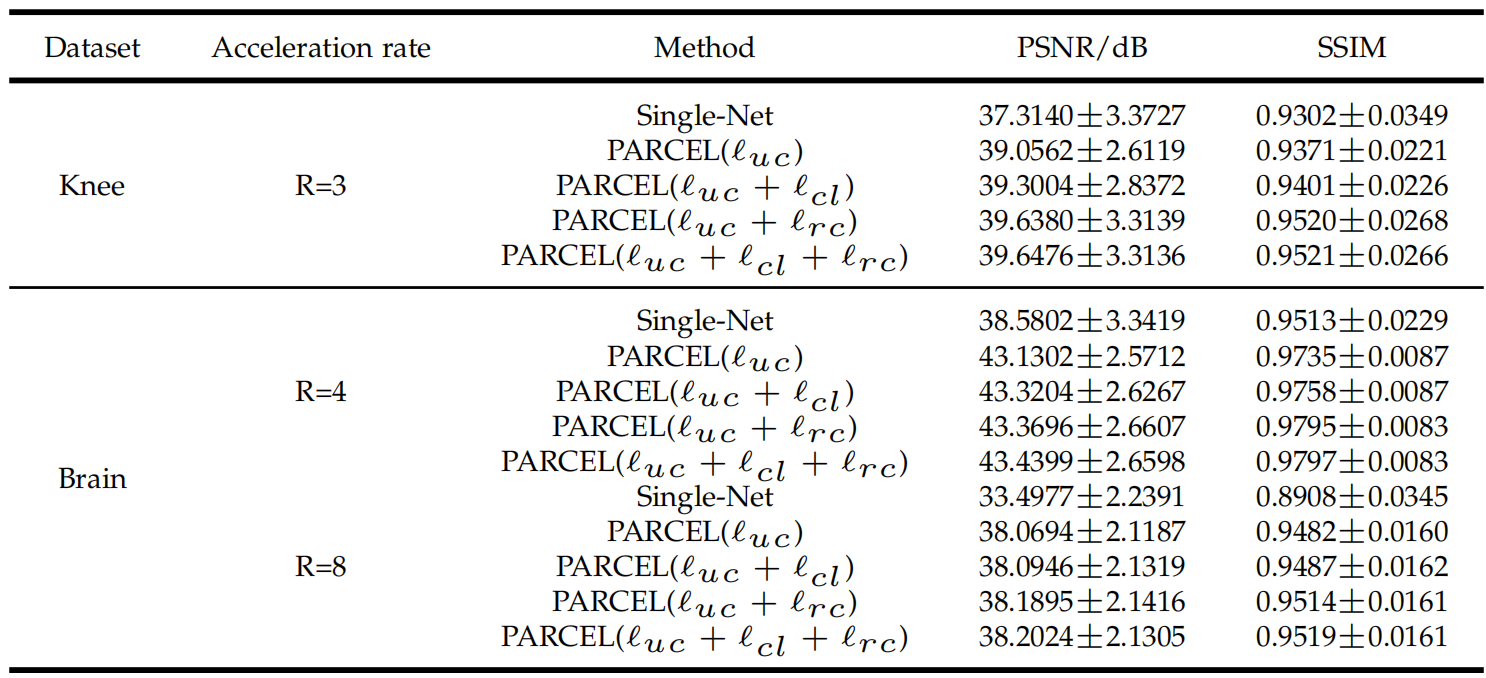
深度学习无监督磁共振重建方法调研(二)
深度学习无监督磁共振重建方法调研(二)Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data(Magnetic Resonance in Medicine 2020)模型设计实验结果PARCEL: Physi…...
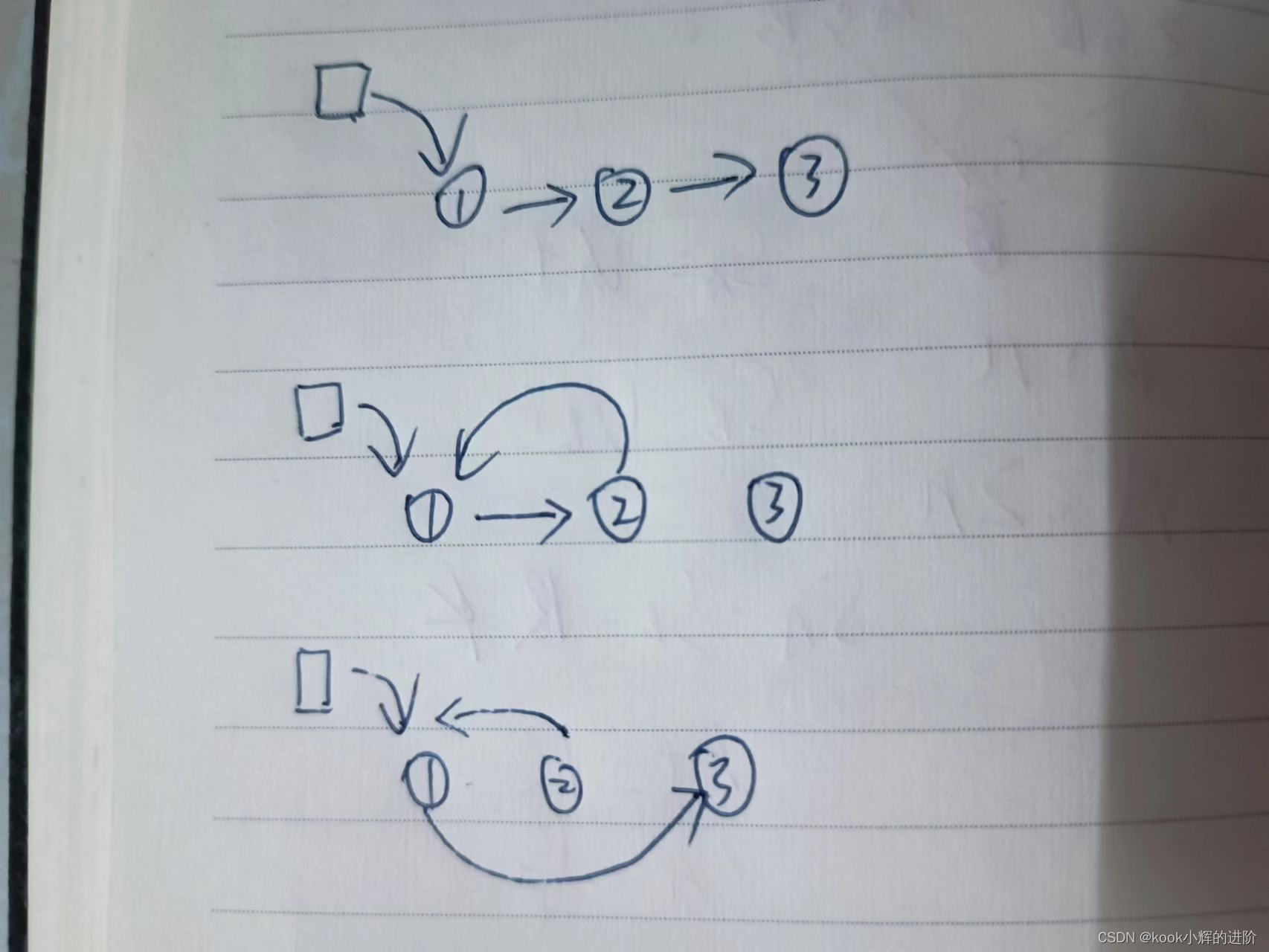
蓝桥杯入门即劝退(十九)两两交换链表
-----持续更新蓝桥杯入门系列算法实例-------- 如果你也喜欢Java和算法,欢迎订阅专栏共同学习交流! 你的点赞、关注、评论、是我创作的动力! -------希望我的文章对你有所帮助-------- 一、题目描述 给你一个链表,两两交换其中…...

【Java 面试合集】接口以及抽象类
接口以及抽象类 1. 概述 嗨,【Java 面试合集】又来了,今天给大家分享的内容是接口以及抽象类。一看这个概念很多人都知道,但是方方面面的细节不一定知道哦,今天我们就从方方面面的细节来讲讲 2. 相同点: 都是上层的抽…...

LeetCode 2391. 收集垃圾的最少总时间
给你一个下标从 0 开始的字符串数组 garbage ,其中 garbage[i] 表示第 i 个房子的垃圾集合。garbage[i] 只包含字符 ‘M’ ,‘P’ 和 ‘G’ ,但可能包含多个相同字符,每个字符分别表示一单位的金属、纸和玻璃。垃圾车收拾 一 单位…...

【PMP考试最新解读】第七版《PMBOK》应该如何备考?(含最新资料)
PMP新版大纲加入了ACP敏捷管理的内容,而且还不少,敏捷混合题型占到了 50%,前不久官方也发了通知8月启用第七版《PMBOK》,大家都觉得考试难度提升了,我从新考纲考完下来,最开始也被折磨过一段时间࿰…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
