Acwing 3534. 矩阵幂 3535. C翻转
3534. 矩阵幂 - AcWing题库
思路:模拟,当然,k次幂可以用快速幂优化,这里懒了
#include <iostream>
#include <vector>
using namespace std;vector<vector<int>> mul(int n, vector<vector<int>>& a, vector<vector<int>>& b) {vector<vector<int>> tmp(n, vector<int>(n, 0));for(int i = 0; i < n; i++) {for(int j = 0; j < n; j++) {int cur = 0;for(int k = 0; k < n; k++) {cur += a[i][k] * b[k][j];}tmp[i][j] = cur;}}return tmp;
}int main() {int n, k;cin >> n >> k;vector<vector<int>> g(n, vector<int>(n));for(int i = 0; i < n; i++) {for(int j = 0; j < n; j++) {cin >> g[i][j];}}vector<vector<int>> res = g;while(--k) {res = mul(n, g, res);}for(int i = 0; i < n; i++) {for(int j = 0; j < n; j++) {cout << res[i][j] << " ";}cout << endl;}return 0;
}3535. C翻转 - AcWing题库
思路:
顺时针旋转[i][j]-->[c+j-d][d+b+c-i-1]
逆时针旋转[i][j]-->[d+b+c-j-1][d+i-c]
#include<iostream>
using namespace std;
int pre[6][6];
int pro[6][6];
int main(){for(int i=1;i<=5;i++){for(int j=1;j<=5;j++){cin>>pre[i][j];}}int a,b,c,d;cin>>a>>b>>c>>d;int n=b;if(a==1){for(int i=c;i<=c+b-1;i++){for(int j=d;j<=d+b-1;j++){pro[c+j-d][d+b+c-i-1]=pre[i][j];}}for(int i=c;i<=c+b-1;i++){for(int j=d;j<=d+b-1;j++){pre[i][j]=pro[i][j];}}}else if(a==2){for(int i=c;i<=c+b-1;i++){for(int j=d;j<=d+b-1;j++){pro[d+b+c-j-1][i+d-c]=pre[i][j];}}for(int i=c;i<=c+b-1;i++){for(int j=d;j<=d+b-1;j++){pre[i][j]=pro[i][j];}}}for(int i=1;i<=5;i++){for(int j=1;j<=5;j++){cout<<pre[i][j]<<" ";}cout<<endl;}return 0;
}相关文章:

Acwing 3534. 矩阵幂 3535. C翻转
3534. 矩阵幂 - AcWing题库 思路:模拟,当然,k次幂可以用快速幂优化,这里懒了 #include <iostream> #include <vector> using namespace std;vector<vector<int>> mul(int n, vector<vector<int>…...

Spring Cloud:构建微服务的最佳实践
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

时间序列场景下多种数据填充算法实践与对比分析
在时间序列建模任务中,模型往往对于缺失数据是比较敏感的,大量的缺失数据甚至会导致训练出来的模型完全不可用,在我前面的博文中也有写到过数据填充相关的内容,感兴趣的话可以自行移步阅读即可: 《python 基于滑动平均…...

Mysql开启binlog
本案例基于mysql5.7.16实验 1、在linux中进入mysql查询binlog是否打开,执行命令如下: mysql -u root -p 2、查询binlog是否开启命令如下,如果log_bin为OFF则证明mysql的binlog没有打开 show variables like %log_bin%; 3、退出mysql终端&…...
【Java Web】HTML 标签 总结
目录 1.HTML 2.标签 1. head 标签 1.图标 2.样式居中 2. body 标签 1.注释 : 2.加载图片 3.加载视频 效果 4.区域 效果 5.上下跳转,页面跳转 效果 6.表格 效果 7.有序列表,无序列表 效果 8.登录 效果 9.按钮 10.多选框…...

前端面试的话术集锦第 4 篇:进阶篇下
这是记录前端面试的话术集锦第四篇博文——进阶篇下,我会不断更新该博文。❗❗❗ 1. 浏览器Eventloop和Node中的有什么区别 众所周知JS是⻔⾮阻塞单线程语⾔,因为在最初JS就是为了和浏览器交互⽽诞⽣的。 如果JS是⻔多线程的语⾔话,我们在多个线程中处理DOM就可能会发⽣问…...
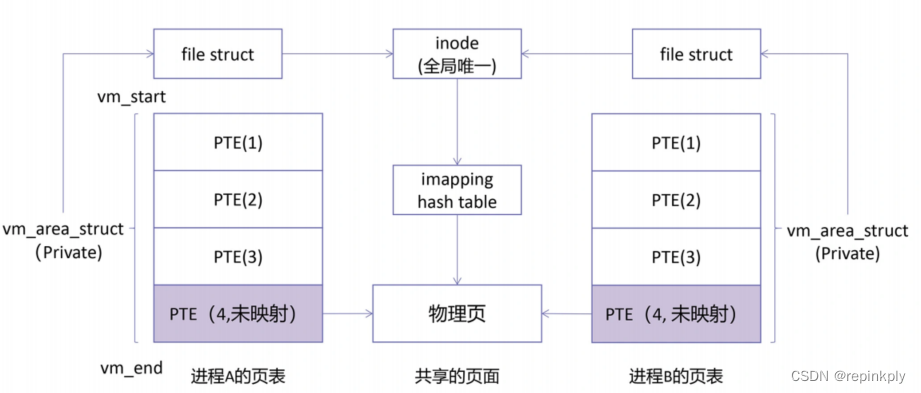
mmap详解
想写一篇文章,详细的介绍一下mmap,主要是原理、用法、mmap泄露来进行介绍。说到mmap,首先得从堆空间说起。 申请堆空间 其实,不管是 32 位系统还是 64 位系统,内核都会维护一个变量 brk,指向堆的顶部&…...
项目02—基于keepalived+mysqlrouter+gtid半同步复制的MySQL集群
文章目录 一.项目介绍1.拓扑图2.详细介绍 二.前期准备1.项目环境2.IP划分 三. 项目步骤1.ansible部署软件环境1.1 安装ansible环境1.2 建立免密通道1.3 ansible批量部署软件1.4 统一5台mysql服务器的数据 2.配置基于GTID的半同步主从复制2.1 在master上安装配置半同步的插件,再…...

【EI征稿】第二届机械电子工程与人工智能国际学术会议(MEAI 2023)
第二届机械电子工程与人工智能国际学术会议(MEAI 2023) The 2nd International Conference on Mechatronic Engineering and Artificial Intelligence 2023年第二届机械电子工程与人工智能国际学术会议(MEAI 2023)计划将于2023年…...

ros2 学习launch文件组织工程 yaml配置文件
简单范例 功能描述 使用launch文件,统一管理工程,实现img转点云,发送到img_pt的topic,然后用reg_pcl节点进行subscribe,进行点云配准处理,输出融合后的点云到map_pt的topic。最后由rviz2进行点云展示。 …...

奇舞周刊第 505 期:实践指南-前端性能提升 270%!
记得点击文章末尾的“ 阅读原文 ”查看哟~ 下面先一起看下本期周刊 摘要 吧~ 奇舞推荐 ■ ■ ■ 实践指南-前端性能提升 270% 当我们疲于开发一个接一个的需求时,很容易忘记去关注网站的性能,到了某一个节点,猛地发现,随着越来越多…...
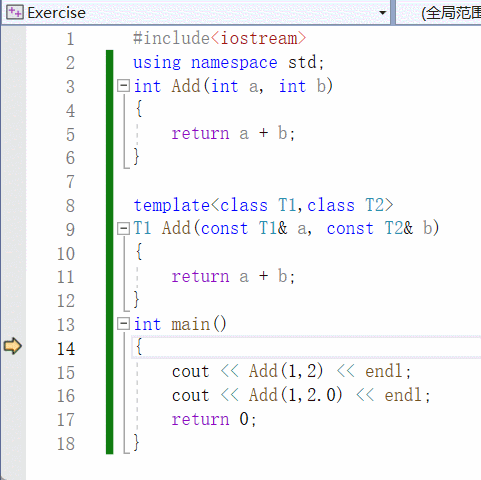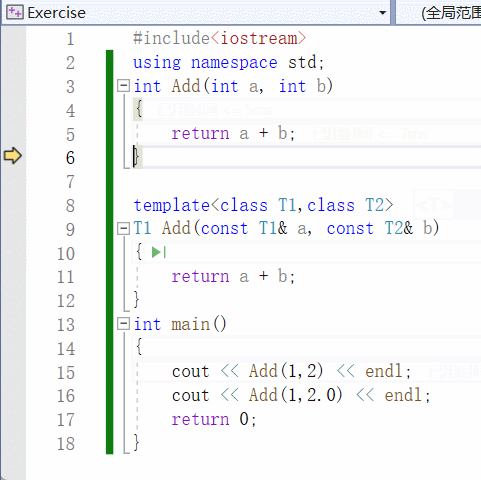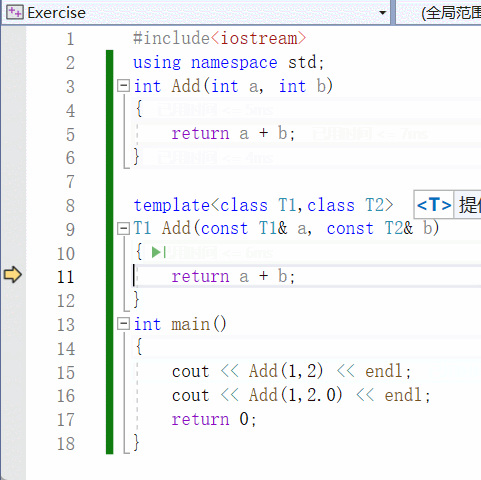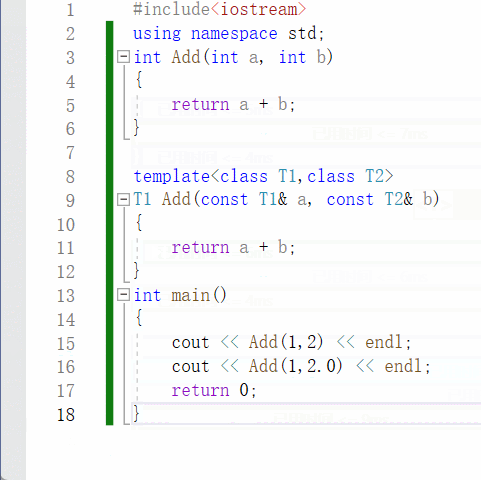
【C++】泛型编程 | 函数模板 | 类模板
一、泛型编程 泛型编程是啥? 编写一种一般化的、可通用的算法出来,是代码复用的一种手段。 类似写一个模板出来,不同的情况,我们都可以往这个模板上去套。 举个例子: void Swap(int& a, int& b) {int tmp …...

web前端——简单的网页布局案列
✨博主:命运之光 🌸专栏:Python星辰秘典 🐳专栏:web开发(简单好用又好看) ❤️专栏:Java经典程序设计 ☀️博主的其他文章:点击进入博主的主页 目录 问题背景 解决样例 …...
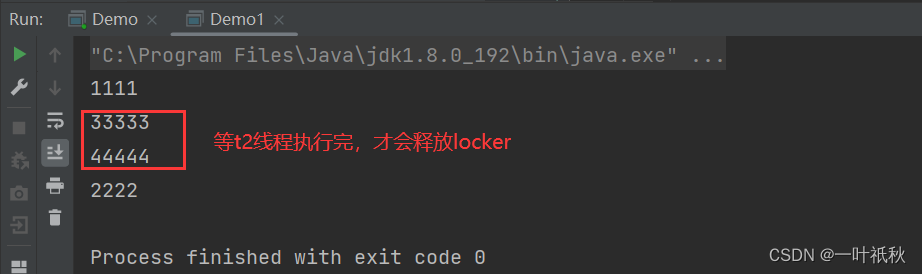
线程安全问题(3)--- wait(),notify()
前言 在多线程的环境下,我们常常要协调多个线程之间的执行顺序,而为了实现这一点,Java提供了一些方法来帮助我们完成这一点。 一,wait() 作用: 使当前线程进入等待状态 释放当前的锁 (即该方法必须和 synchrnized 关键…...
)
【Android知识笔记】进程通信(一)
一、Android Framework 用到了哪些 IPC 方式 Linux 的 IPC 方式有: 管道Socket共享内存信号信号量消息队列管道通信 管道是基于pipefs文件系统实现的,也就是多个进程通过对同一个文件进行读写来实现进程间通信。半双工,单向的,通过 pipe(fds) 系统函数调用可得到一对文件描…...

存储空间压缩6倍 ,多点DMALL零售SaaS场景降本实践
🧑💼 作者简介 冯光普:多点 DMALL 数据库团队负责人,负责数据库稳定性建设与 DB PaaS 平台建设,在多活数据库架构、数据同步方案等方面拥有丰富经验。 杨家鑫:多点高级 DBA,擅长故障分析与性能…...

BGP路由属性
任何一条BGP路由都拥有多个路径属性(Path Attributes),当路由器通告BGP路由给它的对等体时,该路由将会携带多个路径属性,这些属性描述了BGP路由的各项特征,同时在某些场景下也会影响BGP路由优选的决策。 一…...

Java面试常用函数
1. charAt() 方法用于返回字符串指定索引处的字符。索引范围为从 0 到 length() - 1。 map.getOrDefault(num, 0) :如果map存在num这个key,则返回num对应的value,否则返回0. Arrays.sort(nums); 数组排序 Arrays.asList("a","b",&q…...
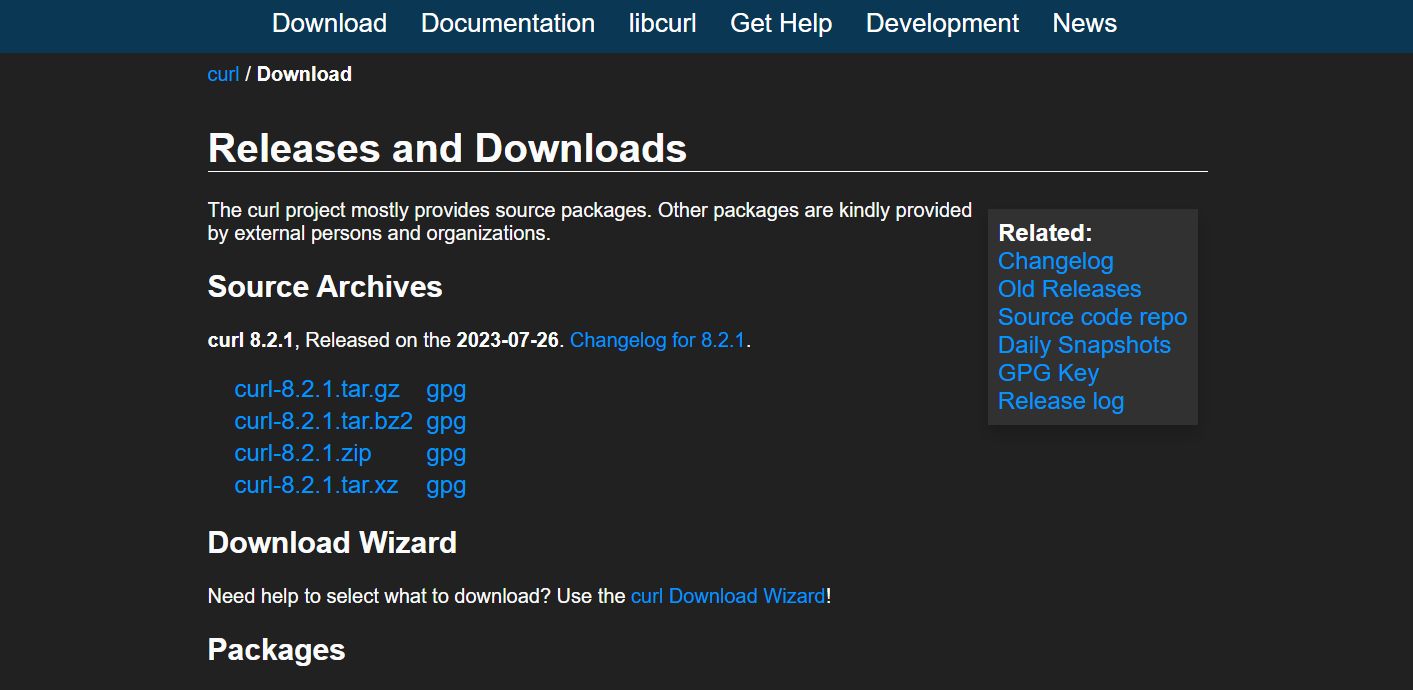
linux编译curl库(支持https)
openssl下载和编译 https://www.openssl.org/source/old/ 解压 tar -xvf openssl-3.0.1.tar.gz cd openssl-3.0.1/配置 ./config如果是编译静态库加入 -fPIC no-shared 如果指定安装路径,使用 --prefix=/usr/local/openssl/选项指定特定目录 编译和安装 make sodu make i…...
)
Ei Scopus检索 | 2024年第三届能源与环境工程国际会议(CFEEE 2024)
会议简介 Brief Introduction 2024年第三届能源与环境工程国际会议(CFEEE 2024) 会议时间:2024年9月1日-3日 召开地点:新西兰奥克兰 大会官网:https://www.cfeee.org/ 2024年第三届能源与环境工程国际会议(CFEEE 2024) 将于2024年12月12日至1…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
