二叉树顺序存储结构
目录
1.二叉树顺序存储结构
2.堆的概念及结构
3.堆的相关接口实现
3.1 堆的插入及向上调整算法
3.1.1 向上调整算法
3.1.2 堆的插入
3.2 堆的删除及向下调整算法
3.2.1 向下调整算法
3.2.2 堆的删除
3.3 其它接口和代码实现
4.建堆或数组调堆的两种方式及复杂度分析
4.1 向上调整建堆
4.1.1 建堆步骤
4.1.2 代码实现
4.1.3 时间复杂度分析 --- O(N*logN)
4.2 向下调整建堆
4.2.1 建堆步骤
4.2.2 代码实现
4.2.3 时间复杂度分析 --- O(N)
5.堆的应用
5.1 堆排序(假设升序)
5.1.1 堆排序步骤
5.1.2 代码实现
5.2 TopK问题
5.2.1 TopK解决步骤
5.2.2 代码实现(数据从文件读取)
1.二叉树顺序存储结构
顺序存储结构就是用数组来存储,一般是用数组只适合来表示完全二叉树,因为不是完全二叉树会有空间浪费的现象。
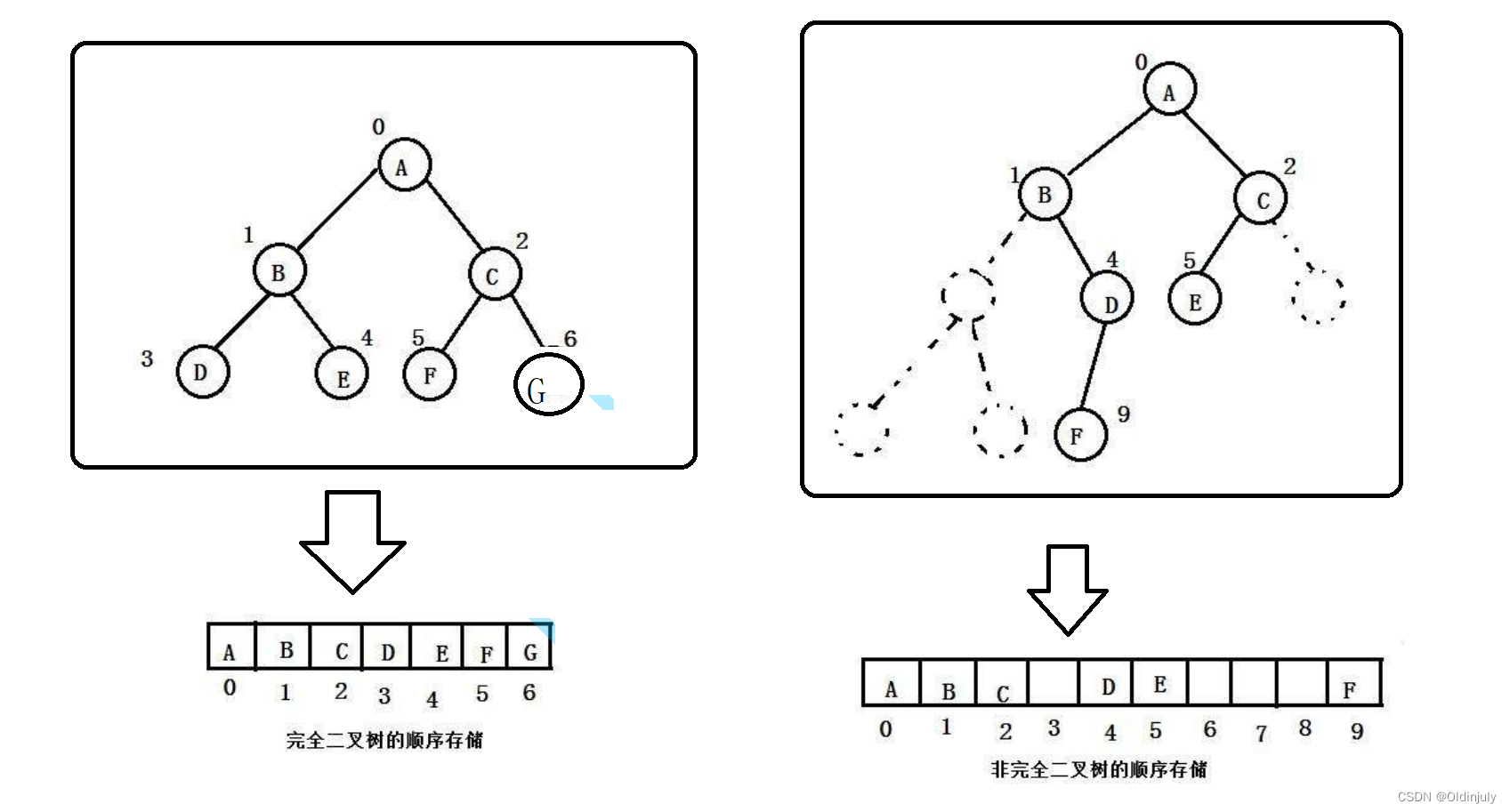
二叉树的顺序存储结构在物理上是一个数组,在逻辑上是一个二叉树。
现实中我们通常把堆使用顺序存储结构的数组来存储,而什么又是堆呢?
需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
2.堆的概念及结构
其实堆就是一个完全二叉树,堆中的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并且满足:堆中某个结点的值总是不大于其父节点的值(大堆)或者堆中某个结点的值总是不小于其父节点的值(小堆)。
总结来说:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树;
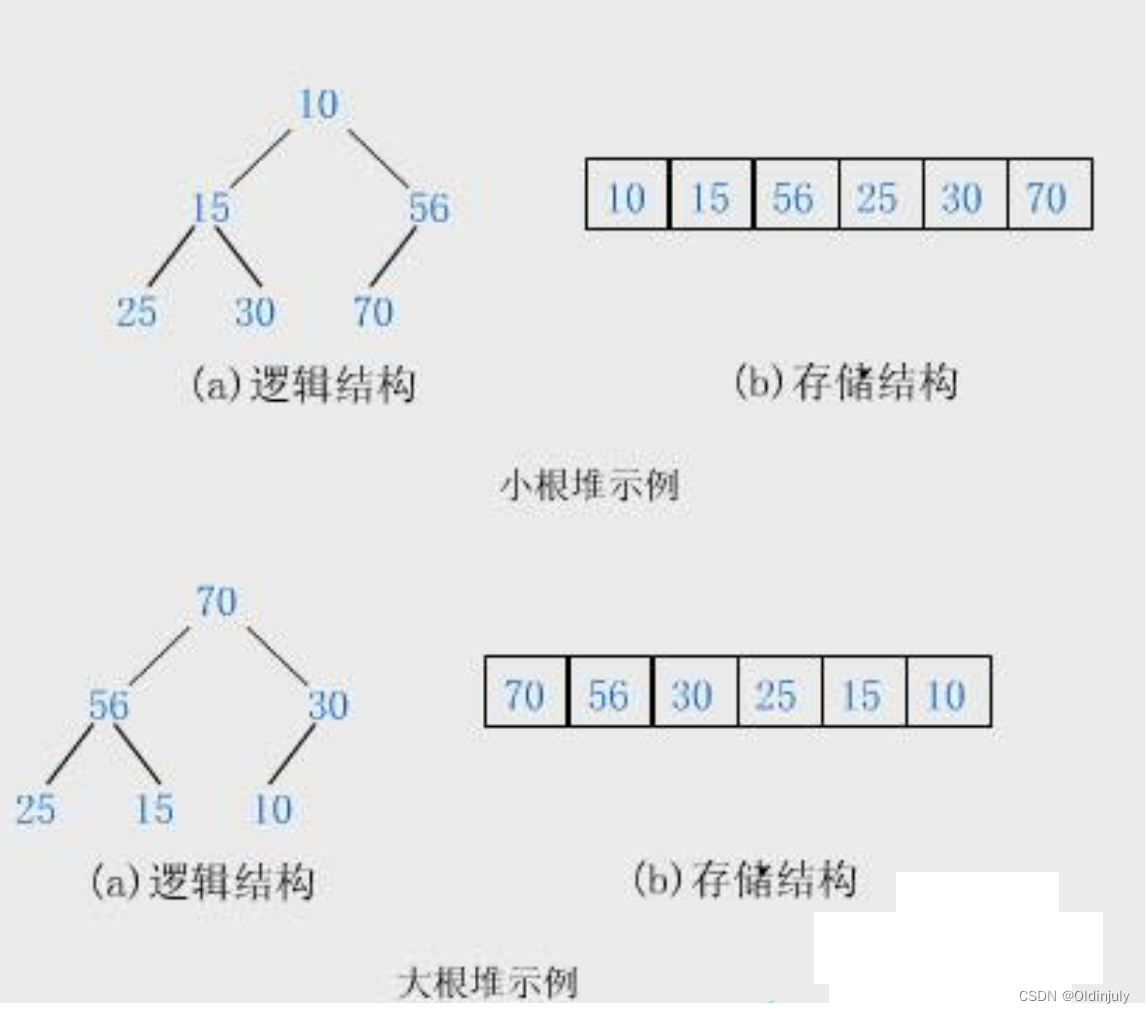
注意:所有的数组都可以表示成完全二叉树,但是他并不一定是堆。
3.堆的相关接口实现
补充:
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
1.若i>0,i位置节点的双亲序号:(i-1)/2; i=0,i为根节点编号,无双亲节点
2.若2i+1 < n,左孩子序号:2i+1;若2i+1>=n(数组越界), 无左孩子
(叶子就是没有左孩子,也就是叶子结点的左孩子下标2i+1>=n越界)
3.若2i+2 < n,右孩子序号:2i+2; 若2i+2>=n(数组越界), 无右孩子
3.1 堆的插入及向上调整算法
- 先将元素插入到堆的末尾,即最后一个数组元素之后
- 插入之后如果堆的性质遭到破坏,插入的结点就根据向上调整算法找到合适位置即可
3.1.1 向上调整算法
那么什么是向上调整算法呢?如何实现?
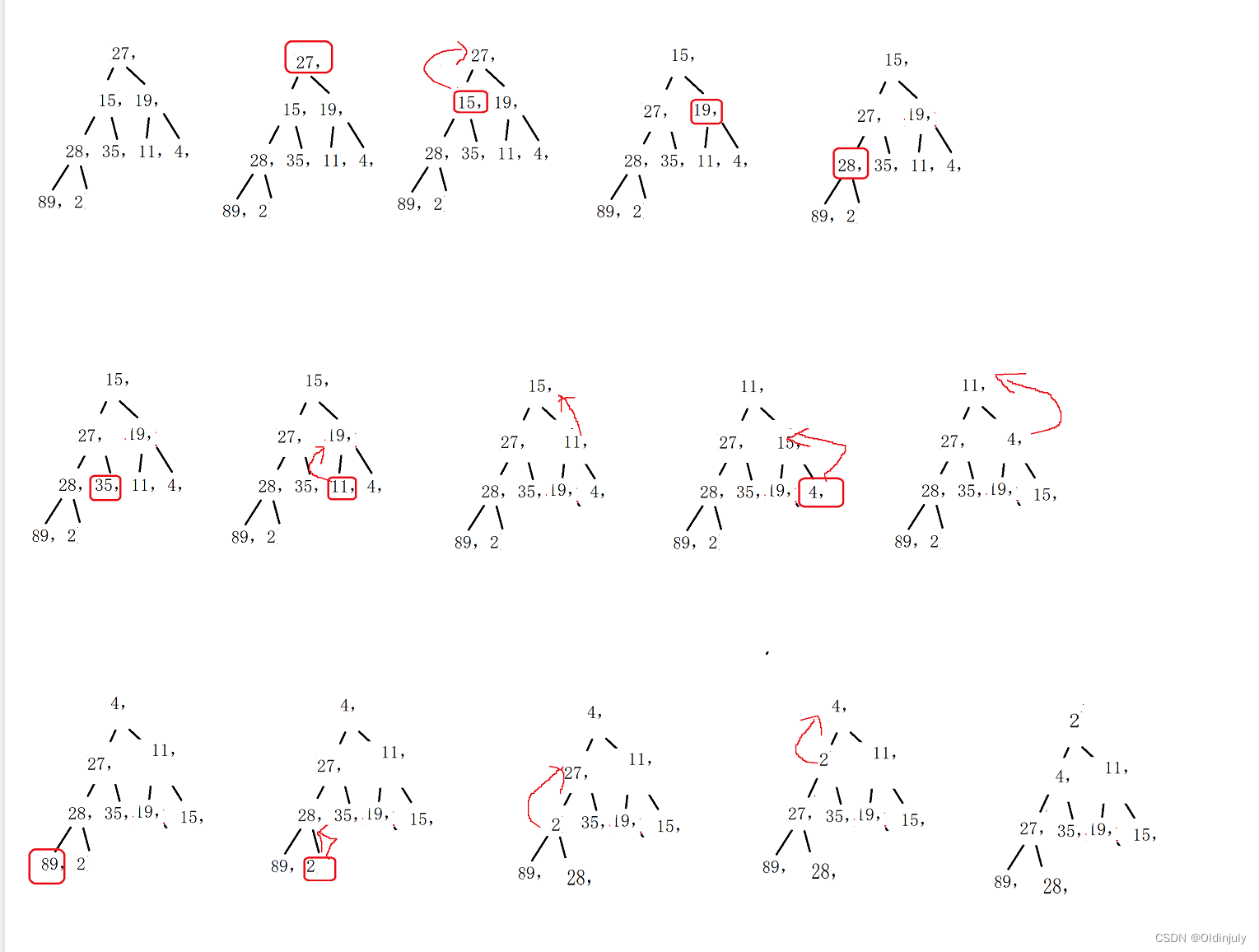
例如: 堆:[4, 27, 11, 28, 35, 19, 15, 89, 2] Push:2
图片展示:
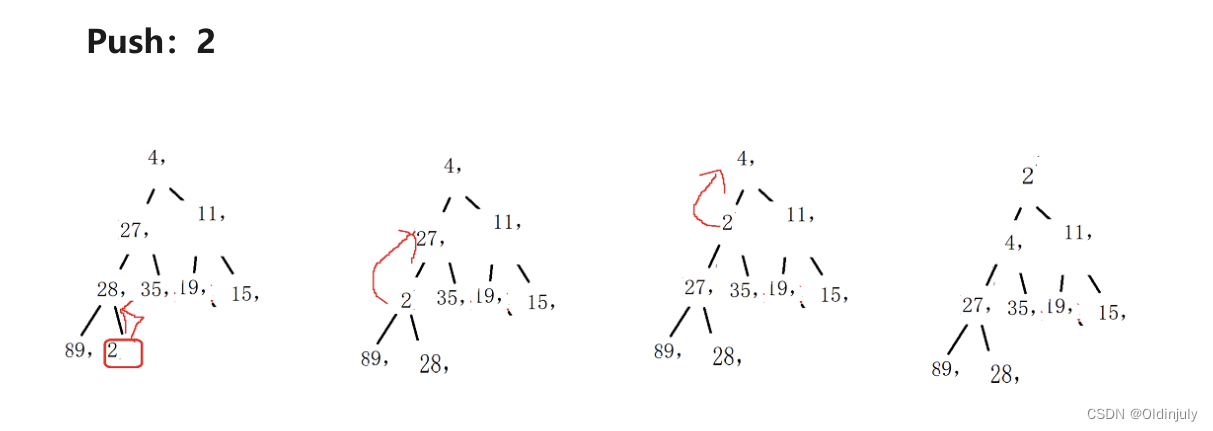
代码实现:
void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(a + child, a + parent);child = parent;parent = (parent - 1) / 2;}else{break;}}
}
代码注意事项:
- 除了插入的元素,堆中的其他元素都符合堆的性质,所以调整到 待调整节点和父节点 符合堆的性质即可退出调整。
- 循环退出条件:待调整节点调整到根节点 或者 待调整节点和父节点的大小关系符合堆的性质。
- while语句中的条件不能写parent >= 0,因为 (0-1)/ 2 之后依旧是0,并不符合预期的循环退出条件。
- 如果调大堆,比较符号就用>;如果调小堆,比较符号就用<;方便以后更改。
3.1.2 堆的插入
注意:堆的物理结构是一个数组,也就是用顺序表实现的,插入时容量不够要记得扩容。
void HeapPush(Heap* php, HPDataType x)
{assert(php);if (php->capacity == php->size){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (tmp == NULL){perror("HeapPush:");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}
3.2 堆的删除及向下调整算法
这里堆的删除是删除堆顶数据,因为只有堆顶数据才有意义(堆顶数据都是最值,删除堆顶后能获得次大或者次小的数)
这里我们能直接删除堆顶数据吗?很明显不可以,根据顺序表删除数据的特点,后面的元素会依次覆盖前面的元素,删除堆顶数据后,堆的结构就被破坏了。
其实删除思想是这样的:
- 将堆顶元素与堆中最后一个元素交换
- 删除堆中最后一个元素
- 将堆顶元素向下调整直到满足堆的结构
这种思想很巧妙,在后面的堆排序中也会用到这种思想。
3.2.1 向下调整算法
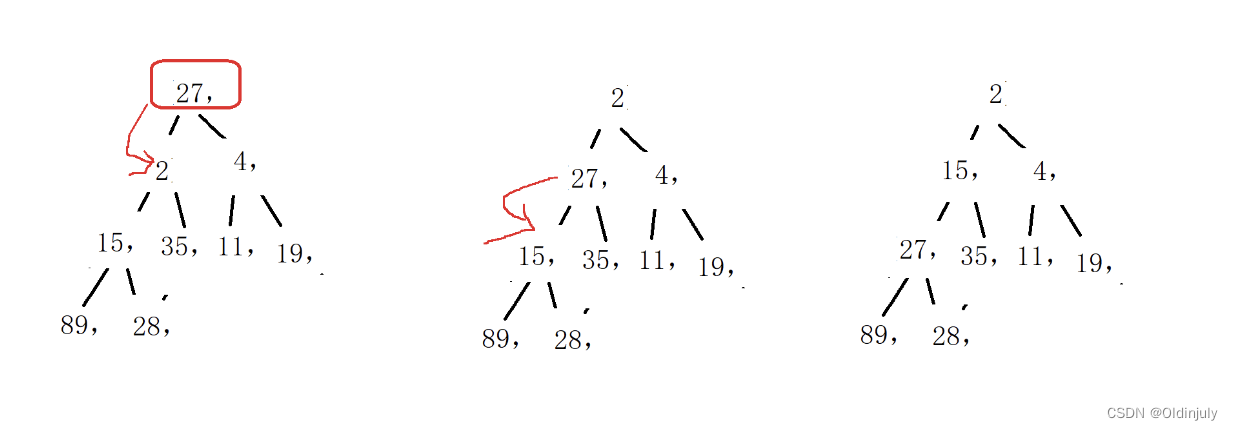
代码实现:
void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child + 1] > a[child])child++;if (a[child] > a[parent]){Swap(a + child, a + parent);parent = child;child = child * 2 + 1;}else{break;}}
}
代码注意事项:
- 除了堆顶元素,堆中的其他元素都符合堆的性质,所以调整到 待调整节点和左右孩子 符合堆的性质即可退出调整。
- 循环退出条件:待调整节点调整到叶子节点 或者 待调整节点和左右孩子节点的大小关系符合堆的性质。
- 因为要判断越界,函数参数中要有数组大小size。
- 向下调整时,我们要和该结点的左右孩子中较小的那个交换。代码设计时我们可以先默认左孩子小,再和右孩子进行比较得出较小的那个节点。
3.2.2 堆的删除
void HeapPop(Heap* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}
3.3 其它接口和代码实现
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <time.h>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}Heap;void Swap(int* a, int* b);
void AdjustUp(int* a, int child);//a:要调整的孩子结点所在的数组 child:要调整的孩子节点的下标
void AdjustDown(int* a, int size, int parent);//a:要调整的父亲结点所在的数组 size:数组的size parent:要调整的父亲节点的下标void HeapPrint(Heap* php);
void HeapInit(Heap* php);
void HeapDestory(Heap* php);
void HeapPush(Heap* php, HPDataType x);
void HeapPop(Heap* php);
HPDataType HeapTop(Heap* php);
int HeapSize(Heap* php);
int HeapEmpty(Heap* php);
#include "Heap.h"void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//调da堆
void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(a + child, a + parent);child = parent;parent = (parent - 1) / 2;}else{break;}}
}//调da堆
void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child + 1] > a[child])child++;if (a[child] > a[parent]){Swap(a + child, a + parent);parent = child;child = child * 2 + 1;}else{break;}}
}void HeapInit(Heap* php)
{assert(php);php->a = NULL;php->capacity = php->size = 0;
}void HeapDestory(Heap* php)
{free(php->a);php->capacity = php->size = 0;
}void HeapPrint(Heap* php)
{for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}void HeapPush(Heap* php, HPDataType x)
{assert(php);if (php->capacity == php->size){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (tmp == NULL){perror("HeapPush:");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}//这里删除的是堆顶数据,只有堆顶数据才有意义
//1.swap(堆顶数据,最后一个数据)
//2.删除最后一个数据
//3.堆顶数据AdjustDown
void HeapPop(Heap* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}HPDataType HeapTop(Heap* php)
{assert(php);assert(php->size > 0);return php->a[0];
}int HeapSize(Heap* php)
{assert(php);return php->size;
}int HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}
4.建堆或数组调堆的两种方式及复杂度分析
前面我们说过,所有的数组都可以表示成完全二叉树,但是他并不一定是堆。那么我们如何将这个数组调整成堆呢?
我们首先会想到:把数组的值依次push到堆中,再把堆中数据依次赋值给数组,这样就把数组调整成了堆。但是实际应用中我们不会再写一个堆这样的数据结构,其次这种方式会有空间复杂度的消耗,所以我们不提倡这么做。
调堆方式有两种:向上调整建堆和向下调整建堆
4.1 向上调整建堆
4.1.1 建堆步骤
参考堆插入的思想,数组中的每个元素都可以看做新插入的节点。
从根结点开始调整,一直调整到最后一个结点。
想要调成成小堆:如果该结点小于父节点,就一直向上交换,直到不小于其父节点或者调整到根结点。
4.1.2 代码实现
int main()
{int a[] = { 27,15,19,28,35,11,4,89,2 };int size = sizeof(a) / sizeof(a[0]);//这里我们建小堆//方法一:向上调整算法for (int i = 0; i < size; i++)//从根结点开始调整,一直调整到最后一个结点。{AdjustUp(a, i);}for (int i = 0; i < size; i++){printf("%d ",a[i]);}return 0;
}
4.1.3 时间复杂度分析 --- O(N*logN)
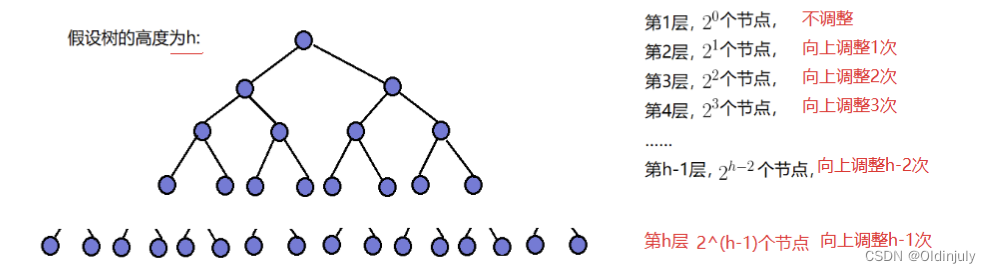
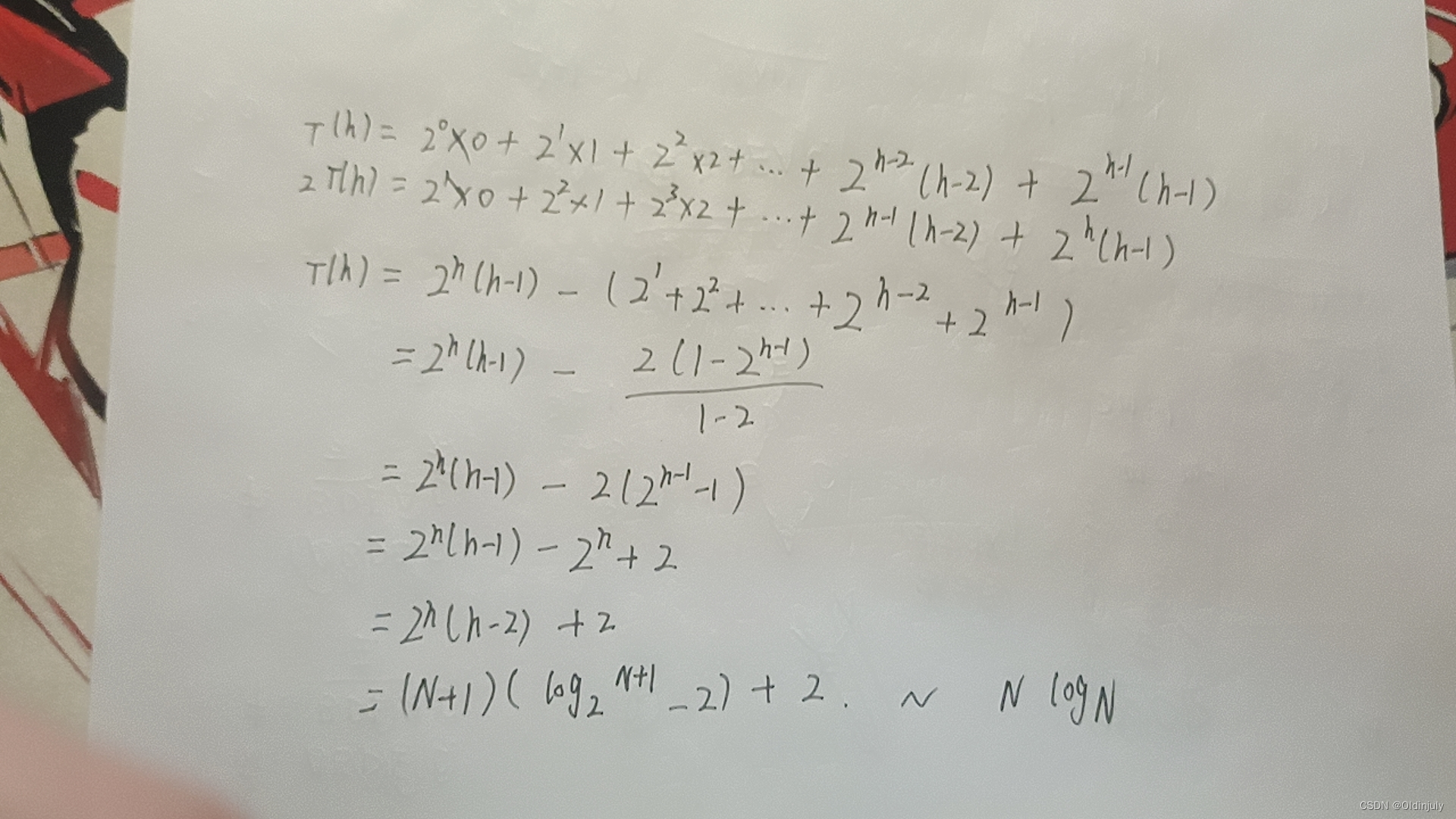
4.2 向下调整建堆
4.2.1 建堆步骤
在解释向下调整算法之前,先说明一下:
向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
那么我们如何调整呢?
这里我们可以利用递归思想来解决:先从倒数第一个非叶子结点的子树开始调整,一直调整到根结点的树。也就是倒着调整。
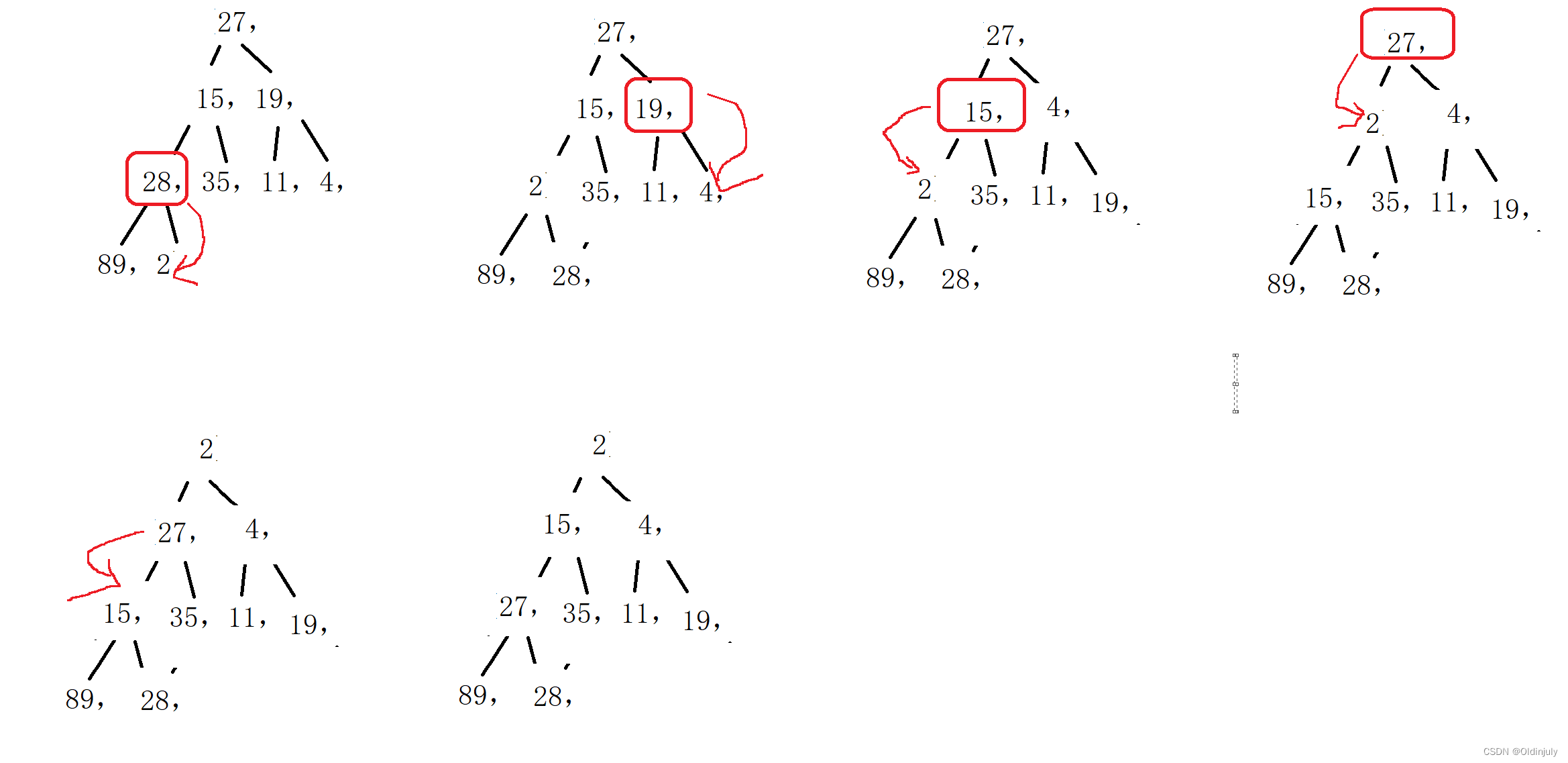
4.2.2 代码实现
int main()
{int a[] = { 27,15,19,28,35,11,4,89,2 };int size = sizeof(a) / sizeof(a[0]);//这里我们建小堆//方法二:向下调整算法for (int i = (size - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, size, i);}for (int i = 0; i < size; i++){printf("%d ",a[i]);}return 0;
}
代码注意:
size - 1是最后一个数组元素的下标,对他减1除2后,就是他父节点的下标,也就是倒数第一个非叶子结点;
4.2.3 时间复杂度分析 --- O(N)
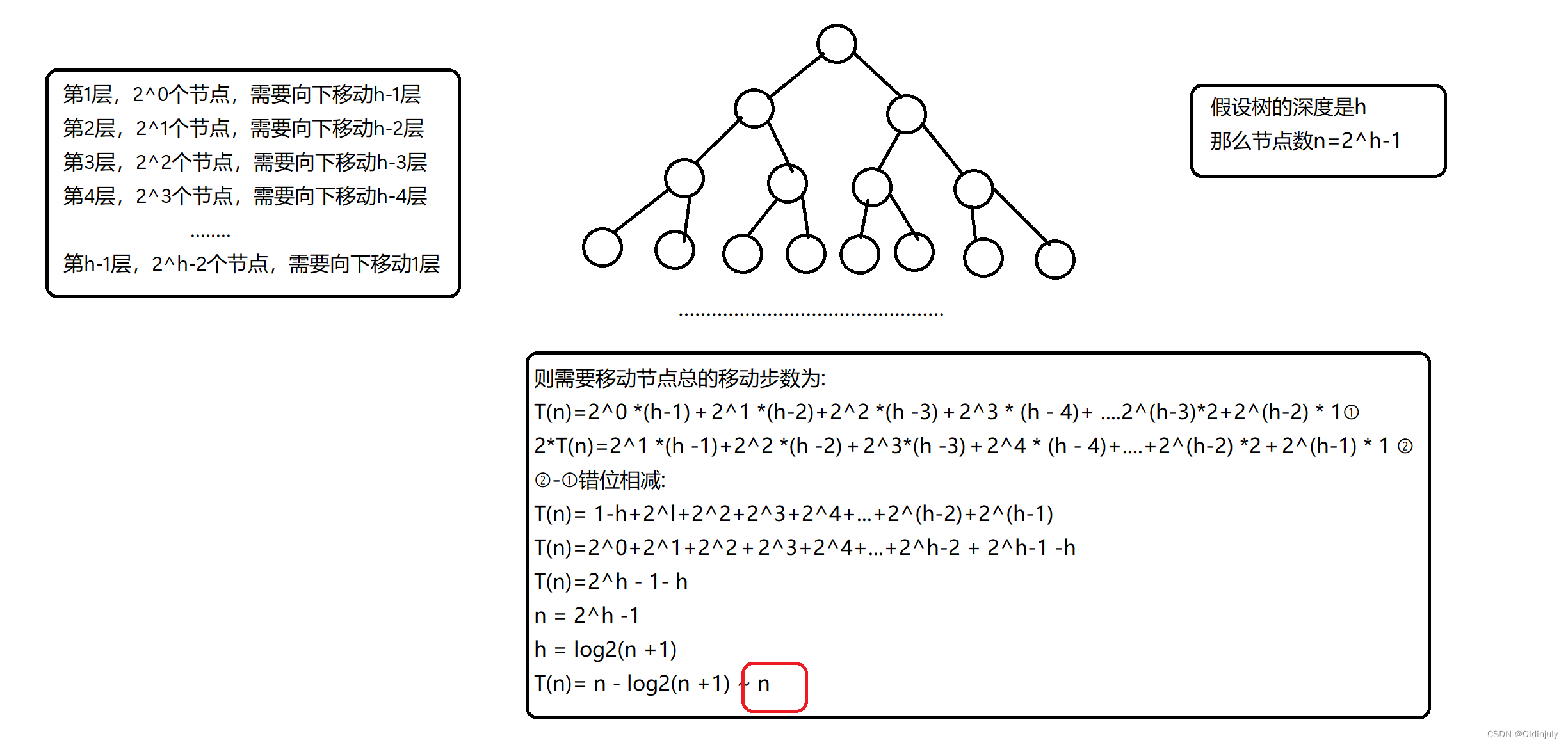
总结:向下调整算法建堆要比向上调整算法建堆要高效一些,并且向下调整算法要更常用(通常对堆顶数据进行向下调整操作),所以我们一般使用向下调整来建堆。
5.堆的应用
那么我们为什么要学堆呢?为什么要设计堆这种数据结构呢?
主要用于解决两个问题:
- 排序
- Topk问题:在N个数据中找最大或者最小的前k个(这里的N一般非常大)
注意:这里堆的应用问题和前面数组调堆的问题是同一个道理,我们不能使用堆数据结构的相关接口,需要在原生数组上进行操作。
5.1 堆排序(假设升序)
5.1.1 堆排序步骤
首先建堆这里就有一个坑了,正常思维来看,我们升序是建小堆,因为小堆的堆顶是最小值。
我们来看看升序建小堆的效率如何:
- 选出最小的数,放在第一个位置
- 最小的数删除后,剩下的看做一个堆。但是之前建好的关系都乱了,只能重新建堆,才能选出次小的数。
此时的时间复杂度:建堆的时间复杂度O(n),建了n次堆,时间复杂度O(n*n),这种效率还不如暴力遍历排序来的直接。
这里花里胡哨的建堆选堆顶的最值进行排序,结果效率和冒泡差不多,显然不是我们想要的结果。
那么堆排序到底是怎么排的呢,下面给出步骤
1.建堆
升序:建大堆
降序:建小堆
2.利用堆删除思想进行排序
(1)升序建的大堆,堆顶是最大元素,
(2)把堆顶(最大元素)和最后一个元素交换,
(3)最后一个元素(最大值)不看做堆中元素,堆顶元素向下调整,堆顶元素就变成了次大值,
(4)依次类推,重复(2)~(3)
可以计算一下这里的时间复杂度来和上面的建小堆方法来比较一下:
建大堆:n次向下调整,每次调整时间复杂度为O(logn),所以时间复杂度为:O(n*logn)
建小堆的时间复杂度O(n*n),很显然,数据非常多时,这两种方法的效率是天差地别
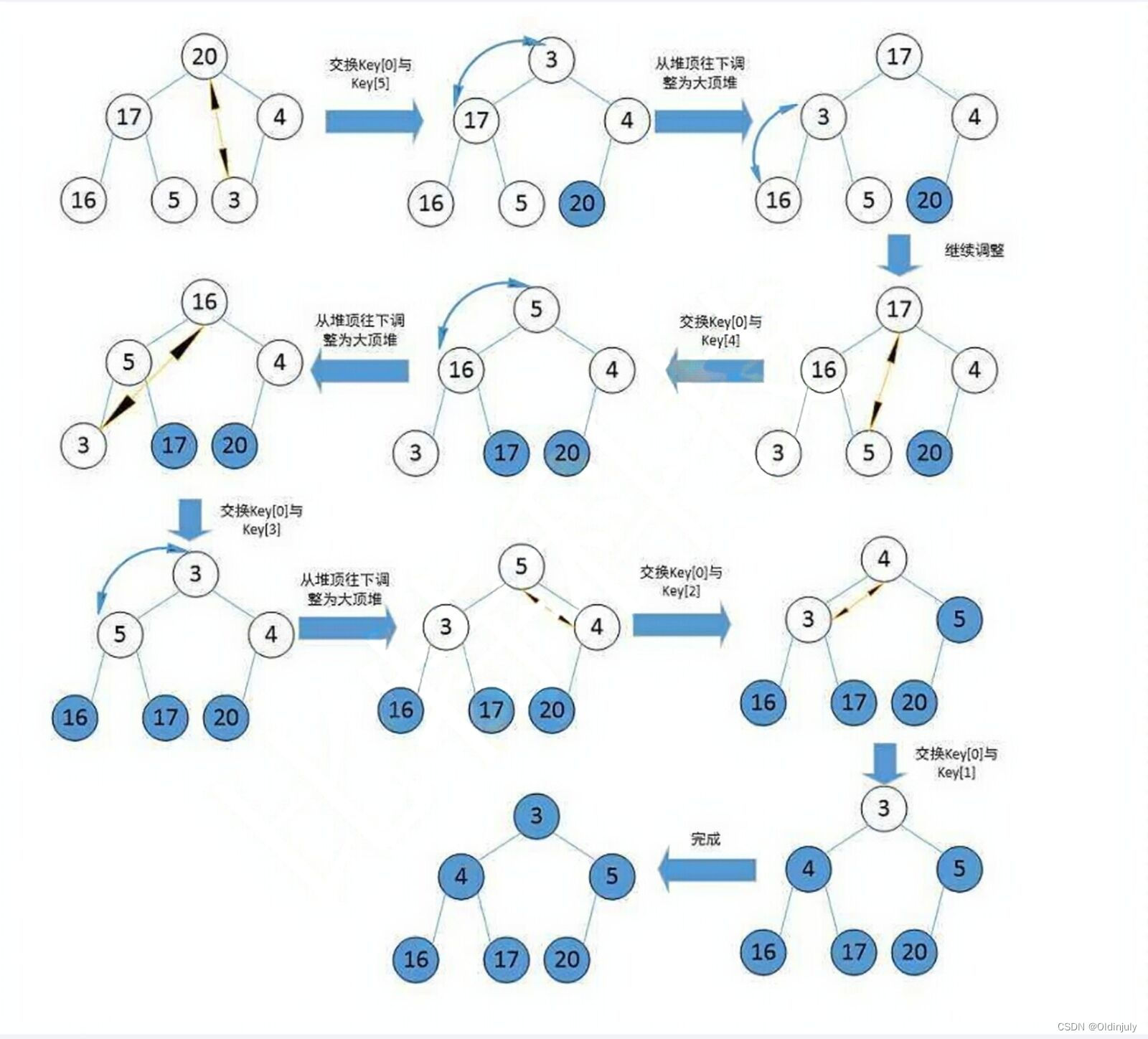
5.1.2 代码实现
//堆排序,升序
void HeapSort(int* a, int n)
{//第一步:建大堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}//第二步:堆删除思想进行排序(依次选数,调堆)for (int i = n - 1; i > 0; i--)//最后一步交换后就一个堆顶元素(最小值),AdjustDown没有进行调整{//将堆顶元素和最后一个元素交换,交换后最后一个元素不计入堆内Swap(&a[0], &a[i]);AdjustDown(a, i , 0);//这里第二个参数是数据个数,最后一个元素不计入堆内,正好是i}
}
代码注意事项:
- 以后我们建堆都用向下调整建堆。首先高效,其次堆排序的选数调堆也用的向下调整。
- 这里的循环变量i是最后一个元素的下标,也正好是交换后数组的元素个数(交换后最后一个元素不计入数组内)
- 最后一步i == 1时,交换后就一个堆顶元素(最小值),AdjustDown没有进行调整,但这一步也要执行,因为a[0]和a[1]要进行交换。
5.2 TopK问题
5.2.1 TopK解决步骤
Topk问题就是在N个数中找最大或者最小的前k个。(这里的N一般非常大,大到内存装不下)
第一次碰到这个问题,我们的惯性思维会去怎么解决呢?
- 方法一:先排降序,前k个最大
- 方法二:N个数依次插入大堆,pop k次,每次取的都是堆顶数据
但是当N非常大时,甚至内存都放不下,很显然这两种方法不靠谱。
我们可以算一下时间复杂度:
方法一:O(N*logN)
方法二:O(N+klogN) 建堆:N,k次pop :klogN
我们直接来说说Topk问题的实际解决办法:
- 用数据集合的前k个元素来建堆
前k个最大的元素:建小堆
前k个最小的元素:建大堆
2.用剩余的N-k个元素依次与对顶元素比较,找最大(小)的k个:比堆顶大(小),替换,向下调整。
3.最后堆中的k个元素就是最大(最小)的k个数
计算时间复杂度:O(k+(N-k)logk)~O(Nlogk)
5.2.2 代码实现(数据从文件读取)
int* TopK(int k)
{int* retArr = (int*)malloc(sizeof(int) * k);//打开文件FILE* pf = fopen("data,txt", "r");if (pf == NULL) {perror("TopK:");exit(-1); }//前k个数据读入数组for (int i = 0; i < k; i++){fscanf(pf, "%d", &retArr[i]);}//数组建堆(小堆)for (int i = (k - 2) / 2; i >= 0; i--){AdjustDown(retArr, k, i);}//剩余N-k个数据,依次和堆顶数据比较for (int i = 0; i < N - k; i++) {int x;fscanf(pf, "%d", &x);if (x > retArr[0]){retArr[0] = x;AdjustDown(retArr, k, 0);}}fclose(pf);return retArr;
}void testTopK()
{int* arr = TopK(10);for (int i = 0; i < 10; i++)printf("%d ", arr[i]);printf("\n");free(arr);
}
相关文章:

二叉树顺序存储结构
目录 1.二叉树顺序存储结构 2.堆的概念及结构 3.堆的相关接口实现 3.1 堆的插入及向上调整算法 3.1.1 向上调整算法 3.1.2 堆的插入 3.2 堆的删除及向下调整算法 3.2.1 向下调整算法 3.2.2 堆的删除 3.3 其它接口和代码实现 4.建堆或数组调堆的两种方式及复杂度分析…...
Apache HTTPD 多后缀解析漏洞复现
Apache HTTPD 支持一个文件拥有多个后缀,并为不同后缀执行不同的指令。比如,如下配置文件: AddType text/html .html AddLanguage zh-CN .cn 其给.html后缀增加了media-type,值为text/html;给.cn后缀增加了语言&…...

【深入浅出C#】章节10: 最佳实践和性能优化:内存管理和资源释放
一、 内存管理基础 1.1 垃圾回收机制 垃圾回收概述 垃圾回收(Garbage Collection)是一种计算机科学和编程领域的重要概念,它主要用于自动管理计算机程序中的内存分配和释放。垃圾回收的目标是识别和回收不再被程序使用的内存,以…...

我的创作纪念日——1个普通网安人的漫谈
机缘 大家好,我是zangcc。今天突然收到了一条私信,才发现来csdn已经1024天了,不知不觉都搞安全渗透2年半多了🐔,真是光阴似箭。 我写博客的初衷只是记录自己的学习历程,比如打打靶场,写一下通关…...
Linux中执行bash脚本报错/bin/bash^M: bad interpreter: No such file or directory
文章目录 参考博客: Linux中执行bash脚本报错/bin/bash^M: bad interpreter: No such file or directory 首先在此对这位博主表示感谢。 运行bash脚本会出现两个文件,1037.err和1037.out。 1037.err的文件内容如下: /data/home/user12/.lsbat…...

期权交易策略主要有哪些?期权交易策略指南
在学习更复杂的看涨和看跌期权策略之前,普通投资者应该彻底了解一些关于期权的基本知识,这样有助你后期的交易能力和理论知识水平提升有很大的帮助,下文科普期权交易策略主要有哪些?期权交易策略指南!本文来自…...

算法通关村第十四关——解析堆在数组中找第K大的元素的应用
力扣215题, 给定整数数组nums和整数k,请返回数组中第k个最大的元素。 请注意,你需要找的是数组排序后的第k个最大的元素,而不是第k个不同的元素。 分析:按照“找最大用小堆,找最小用大堆,找中间…...
【报错】springboot3启动报错
报错内容:Cannot load driver class: org.h2.Driver Error starting ApplicationContext. To display the condition evaluation report re-run your application with debug enabled. 解决; 通过源码分析,druid-spring-boot-3-starter目前最新版本是1…...
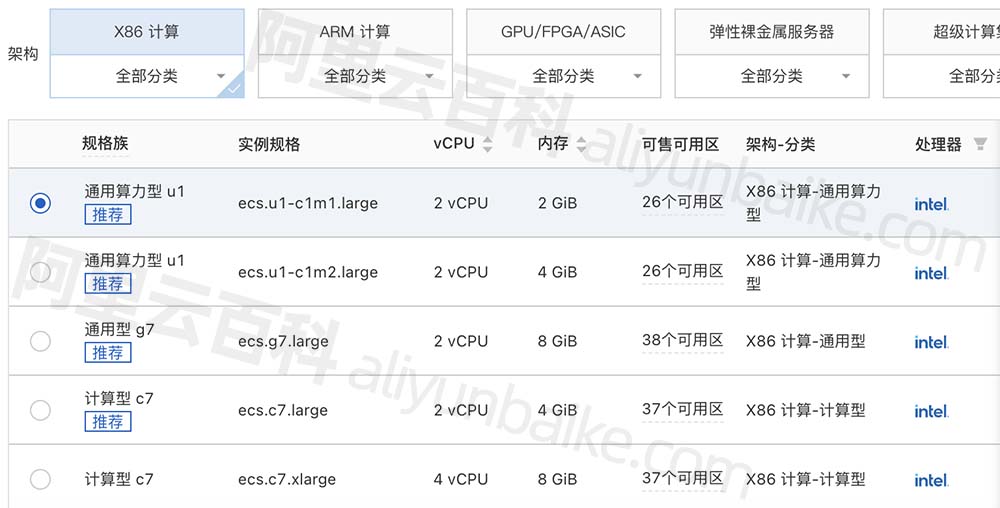
阿里云服务器配置怎么选择?小白攻略
阿里云服务器配置选择_CPU内存/带宽/存储配置_小白指南,阿里云服务器配置选择方法包括云服务器类型、CPU内存、操作系统、公网带宽、系统盘存储、网络带宽选择、安全配置、监控等,阿小云分享阿里云服务器配置选择方法,选择适合自己的云服务器…...
关于 RK3568的linux系统killed用户应用进程(用户现象为崩溃) 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/132710642 红胖子网络科技博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软硬…...
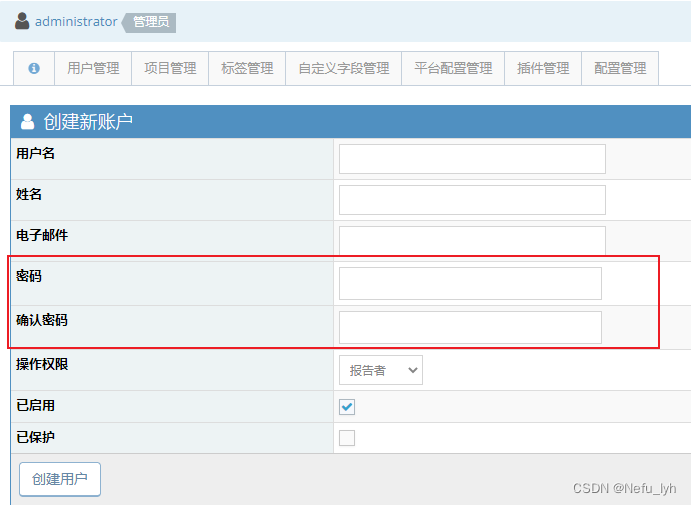
EasyPHP-Devserver-17安装和配置mantisBT
文章目录 1、准备工作2、安装easyphp2.1 http://127.0.0.1 无法访问 3、安装mantisBT和phpMyAdmin3.1 配置浏览器的访问url和端口号(配置局域网内可访问)3.2 安装mantis 4、Administrator 注册新用户时设置登录密码5、附件上传6、邮件配置 文章参考自&am…...

Python打包教程 PyInstaller和cx_Freeze
当我们开发Python应用程序时,通常会将代码保存在.py文件中,然后通过Python解释器运行它。这对于开发和测试是非常方便的,但在将应用程序分享给其他人或在不同环境中部署时,可能会带来一些问题。为了解决这些问题,我们可…...
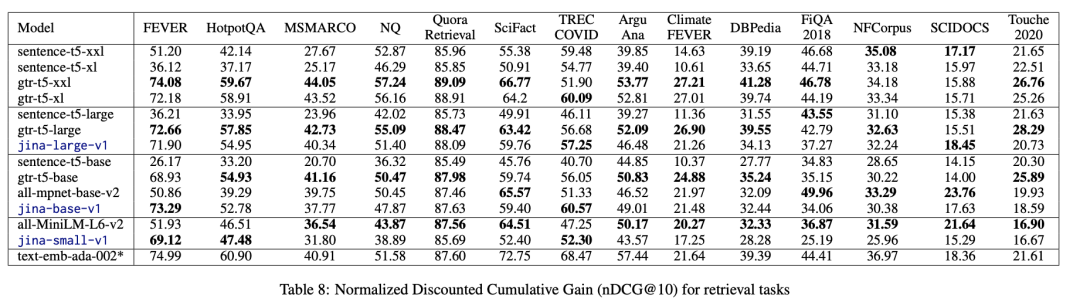
用两成数据也能训练出十成功力的模型,Jina Embeddings 这么做
句向量(Sentence Embeddings)模型在多模态人工智能领域起着至关重要的作用,它通过将句子编码为固定长度的向量表示,将语义信息转化为机器可以处理的形式,在 文本分类、信息检索和相似度计算 等多个方面有着广泛应用。 …...
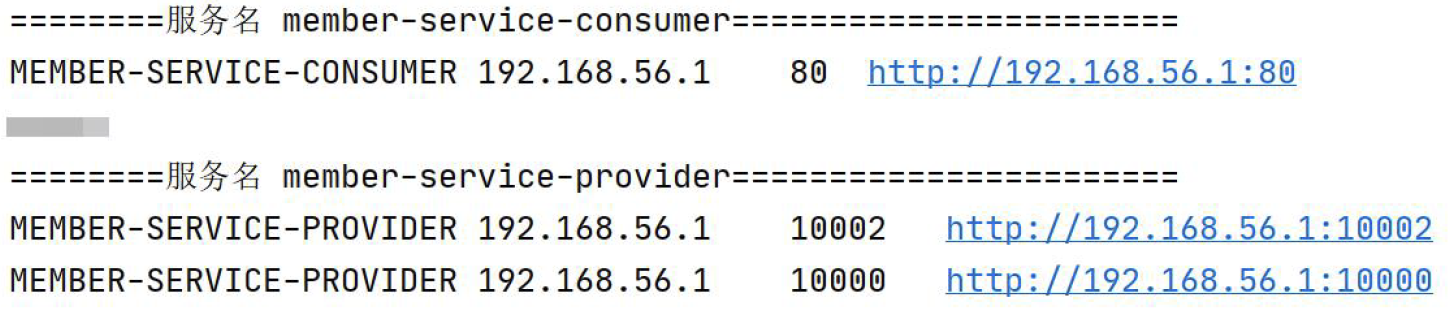
SpringCloud Eureka搭建会员中心服务提供方-集群
😀前言 本篇博文是关于SpringCloud Eureka搭建会员中心服务提供方-集群,希望你能够喜欢 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章可以帮助到大家,您…...
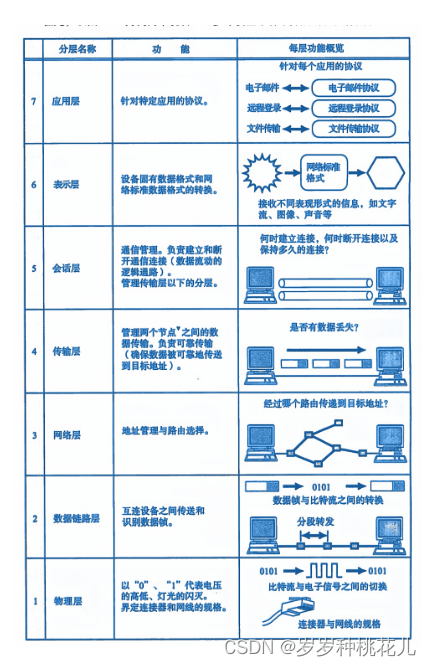
详解TCP/IP协议第二篇:OSI参考模型详解
文章目录 写给自己的话 一:协议分层与OSI参考模型 二:通过对话理解分层 三:OSI参考模型 写给自己的话 不从恶人的计谋,不站罪人的道路,不坐亵慢人的座位,惟喜爱耶和华的律法,昼夜思想&#…...

OpenGL 函数列表
//纹理头文件加载 #define STB_IMAGE_IMPLEMENTATION #include "stb_image.h" //线框模式(Wireframe Mode) //glPolygonMode(GL_FRONT_AND_BACK, GL_LINE); //翻转y轴 stbi_set_flip_vertically_on_load(true); //声明鼠标滚轮回调函数 void scroll_call…...

【C语言】每日一题(半月斩)——day1
目录 😊前言 一.选择题 1.执行下面程序,正确的输出是(c) 2.以下不正确的定义语句是( ) 3.test.c 文件中包括如下语句,文件中定义的四个变量中,是指针类型的变量为【多选】&a…...

Spring MVC 七 - Locale 本地化
Spring各模块都支持国际化,SpringMVC也同样支持。DispatcherServlet通过Locale Resovler自动根据客户端的Locale支持国际化。 request请求上来后,DispatcherServlet查找并设置Locale Resovler,我们可以通过RequestContext.getLocale()获取到…...
算法_C++——替换后的最长重复字符)
力扣(LeetCode)算法_C++——替换后的最长重复字符
给你一个字符串 s 和一个整数 k 。你可以选择字符串中的任一字符,并将其更改为任何其他大写英文字符。该操作最多可执行 k 次。 在执行上述操作后,返回包含相同字母的最长子字符串的长度。 示例 1: 输入:s “ABAB”, k 2 输出…...

unity 编辑器时读取FairyGUI图集单个图像
原因 想要在编辑器扩展也能访问FairyGUI图集里面的小图,随便找了一下没有找到接口自己做一个 方法 使用UIPackage.GetItemByURL获得小图信息。从图集中复制出小图,如果有旋转就逆旋转90度即可 图集里面的小图是有可能旋转的,可以通过访问 …...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

