OpenCV之霍夫变换检测直线
霍夫变换
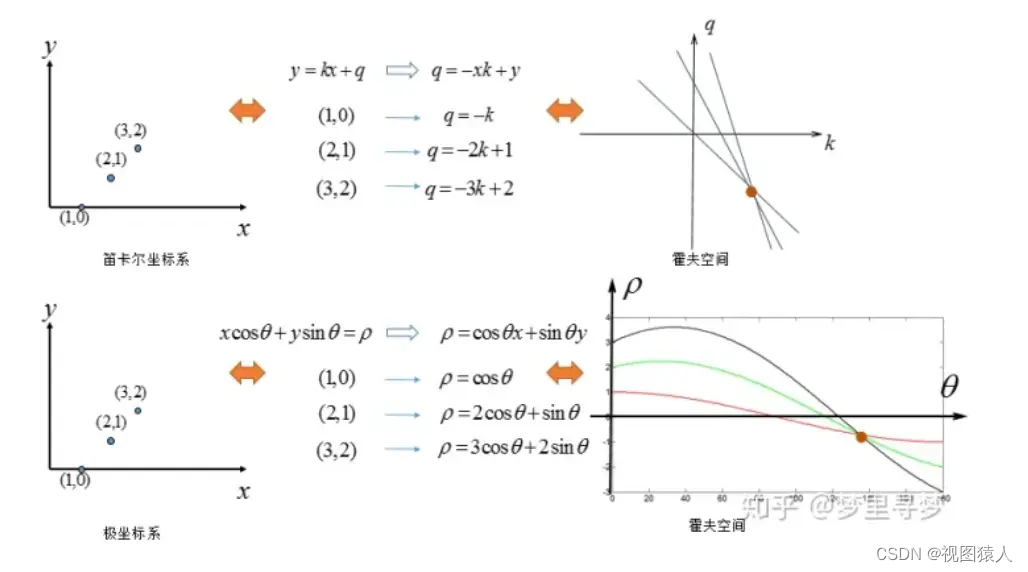
首先是笛卡尔坐标系到霍夫空间的转换,比如笛卡尔坐标系中有一条直线 y=ax+b。
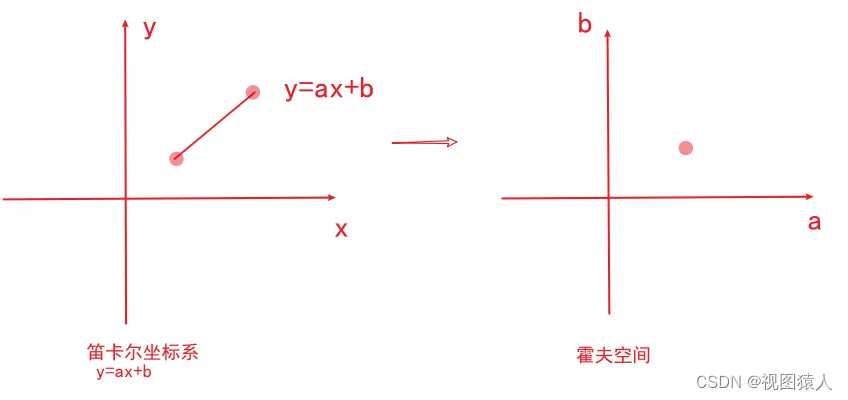
笛卡尔坐标系中一条直线,对应霍夫空间的一个点。
反过来同样成立(霍夫空间的一条直线,对应笛卡尔坐标系的一个点)
原理其实很简单
比如
(1)笛卡尔坐标系内y=ax+b 一条直线确定时 它的斜率和截距是确定的 即是a b是确定的,因此到了霍夫空间内就对应一个(a,b) 即是笛卡尔中一条直线对应霍夫空间一个点
(2)笛卡尔坐标系内一个点 比如x1,y1 相当于x1 y1是确定的 在霍夫空间中
b=-xa+y 即是 b=-x1a+y1 代表的是一条直线 即是笛卡尔中一个点对应霍夫空间一条直线
(3)笛卡尔坐标系多个点
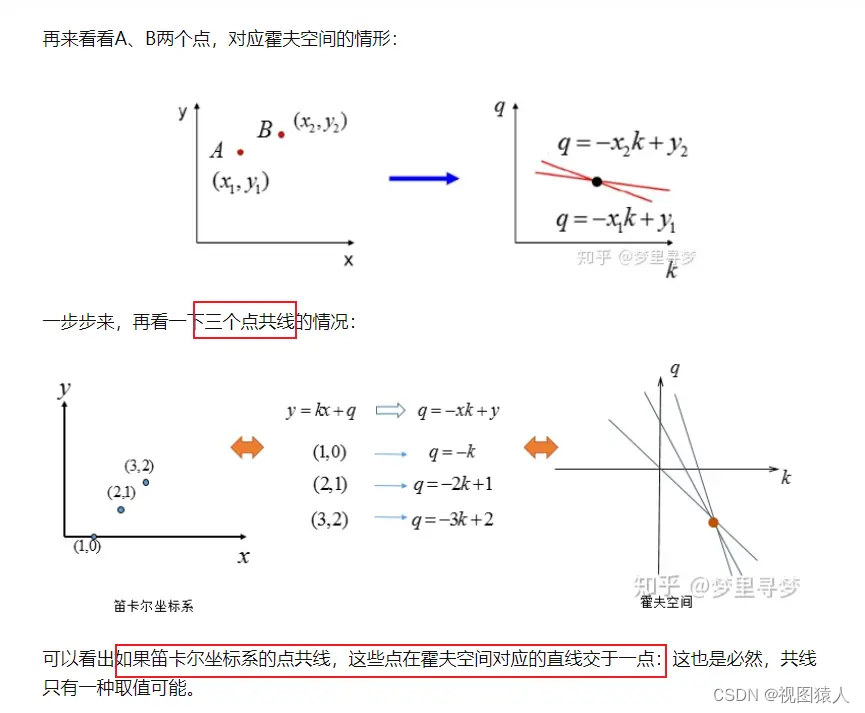
这些点如果共线 就相当于回到了(1) 笛卡尔坐标系中一条直线对应霍夫空间一个点
(4)笛卡尔坐标系多个点 不共线
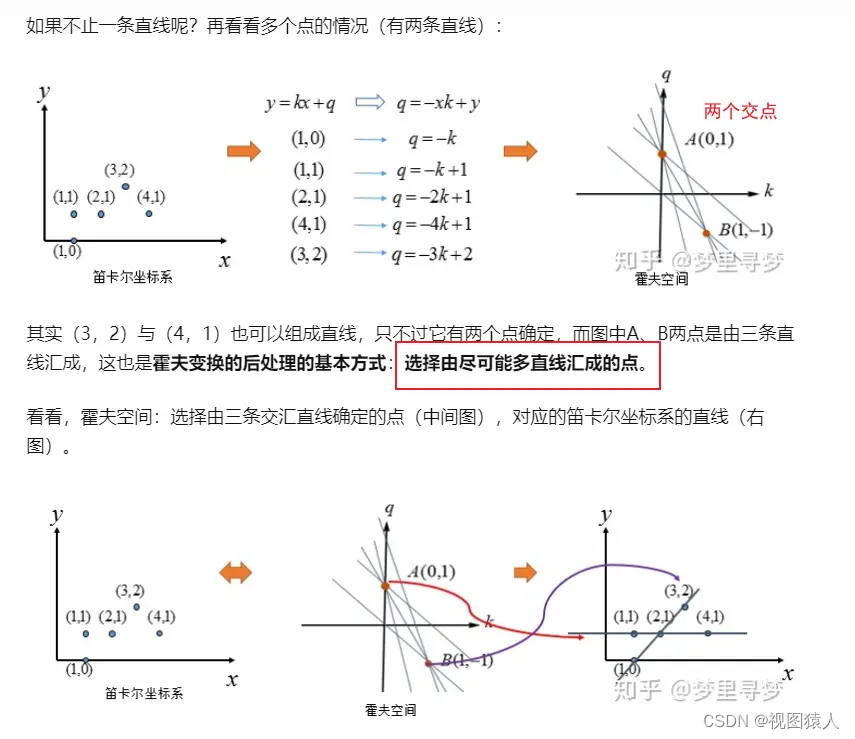
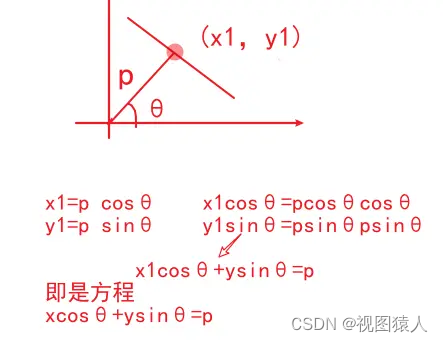
(5)但是 如果直线斜率不存在的时候 霍夫空间那就不容易表示
因此我们换成极坐标 一样的转换原理
先求极坐标方程 其中参数从斜率a和截距b变成 极径p和极角θ
比如下面的变换对比
具体计算过程举例:

OpenCV C++实现
/*
*参数说明:
*src:待检测的原图像
*rho:以像素为单位的距离分辨率,即距离r离散时的单位长度
*theat:以角度为单位的距离分辨率,即角度Θ离散时的单位长度(取值的步长)
*Threshold:累加器阈值,参数空间中离散化后每个方格被通过的累计次数大于该阈值,则该方格代表的直线被视为在原图像中存在
*lines:检测到的直线极坐标描述的系数数组,每条直线由两个参数表示,分别为直线到原点的距离r和原点到直线的垂线与x轴的夹角
*/
void myHoughLines(Mat src, double rho, double theat, int Threshold, vector<Vec2f>& lines)
{if (src.empty() || rho < 0.1 || theat>360 || theat < 0)return;int row = src.rows;int col = src.cols;Mat gray;if (src.channels() > 1){cvtColor(src, gray, COLOR_BGR2GRAY);}elsesrc.copyTo(gray);int maxDistance = sqrt(src.cols * src.cols + src.rows * src.rows); // 图像任意两点最大距离int houghMat_cols = 360 / theat; // theat是角度取值的步长 霍夫变换后距离夹角坐标下对应的Mat的宽(一共多少个θ)int houghMat_rows = maxDistance / rho; // 霍夫坐标距离夹角下对应的Mat的高 就是p的取值个数 Mat houghMat = Mat::zeros(houghMat_rows, houghMat_cols, CV_32FC1); // 存储p和 θ的矩阵//边缘检测Canny(gray, gray, 100, 200, 3);//二值化threshold(gray, gray, 160, 255, THRESH_BINARY);//遍历二值化后的图像for (int i = 0; i < row; i++){for (int j = 0; j < col; j++){if (gray.ptr<uchar>(i)[j] != 0){/*从0到360度遍历角度,得到一组关于距离夹角的离散点,即得到一组关于经过当前点(i,j)按单位角度theat旋转得到的直线*/for (int k = 0; k < 360 / theat; k += theat){// k * CV_PI / 180 是极角 θ double r = i * sin(k * CV_PI / 180) + j * cos(k * CV_PI / 180);// 找哪个(θ,r) 最多 if (r >= 0){ // 直线到原点的距离必须大于0 获得在霍夫变换距离夹角坐标系下对应的Mat的行的下标int r_subscript = r / rho;// 经过该直线的点数加1houghMat.at<float>(r_subscript, k) = houghMat.at<float>(r_subscript, k) + 1;}}}}}/*现在 houghMat 矩阵里面的数值N 是经过这点的线个数(极坐标下)比如说 (行,列)对应 (p, θ) 对应的值就是 经过(p, θ)的线一共N条经过直线的点数N 大于阈值, 则视为在原图中存在该直线 就要这条直线了 */for (int i = 0; i < houghMat_rows; i++){for (int j = 0; j < houghMat_cols; j++){if (houghMat.ptr<float>(i)[j] > Threshold){// line保存直线到原点的距离和直线到坐标原点的垂线和x轴的夹角 求p和θVec2f line(i * rho, j * theat * CV_PI / 180);lines.push_back(line);}}}}相关文章:

OpenCV之霍夫变换检测直线
霍夫变换 首先是笛卡尔坐标系到霍夫空间的转换,比如笛卡尔坐标系中有一条直线 yaxb。 笛卡尔坐标系中一条直线,对应霍夫空间的一个点。 反过来同样成立(霍夫空间的一条直线,对应笛卡尔坐标系的一个点) 原理其实很简单 …...
lv3 嵌入式开发-11 Linux下GDB调试工具
目录 1 GDB简介 2 GDB基本命令 3 GDB调试程序 1 GDB简介 GDB是GNU开源组织发布的一个强大的Linux下的程序调试工具。 一般来说,GDB主要帮助你完成下面四个方面的功能: 1、启动你的程序,可以按照你的自定义的要求随心所欲的运行程序&#…...
Zabbix监控平台概念
1.概念 Zabbix是一款开源的、免费的、分布式监控平台支持web管理,WEB界面可以方便管理员使用可以监控硬件服务器CPU温度、风扇转速、操作系统CPU、EME、DISK、I/O、流量宽带、负载、端口、进程等Zabbix是C/S架构,Client客户端和Server端组成 2.Zabbix可…...
【javaSE】 枚举与枚举的使用
文章目录 🎄枚举的背景及定义⚾枚举特性总结: 🌲枚举的使用🚩switch语句🚩常用方法📌示例一📌示例二 🎍枚举优点缺点🌴枚举和反射🚩枚举是否可以通过反射&…...
NetSuite知识会汇编-管理员篇顾问篇2023
本月初,开学之际,我们发布了《NetSuite知识会汇编-用户篇 2023》,这次发布《NetSuite知识会汇编-管理员篇&顾问篇2023》。本篇挑选了近两年NetSuite知识会中的一些文章,涉及开发、权限、系统管理等较深的内容,共19…...

根号分治与多项式的巧妙结合:GYM-104386G
使用范围:序列上对于每种数的计数问题 考虑对每种数的出现次数进行根号分治 如果出现次数很少,直接平方暴力即可 如果很大考虑任意 ( i , j ) (i,j) (i,j),我们拆一下,再移一下,然后就变成了卷积形式...

通过FTP高速下载几百G数据
基因组下载 (FTP) 常见问题解答 基因组FTP站点有哪些亮点?下载多个基因组组装数据的最简单方法是什么?下载大型数据集的最佳协议是什么?为什么 NCBI 基因组 FTP 站点要重组?我如何及时了解 NCBI 基因组 FTP 站点的变化?...

cudnn-windows-x86_64-8.6.0.163_cuda11-archive 下载
网址不太好访问的话,请从下面我提供的分享下载 Download cuDNN v8.6.0 (October 3rd, 2022), for CUDA 11.x 此资源适配 cuda11.x 将bin和include文件夹里的文件,分别复制到C盘安装CUDA目录的对应文件夹里 安装cuda时自动设置了 CUDA_PATH_V11_8 及path C:\Progra…...
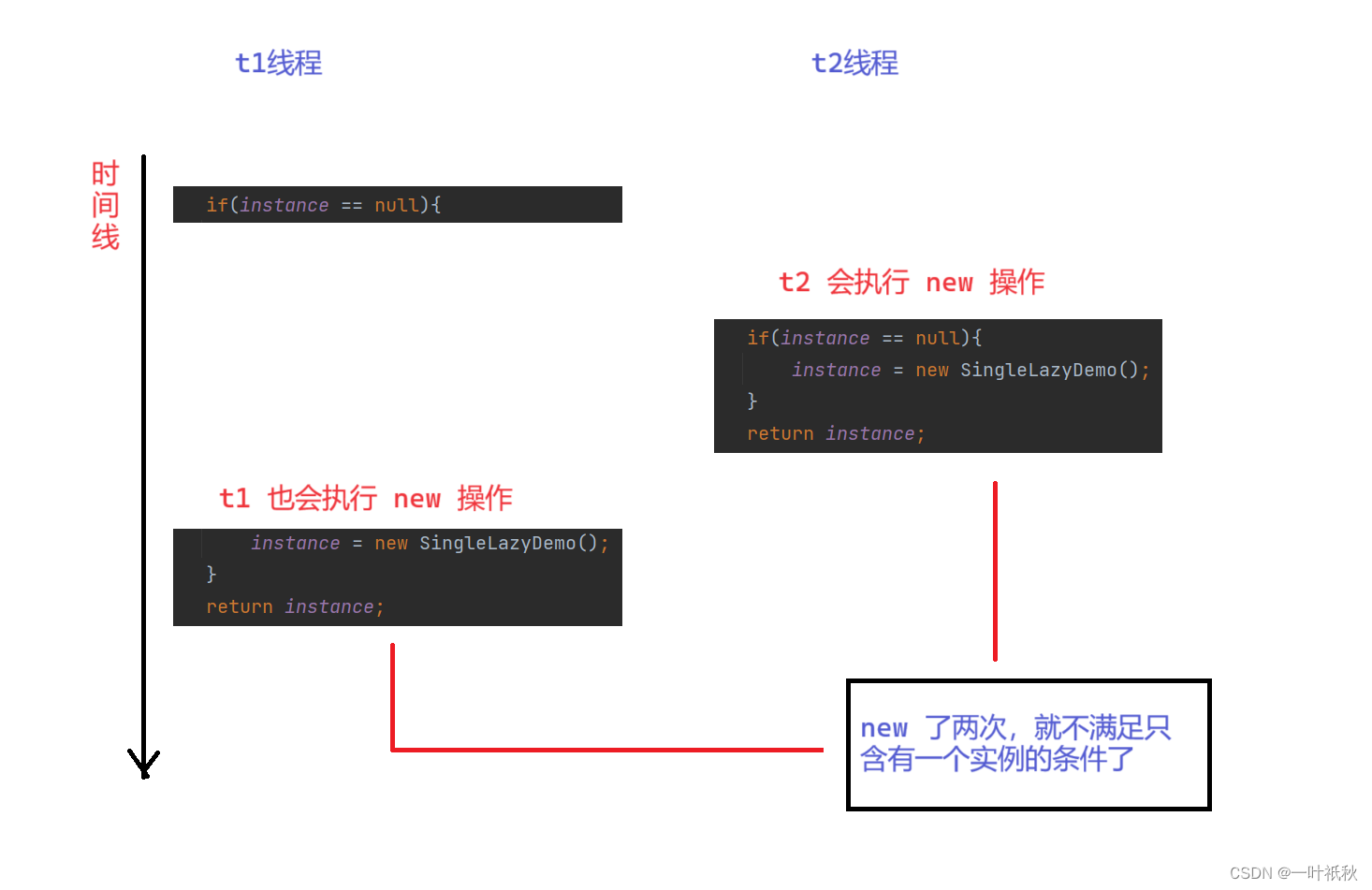
多线程案例(1) - 单例模式
目录 单例模式 饿汉模式 懒汉模式 前言 多线程中有许多非常经典的设计模式(这就类似于围棋的棋谱),这是用来解决我们在开发中遇到很多 "经典场景",简单来说,设计模式就是一份模板,可以套用。…...
)
Arduino驱动TCS34725传感器(颜色传感器篇)
目录 1、传感器特性 2、硬件原理图 3、控制器和传感器连线图 4、驱动程序 TCS34725是一款低成本,高性价比的RGB全彩颜色识别传感器,传感器通过光学感应来识别物体的表面颜色。...
知识库网站如何搭建?需要注意这五个要点!
正因为知识库提供结构化知识库来记载信息和知识,便于团队沉淀经验、共享资源,形成完整的知识体系并持续进化,使得它成为当前企业发展新宠。 构建自己/团队的知识库是一个良好的习惯,可以提高工作和学习效率,以下是一…...

【UE虚幻引擎】UE源码版编译、Andorid配置、打包
首先是要下载源码版的UE,我这里下载的是5.2.1 首先要安装Git 在你准备放代码的文件夹下右键点击Git Bash Here 然后可以直接git clone https://github.com/EpicGames/UnrealEngine 不行的话可以直接去官方的Github上下载Zip压缩包后解压 运行里面的Setup.bat&a…...
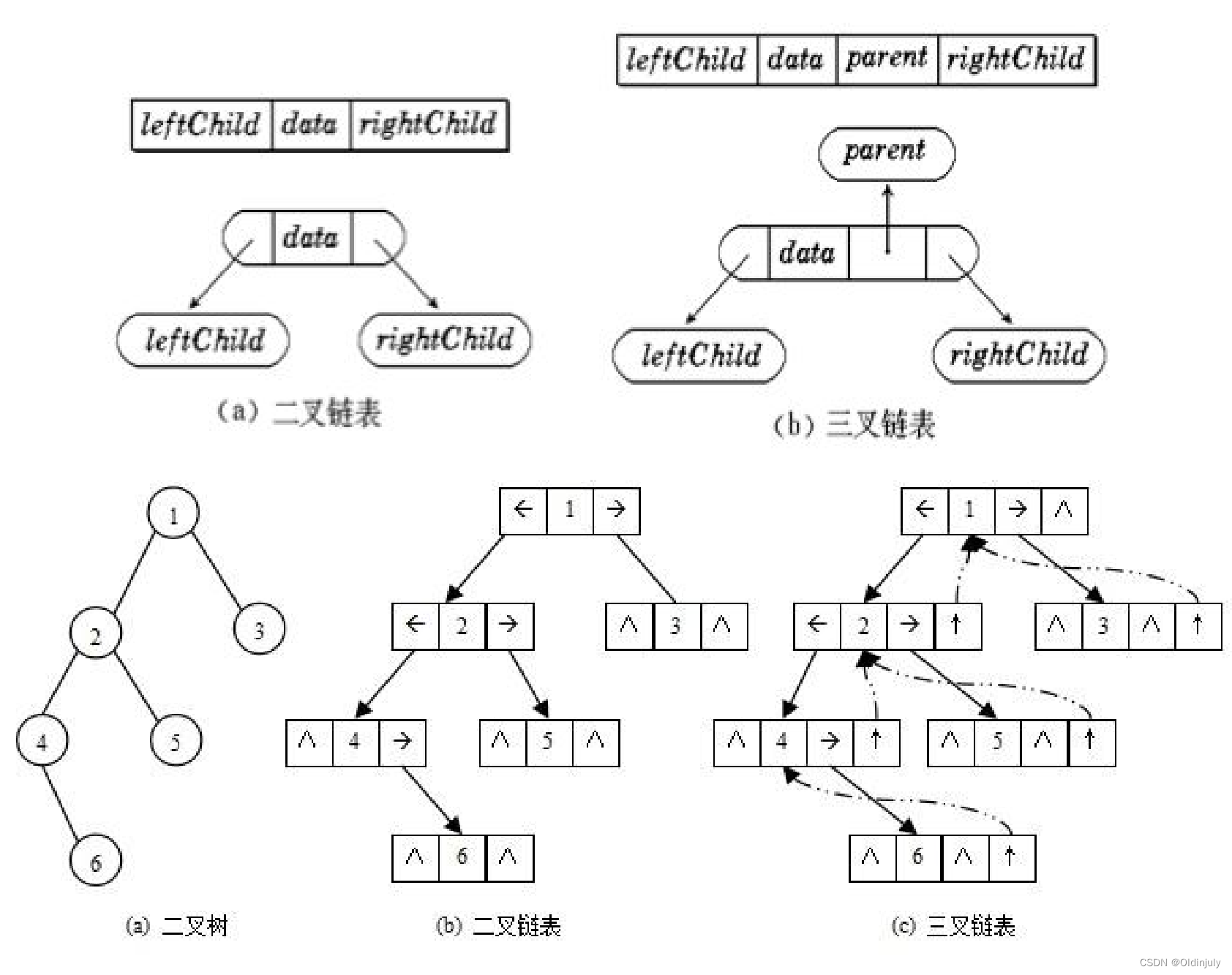
树和二叉树的相关概念及结构
目录 1.树的概念及结构 1.1 树的概念 1.2 树的相关概念 1.3 树的表示 1.3.1 孩子兄弟表示法 1.3.2 双亲表示法 1.4 树的实际应用 2.二叉树的概念及结构 2.1 二叉树的概念 2.2 特殊的二叉树 2.3 二叉树的性质 2.4 二叉树的存储 2.4.1 顺序存储 2.4.2 链式存储 1.树…...
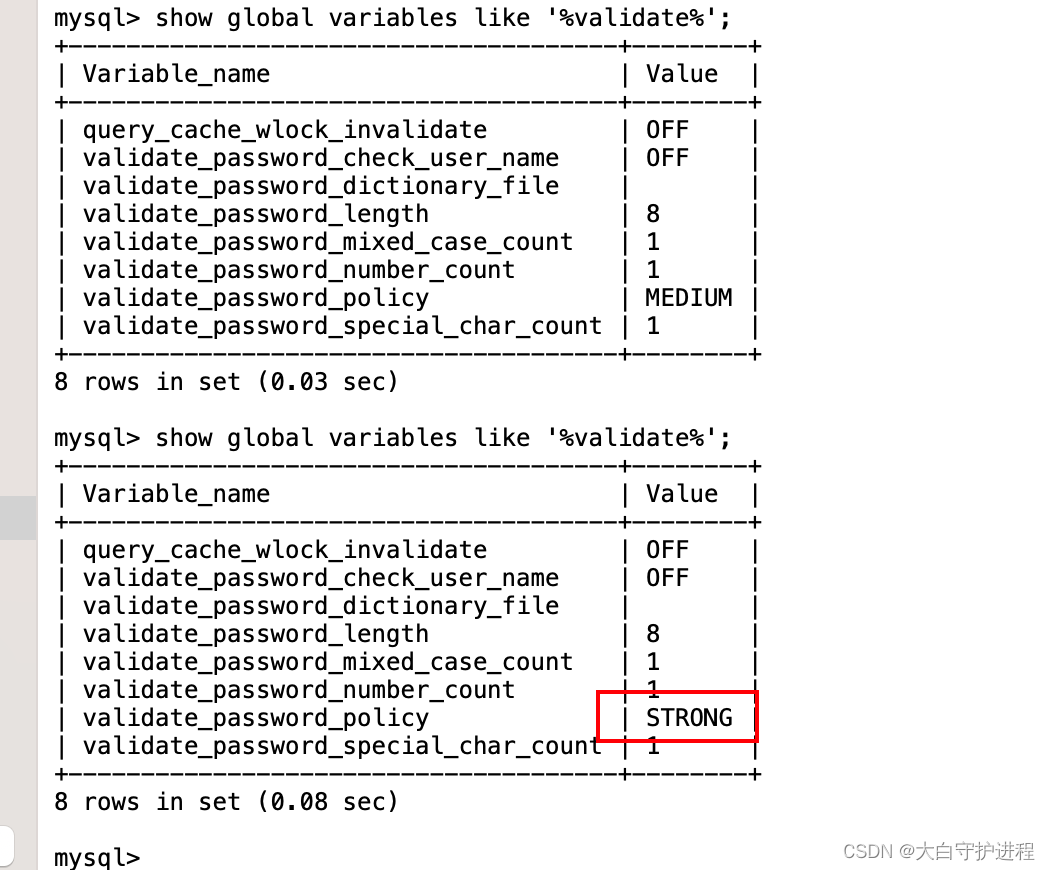
MySQL安装validate_password_policy插件
功能介绍 validate_password_policy 是插件用于验证密码强度的策略。该参数可以设定三种级别:0代表低,1代表中,2代表高。 validate_password_policy 主要影响密码的强度检查级别: 0/LOW:只检查密码长度。 1/MEDIUM&am…...

数据在内存中的存储——练习3
题目: 3.1 #include <stdio.h> int main() {char a -128;printf("%u\n",a);return 0; }3.2 #include <stdio.h> int main() {char a 128;printf("%u\n",a);return 0; }思路分析: 首先二者极其相似%u是无符号格式进行…...

web-案例
分页插件 登录 事务...
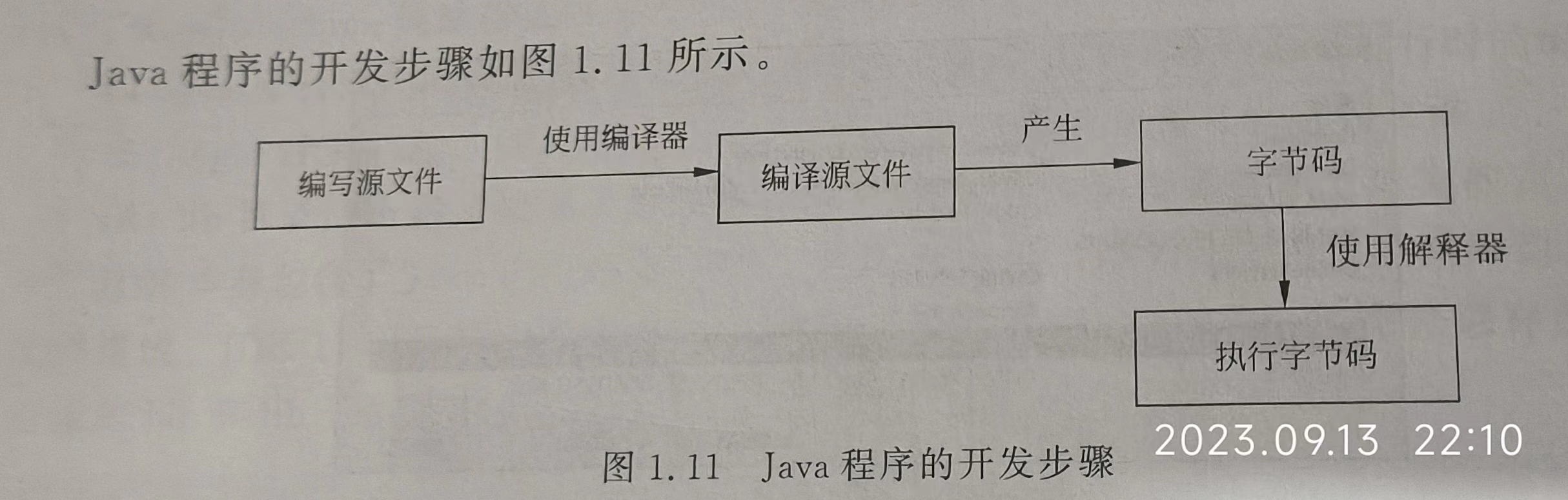
第一章 JAVA入门
文章目录 1.2 Java 的特点1.2.1 简单1.2.2 面向对象1.2.3 与平台无关① 平台与机器指令② C/C程序依赖平台③ Java 虚拟机与字节码1.2.4 多线程1.2.5 动态1.30安装 JDK1.3.1 平台简介0 Java SE②Java EE1.4 Java 程序的开发步骤②保存源文件1.5.2 编译1.8 Java之父-James Gosli…...
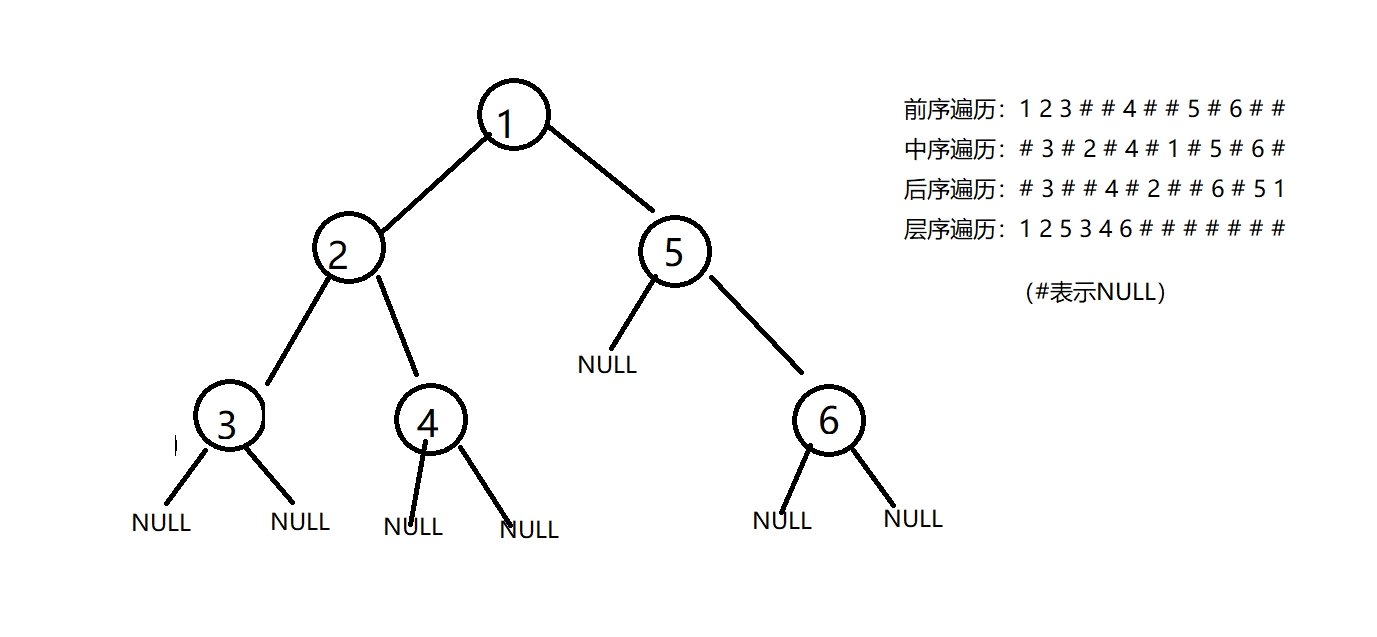
二叉树详解(求二叉树的结点个数、深度、第k层的个数、遍历等)
二叉树,是一种特殊的树,特点是树的度小于等于2(树的度是整个树的结点的度的最大值),由于该特性,构建二叉树的结点只有三个成员,结点的值和指向结点左、右子树的指针。 typedef int DateType; t…...

Apollo配置中心及Python连接
本文将会介绍如何启动Apollo,在Apollo中配置参数,以及如何使用Python连接Apollo. Apollo介绍 在文章Python之读取配置文件和文章Python之配置文件处理中,笔者分别介绍了如何使用Python来处理ini, yaml, conf等配置文件。这种配置方式比较方便…...
--audio - 多媒体音频)
LuatOS-SOC接口文档(air780E)--audio - 多媒体音频
常量 常量 类型 解释 audio.PCM number PCM格式,即原始ADC数据 audio.MORE_DATA number audio.on回调函数传入参数的值,表示底层播放完一段数据,可以传入更多数据 audio.DONE number audio.on回调函数传入参数的值,表示…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...
