【AI】机器学习——感知机
文章目录
- 4.1 感知机基本概念
- 4.2 策略
- 4.2.1 数据集的线性可分性
- 4.2.2 学习策略
- 目标
- 损失函数的构造
- 关于距离的解释
- 4.3 算法
- 4.3.1 原始形式
- 损失函数的梯度下降法
- 4.3.2 PLA例题
- 4.3.3 算法收敛性
- 4.4 PLA对偶形式
- 4.4.1 原始PLA分析
- 4.4.2 PLA对偶形式
- 4.4.3 优点
4.1 感知机基本概念
解决二分类问题,属于 线性分类模型——判别模型
目标:求出将训练数据进行线性划分的分离超平面
基本思想:导入五分类的损失函数,利用梯度下降法对损失i函数极小化,求得感知机模型
输入: x ∈ X ⊆ R n x\in \mathcal{X}\subseteq R^n x∈X⊆Rn 表示实例的特征向量, y ∈ Y = { + 1 , − 1 } y\in \mathcal{Y}=\{+1, -1\} y∈Y={+1,−1}
输出: ω ^ , b ^ \hat{\omega},\hat{b} ω^,b^
模型——决策函数
f ( x ) = s i g n ( ω T x + b ) = { + 1 , ω T x > 0 − 1 , ω T x < 0 f(x)=sign(\omega^Tx+b)=\begin{cases} +1&,\omega^Tx> 0\\ -1&,\omega^Tx<0 \end{cases} f(x)=sign(ωTx+b)={+1−1,ωTx>0,ωTx<0
假设空间:定义在特征空间中的所有线性分类模型
{ f ∣ f ( x ) = ω T x + b } \{f\vert f(x)=\omega^Tx+b\} {f∣f(x)=ωTx+b}
几何理解: ω T x + b = 0 \omega^Tx+b=0 ωTx+b=0 在空间中为一个超平面 S S S , ω \omega ω 为法向量, b b b 为截距
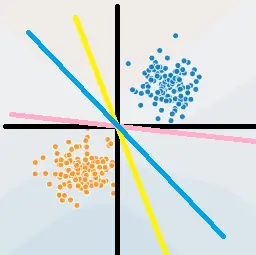
- 上图中超平面 S : ω 1 x ( 1 ) + ω 2 x ( 2 ) + b = 0 S:\omega_1x^{(1)}+\omega_2x^{(2)}+b=0 S:ω1x(1)+ω2x(2)+b=0 ,这个超平面将特征空间分为 + 1 , − 1 +1,-1 +1,−1 类
4.2 策略
损失函数的定义,并将 J ( ω ) J(\omega) J(ω) 最小化
4.2.1 数据集的线性可分性
对于数据集
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } x i ∈ X ⊆ R n , y i ∈ Y = { + 1 , − 1 } , i = 1 , 2 , ⋯ , N D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}\\ x_i\in \mathcal{X}\subseteq R^n,y_i\in\mathcal{Y}=\{+1,-1\},i=1,2,\cdots,N D={(x1,y1),(x2,y2),⋯,(xN,yN)}xi∈X⊆Rn,yi∈Y={+1,−1},i=1,2,⋯,N
若存在某个超平面 S S S : ω T x + b = 0 \omega^Tx+b=0 ωTx+b=0 ,将数据正负两类完全划分到超平面两侧
- 对于正例: y i = + 1 y_i=+1 yi=+1 ,有 ω T x + b > 0 \omega^Tx+b>0 ωTx+b>0
- 对于负例: y i = − 1 y_i=-1 yi=−1 ,有 ω T x + b < 0 \omega^Tx+b<0 ωTx+b<0
4.2.2 学习策略
目标
假设数据集D线性可分,找到将数据集D正负两例完全正确分开的超平面S,即确定参数 ω ^ , b ^ \hat{\omega},\hat{b} ω^,b^
损失函数的构造
可选择
- 误分类点的总数,但不关于 ω , b \omega,b ω,b 可导,是离散的
- 误分类点到超平面 S S S 的距离和
点 x i x_i xi 到平面 S S S 的总距离
ω T x i + b ∥ ω ∥ 2 \frac{\omega^Tx_i+b}{\Vert \omega\Vert_2} ∥ω∥2ωTxi+b
对于误分类点有 y i ⋅ ( ω T x i + b ) < 0 ⟺ − y i ⋅ ( ω T x i + b ) > 0 y_i\cdot(\omega^Tx_i+b)<0\iff -y_i\cdot(\omega^Tx_i+b)>0 yi⋅(ωTxi+b)<0⟺−yi⋅(ωTxi+b)>0
对于误分类点,到超平面的几何距离为
− 1 ∥ ω ∥ 2 y i ⋅ ( ω T x i + b ) -\frac{1}{\Vert \omega\Vert_2}y_i\cdot(\omega^Tx_i+b) −∥ω∥21yi⋅(ωTxi+b)
若所有误分类点集合为 M M M ,则误分类点到 S S S 的距离和为
− 1 ∥ ω ∥ 2 ∑ x i ∈ M y i ⋅ ( ω T x i + b ) -\frac{1}{\Vert \omega\Vert_2}\sum\limits_{x_i\in M}y_i\cdot(\omega^Tx_i+b) −∥ω∥21xi∈M∑yi⋅(ωTxi+b)
故将感知机(损失函数)定义为经验风险函数
R e m p ( f ) = L ( ω , b ) = − ∑ x i ∈ M y i ⋅ ( ω T x i + b ) R_{emp}(f)=L(\omega,b)=-\sum\limits_{x_i\in M}y_i\cdot(\omega^Tx_i+b) Remp(f)=L(ω,b)=−xi∈M∑yi⋅(ωTxi+b)
策略为 在假设空间中选取使损失函数 L ( ω , b ) L(\omega,b) L(ω,b) 最小的模型参数 ω , b \omega,b ω,b
- 损失函数非负
- 误分类点数量越少越好
- 误分类点离超平面越近越好
- L ( ω , b ) L(\omega,b) L(ω,b) 是连续可导的
关于距离的解释
− 1 ∥ ω ∥ 2 y i ⋅ ( ω T x i + b ) -\frac{1}{\Vert \omega\Vert_2}y_i\cdot(\omega^Tx_i+b) −∥ω∥21yi⋅(ωTxi+b) 为几何距离
− y i ⋅ ( ω T x i + b ) -y_i\cdot(\omega^Tx_i+b) −yi⋅(ωTxi+b) 为函数距离
几何距离的系数 1 ∥ ω ∥ 2 \frac{1}{\Vert \omega\Vert_2} ∥ω∥21 可以抵消系数同时放大的影响,如 a X + b Y + c = 0 aX+bY+c=0 aX+bY+c=0 与 2 a X + 2 b Y + 2 c = 0 2aX+2bY+2c=0 2aX+2bY+2c=0
- 但会增加梯度下降法计算的复杂度
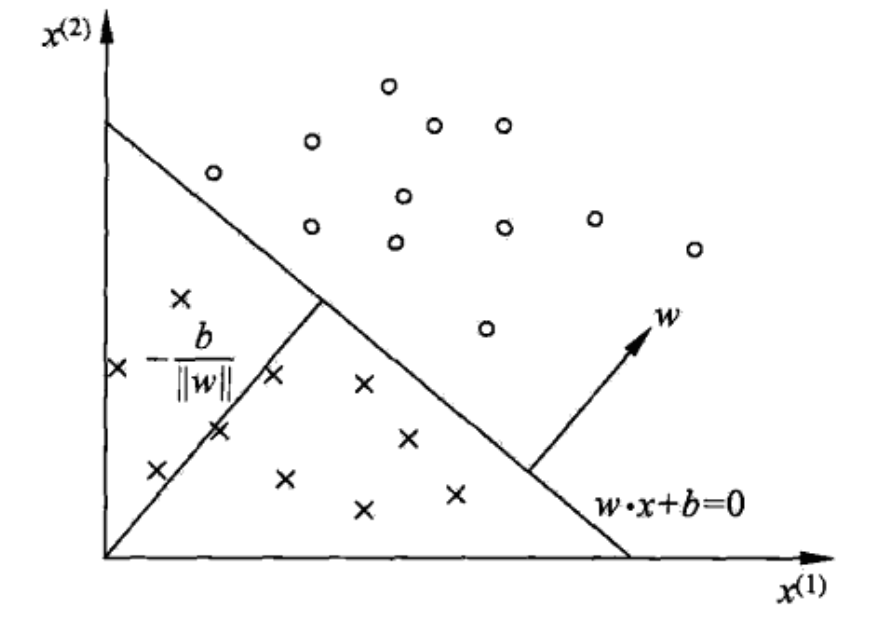
PLA的目标是使误分类点个数最小, 1 ∥ ω ∥ 2 \frac{1}{\Vert \omega\Vert_2} ∥ω∥21 对分类结果无影响
选取不同的初始 ω , b \omega,b ω,b ,最终会迭代出不同的超平面
4.3 算法
用随机梯度下降法,求解损失函数最优化问题
4.3.1 原始形式
输入:训练数据集
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } , x i ∈ X ⊆ R n , y i ∈ Y = { + 1 , − 1 } , i = 1 , 2 , ⋯ , N D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\},\\ x_i\in \mathcal{X}\subseteq R^n,y_i\in \mathcal{Y}=\{+1,-1\},i=1,2,\cdots,N D={(x1,y1),(x2,y2),⋯,(xN,yN)},xi∈X⊆Rn,yi∈Y={+1,−1},i=1,2,⋯,N
输出: ω ^ , b ^ \hat{\omega},\hat{b} ω^,b^
模型
f ( x ) = s i g n ( ω T x + b ) = { + 1 , ω T x + b > 0 − 1 , ω T x + b < 0 f(x)=sign(\omega^Tx+b)=\begin{cases} +1&,\omega^Tx+b>0\\ -1&,\omega^Tx+b<0\\ \end{cases} f(x)=sign(ωTx+b)={+1−1,ωTx+b>0,ωTx+b<0
策略
a r g min ω , b L ( ω , b ) = − ∑ x i ∈ M y i ⋅ ( ω T x i + b ) arg\min\limits_{\omega,b}L(\omega,b)=-\sum\limits_{x_i\in M}y_i\cdot(\omega^Tx_i+b) argω,bminL(ω,b)=−xi∈M∑yi⋅(ωTxi+b)
步骤
-
选取随机的 ω 0 , b 0 \omega_0,b_0 ω0,b0
-
在训练集中选数据 ( x i , y i ) (x_i,y_i) (xi,yi) ,将误分类点作为训练数据,即满足 ω T x i + b < 0 \omega^Tx_i+b<0 ωTxi+b<0 的条件的点
ω [ t + 1 ] ← ω [ t ] − η ∂ L ∂ ω = ω [ t ] + η y i x i b [ t + 1 ] ← b [ t ] − η ∂ L ∂ b = b [ t ] + η y i \omega^{[t+1]}\leftarrow\omega^{[t]}-\eta\frac{\partial L}{\partial \omega}=\omega^{[t]}+\eta y_ix_i\\ b^{[t+1]}\leftarrow b^{[t]}-\eta\frac{\partial L}{\partial b}=b^{[t]}+\eta y_i ω[t+1]←ω[t]−η∂ω∂L=ω[t]+ηyixib[t+1]←b[t]−η∂b∂L=b[t]+ηyi -
转至 2 2 2 步,直至 D D D 中无误分类点
损失函数的梯度下降法
{ ▽ ω L ( ω , b ) = − ∑ x i ∈ M y i x i ▽ b L ( ω , b ) = − ∑ x i ∈ M y i \begin{cases} \bigtriangledown_{\omega}L(\omega,b)=-\sum\limits_{x_i\in M}y_ix_i\\ \bigtriangledown_{b}L(\omega,b)=-\sum\limits_{x_i\in M}y_i\\ \end{cases} ⎩ ⎨ ⎧▽ωL(ω,b)=−xi∈M∑yixi▽bL(ω,b)=−xi∈M∑yi
前提是误分类点集合是固定的 ,才可进行梯度下降法最优化
{ ω ← ω − η ▽ ω L b ← b − η ▽ b L \begin{cases} \omega\leftarrow \omega-\eta\bigtriangledown_{\omega}L\\ b\leftarrow b-\eta\bigtriangledown_{b}L \end{cases} {ω←ω−η▽ωLb←b−η▽bL
这种做法:
- 计算量大
- 且调整参数 ω , b \omega,b ω,b 后,误分类点集可能会发生变化,故用随机梯度下降法
直观理解
当一个样本点被误分类时,调整 ω , b \omega,b ω,b 的值,使超平面 S S S 向该误分类点的一侧移动,减少该误分类点与 S S S 的距离,直至超平面越过此点(分类正确)
4.3.2 PLA例题
x 1 = ( 3 , 3 ) T , y 1 = + 1 x 2 = ( 4 , 3 ) T , y 2 = + 1 x 3 = ( 1 , 1 ) T , y 3 = − 1 x_1=(3,3)^T,y_1=+1\\ x_2=(4,3)^T,y_2=+1\\ x_3=(1,1)^T,y_3=-1\\ x1=(3,3)T,y1=+1x2=(4,3)T,y2=+1x3=(1,1)T,y3=−1
模型:
f ( x ) = s i g n ( ω T x + b ) = { + 1 , ω T x + b > 0 − 1 , ω T x + b < 0 ω = ( ω 1 ω 2 ) f(x)=sign(\omega^Tx+b)=\begin{cases} +1&,\omega^Tx+b>0\\ -1&,\omega^Tx+b<0 \end{cases}\\ \omega=\left( \begin{aligned} \omega_1\\ \omega_2 \end{aligned} \right) f(x)=sign(ωTx+b)={+1−1,ωTx+b>0,ωTx+b<0ω=(ω1ω2)
PLA策略为
min ω , b L ( ω , b ) = − ∑ x i ∈ M y i ( ω T ⋅ x + b ) \min\limits_{\omega,b}L(\omega,b)=-\sum\limits_{x_i\in M}y_i(\omega^T\cdot x+b) ω,bminL(ω,b)=−xi∈M∑yi(ωT⋅x+b)
算法:
-
取初值, ω 0 = ( 0 0 ) \omega_0=\left(\begin{aligned}0\\0\end{aligned}\right) ω0=(00) , b 0 = 0 b_0=0 b0=0 , η = 1 \eta=1 η=1
-
对 x 1 = ( 3 , 3 ) T x_1=(3,3)^T x1=(3,3)T ,有 y 1 ( ω 1 [ 0 ] x 1 ( 1 ) + ω 2 [ 0 ] x 1 ( 2 ) + b [ 0 ] ) = 0 y_1(\omega_1^{[0]}x_1^{(1)}+\omega_2^{[0]}x_1^{(2)}+b^{[0]})=0 y1(ω1[0]x1(1)+ω2[0]x1(2)+b[0])=0
未分类正确,故更新
{ ω [ 1 ] ← ω [ 0 ] − η ∂ L ∂ ω = ω [ 0 ] + η y i x i = ( 0 0 ) + ( 3 3 ) = ( 3 3 ) b [ 1 ] ← b [ 0 ] − η ∂ L ∂ b = b [ 0 ] + η y i = 0 + 1 ⋅ 1 = 1 \begin{cases} \omega^{[1]}\leftarrow\omega^{[0]}-\eta\frac{\partial L}{\partial \omega}=\omega^{[0]}+\eta y_ix_i= \left( \begin{aligned} 0\\0 \end{aligned} \right)+\left( \begin{aligned} 3\\3 \end{aligned} \right)=\left( \begin{aligned} 3\\3 \end{aligned} \right)\\ b^{[1]}\leftarrow b^{[0]}-\eta\frac{\partial L}{\partial b}=b^{[0]}+\eta y_i=0+1\cdot 1=1 \end{cases} ⎩ ⎨ ⎧ω[1]←ω[0]−η∂ω∂L=ω[0]+ηyixi=(00)+(33)=(33)b[1]←b[0]−η∂b∂L=b[0]+ηyi=0+1⋅1=1
故有线性模型
ω 1 T ⋅ x + b 1 = 3 x ( 1 ) + 3 x ( 2 ) + 1 \omega_1^{T}\cdot x+b_1=3x^{(1)}+3x^{(2)}+1 ω1T⋅x+b1=3x(1)+3x(2)+1 -
对 x 2 = ( 4 , 3 ) T , ( ω 1 [ 1 ] x 2 + ω 2 [ 1 ] x 2 + b [ 1 ] ) y 2 > 0 x_2=(4,3)^T,(\omega_1^{[1]}x_2+\omega_2^{[1]}x_2+b^{[1]})y_2>0 x2=(4,3)T,(ω1[1]x2+ω2[1]x2+b[1])y2>0 ,正确分类
x 3 = ( 1 , 1 ) T , ( ω 1 [ 1 ] x 3 + ω 2 [ 1 ] x 3 + b [ 1 ] ) y 3 < 0 x_3=(1,1)^T,(\omega_1^{[1]}x_3+\omega_2^{[1]}x_3+b^{[1]})y_3<0 x3=(1,1)T,(ω1[1]x3+ω2[1]x3+b[1])y3<0 ,误分类。用 ( x 3 , y 3 ) (x_3,y_3) (x3,y3) 更新模型参数
{ ω [ 2 ] ← ω [ 1 ] − η ∂ L ∂ ω = ω [ 1 ] + η y 3 x 3 = ( 3 3 ) + ( − 1 ) ( 1 1 ) = ( 2 2 ) b [ 1 ] ← b [ 0 ] − η ∂ L ∂ b = b [ 0 ] + η y 3 = 1 + 1 ⋅ ( − 1 ) = 0 \begin{cases} \omega^{[2]}\leftarrow\omega^{[1]}-\eta\frac{\partial L}{\partial \omega}=\omega^{[1]}+\eta y_3x_3= \left( \begin{aligned} 3\\3 \end{aligned} \right)+(-1)\left( \begin{aligned} 1\\1 \end{aligned} \right)=\left( \begin{aligned} 2\\2 \end{aligned} \right)\\ b^{[1]}\leftarrow b^{[0]}-\eta\frac{\partial L}{\partial b}=b^{[0]}+\eta y_3=1+1\cdot (-1)=0 \end{cases} ⎩ ⎨ ⎧ω[2]←ω[1]−η∂ω∂L=ω[1]+ηy3x3=(33)+(−1)(11)=(22)b[1]←b[0]−η∂b∂L=b[0]+ηy3=1+1⋅(−1)=0
有线性模型
ω 1 [ 2 ] x 1 + ω 2 [ 2 ] x 2 = 0 ⟺ 2 x 1 + 2 x 2 = 0 ⟺ x 1 + x 2 = 0 \omega^{[2]}_1x_1+\omega^{[2]}_2x_2=0\iff 2x_1+2x_2=0\iff x_1+x_2=0 ω1[2]x1+ω2[2]x2=0⟺2x1+2x2=0⟺x1+x2=0 -
对 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) (x_1,y_1),(x_2,y_2),(x_3,y_3) (x1,y1),(x2,y2),(x3,y3) 代入线性模型,反复迭代
直至无误分类样本点,有
ω [ 7 ] = ( 1 1 ) , b [ 7 ] = − 3 \omega^{[7]}=\left( \begin{aligned} 1\\1 \end{aligned} \right),b^{[7]}=-3 ω[7]=(11),b[7]=−3
超平面为 x ( 1 ) + x ( 2 ) − 3 = 0 x^{(1)}+x^{(2)}-3=0 x(1)+x(2)−3=0
4.3.3 算法收敛性
对于线性可分的训练数据集,经过有限次迭代(PLA可以在有限步终止) ,可以得到一个将训练数据集完全正确划分的超平面 S S S
定理
训练集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\} D={(x1,y1),(x2,y2),⋯,(xN,yN)} ,对于二分类模型, x i ∈ X ⊆ R n x_i\in \mathcal{X}\subseteq R^n xi∈X⊆Rn , y i ∈ Y = { + 1 , − 1 } y_i\in \mathcal{Y}=\{+1,-1\} yi∈Y={+1,−1} , i = 1 , 2 , ⋯ , N ,i=1,2,\cdots,N ,i=1,2,⋯,N
-
一定存在 ∥ ω ^ ∗ ∥ = 1 \Vert \hat{\omega}_*\Vert=1 ∥ω^∗∥=1 的超平面 ω ^ ∗ x T = 0 \hat{\omega}_*x^T=0 ω^∗xT=0 ,将数据完全正确划分,且存在 γ > 0 \gamma >0 γ>0 ,使
y i ( ω ^ ∗ x T ) ≥ γ ω ^ = ( ω ∗ b ∗ ) , x = ( x 1 ) y_i(\hat{\omega}_*x^T)\ge \gamma\\ \hat{\omega}=\left(\begin{aligned} \omega_*\\ b_* \end{aligned} \right),x=\left( \begin{aligned} x\\1 \end{aligned} \right) yi(ω^∗xT)≥γω^=(ω∗b∗),x=(x1)
证:由于线性可分,则可找到一个超平面 S : ω ^ ∗ x T = 0 S:\hat{\omega}_*x^T=0 S:ω^∗xT=0 ,使所有数据 y i ( ω ^ ∗ x T ) > 0 y_i(\hat{\omega}_*x^T)>0 yi(ω^∗xT)>0 分类正确可取 γ = min i { y i ( ω ^ ∗ x T ) } \gamma=\min\limits_{i}\{y_i(\hat{\omega}_*x^T)\} γ=imin{yi(ω^∗xT)} ,距离超平面最近的点
-
令 R = max 1 ≤ i ≤ N ∥ x i ∥ 2 R=\max\limits_{1\le i\le N}\Vert x_i\Vert_2 R=1≤i≤Nmax∥xi∥2 ,样本特征值最大的二范数 ,则PLA在训练数据集上误分类次数 k k k 满足 K ≤ ( R γ ) 2 K\le \left(\frac{R}{\gamma}\right)^2 K≤(γR)2
即离超平面越近的点越难分
感知机存在许多解,依赖于初值的选择
- 即误分类点的选择次序会影响最终的结果
4.4 PLA对偶形式
4.4.1 原始PLA分析
在原始 PLA 算法中, ω 0 , b 0 = 0 \omega_0,b_0=0 ω0,b0=0 , L ( ω , b ) = − ∑ x i ∈ M y i ( ω T ⋅ x + b ) L(\omega,b)=-\sum\limits_{x_i\in M}y_i(\omega^T\cdot x+b) L(ω,b)=−xi∈M∑yi(ωT⋅x+b) ,采用随机梯度下降算法,取一个误分类点 ( x i , y i ) (x_i,y_i) (xi,yi) 作为学习数据, η ∈ ( 0 , 1 ] \eta\in(0,1] η∈(0,1] 为学习率
{ ω [ t + 1 ] ← ω [ t ] − η ∂ L ∂ ω = ω [ t ] + η y i x i b [ t + 1 ] ← b [ t ] − η ∂ L ∂ b = b [ t ] + η y i \begin{cases} \omega^{[t+1]}\leftarrow\omega^{[t]}-\eta\frac{\partial L}{\partial \omega}=\omega^{[t]}+\eta y_ix_i\\ b^{[t+1]}\leftarrow b^{[t]}-\eta\frac{\partial L}{\partial b}=b^{[t]}+\eta y_i \end{cases} {ω[t+1]←ω[t]−η∂ω∂L=ω[t]+ηyixib[t+1]←b[t]−η∂b∂L=b[t]+ηyi
可见
-
ω \omega ω 更新至于误分类点有关
某个点使用次数越多,距超平面越近,越难正确分类
-
假设 ( x i , y i ) (x_i,y_i) (xi,yi) 被误分类 n i n_i ni 次,则 ω \omega ω 在 ( x i , y i ) (x_i,y_i) (xi,yi) 上的累积量为
{ ω i ← n i η y i x i = α i y i x i b i ← n i η y i = α i y i \begin{cases} \omega_i\leftarrow n_i\eta y_ix_i=\alpha_iy_ix_i\\ b_i\leftarrow n_i\eta y_i=\alpha_iy_i \end{cases} {ωi←niηyixi=αiyixibi←niηyi=αiyi
且对于正确分类的点 n i = 0 n_i=0 ni=0 ,故原始PLA参数可表示为
{ ω ← ∑ j = 1 N n j η y j ⋅ x j b ← ∑ j = 1 N n j η y j \begin{cases} \omega\leftarrow \sum\limits_{j=1}^Nn_j\eta y_j\cdot x_j\\ b\leftarrow \sum\limits_{j=1}^N n_j\eta y_j \end{cases} ⎩ ⎨ ⎧ω←j=1∑Nnjηyj⋅xjb←j=1∑Nnjηyj
4.4.2 PLA对偶形式
输入: D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } , x i ∈ X ⊆ R n , y i ∈ Y = { + 1 , − 1 } , i = 1 , 2 , ⋯ , N D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\},x_i\in \mathcal{X}\subseteq R^n,y_i\in \mathcal{Y}=\{+1,-1\},i=1,2,\cdots,N D={(x1,y1),(x2,y2),⋯,(xN,yN)},xi∈X⊆Rn,yi∈Y={+1,−1},i=1,2,⋯,N
η ∈ ( 0 , 1 ] \eta\in (0,1] η∈(0,1]
模型
f ( x ) = s i g n [ ( ∑ j = 1 N n j η y j ⋅ x j ) T ⋅ x + ∑ j = 1 N n j η y j ] = s i g n [ ∑ j = 1 N α j y j ( x j ⋅ x ) T + b ] \begin{aligned} f(x)&=sign[(\sum\limits_{j=1}^Nn_j\eta y_j\cdot x_j)^T\cdot x+\sum\limits_{j=1}^N n_j\eta y_j]\\ &=sign[\sum\limits_{j=1}^N\alpha_j y_j(x_j\cdot x)^T+b] \end{aligned} f(x)=sign[(j=1∑Nnjηyj⋅xj)T⋅x+j=1∑Nnjηyj]=sign[j=1∑Nαjyj(xj⋅x)T+b]
输出 : α , b \alpha,b α,b α = ( α 1 α 2 ⋮ α N ) \alpha=\left(\begin{aligned}\alpha_1\\\alpha_2\\\vdots\\\alpha_N\end{aligned}\right) α= α1α2⋮αN , α i = n i η \alpha_i=n_i\eta αi=niη , n i n_i ni 为 ( x i , y i ) (x_i,y_i) (xi,yi) 被误分类的次数
步骤
-
∀ n i = 0 \forall n_i=0 ∀ni=0 ,即 α = 0 , b = 0 \alpha=0,b=0 α=0,b=0
-
选取 ( x i , y i ) (x_i,y_i) (xi,yi) ,若 y i [ ∑ j = 1 N n j η y j ( x j T ⋅ x ) + ∑ j = 1 N n j η y j ] ≤ 0 y_i[\sum\limits_{j=1}^Nn_j\eta y_j(x_j^T\cdot x)+\sum\limits_{j=1}^N n_j\eta y_j]\le 0 yi[j=1∑Nnjηyj(xjT⋅x)+j=1∑Nnjηyj]≤0 ,则令
n [ t + 1 ] ← n [ t ] + 1 α [ t + 1 ] ← α [ t ] + η b [ t + 1 ] ← b [ t ] + η y i n^{[t+1]}\leftarrow n^{[t]}+1\\ \alpha^{[t+1]}\leftarrow \alpha^{[t]}+\eta\\ b^{[t+1]}\leftarrow b^{[t]}+\eta y_i n[t+1]←n[t]+1α[t+1]←α[t]+ηb[t+1]←b[t]+ηyi -
转至 2. 2. 2. 直至没有误分类点
由于样本点只以内积形式出现,可计算 Gram矩阵
G = [ x i ⋅ x j ] N × N = [ ( x 1 , x 1 ) ( x 1 , x 2 ) ⋯ ( x 1 , x N ) ( x 2 , x 1 ) ( x 2 , x 2 ) ⋯ ( x 2 , x N ) ⋮ ⋮ ⋱ ⋮ ( x N , x 1 ) ( x N , x 2 ) ⋯ ( x N , x N ) ] G=[x_i\cdot x_j]_{N\times N}=\left[\begin{matrix} (x_1,x_1)&(x_1,x_2)&\cdots&(x_1,x_N)\\ (x_2,x_1)&(x_2,x_2)&\cdots&(x_2,x_N)\\ \vdots&\vdots&\ddots&\vdots\\ (x_N,x_1)&(x_N,x_2)&\cdots&(x_N,x_N) \end{matrix} \right] G=[xi⋅xj]N×N= (x1,x1)(x2,x1)⋮(xN,x1)(x1,x2)(x2,x2)⋮(xN,x2)⋯⋯⋱⋯(x1,xN)(x2,xN)⋮(xN,xN)
4.4.3 优点
可预先计算存储 Gram 矩阵,提高计算速度
可通过 Gram 矩阵引入核函数,有 K ( x , z ) = ϕ ( x ) ⋅ ϕ ( z ) K(x,z)=\phi(x)\cdot \phi(z) K(x,z)=ϕ(x)⋅ϕ(z) ,可解决非线性分类问题
相关文章:

【AI】机器学习——感知机
文章目录 4.1 感知机基本概念4.2 策略4.2.1 数据集的线性可分性4.2.2 学习策略目标损失函数的构造关于距离的解释 4.3 算法4.3.1 原始形式损失函数的梯度下降法 4.3.2 PLA例题4.3.3 算法收敛性 4.4 PLA对偶形式4.4.1 原始PLA分析4.4.2 PLA对偶形式4.4.3 优点 4.1 感知机基本概念…...

蓝牙遥控器在T2-U上的应用
文章目录 简介优势使用流程示例代码遥控器命令表遥控器代码实现开启遥控器配对功能运行 简介 Tuya beacon 协议是基于 BLE 广播通信技术,完善配对解绑、组包拆包、群组管理、加密解密、安全策略,形成的一种轻量、安全的可接入涂鸦云的蓝牙协议。 蓝牙 …...
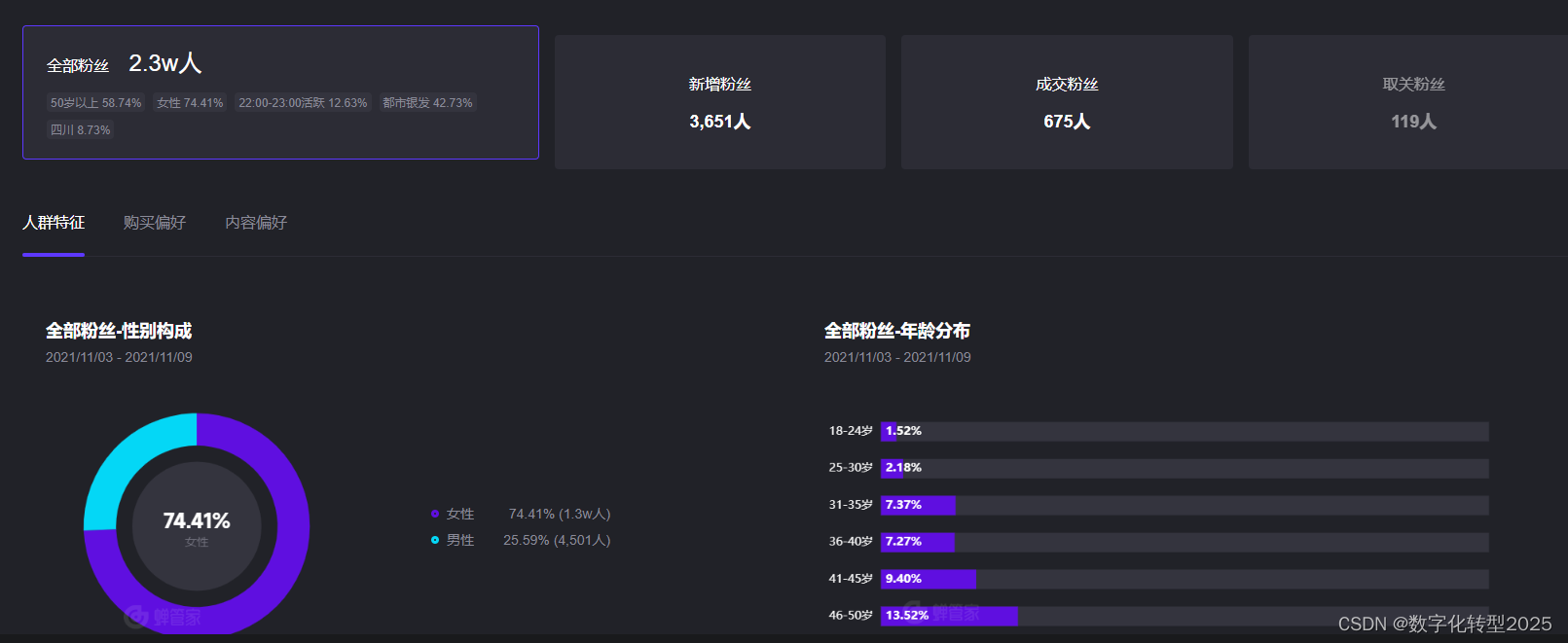
数据驱动的数字营销与消费者运营
引言:基于海洋馆文旅企业在推广宣传中,如何通过指标体系量化分析广告收益对业务带来的收益价值的思考? 第一部分:前链路引流投放的策略与实战 1.1 动态广告的实现: 偶然与必然 动态广告是一种基于实时数据和用户行为的广告形式,它…...

Qt点亮I.MX6U开发板的一个LED
本篇开始将会介绍与开发版相关的Qt项目,首先从点亮一个LED开始。I.MX6U和STM32MP157的相关信息都会用到,但是后期还是将I.MX6U的学习作为重点。当然其他开发版的开发也可以参考本博文。 文章目录 1. Qt是如何操控开发板上的一个LED2. 出厂内核设备树中注…...

网络摄像头-流媒体服务器-视频流客户端
取电脑的视频流 当涉及交通事件检测算法和摄像头视频数据处理时,涉及的代码案例可能会非常复杂,因为这涉及到多个组件和技术。以下是一个简单的Python代码示例,演示如何使用OpenCV库捕获摄像头视频流并进行实时车辆检测,这是一个…...
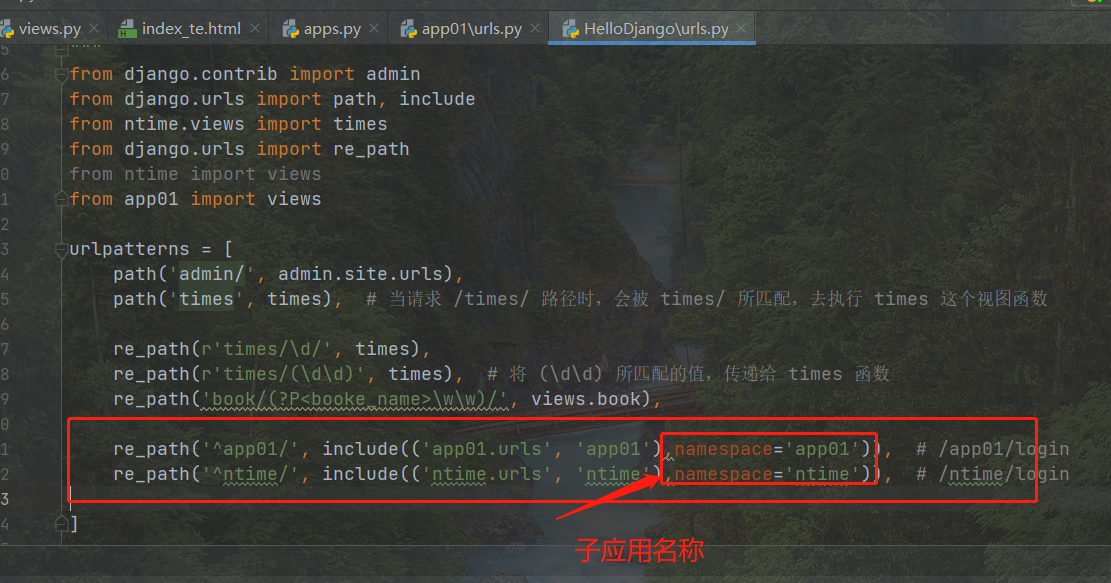
Django05_反向解析
Django05_反向解析 5.1 反向解析概述 随着功能的不断扩展,路由层的 url 发生变化,就需要去更改对应的视图层和模板层的 url,非常麻烦,不便维护。这个时候我们可以通过反向解析,将 url解析成对应的 试图函数 通过 path…...

基于HTML、CSS和JavaScript制作一个中秋节倒计时网页
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 这个项目使用HTML、CSS和…...

富斯I6刷10通道固件
使用USB转串口模块刷写10通道固件 一、下载固件 1. 十通道英文固件 下载地址: https://github.com/benb0jangles/FlySky-i6-Mod-/tree/master 选择 FlySky-i6-Mod–master \ 10ch Mod i6 Updater \ 10ch_MOD_i6_Programmer_V1 路径下的文件,亲测可用。 2. 原版六通道中…...

vector的模拟实现 总结
vector的模拟实现 总结 vector.hTest.cpp vector.h 1、迭代器的实现 #pragma oncenamespace JPC {template<class T>class vector{public://对于存储空间是连续的结构而言,可以用原身指针来 模拟实现 迭代器。typedef T* iterator;typedef const T* const_i…...

k8s中的有状态,无状态,pv、pvc等
数据库是一个典型的有状态服务,他的部署和无状态服务是不一样的。 PostgresSQL----基于Kubernetes部署PostgresSQL-CSDN博客 一、创建SC、PV和PVC存储对象 二、部署PostgresSQL Volume Kubernetes 中文指南——云原生应用架构实战手册 有状态应用: …...
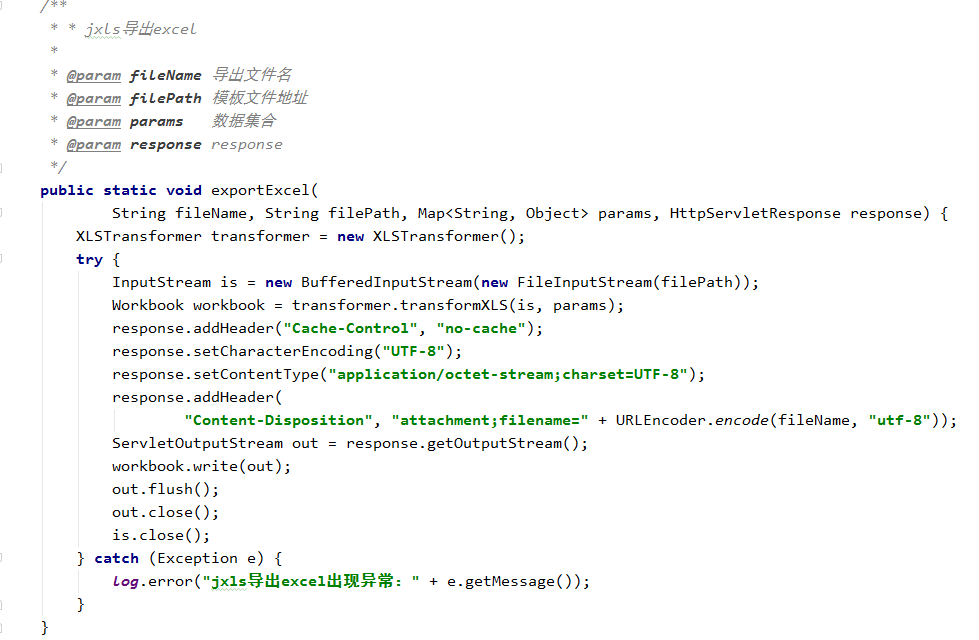
springboot+jxls复杂excel模板导出
JXLS 是基于 Jakarta POI API 的 Excel 报表生成工具,可以生成精美的 Excel 格式报表。它采用标签的方式,类似 JSP 标签,写一个 Excel 模板,然后生成报表,非常灵活,简单! Java 有一些用于创建 …...
用selenium webdriver获取网站cookie后,实现免登录上网站
以csdn为例,代码分为两部分。 一、csdn_get_cookies.py为半手动登录网站后获取cookies 二、csdn_use_cookies.py为使用获取到的cookies免登录上网站 #获取登录cookiesfrom selenium import webdriver import jsoncsdn_driver webdriver.Chrome() url "htt…...

如何使用Java进行安全测试?
要使用Java进行安全测试,可以按照以下步骤进行: 确定测试目标:首先,明确要测试的应用程序或系统的安全目标和需求。确定要测试的安全方面,如身份验证、授权、输入验证、安全配置等。 了解安全测试知识:熟悉…...
)
Linux之Socket函数(详细篇)
本篇是基于Linux man手册的一些总结 socket作用: create an endpoint for communication 函数结构 c #include <sys/types.h> /* See NOTES */ #include <sys/socket.h> int socket(int domain, int type, int protocol); 描述 socket() …...
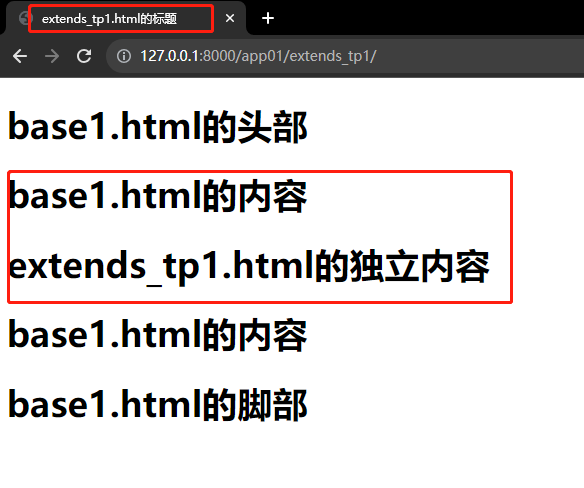
Dajngo06_Template模板
Dajngo06_Template模板 6.1 Template模板概述 模板引擎是一种可以让开发者把服务端数据填充到html网页中完成渲染效果的技术 静态网页:页面上的数据都是写死的,万年不变 动态网页:页面上的数据是从后端动态获取的(后端获取数据库…...
快速幂 c++
一般大家写都是 int ans 1; for (int i 1; i < a; i )ans * x;时间复杂度 但是这对于我们还不够,我们要 首先我们得知道一个数学知识 那么求 就有以下递归式 a 能被2整除 a 不能被2整除 (这里a/2是整除) 所以每次都调用 不就是么 最后补充一个东西…...

分享一个基于微信小程序的医院口腔助手小程序 牙科诊所预约小程序 源码 lw 调试
💕💕作者:计算机源码社 💕💕个人简介:本人七年开发经验,擅长Java、Python、PHP、.NET、微信小程序、爬虫、大数据等,大家有这一块的问题可以一起交流! 💕&…...
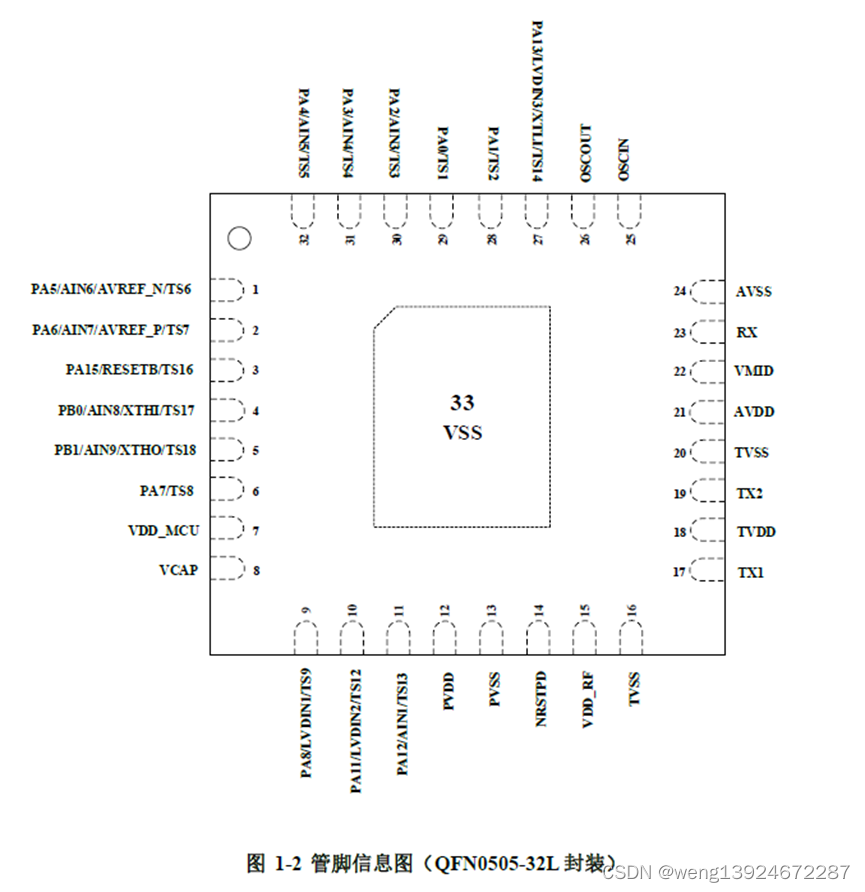
Si3262 一款低功耗刷卡+触摸+mcu 三合一SOC芯片
Si3262是-款高度集成的低功耗soC芯片,其集成了基于RISC-V 核的低功耗MCU和工作在13.56MHz的非接触式读写器模块。 该芯片ACD模式下刷卡距离可达4-5cm(天线决定),适用于智能门锁,电子锁,柜锁,桑拿…...

[H5动画制作系列] 奔跑的豹子的四种Demo演化
资源: bg.jpg: leopard.png: 背景透明 peopard2.png 背景不透明 参考代码1: leopard.js: (function(window) {ma function() {this.initialize();}ma._SpriteSheet new createjs.SpriteSheet({images: ["leopard.png"], frames: [[0,0,484,207],[486,0,484,207]…...

如何实现让一个函数能返回多个值的效果
在C语言中,一个函数通常只能返回一个值。但是可以通过指针参数或结构体来模拟返回多个值的效果。 使用指针参数:你可以将需要返回的值作为函数的参数,通过指针的形式传入,让函数将结果写入指针所指向的内存位置。 void multiple…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
